View - Universidad de Almería

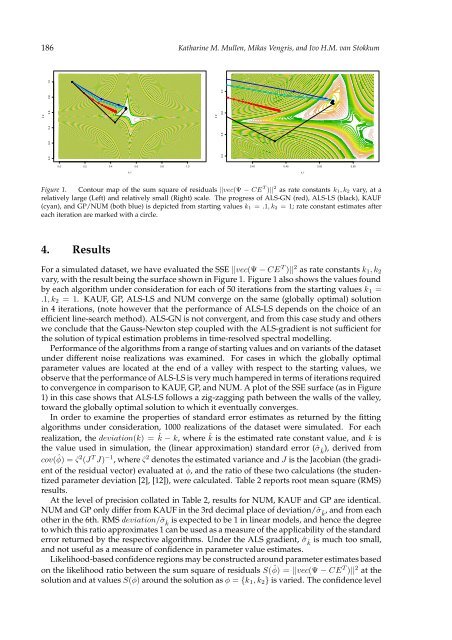
186 Katharine M. Mullen, Mikas Vengris, and Ivo H.M. van Stokkumk 20.0 0.2 0.4 0.6 0.8 1.0k 20.4 0.5 0.6 0.70.0 0.2 0.4 0.6 0.8 1.0k 10.40 0.45 0.50 0.55k 1Figure 1. Contour map of the sum square of residuals ||vec(Ψ − CE T )|| 2 as rate constants k 1, k 2 vary, at arelatively large (Left) and relatively small (Right) scale. The progress of ALS-GN (red), ALS-LS (black), KAUF(cyan), and GP/NUM (both blue) is depicted from starting values k 1 = .1, k 2 = 1; rate constant estimates aftereach iteration are marked with a circle.4. ResultsFor a simulated dataset, we have evaluated the SSE ||vec(Ψ − CE T )|| 2 as rate constants k 1 , k 2vary, with the result being the surface shown in Figure 1. Figure 1 also shows the values foundby each algorithm under consideration for each of 50 iterations from the starting values k 1 =.1, k 2 = 1. KAUF, GP, ALS-LS and NUM converge on the same (globally optimal) solutionin 4 iterations, (note however that the performance of ALS-LS depends on the choice of anefficient line-search method). ALS-GN is not convergent, and from this case study and otherswe conclude that the Gauss-Newton step coupled with the ALS-gradient is not sufficient forthe solution of typical estimation problems in time-resolved spectral modelling.Performance of the algorithms from a range of starting values and on variants of the datasetunder different noise realizations was examined. For cases in which the globally optimalparameter values are located at the end of a valley with respect to the starting values, weobserve that the performance of ALS-LS is very much hampered in terms of iterations requiredto convergence in comparison to KAUF, GP, and NUM. A plot of the SSE surface (as in Figure1) in this case shows that ALS-LS follows a zig-zagging path between the walls of the valley,toward the globally optimal solution to which it eventually converges.In order to examine the properties of standard error estimates as returned by the fittingalgorithms under consideration, 1000 realizations of the dataset were simulated. For eachrealization, the deviation(k) = ˆk − k, where ˆk is the estimated rate constant value, and k isthe value used in simulation, the (linear approximation) standard error (ˆσˆk), derived fromcov( ˆφ) = ˆς 2 (J T J) −1 , where ˆς 2 denotes the estimated variance and J is the Jacobian (the gradientof the residual vector) evaluated at ˆφ, and the ratio of these two calculations (the studentizedparameter deviation [2], [12]), were calculated. Table 2 reports root mean square (RMS)results.At the level of precision collated in Table 2, results for NUM, KAUF and GP are identical.NUM and GP only differ from KAUF in the 3rd decimal place of deviation/ˆσˆk, and from eachother in the 6th. RMS deviation/ˆσˆk is expected to be 1 in linear models, and hence the degreeto which this ratio approximates 1 can be used as a measure of the applicability of the standarderror returned by the respective algorithms. Under the ALS gradient, ˆσˆkis much too small,and not useful as a measure of confidence in parameter value estimates.Likelihood-based confidence regions may be constructed around parameter estimates basedon the likelihood ratio between the sum square of residuals S( ˆφ) = ||vec(Ψ − CE T )|| 2 at thesolution and at values S(φ) around the solution as φ = {k 1 , k 2 } is varied. The confidence level