View - Universidad de Almería

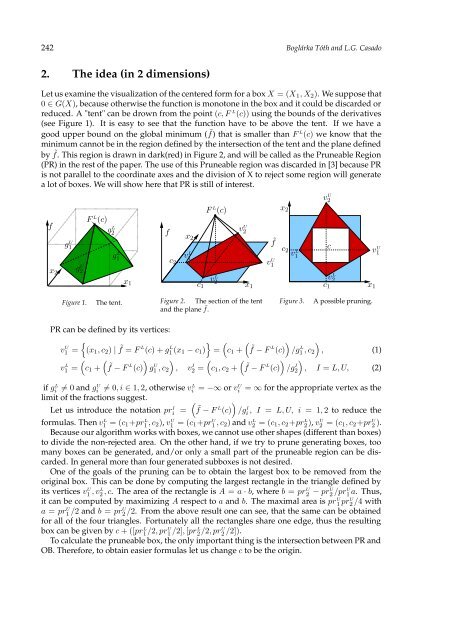
242 Boglárka Tóth and L.G. Casado2. The idea (in 2 dimensions)Let us examine PSfrag the visualization replacementsof the centered form for a box X = (X 1 , X 2 ). We suppose that0 ∈ G(X), because otherwise the function is monotone in the box and it could be discarded orreduced. A "tent" can be drown from the point (c, F L (c)) using the bounds of the derivatives(see Figure 1). It is easy to see that the function have to be above the tent. If we have agood upper bound on the global minimum ( ˜f) that is smaller than F L (c) we know that theminimum cannot be in the region defined by the intersection of the tent and the plane definedby ˜f. This region is drawn in dark(red) in Figure 2, and will be called as the Pruneable Regioneplacements (PR) in the rest of the paper. The use of this Pruneable region was discarded in [3] because PRis not parallel to the coordinate axes and the division PSfrag replacementsof X to reject some region will generatea lot of boxes. We will show here that PR is still of interest. F L (c)v U 2fx 2g U 1g U 2F L (c)g L 2g L 1x 1fx 2v1Lc 2c 1F L (c)v L 2v U 2x 1v U 1˜fx 2cc 2v1L v2Lc 1x 1v U 1Figure 1.The tent.Figure 2. The section of the tentand the plane ˜f.Figure 3.A possible pruning.PR can be defined by its vertices:v1 {(x U = 1 , c 2 ) | ˜f} ( ( )= F L (c) + g1 L (x 1 − c 1 ) = c 1 + ˜f − F L(c) /g1 L , c 2( ) )( )v1 (c L = 1 + ˜f − F L(c) g1 U , c 2 , v2 (c I = 1 , c 2 + ˜f − F L(c) /g2I), (1)), I = L, U, (2)if gi L ≠ 0 and gi U ≠ 0, i ∈ 1, 2, otherwise vi L = −∞ or vi U = ∞ for the appropriate vertex as thelimit of the fractions suggest.(Let us introduce the notation pr I i = ˜f − F L(c))/gi I , I = L, U, i = 1, 2 to reduce theformulas. Then v1 L = (c 1+pr L 1 , c 2), v1 U = (c 1+pr U 1 , c 2) and v2 L = (c 1, c 2 +pr L 2 ), vU 2 = (c 1, c 2 +pr U 2 ).Because our algorithm works with boxes, we cannot use other shapes (different than boxes)to divide the non-rejected area. On the other hand, if we try to prune generating boxes, toomany boxes can be generated, and/or only a small part of the pruneable region can be discarded.In general more than four generated subboxes is not desired.One of the goals of the pruning can be to obtain the largest box to be removed from theoriginal box. This can be done by computing the largest rectangle in the triangle defined byits vertices v1 U, vL 2 , c. The area of the rectangle is A = a · b, where b = prU 2 − prU 2 /prU 1 a. Thus,it can be computed by maximizing A respect to a and b. The maximal area is pr U 1 prU 2 /4 witha = pr U 1 /2 and b = prU 2 /2. From the above result one can see, that the same can be obtainedfor all of the four triangles. Fortunately all the rectangles share one edge, thus the resultingbox can be given by c + ([pr L 1 /2, prU 1 /2], [prL 2 /2, prU 2 /2]).To calculate the pruneable box, the only important thing is the intersection between PR andOB. Therefore, to obtain easier formulas let us change c to be the origin.