Electrons and Quantum Mechanics - Oakland Schools

4. Return the front target, carbon paper, marble, and paper clips to locations
designated by your teacher.
Data Analysis and Concept Development
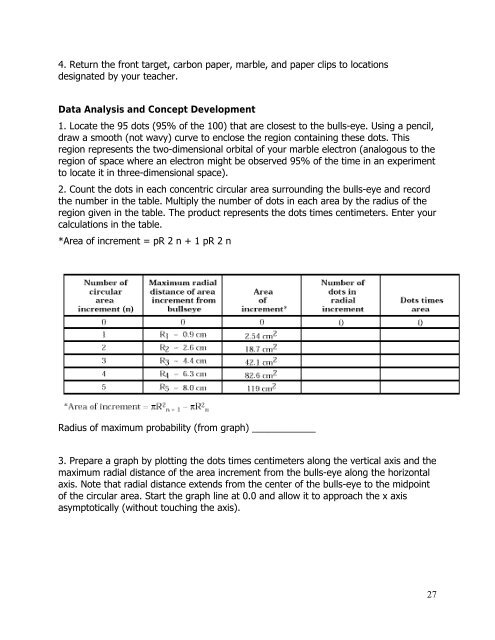
1. Locate the 95 dots (95% of the 100) that are closest to the bulls-eye. Using a pencil,
draw a smooth (not wavy) curve to enclose the region containing these dots. This
region represents the two-dimensional orbital of your marble electron (analogous to the
region of space where an electron might be observed 95% of the time in an experiment
to locate it in three-dimensional space).
2. Count the dots in each concentric circular area surrounding the bulls-eye and record
the number in the table. Multiply the number of dots in each area by the radius of the
region given in the table. The product represents the dots times centimeters. Enter your
calculations in the table.
*Area of increment = pR 2 n + 1 pR 2 n
Radius of maximum probability (from graph) ____________
3. Prepare a graph by plotting the dots times centimeters along the vertical axis and the
maximum radial distance of the area increment from the bulls-eye along the horizontal
axis. Note that radial distance extends from the center of the bulls-eye to the midpoint
of the circular area. Start the graph line at 0.0 and allow it to approach the x axis
asymptotically (without touching the axis).
27