RiskMetrics™ —Technical Document

52 Chapter 4. Statistical and probability foundations
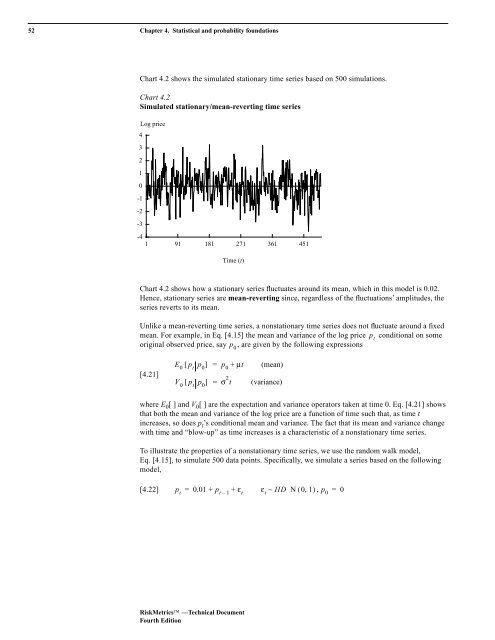
Chart 4.2 shows the simulated stationary time series based on 500 simulations.
Chart 4.2
Simulated stationary/mean-reverting time series
Log price
4
3
2
1
0
-1
-2
-3
-4
1 91 181 271 361 451
Time (t)
Chart 4.2 shows how a stationary series fluctuates around its mean, which in this model is 0.02.
Hence, stationary series are mean-reverting since, regardless of the fluctuations’ amplitudes, the
series reverts to its mean.
Unlike a mean-reverting time series, a nonstationary time series does not fluctuate around a fixed
mean. For example, in Eq. [4.15] the mean and variance of the log price p t
conditional on some
original observed price, say , are given by the following expressions
p 0
[4.21]
E 0
[ p t
p 0
] = p 0
+ µt (mean)
V 0
[ p t
p 0
] = σ 2 t (variance)
where E 0 [ ] and V 0 [ ] are the expectation and variance operators taken at time 0. Eq. [4.21] shows
that both the mean and variance of the log price are a function of time such that, as time t
increases, so does p t ’s conditional mean and variance. The fact that its mean and variance change
with time and “blow-up” as time increases is a characteristic of a nonstationary time series.
To illustrate the properties of a nonstationary time series, we use the random walk model,
Eq. [4.15], to simulate 500 data points. Specifically, we simulate a series based on the following
model,
[4.22]
p t
= 0.01 + p t – 1
+ ε t
ε t
∼ IID N ( 0,
1) , p 0
= 0
RiskMetrics —Technical Document
Fourth Edition