RiskMetrics™ —Technical Document

54 Chapter 4. Statistical and probability foundations
Notice how the 30-year rates fluctuate around the sample average of 7.30%, signifying that the
time series for this period is mean-reverting.
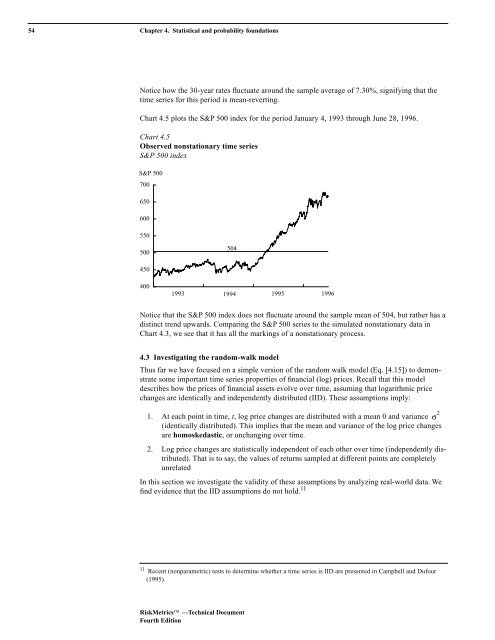
Chart 4.5 plots the S&P 500 index for the period January 4, 1993 through June 28, 1996.
Chart 4.5
Observed nonstationary time series
S&P 500 index
S&P 500
700
650
600
550
500
504
450
400
1993 1994 1995 1996
Notice that the S&P 500 index does not fluctuate around the sample mean of 504, but rather has a
distinct trend upwards. Comparing the S&P 500 series to the simulated nonstationary data in
Chart 4.3, we see that it has all the markings of a nonstationary process.
4.3 Investigating the random-walk model
Thus far we have focused on a simple version of the random walk model (Eq. [4.15]) to demonstrate
some important time series properties of financial (log) prices. Recall that this model
describes how the prices of financial assets evolve over time, assuming that logarithmic price
changes are identically and independently distributed (IID). These assumptions imply:
1. At each point in time, t, log price changes are distributed with a mean 0 and variance
(identically distributed). This implies that the mean and variance of the log price changes
are homoskedastic, or unchanging over time.
2. Log price changes are statistically independent of each other over time (independently distributed).
That is to say, the values of returns sampled at different points are completely
unrelated
In this section we investigate the validity of these assumptions by analyzing real-world data. We
find evidence that the IID assumptions do not hold. 11
σ 2
11 Recent (nonparametric) tests to determine whether a time series is IID are presented in Campbell and Dufour
(1995).
RiskMetrics —Technical Document
Fourth Edition