Spin-orbit coupling and electron-phonon scattering - Fachbereich ...

102 Coupled quantum dots in a phonon cavity
10
30
PSfrag replacements
20
qlb
0
qtb
10
0
i10
i10
0 10 20
0
10
q ‖ b
q ‖ b
20
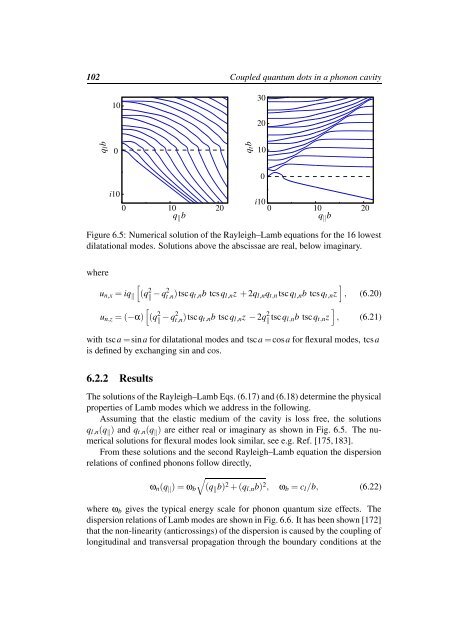
Figure 6.5: Numerical solution of the Rayleigh–Lamb equations for the 16 lowest
dilatational modes. Solutions above the abscissae are real, below imaginary.
where
u n,x = iq ‖
[(q 2 ‖ − q2 t.n)tscq t,n b tcsq l,n z + 2q l,n q t,n tscq l,n b tcsq t,n z
]
, (6.20)
[
]
u n,z = (−α) (q 2 ‖ − q2 t,n)tscq t,n b tscq l,n z − 2q 2 ‖ tscq l,nb tscq t,n z , (6.21)
with tsca =sina for dilatational modes and tsca =cosa for flexural modes, tcsa
is defined by exchanging sin and cos.
6.2.2 Results
The solutions of the Rayleigh–Lamb Eqs. (6.17) and (6.18) determine the physical
properties of Lamb modes which we address in the following.
Assuming that the elastic medium of the cavity is loss free, the solutions
q l,n (q ‖ ) and q t,n (q ‖ ) are either real or imaginary as shown in Fig. 6.5. The numerical
solutions for flexural modes look similar, see e.g. Ref. [175, 183].
From these solutions and the second Rayleigh–Lamb equation the dispersion
relations of confined phonons follow directly,
ω n (q ‖ ) = ω b
√(q ‖ b) 2 + (q l,n b) 2 , ω b = c l /b, (6.22)
where ω b gives the typical energy scale for phonon quantum size effects. The
dispersion relations of Lamb modes are shown in Fig. 6.6. It has been shown [172]
that the non-linearity (anticrossings) of the dispersion is caused by the coupling of
longitudinal and transversal propagation through the boundary conditions at the