Spin-orbit coupling and electron-phonon scattering - Fachbereich ...

# $
(
'
6.1 Control of dephasing and phonon emission in coupled quantum dots 93
"!
%$&
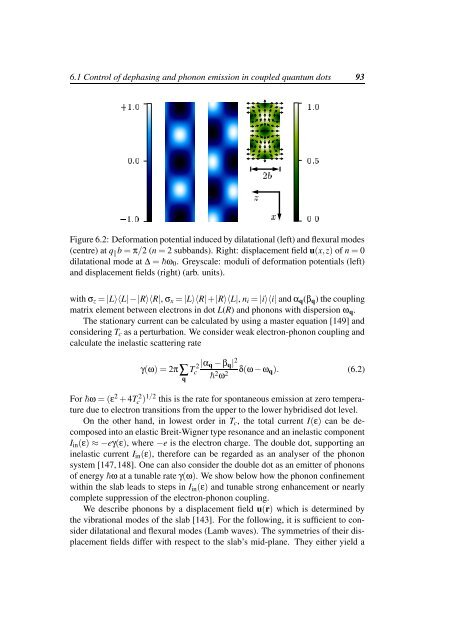
Figure 6.2: Deformation potential induced by dilatational (left) and flexural modes
(centre) at q ‖ b = π/2 (n = 2 subbands). Right: displacement field u(x,z) of n = 0
dilatational mode at ∆ = ω 0 . Greyscale: moduli of deformation potentials (left)
and displacement fields (right) (arb. units).
with σ z = |L〉〈L|−|R〉〈R|, σ x = |L〉〈R|+|R〉〈L|, n i = |i〉〈i| and α q (β q ) the coupling
matrix element between electrons in dot L(R) and phonons with dispersion ω q .
The stationary current can be calculated by using a master equation [149] and
considering T c as a perturbation. We consider weak electron-phonon coupling and
calculate the inelastic scattering rate
γ(ω) = 2π∑
q
Tc
2 |α q − β q | 2
2 ω 2 δ(ω − ω q ). (6.2)
For ω = (ε 2 + 4T 2
c ) 1/2 this is the rate for spontaneous emission at zero temperature
due to electron transitions from the upper to the lower hybridised dot level.
On the other hand, in lowest order in T c , the total current I(ε) can be decomposed
into an elastic Breit-Wigner type resonance and an inelastic component
I in (ε) ≈ −eγ(ε), where −e is the electron charge. The double dot, supporting an
inelastic current I in (ε), therefore can be regarded as an analyser of the phonon
system [147, 148]. One can also consider the double dot as an emitter of phonons
of energy ω at a tunable rate γ(ω). We show below how the phonon confinement
within the slab leads to steps in I in (ε) and tunable strong enhancement or nearly
complete suppression of the electron-phonon coupling.
We describe phonons by a displacement field u(r) which is determined by
the vibrational modes of the slab [143]. For the following, it is sufficient to consider
dilatational and flexural modes (Lamb waves). The symmetries of their displacement
fields differ with respect to the slab’s mid-plane. They either yield a