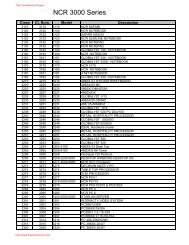
Synergy User Manual and Tutorial. - THE CORE MEMORY
Synergy User Manual and Tutorial. - THE CORE MEMORY
Synergy User Manual and Tutorial. - THE CORE MEMORY
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>Synergy</strong> <strong>User</strong> <strong>Manual</strong> <strong>and</strong> <strong>Tutorial</strong><br />
lxi<br />
Temporal Logic<br />
P<br />
F<br />
H<br />
G<br />
"It has at some time been the case that …"<br />
"It will at some time be the case that …"<br />
"It has always been the case that …"<br />
"It will always be the case that …"<br />
Pp ≡ ¬H¬p<br />
Fp ≡ ¬G¬p<br />
Gp→Fp<br />
"What will always be, will be"<br />
G(p→q)→(Gp→Gq) "If p will always imply q, then if p will always be the case, so will q"<br />
Fp→FFp<br />
"If it will be the case that p, it will be — in between — that it will be"<br />
¬Fp→F¬Fp "If it will never be that p then it will be that it will never be that p"<br />
p→HFp<br />
p→GPp<br />
H(p→q)→(Hp→Hq)<br />
G(p→q)→(Gp→Gq)<br />
"What is, has always been going to be"<br />
"What is, will always have been"<br />
"Whatever always follows from what always has been, always has been"<br />
"Whatever always follows from what always will be, always will be"<br />
RH: From a proof of p, derive a proof of Hp<br />
RG: From a proof of p, derive a proof of Gp<br />
F∃xp(x)→∃xFp(x)<br />
p")<br />
("If there will be something that is p, then there is now something that will be<br />
98