nøt_199504
nøt_199504
nøt_199504
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
260<br />
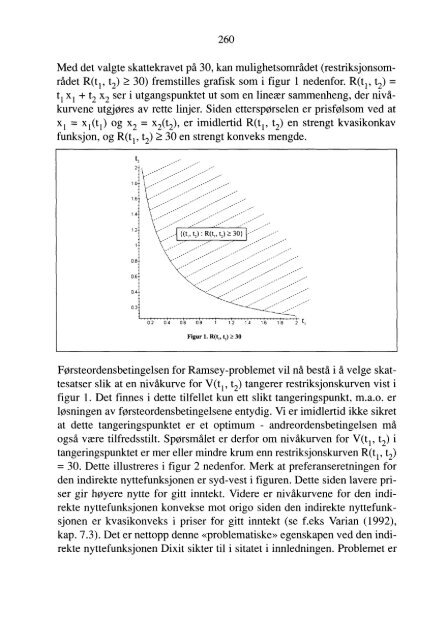
Med det valgte skattekravet på 30, kan mulighetsområdet (restriksjonsområdet<br />
R(t i , t2) 30) fremstilles grafisk som i figur 1 nedenfor. R(t i , t2) =<br />
t 1 x 1 + t2 x2 ser i utgangspunktet ut som en lineær sammenheng, der nivåkurvene<br />
utgjøres av rette linjer. Siden etterspørselen er prisfølsom ved at<br />
x 1 = x i (t i) og x2 = x2(t2), er imidlertid R(t i , t2) en strengt kvasikonkav<br />
funksjon, og R(t i , t2) 30 en strengt konveks mengde.<br />
Førsteordensbetingelsen for Ramsey-problemet vil nå bestå i å velge skattesatser<br />
slik at en nivåkurve for V(t i , t2) tangerer restriksjonskurven vist i<br />
figur 1. Det finnes i dette tilfellet kun ett slikt tangeringspunkt, m.a.o. er<br />
løsningen av førsteordensbetingelsene entydig. Vi er imidlertid ikke sikret<br />
at dette tangeringspunktet er et optimum - andreordensbetingelsen må<br />
også være tilfredsstilt. Spørsmålet er derfor om nivåkurven for V(ti , t2) i<br />
tangeringspunktet er mer eller mindre krum enn restriksjonskurven R(t i , t2)<br />
= 30. Dette illustreres i figur 2 nedenfor. Merk at preferanseretningen for<br />
den indirekte nyttefunksjonen er syd-vest i figuren. Dette siden lavere priser<br />
gir høyere nytte for gitt inntekt. Videre er nivåkurvene for den indirekte<br />
nyttefunksjonen konvekse mot origo siden den indirekte nyttefunksjonen<br />
er kvasikonveks i priser for gitt inntekt (se f.eks Varian (1992),<br />
kap. 7.3). Det er nettopp denne «problematiske» egenskapen ved den indirekte<br />
nyttefunksjonen Dixit sikter til i sitatet i innledningen. Problemet er