aspectos básicos para a quantização canônica de campos ...

AgradecimentosGostaria de deixar registrado neste trabalho o meu amplo agradecimento às pessoas que, dealguma forma, contribuíram e/ou contribuem para minha formação profissional e/ou pessoal.Pessoas essas que já faziam ou passaram a fazer parte de minha história e que terão minhahumilde e eterna gratidão.• É impossível se falar de física no Estado do Pará, sem que mencionemos o nome “JoséMaria Filardo Bassalo”. A este professor deixo um enorme agradecimento por ter sidoum dos pioneiros na tentativa de melhoria do curso ao qual dediquei parte destes últimosquatro anos de minha e por consegui sensibilizar uma geração de profissionais que seguemseu empenho, fazendo do curso de física um curso muito melhor do foi a pouco tempo atrás.A estes profissionais, que carregam arduamente o curso de Física em suas costas, deixoregistrada minha admiração e gratidão, neste aspecto, agradeço a vocês: Prof. Dr. LuísCarlos Bassalo Crispino, Prof. Dr. Sérgio Vizeu, Prof. Dr. Marcelo Lima, Prof. Dr. VanSérgio, Prof. Dr. Danilo Teixeira, Prof. Dra. Silvana Peres, Prof. Dra. Ângela Klautau,Prof. Dr. Sancleiton, Prof. Dr. Petrus Alcântara, Prof. Dr. Jorge Castiñeireas, Prof.Dr. Elinei e Prof. Dr. João Felipe. Neste momento corro o grande risco de ser injustocom alguém que, por ventura, esqueci de mencionar, porém mesmo numa Faculdade demais de 40 professores, tenho a triste certeza de que os possíveis injustiçados são umapequena parcela deste corpo docente, à essa minoria também registro minha gratidão eadmiração.• Agradeço ao Prof. Dr. Marcelo Lima por sua BOA VONTADE como professor, fatoeste que torna acessível a todos seus alunos uma grande fonte de conhecimento, o que,dentre outros motivos, o fazem ser um exemplo de profissional a ser seguido. Agradeço-lhetambém por algumas pequenas conversas e por seus longos discursos (em sala de aula efora dela) que, sem dúvida, foram de muita importância para minha formação.• Pelos bons e maus momentos que muito me ensinaram e pela rica convivência, maisii

quais não poderia ter feito nenhum dos agradecimentos anteriores. À estas pessoas, quevestem a camisa de pais como ninguém, registro minha eterna admiração e meu muitíssimoobrigado.iv

DedicatóriaAos meus pais:José Fernando e Maria do Socorro.E ao meu irmão:Fernando Bruno.v

ResumoNeste trabalho, faremos um estudo acerca do procedimento de quatização de campos escalarese vetoriais, abordando para isso não apenas o formalismo matemático envolvido no processo,mas também alguns importantes conceitos presentes na teoria. Começaremos pela quantizaçãoda corda, o que nos remete quase que de maneira imediata à quantização de campos escalaresmassivos, passando pelo campo eletromagnético e terminando com a quantização do campo deProca, calculando também seus respectivos propagadores de Feynman.vi

AbstractIn this work, we going to make a study of the quantization of scalar and vectorial field, using toit not only the math formalism, but also any important concepts of the theory. First we goingto do quatization the string, that remit to scalar massive field quantization, passing by photonfield and finishing with Proca field, computing also yours respective Feynman’s propagator.vii

ConteúdoAgradecimentos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iiDedicatória . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ivResumo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vAbstract . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . viiIntrodução 11 A Quantização da Corda 41.1 O Formalismo Lagrangeano para Campos Clássicos . . . . . . . . . . . . . . . . 41.2 A Quantização da Corda Não-Relativística . . . . . . . . . . . . . . . . . . . . . 91.2.1 Modos Normais da Corda . . . . . . . . . . . . . . . . . . . . . . . . . . 91.2.2 Aspectos Gerais para a Quantização de Campos e a Quantização da Corda 162 A Quantização de Campos Escalares 192.1 A Equação de Klein-Gordon . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192.2 A Quantização do Campo Escalar sujeito à Condições de Contorno Periódicas . 212.2.1 O Operador Hamiltoniano . . . . . . . . . . . . . . . . . . . . . . . . . . 222.3 A Quantização do Campo Escalar Livre . . . . . . . . . . . . . . . . . . . . . . . 333 A Quantização do Campo Eletromagnético 383.1 O Campo de Maxwell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 383.2 A Quantização do Campo Eletromagnético via Calibre de Coulomb . . . . . . . 403.3 A Quantização do Campo Eletromagnético via Calibre de Lorentz . . . . . . . . 453.4 O Calibre de Lorentz e o Método de Gupta-Bleuler . . . . . . . . . . . . . . . . 484 A Quantização do Campo Vetorial Massivo 554.1 As Equações de Proca . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 554.2 A Quantização do Campo de Proca . . . . . . . . . . . . . . . . . . . . . . . . . 57viii

5 O Propagador de Feynman 655.1 O Propagador do Campo Escalar Massivo . . . . . . . . . . . . . . . . . . . . . 655.2 O Propagador do Fóton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 695.3 O Propagador do Campo de Proca . . . . . . . . . . . . . . . . . . . . . . . . . 70Conclusão 78A O Eletromagnetismo de Maxwell 80B Os Vetores de Polarização 89C Propriedades Matemáticas da Função de Pauli-Jordan 92Referências 95ix

IntroduçãoUm dos maiores saltos da ciência em direção a uma melhor compreensão dos fenômenosnaturais foi a construção e a compreensão, no final do século XIX e início do século XX, deduas revolucionárias e polêmicas teorias: A Relatividade Restrita e a Mecânica Quântica. Taisteorias descrevem, respectivamente, sistemas que envolvem grandes velocidades, próximas avelocidade luz, e sistemas que envolvem estrutras muito pequenas, da ordem da constante dePlanck. Porém, os “mundos” descritos por essas teorias foram considerados separadamente,nos primórdios de suas construções. Então, como fica a descrição física da natureza que envolvequantidades muito pequenas que se deslocam em altas velocidades?Numa tentativa de responder a esta pergunta, surgiu, dentre outras, a Equação de Klein-Gordon. Tal equação não foi totalmente satisfatória para a descrição de partículas relativísticaspor apresentar inconsistências conceituais à luz da Teoria Quântica. Devido a isso esta equaçãofoi, de certa forma, abandonada para a descrição do mundo Quântico-Relativístico até o momentoem que a solução desta equação foi interpretada como um campo associado à partícula, enão como uma função de onda à esta. Surgiu assim, juntamente com o trabalho de Dirac na tentativade promover uma descrição relativística para o eletron, a chamada Teoria Quântica deCampos, conhecida também como Processo de Segunda Quantização que, diferentementedo procedimento de primeira quantização, ou quantização clássica, na qual as quantidades quantizadaseram as variáveis dinâmicas. Aqui levou-se em consideração a quantização dos próprioscampos responsáveis pela interação, sendo estes as variáveis dinâmicas a serem quantizadas.Assim a equação de Klein-Gordon passa a descrever campos cujas partículas associadas a estessão ditas Bosônicas, com spin 0. O desenvolvimento desta teoria fez com que esta se tornassecapaz de descrever outros tipos de campos, como, por exemplo, o Campo Vetorial, de spin1, levando em consideração, ou não, o elemento de massa associada cada um destes campos,ou partículas se preferir. Uma descrição mais detalhada de alguns dos campos mensionadosanteriormente será alvo desta monografia.Começaremos, logo no capítulo 1, apresentando o formalismo Lagrangeano para campos1

clássicos, mostrando que este pode ser entendido como um sistema de infinitas partículas muitopróximas. Após feito isso buscaremos a solução geral que descreve a corda vibrante e a quantizaremoslogo após de apresentarmos ao leitor o princípio da correspondência.No capítilo 2, apresentaremos a quantização do campo escalar real, cuja dinâmica é regidapela equação de Klein-Gordon. Este campo será quantizado sujeito a condições de contornoperiódicas, o que é muito similar à quantização da corda, e posteriormente será quantizadoquando livre no espaço.No capítulo 3, que terá como alvo a quantização do campo eletromagnético, começaremosapresentando o campo de Maxwell, posteriormente quantizaremos este levendo em consideraçãoduas importantes escolhas de calibres: o calibre de Coulomb e o calibre de Lorentz. Sendo queeste último deve, indiscutivelmente, levar em consideração a covariância do espaço-tempo, oque nos remete a considerar uma densidade de Lagrangeana modificada, escrita em termos deum parâmetro ξ, como veremos.No capítulo 4 apresentaremos detalhadamente a quantização do campo vetorial massivo,também conhecido como Campo de Proca. Começaremos apresentando quem são as equaçõesque regem a dinâmica deste campo para, à posteriori, quantizarmos a solução destas. Mostraremosainda neste capítulo que para garantirmos que o processo de quantização do campode Proca seja um processo covariante é necessário escrevê-lo em termos da chamada função dePauli-Jordan. A partir disso, seremos capazes quantizar todos os campos já apresentados noscapítulos 2 e 3, levando em consideração não apenas um deslocamento espacial, mas tambémum deslocamento temporal, obtendo, assim, a quantização para operadores de campo e seusmomentos canonicamente conjugados, localizados em pontos arbitrários no espaço-tempo.Finalmente, no capítulo 5, apresentaremos e calcularemos os propagadores de Feynmanpara cada um dos campos já quantizados no corpo deste trabalho, o que nos fornecerá oselementos fundamentais para a interpretação quântica da teoria: a amplitude de probabilidadede destruirmos num determinado ponto do espaço-tempo, uma partícula criada num outroponto deste mesmo espaço-tempo.A título de completeza também dispomos ao leitor um conjuntos de três apêndices que julgamosindispensáveis para o perfeito entendimento do trabalho aqui apresentado. Nominalmenteestes apêndices são: O Eletromagnetismo de Maxwell, no qual discutiremos aspectos fundamentaisdessa teoria e sua representação covariante; Os Vetores de Polarização, no qual,como diz o nome, discutiremos alguns detalhes destes objetos e sua importância nos procedimentosmatemáticos necessários para a quantização de campos; e, por fim, Propriedades2

Matemáticas da Função de Pauli-Jordan, no qual esta importante função será discutida,ressaltando, novamente como o nome já indica, suas propriedades matemáticas e sua relevâncianos processos de quantização de campos.3

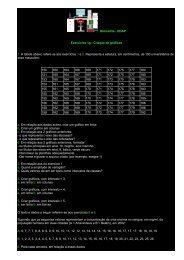
Capítulo 1A Quantização da CordaNeste capítulo mostraremos, basicamente, que a noção de campos clássicos pode emergirnaturalmente de sistemas de muitas partículas. Faremos ainda a quantização da corda nãorelativística,ou seja, na corda a qual viajam ondas com velocidade v muito mais baixa que avelocidade da luz. Mostraremos que a quantização da corda, em vários aspectos, é análoga àquantização de campos clássicos.Para tanto, antes de implementarmos tal quantização, nos é conveniente desenvolver ochamado formalismo Lagrangeano para campos clássicos, tomando, basicamente, o limite depassagem de sistemas discretos para sistemas contínuos.1.1 O Formalismo Lagrangeano para Campos ClássicosPara nossa finalidade nos é conveniente considerar um sistema mecânico composto por Nosciladores acoplados. Sendo m a massa de cada uma das partículas oscilantes, ligadas umasas outras por uma mola de constante elástica k, e que na posição de equilíbrio mantém umadistância a entre uma partícula e outra imediatamente sucessora ou antecessora à esta. Talsistema possui um comprimento fixo l (Figura 1.1).Figura 1.1: Osciladores acoplados.Podemos encontrar a Lagrangeana[20], também deste sistema, efetuando a diferençaL = T − V, (1.1)4

sendo T a energia cinética dada pore V a energia potencial dada porT = 1 2N∑i=12m i q˙i(1.2)V = 1 2N∑k(q i+1 − q i ) 2 . (1.3)i=1Logo, podemos reescrever a definição (1.1), de acordo com as definições para as energiascinéticas e potenciais dadas, respectivamente por (1.2) e (1.3), comoL = 1 2N∑[m i q˙2 i − k(q i+1 − q i ) 2 ]. (1.4)i=1Para encontrarmos as equações de movimento que regem este sistema basta que façamos asubstituição da equação (1.4) na Equação de Euler-Lagrange, dada por∂L∂q i− d dtCalculando cada termo da última equação, temos para o primeiro∂L∂q i= − 1 2N∑i=1( ) ∂L= 0. (1.5)∂q˙ik ∂∂q n(q i+1 − q i ) 2 ,que aplicando a derivada, segundo a regra da cadeia, fica∂L∂q i= −N∑i=1k(q i+1 − q i ) ∂∂q n(q i+1 − q i ).Note que ∂q i+1∂q n= δ n,i+1 e ainda ∂q i∂q n= δ n,i , assim∂L∂q i= −N∑k(q i+1 − q i )(δ n,i+1 − δ n,i ) (1.6)e ainda, para o segundo termo da equação de Euler-Lagrange, temosi=1∂L=∂q˙iN∑i=1m i q˙i δ n,i ,que, portanto, conforme o segundo termo da equação (1.5), vamos tomar sua derivada total notempo. Assim fazendo temos( )d ∂L=dt ∂q˙iN∑m i ¨q i δ n,i . (1.7)i=15

formaLogo, reunindo os resultados (1.6) e (1.7), temos que a equação de Euler-Lagrange ficará naN∑[k(q i+1 − q i )(δ n,i+1 − δ n,i ) − m i ¨q i δ n,i ] = 0.i=1Calculando o produto explicitado na equação acima e, após feito isso, utilizando a propriedadede filtragem da Delta, temos quem ¨q n + k(q n − q n+1 − q n−1 + q n ) = 0, (1.8)que é a equação de movimento para a N-ésima partícula do sistema.Para passarmos de um sistema discreto para um sistema contínuo, é necessário que façamossimultaneamente, o espaçamento entre as massas tender a zero, ou seja, a −→ 0, e o número departículas do sistema tender a infinito, ou seja, N −→ ∞, mantendo o comprimento l constante.E ainda, na somatória, fazerN∑−→ 1 ai=1sendo que, na última passagem, foi também necessária a introdução de um fator 1 para que osadois lados da igualdade sejam dimensionalmente consistentes. É, também, conveniente fazermosa seguinte parametrização na coordenada q n∫ l0dx,q n −→ √ aq(x), (1.9)sendo que x = na 1 e que √ a foi introduzida de maneira que garanta que nosso resultado nãoapresente divergências. Com isso podemos notar queq n+1 −→ √ aq(x + a). (1.10)Substituindo (1.9) e (1.10) na equação (1.8), teremos a equação de movimento não maisparametrizada em “n”, mas sim em “x”, na formam¨q(x) = k[q(x + a) − q(x) + q(x − a) − q(x)].Multiplicando e dividindo o segundo lado da igualdade por “a” e tomando o limite dea −→ 0, temos[ ]q(x + a) − q(x)m¨q(x) = ka lima−→0 a[ ]q(x − a) − q(x)+ ka lim. (1.11)a−→0 a1 Com esta nova definição para a variável “x” podemos parametrizar qualquer q n+m ; m = 0, 1, 2, 3..., logo:q n+m −→ √ aq[(n + m)a] = √ aq(x + ma)6

Em ambos os termos da última equação podemos identificar a própria definição de derivada,daí podemos reescrevê-la comom¨q(x) = ka[ ∂q(x)∂x | x+a − ∂q(x) ]∂x | x−a . (1.12)Repetindo o mesmo procedimento para a equação anterior, ou seja, multiplicando e dividindopor “a” o segundo lado da igualdade, identificamos mais uma vez a definição de derivadade forma que chegamos à relaçãom¨q(x) = ka 2 ∂2 q(x)∂x 2 , (1.13)envolvendo uma segunda derivada não apenas em “t” mas também em “x”.Identificando que a velocidade da onda que se propaga nessa corda é dada porv 2 = ka2m(1.14)e ressaltando que de fato q = q(x, t), teremos1v 2 ∂ 2 q(x, t)∂t 2 − ∂2 q(x, t)∂x 2 = 0, (1.15)da qual concluimos que o limite do contínuo para a equação (1.8) é a própria equação da onda.Com o propósito de reescrevermos a equação da onda de maneira compacta, definimos nessemomento o D’Lambertiano, dado por□ = 1 v 2 ∂ 2de maneira que a equação da onda pode ser reescrita como∂t 2 − ∂2∂x 2 , (1.16)□q(x, t) = 0. (1.17)Para a Lagrangeana dada pela equação (1.4), fazendo uso das relações (1.9) e (1.10), eindentificando definições de derivadas no último termo, teremos queL = 1 ∫ [l( ) 2 ( ) ] 2 ∂q ∂qm − ka 2 dx,2 ∂t ∂xde onde temos finalmente, usando (1.14),L = 1 ∫ [l( ) 21 ∂q−2 v 2 ∂t00( ) ] 2 ∂qdx, (1.18)∂x7

que é a Lagrangeana (1.4) escrita no limite do contínuo, ou seja, a Lagrangeana para a cordaclássica.Podemos notar na equação (1.18) que seu integrando pode ser identificado como uma Densidadede Lagrangeana, que por sua vez nos fornece a Lagrangeana quando a integramos emtodo espaço considerado, ou seja,L =∫ l0Ldx. (1.19)Logo, comparando as equações (1.18) e (1.19) e, fazendo, por conveniência, a substituiçãoq(x, t) −→ ϕ(x, t) obtemosL = 12v 2 ( ∂ϕ∂t) 2− 1 2que é a Densidade de Lagrangeana para a corda vibrante.( ) 2 ∂ϕ, (1.20)∂xDe forma que suas energias cinéticas e potenciais são, respectivamente, redefinidas comoeT = 12v 2 ∫ l0( ) 2 ∂ϕdx (1.21)∂tV = 1 2∫ l0( ) 2 ∂ϕdx. (1.22)∂xPara que a equação da onda dada por (1.15), na qual surge uma espécie de covariancia entreas coordenadas espacial e teporal, seja obtida diretamente da equação de Euler-Lagrange, estaúltima deve ser modificada de tal maneira que leve em consideração a covariamcia observada.Devido a isso a equação de Euler-Lagrange, já em sua forma modificada (covariante), vem aser∂L∂ϕ − ∂ ∂Lµ∂∂ µ ϕ= 0, (1.23)que é a equação de Euler-Lagrange para campos clássicos, onde os operadores ∂ µ nada maissão do que derivadas covariantes, em relação ao tempo e ao espaço. Como µ varia de 0 a 3,adotaremos ∂ 0 como uma derivada parcial no tempo, ou seja,∂ 0 = ∂ ∂t , (1.24)e ainda ∂ i , onde i = 1, 2, 3, como as derivadas parciais no espaço, ou seja,∂ 1 = ∂∂x , ∂ 2 = ∂ ∂y , ∂ 3 = ∂ ∂z . (1.25)8

De forma compacta esse operador pode também ser reescrito como∂ µ = (∂ 0 , ∂ i ). (1.26)A equação (1.23) também pode ser obtida através do Princípio Hamilton para camposclássicos, tal feito pode ser encontrado na referência[10] deste trabalho.Análogo ao tratamento da equação de Euler-Lagrange para sistemas discretos, onde o momentogeneralizado é dado porp qi = ∂L∂ ˙q i, (1.27)podemos ainda identificar uma importante relação que nos será muito útil, tal relação é dadaporπ =∂L∂∂ 0 ϕ , (1.28)considerando a densidade de Lagrangeana já encontrada anteriormente, reduzimos esta últimaequação aπ = 1 v 2 ∂ 0ϕ (1.29)que é o momento canonicamente conjugado ao campo ϕ, que descreve a corda vibrante.1.2 A Quantização da Corda Não-RelativísticaUma vez obtida a solução do problema para a corda vibrante por meio da passagem aocontínuo de um conjunto de osciladores acoplados é de suma importância apresentar um métodoconsistente de quantização.Aqui, ao fazermos a mudança q(x, t) para ϕ(x, t), introduzimos a idéia de que o comportamentoda corda, ou melhor ainda, o comportamento de cada ponto constituinte da corda,é dado pela função ϕ(x, t), que doravante chamaremos de campo, campo este, oscilante, queanteriormente foi representado pela corda vibrante.1.2.1 Modos Normais da CordaToda onda pode ser escrita como uma superposição de ondas planas[10], inclusive a ondaque se propaga numa corda descrita, como vimos, por ϕ(x, t), logo podemos dizer que∞∑ϕ(x, t) = c n e i(knx−wnt) , (1.30)n=−∞9

na qual cada valor de n está associado com cada modo normal de vibração da corda, sendo c na amplitude da onda devido a cada modo normal de oscilação. De acordo com as condições decontorno periódicas impostas sobre a corda, efetivadas por extremidades fixas e comprimentoL, podemos definirk n = nπ L , (1.31)como sendo o número de onda que. Para tal caso, temos ainda quew n = k n v, (1.32)conhecida como relação de dispersão, essencial para que a equação (1.30) seja de fato soluçãoda equação da onda, entendida também como a freqüência de oscilação da corda (ou campo).A equação (1.30) represeta, basicamente, uma série de Fourrier na forma exponencial[3] epode também ser escrita, reunindo todos os termos de dependência temporal em ϕ n (t), como∞∑ϕ(x, t) = ϕ n (t)e iknx , (1.33)assumindo quen=−∞ϕ n (t) = c n e −iwnt . (1.34)Multiplicando toda a equação anterior por e ik n ′ x e integrando em x, temos que∫ Lϕ(x, t)e −ik n ′ x dx =∞∑∫ L0n=−∞ 0Porém, usando a representação da Delta[10] dada por∫ Lobtemos queϕ n (t) = 1 L0ϕ n (t)e i(kn−k n ′ )x dx.e i(kn±k n ′ ) dx = Lδ n,∓n ′, (1.35)∫ L0ϕ(x, t)e −iknx dx. (1.36)Uma vez que a equação (1.33) é construída como uma superposição de ondas planas, elaobedece à equação da onda dada por (1.17), ou seja,□ϕ(x, t) = 0, (1.37)10

ou ainda, explicitamente( )1 ∂ 2v 2 ∂t − ∂22 ∂x 2∞∑n=−∞ϕ n (t)e iknx = 0,na qual, aplicando as derivadas teporais e espaciais temos∞∑n=−∞e usando (1.32), temos por fim[ ]1e iknx v ¨ϕ n(t) + k 2 2 n ϕ n (t) = 0,¨ϕ n (t) + w 2 nϕ n (t) = 0, (1.38)que é a equação típica do oscilador harmônico simples, cuja solução geral[20] é dada porϕ n (t) = a n e −iwnt + b n e iwnt , (1.39)sendo a n e b n constantes que podem ser determinadas a partir das condições iniciais do problemaem questão.Para que a solução dada pela equação (1.33) seja consistente com uma descrição física,devemos garantir que esta pertença ao conjunto dos reais fazendode onde segue, segundo (1.33), que∞∑n=−∞ϕ(x, t) = ϕ ∗ (x, t), (1.40)ϕ n (t)e iknx =∞∑n=−∞ϕ ∗ n(t)e −iknx .Substituindo n −→ −n no lado esquerdo da igualdade da última equação e invertendo o somatórioviráque também fará sentido se∞∑n=−∞o que nos leva a concluir queϕ −n (t)e ik −nx =∞∑n=−∞ϕ ∗ n(t)e −iknx ,k −n = −k n , (1.41)ϕ −n (t) = ϕ ∗ n(t). (1.42)11

Então a solução geral pode ser re-escrita, com base em (1.39), comoa −n e −iw−nt + b −n e iw−nt = a ∗ ne iwnt + b ∗ ne −iwnt . (1.43)Comparando os termos nos dois lados da igualdade, concluímos quew −n = w n (1.44)e ainda{a−n = b ∗ nb −n = a ∗ n.(1.45)Então, substituindo (1.39) na equação (1.33), temos que esta se dará na forma∞∑ϕ(x, t) = (a n e −iwnt + b n e iwnt )e iknx ,n=−∞ou ainda∞∑ϕ(x, t) = [a n e (iknx−iwnt) + b n e (iknx+iwnt) ].n=−∞A condição de realidade para a última equação nos leva, novamente, à troca n −→ −nno segundo termo da somatória. Fazendo isso e levando em conta as relações (1.41), (1.44) e(1.45), podemos re-escrever tal equação como∞∑ϕ(x, t) = [a n e (iknx−iwnt) + a ∗ ne (−iknx+iwnt) ]. (1.46)n=−∞Note na equação (1.46), solução clássica para o oscilador harmônico simples, que os termossomados são de tal forma que um é o complexo conjugado do outro, fato este que nos garantequalquer função (ou número) pertejnça ao conjunto dos números reais[20].Como o intuito deste capítulo é a quantização da equação (1.46), o primeiro passo neste caminhoé garantir que ela seja normalizável, de maneira a garantir a interpretação probabilística dafunção de onda. Para isso nos é conveniente definir uma solução dita ortonormalizável escritacomou n (x, t) = D n e −iwnt+iknx , (1.47)sendo D n uma constante de normalização que determinaremos a partir de então. Para essafunção, dada por (1.47), temos que a derivada temporal será dada por∂ 0 u n (x, t) = ˙u n (x, t) = −iw n u n (x, t), (1.48)12

e ainda a derivada espacial porque nos serão bastante úteis posteriormente.∂ x u n (x, t) = ik n u n (x, t), (1.49)Antes de proseguirmos com os cálculos para a determinação da constante D n propriamentedita nos é relevante calcular algumas integrais que nos serão de muita importância para essefeito. Vamos primeiramente obter as integrais de normalização para u n e u n ′, de maneira que∫ L0u n u n ′dx =∫ L0D n D n ′e −i(wn+w n ′)t+i(kn+k n ′)x dx∫ L= D n D n ′e −i(wn+w n ′)t e i(kn+k n ′ )x dx,que, de acordo com a representação da Delta dada por (1.35), a integral acima ficará∫ LCalculando também para u ∗ n e u ∗ n ′, temos∫ L000u n u n ′dx = LD n D n ′e −i(wn+w n ′ )t δ n,−n ′. (1.50)∫ Lu ∗ nu ∗ n ′dx = DnD ∗ n ∗ ′ei(wn+w n ′)t−i(kn+k n ′)x dx,e usando novamente a representação (1.35), encontramos que∫ LE ainda, analogamente ao que foi feito acima,∫ L000u ∗ nu ∗ n ′dx = LD∗ nD ∗ n ′ei(wn+w n ′ )t δ n,−n ′. (1.51)∫ Lu n u ∗ n ′dx = D n Dn ∗ ′e−i(wn−w n ′)t+i(kn−k n ′)x dx,0∫ L0u n u ∗ n ′dx = LD nDn ∗ ′δ n,n ′. (1.52)Retomando o nosso atual propósito, o de encontrarmos o valor da constante de normalizaçãoD n , podemos reescrever a equação (1.39) agora em termos das funções u n (x, t), ou seja∞∑ϕ(x, t) = [a n u n (x, t) + a ∗ nu ∗ n(x, t)]. (1.53)n=−∞A constante D n terá sua forma final definida por critérios físicos, mediante a Hamiltonianado oscilador. Para isso faremos uso das energias cinética e potencial já definidas para oformalismo em que estamos trabalhando. Temos então da equação (1.21) queT = 1 ∫ L( ) ( )∂ϕ ∂ϕ′dx,2v 2 ∂t ∂t013

e nesta, de acordo com a relação (1.48), que nos fornece as derivadas temporais da função u n ,temos queT = 12v 2 ∫ L0[ ∞∑n=−∞(−iw n a n u n + iw n a ∗ nu ∗ n)∞∑n ′ =−∞(−iw n ′a n ′ + iw n ′a ∗ n ′u∗ n ′) ]dxna qual, organizando os termos, temosT = 1 ∫ L ∞∑ ∞∑(−w2v 2 n w n ′a n a n ′u n u n ′ + w n w n ′a n a ∗ n ′u nu ∗ n ′+0n=−∞ n ′ =−∞+w n w n ′a ∗ na n ′u ∗ nu n ′ − w n w n ′a ∗ na ∗ n ′u∗ nu ∗ n ′)dx,que coerentemente com as relações (1.50), (1.51) e (1.52), toma a formaT = 12v 2∞∑∞∑n=−∞ n ′ =−∞[−w n w n ′a n a n ′D n D n ′Lδ n,−n ′e −i(wn+w n ′ ) + w n w n ′a n a ∗ n ′D nD ∗ n ′Lδ n,n ′++w n w n ′a ∗ na n ′D ∗ n ′D nLδ n,n ′ − w n w n ′a ∗ na ∗ n ′Lδ n,−n ′D∗ nD ∗ n ′ei(wn+w n ′) ]dx,e usando nesta a propriedade de filtragem da Delta, ou sejaa penúltima relação ficaT = 12v 2∞∑n=−∞∑ ∑f n,n ′δ n,n ′ = ∑ nnn ′f n (1.54)(−w 2 na n a −n D n D −n Le −2iwn + w 2 na n a ∗ nLD n D ∗ nl++w 2 na ∗ na n LD ∗ nD n − w 2 na ∗ na ∗ −nLD ∗ nD ∗ −ne 2iwn )dx,e, por fim, arrumando os termos, podemos escrever que a energia cinética é dada porT = L2v 2∞∑n=−∞(−w 2 na n a −n D n D −n e −2iwn + 2w 2 na ∗ na n |D n | 2 − w 2 na ∗ na ∗ −nD ∗ nD ∗ −ne 2iwn )dx. (1.55)Pela da equação (1.22), podemos escrever a energia potencial, cuja forma inicial seráV = 1 ∫ L( ) ( )∂ϕ ∂ϕ′dx,2 ∂x ∂x0que de acordo com a equação (1.49), que por sua vez nos fornece as derivadas espaciais dafunção u n , temosV = 1 2∫ L0∞∑∞∑n=−∞ n ′ =−∞(ik n a n u n − ik n a ∗ nu ∗ n)(ik n ′a n ′u n ′ − ik n ′a ∗ n ′u∗ n ′).14

Analogamente ao caso anterior, chegaremos na energia potencial dada porV = L 2∞∑n=−∞(k 2 na n a −n D n D −n e −2iwnt + 2k 2 na ∗ na n |D n | 2 + k 2 na ∗ na ∗ −nD ∗ nD ∗ −ne 2iwnt ). (1.56)Somando as energias cinéticas e potênciais do problema em quastão, obtemos a Hamiltonianado sistema, ou sejaH = T + V,de maneira que, de acordo com os resultados em (1.55) e (1.56), a Hamiltoniana ficaH = L 2∞∑n=−∞{( )( ) }kn 2 − w2 n(av 2 n a −n D n D −n e −2iwnt + a ∗ na ∗ −nDnD ∗ −ne ∗ 2iwnt ) + a ∗ na n kn 2 + w2 n|Dv 2 n | 2 ,na qual, finalmente, segundo a relação de dispersão, dada por (1.32), temos que a energia totaldo sistema, se reduzirá aH =∞∑n=−∞2w 2 nLv 2 |D n | 2 a ∗ na n . (1.57)Note que a constante D n deve se ajustar de tal maneira que garanta que o lado direito daúltima igualdade tenha dimensão de energia, então, para isso conclui-se que√vD n =2[γ], (1.58)2w n Lna qual γ é uma constante com dimensão de momento angular, assencial para que a igualdadeseja dimensionalmente consistente. LogoH =∞∑n=−∞[γ]w n a ∗ na n . (1.59)Então, a equação (1.46), já com o valor acima obtido para D n , toma a forma finalϕ(x, t) =∞∑n=−∞v[γ]√ 2wm L (a ne iknx−iwnt + a ∗ ne −iknx+iwnt ), (1.60)que é a solução geral para ondas que se propagam por uma corda sujeita às condições decontorno periódicas especificadas no início deste capítulo.15

1.2.2 Aspectos Gerais para a Quantização de Campos e a Quantizaçãoda CordaPara a quantização de campos, ou processo de segunda quantização, faremos uso do chamadoProcesso de Quantização Canônica, que consiste, basicamente, na substituição de variáveisclássicas dinâmicas por operadores lineares no espaço de Hilbert.Em sua forma clássica, as variáveis dinâmicas ϕ(x, t) e π(x, t), em termos do formalismoHamiltoniano, são escritas como[15]e˙ϕ(x, t) = δHδπ(1.61)˙π(x, t) = − δHδϕ , (1.62)sendo π, como já foi mensionado, é o momento canonicamente conjugado ao campo dado por(1.29).Essas grandezas no processo de quantização serão consideradas como operadores lineares,logo, para desde já designar isso, nos é conveniente denotá-las comoϕ(x, t) −→ ˆϕ(x, t)π(x, t) −→ ˆπ(x, t).(1.63)Uma outra importante questão para o processo de quantização é verificar se as grandezasenvolvidas são complementares ou não, ou seja, devemos verificar se as mesmas podem ou nãoserem medidas simultaneamente, para isso é importante verificar quais as relações de comutaçãoque as mesmas satisfazem. Essas relações de comutação quântica têm seus análogos clássicosnos Parêntese de Poisson[20].Do processo de primeira quantização[19], temos que[ˆp n , ˆx n ′] = −iδ n,n ′,[ˆp n , ˆp n ′] = 0, (1.64)[ˆx n , ˆx n ′] = 0,das quais podemos generalizar para campos e escrever, em tempos iguais, as relações de comutação[ˆπ(x, t), ˆϕ(y, t)] = −iδ(x − y)16

[ˆπ(x, t), ˆπ(y, t)] = 0 (1.65)[ ˆϕ(x, t), ˆϕ(y, t)] = 0,Note ainda que a Delta de Kronecker δ n,n ′ foi substituída pela Delta de Dirac δ(x − y), já quedeixamos sistemas discretos de distribuição e passamos para sistemas contínuos, o que se deveesperar de uma distribuição de campo.Coerente com o que foi feito até então, devemos também trocar as constantes a n e a ∗ n poroperadores, ou seja, implementar a mudançaa n −→ â na ∗ n −→ â † n.(1.66)comoEntão, diante de tais mudanças, a equação (1.60), já em sua forma de operador, fica escritaˆϕ(x, t) =∞∑n=−∞v[γ]√ 2wm L (â ne iknx−iwnt + â † ne −iknx+iwnt ), (1.67)e a Hamiltoniana, agora denominada como operador Hamiltoniano cujo autovalor é a energiatotal do sistema, ficaĤ =∞∑n=−∞w n [γ]↠nâ n . (1.68)Lembremos agora que no formalismo quântico a grandeza com dimensão de momento angularexplicita no operador Hamiltoniano é o próprio , o qual faremos igual à unidade assimcomo a velocidade da luz, segundo o chamado Sistema de Unidades Naturais, ou seja,Uma vez feito isso, teremos finalmente queˆϕ(x, t) =∞∑n=−∞ = c = 1. (1.69)v√ 2wm L (â ne iknx−iwnt + ↠ne −iknx+iwnt ) (1.70)e ainda∞∑Ĥ = w n â † nâ n . (1.71)n=−∞Perceba que a idéia de quantização canônica perpassa por um método, por um conjunto deprocedimentos específicos e necessários, e que a idéia de campo nada mais é do que uma funçãoque descreve o comportamento de uma oscilação em cada ponto do espaço.17

Capítulo 2A Quantização de Campos EscalaresNosso intuito neste capítulo é quantizar o campo escalar real e massivo, campo este regidopela chamada Equação de Klein-Gordon que, por sua vez, surgiu como uma tentativa de extensãoda Equação de Schödinger para sistemas que levassem em conta não somente a naturezaquântica, mas também a natureza relativística de um sistema qualquer.Neste capítulo também já usaremos os recursos técnicos/conceituais do Formalismo Lagrangeanopara campos, introduzido por nós, em parte, no capítulo anterior.2.1 A Equação de Klein-GordonA densidade de Lagrangeana que descreve a dinâmica de campos escalares, reais com massam, é dada por[8]L = 1 2 ∂µ ϕ∂ µ ϕ − 1 2 m2 ϕ 2 . (2.1)Tendo em mente a Equação de Euler-Lagrange para campos campos clássicos, dada pelarelação (1.23), e calculando cada termo desta, segundo a Lagrangeana dada acima, teremospara o primeiro termoe ainda,∂L∂ϕ = −m2 ϕ, (2.2)∂L∂∂ µ ϕ = 1 ∂2 ∂∂ µ ϕ (∂ν ϕ∂ ν ϕ) − 1 ∂2 ∂∂ µ ϕ m2 ϕ 2 ,note que o segundo termo da equação acima será nulo, uma vez que seu derivando não dependeexplicitamente das derivadas parciais do campo em questão. Assim sendo, calcularemos somente19

a derivada explicitada no primeiro termo da última equação, para isso introduziremos o tensormétrico dado porque abaixa e levanta índices, logog µν = g µν = diag(1, −1, −1, −1), (2.3)∂L∂∂ µ ϕ = 1 ∂2 gαν∂∂ µ ϕ (∂ αϕ∂ ν ϕ),e aplicando a regra da cadeia para as derivadas∂L∂∂ µ ϕ = 1 ( ∂∂α ϕ2 gαν ∂∂ µ ϕ ∂ νϕ + ∂ α ϕ ∂∂ )νϕ,∂∂ µ ϕe comotemos ainda∂∂ α ϕ∂∂ µ ϕ = δ αν,∂L∂∂ µ ϕ = 1 2 gαν (∂ ν ϕδ αµ + ∂ α ϕδ νµ ),que, usando a propriedade de filtragem das delta, ficaOrganizando os termos temos∂L∂∂ µ ϕ = 1 2 (gµν ∂ ν ϕ + g αµ ∂ α ϕ).∂L∂∂ µ ϕ = ∂µ ϕ,e, finalmente, aplicando as derivadas ∂ µ nesta última igualdade, obtemos∂ µ∂L∂∂ µ ϕ = ∂ µ∂ µ ϕ. (2.4)Reunindo os resulados (2.2) e (2.4) podemos escrever a equação de movimento para o campoescalar massivo dada porconhecida como a Equação de Klein-Gordon, onde(∂ 2 + m 2 )ϕ(x, t) = 0, (2.5)□ = ∂ µ ∂ µ = ∂ 2 , (2.6)20

que é o próprio operador D’Lambertiano definido agora segundo a notação relativística.Entendendo a última equação como sendo uma equação de onda, podemos inferir para estauma solução do tipo onda plana dada porϕ(x, t) =∞∑n=−∞c n e i(knx−wnt) . (2.7)Iremos impor condições de contorno para o campo em questão semelhantemente ao foi feitopara o caso da corda. Porém, para este caso, consideraremos o campo contido num certo volumeL 3 , sendo nulo o valor do campo na superfície deste cubo.Por mais que agora estejamosinteressados no caso tridimensional, proseguiremos com os cálculos numa única direção, demaneira que, após isto, possamos fazer a generalização para o caso de três dimensões espaciaissem maiores complicações.Substituindo a solução proposta em (2.7) na equação de Klein-Gordon, temos( )∂2∂t − ∂22 ∂x + 2 m2∞∑n=−∞c n e i(knx−wnt) = 0ou ainda, já tendo efetuado as derivadas indicadas nesta última equaçãoDe onde concluimos que∞∑n=−∞c n e i(knx−wnt) (−w 2 n + k 2 n + m 2 ) = 0.w 2 n = k 2 n + m 2 , (2.8)relação esta de extrema importância, essencial para que a solução (2.7) seja de fato solução daequação de Klein-Gordon.2.2 A Quantização do Campo Escalar sujeito à Condiçõesde Contorno PeriódicasDe maneira similar ao método seguido no capítulo anterior para a quantização da corda,cujo campo é dado pela equação (1.60), pode-se mostrar que a equação que rege o campo emquestão é dado porˆϕ(⃗x, t) =∞∑n=−∞1√ 2wm L 3 (â ne i⃗ k n·⃗x−iw nt + â † ne −i⃗ k n·⃗x+iw nt ), (2.9)21

ou ainda, em termos da equação (1.47), por∞∑ˆϕ(⃗x, t) = [â n u n (⃗x, t) + â † nu ∗ n(⃗x, t)], (2.10)n=−∞sendo que as relações de comutação que esta solução, já generalizada para três dimensõesespaciais, deve satisfazer, assim como seu momento canonicamente cojugado, são dadas tambémpor (1.65).Comparando (2.10) com a equação (1.60), percebemos que a velocidade envolvida é a própriavelocidade da luz, usada aqui no sistema de unidades naturais. Sendo ainda que⃗ kn = (k 1 , k 2 , k 3 ),⃗x = (x 1 , x 2 , x 3 ),(2.11)uma vez que estamos considerando o espaço tridimensional.2.2.1 O Operador HamiltonianoMesmo de posse da técnica já desenvolvida no capítulo anterior, aqui encontraremos a formaexplícita do Hamiltoniano em questão desenvolvendo uma outra técnica e explicitando sutilezasde cálculo ainda não mostradas.Comecemos pelo chamado Produto Escalar de Klein-Gordon[5], definido 1 para doisescalares ϕ 1 e ϕ 2 , comosendo∫ L 3↔(ϕ 1 , ϕ 2 ) = −i ϕ 1 ∂ 0 ϕ ∗ 2dx 3 , (2.12)0A ↔ ∂ 0 B = A ∂B∂t − ∂A∂t B.Com a definição acima, calcularemos algumas importantes relações para as funções u n , jágeneralizada para o caso tridimensional, no qual L → L 3 e dx → dx 3 . Começando por (u n , u ∗ n ′),temosque, conforme (1.48), fica∫ L 3(u n , u ∗ n ′) = −i (u n ∂ 0 u n ′ − ∂ 0 u n u n ′)dx 3 ,0∫ L 3(u n , u ∗ n ′) = −i (−iw n ′u n u n ′ + iw n u n u n ′)dx 3 ,01 Esta definição decorre naturalmente da condição de normalização imposta sobre os campos, para o caso emque existe um fluxo de corrente de probabilidade através da superfície que define um volume L 3 qualquer.22

ou aindaque, usando a equação (1.50), ficaque segundo (1.44) fica∫ L 3(u n , u ∗ n ′) = (w n u n u n ′ − w n ′u n u n ′)dx 3 ,0= (w n − w n ′)∫ L 30u n u n ′dx 3 ,(u n , u ∗ n ′) = (w n − w n ′)D n D n ′e −i(wn+w n ′ )t L 3 δ n,−n ′,(u n , u ∗ n ′) = 0. (2.13)Calculando ainda (u n , u n ′), analogamente ao caso anterior, temos(u n , u n ′) = −i= −i∫ L 30∫ L 30= (w n + w n ′)(u n ∂ 0 u ∗ n ′ − ∂ 0u n u ∗ n ′)dx3 ,(iw n ′u n u ∗ n ′ + iw nu n u ∗ n ′)dx3 ,∫ L 3que de acordo com a equação (1.52), fica na formaque devido a (1.54), fica0u n u ∗ n ′dx3 ,(u n , u n ′) = (w n + w n ′)D n D ∗ n ′L3 δ n,n ′,(u n , u n ′) = 2w n L 3 |D n | 2 ,como as funções u n são ortonormais entre si, temos para isto queD n =1√ 2wn L 3 , (2.14)que é justamente a constante de normalização, encontada de maneira imediata partindo dadefinição do produto escalar de Klein-Gordon. Logo(u n , u n ′) = δ n,n ′. (2.15)Para explicitar a forma dos operadores â n e â † n, em termos do campo ϕ(⃗x, t), vamos aplicarna equação (2.10), pela esquerda, por∫ L 3−i u n ′0↔∂ 0 dx 3 ,23

assim fazendo temos∫ L 3−i u n ′0↔∂ 0 ˆϕdx 3 =∞∑n=−∞(−iâ n∫ L 30u n ′∫↔L 3∂ 0 u n dx 3 − iâ † n u n ′0)↔∂ 0 u ∗ ndx 3 .Note nesta última, que podemos identificar o produto de Klein-Gordon, dado por (2.12),definido agora para as funções u n e u ∗ n, assim∫ L 3−i u n ′0↔∂ 0 ˆϕdx 3 =∞∑n=−∞Então, segundo as relações (2.13) e (2.15), temosou ainda∫ L 3−i u n ′0↔∂ 0 ˆϕdx 3 = −Efetuando agora a multiplicação do operador[â n (u n ′, u n ) − â † n(u n ′, u ∗ n)].∞∑n=−∞â † nδ n,n ′,∫ L 3â † ↔n = −i u n ∂0 ˆϕdx 3 . (2.16)0pela direita de (2.10), temos∫ L 3−i0ˆϕ ↔ ∂ 0 u ∗ n ′dx3 ==∞∑n=−∞∞∑n=−∞∫ L 3−i0(−iâ n∫ L 30↔∂ 0 u ∗ n ′u n ′[â n (u n ′, u n ) − â † n(u n ′, u ∗ n)],∫ )↔L 3∂ 0 u ∗ ndx 3 − iâ † n u ∗ ↔n ′ ∂0 u ∗ ndx 3 ,0que, analogamente ao caso anterior, se escreverá na forma∫ L 3â n = −i0ˆϕ ↔ ∂ 0 u ∗ ndx 3 . (2.17)Com isso, podemos encontrar algumas relações de comutação importantes que â nobedecem. Vamos começar introduzindo as seguintes notações:{ ˆϕ(⃗y, t) = ˆϕ′e â † nˆπ(⃗y, t) = ˆπ ′ ,Então, para a relação [â n , â n ′], temos[â n , â n ′] = â n â n ′ − â n ′â n ,24

que segundo (2.16) e (2.17), fica∫ L 3[â n , â n ′] = −=0∫ L 3 ∫ L 300ˆϕ ↔ ∂ 0 u ∗ ndx 3 ∫ L 30ˆϕ ′ ↔∂0 u ∗ n ′dy3 −Usando o produto escalar de Klein-Gordon, temos[â n , â n ′] =∫ L 3 ∫ L 300∫ L 30ˆϕ ′ ↔∂0 u ∗ n ′dy3 ∫ L 3[( ˆϕ ′ ↔∂0 u ∗ n ′)( ˆϕ ↔ ∂ 0 u ∗ n) − ( ˆϕ ↔ ∂ 0 u ∗ n)( ˆϕ ′ ↔∂0 u ∗ n ′)]dx3 dy 3 .0ˆϕ ↔ ∂ 0 u ∗ ndx 3[( ˆϕ ′ ∂ 0 u ∗ n ′ − ∂ 0 ˆϕ ′ u ∗ n ′)( ˆϕ∂ 0u ∗ n − ∂ 0 ˆϕu ∗ n) − ( ˆϕ∂ 0 u ∗ n − ∂ 0 ˆϕu ∗ n)( ˆϕ ′ ∂ 0 u ∗ n ′ − ∂ 0 ˆϕ ′ u ∗ n ′)]dx3 dy 3 ,que segundo as derivadas temporais das funções u n , dada por (1.48), fica[â n , â n ′] =∫ L 3 ∫ L 300[(iw n ′ ˆϕ ′ u ∗ n ′ − ˆπ′ u ∗ n ′)(iw n ˆϕu ∗ n − ˆπu ∗ n) − (iw n ˆϕu ∗ n − ˆπu ∗ n)(iw n ′ ˆϕ ′ u ∗ n ′ − ˆπ′ u ∗ n ′)]dx3 dy 3 .Multiplicando os fatores da equação acima e, após isso, identificando nesta as relações decomutação, temos[â n , â n ′] =∫ L 3 ∫ L 300(w n w n ′[ ˆϕ, ˆϕ ′ ]u ∗ n ′u∗ n + iw n ′[ˆπ, ˆϕ ′ ]u ∗ nu ∗ n ′ + [ ˆϕ′ , ˆϕ]u ∗ n ′u∗ n + iw n [ ˆϕ, ˆπ ′ ]u ∗ nu ∗ n ′)dx3 dy 3 ,na qual, considerando as relações dadas por (1.59), resulte∫ L 3[â n , â n ′] = i0∫ L 30= (w n ′ − w n )[−iw n ′δ(⃗x − ⃗y) + iw n δ(⃗x − ⃗y)]u ∗ nu ∗ n ′dx3 dy 3∫ L 3 ∫ L 300δ(⃗x − ⃗y)u ∗ n(⃗x, t)u ∗ n ′(⃗x′ , t)dx 3 dy 3 .Usando a propriedade de filtragem da Delta de Dirac[3][4], dada portemos quef(a) =∫ xx 0f(x)δ(x − a)dx, (2.18)∫ L 3[â n , â n ′] = (w n ′ − w n ) u ∗ nu ∗ n ′dx3 ,0teremos portanto, de acordo com a relação (1.44), que[â n , â n ′] = (w n ′ − w n )L 3 D n D n ′e −i(wn+w n ′ )t δ n,−n ′,levando novamente em conta (2.18), temos que[â n , â n ′] = 0. (2.19)25

Para a relação [â † n, â † n ′ ], vem que[â † n, â † n ′ ] = â † nâ † n ′ − â † n ′ â † n.Sabendo que[19]: ( ˆB) † = ˆB †  † e ( + ˆB) † = † + ˆB † , podemos escrever[â † n, â † n ′ ] = (â n ′â n ) † − (â n â n ′) †= (â n ′â n − â n â n ′) †= ([â n ′, â n ]) † .Logo, de acordo com a última relação de comutação (2.19) obtemos[â † n, â † n ′ ] = 0. (2.20)Nos falta ainda obter a regra de comutação para [â n , â † n ′ ], para isso façamosque, de acordo com (2.16) e (2.17), ficae ainda∫ L 3[â n , â † n] = −′ 0[â n , â † n ′ ] =∫ L 3 ∫ L 300ˆϕ ↔ ∂ 0 u ∗ ndx 3 ∫ L 3[â n , â † n ′ ] = â n â † n ′ − â † n ′ â n ,0u n ′∫↔L 3∂ 0 ˆϕ ′ dy 3 + u n ′0∫↔L 3∂ 0 ˆϕ ′ dy 30ˆϕ ↔ ∂ 0 u ∗ ndx 3 ,[(u n ′∂ 0 ˆϕ ′ − ∂ 0 u n ′ ˆϕ ′ )( ˆϕ∂ 0 u ∗ n − ∂ 0 ˆϕu ∗ n) − ( ˆϕ∂ 0 u ∗ n − ∂ 0 ˆϕu ∗ n)(u n ′∂ 0 ˆϕ ′ − ∂ 0 u n ′ ˆϕ ′ )]dx 3 dy 3 ,na qual, calculando os produtos da relação acima, identificamos algumas relações de comutaçãoimportantes entre os operadores de campo e os momentos cononicamente conjugados à eles, demodo que podemos escrever esta como[â n , â † n ′ ] =∫ L 3 ∫ L 300(iw n [ˆπ ′ , ˆϕ]u n ′u ∗ n + [ˆπ, ˆπ ′ ]u n ′u ∗ n + w n ′w n [ ˆϕ, ˆϕ ′ ]u n ′u ∗ n + iw n ′[ˆπ, ˆϕ ′ ]u n ′u ∗ n)dx 3 dy 3 ,que, segundo as relações de comutação dadas por (1.65), ficae que de acordo com (2.18), temos∫ L 3 ∫ L 3[â n , â † n] = (w ′ n + w n ′) δ(⃗x − ⃗y)u n ′u ∗ ndx 3 dy 3 ,0 0∫ L 3[â n , â † n] = (w ′ n ′ + w n ) u ∗ nu n ′dx 3 ,026

e com a relação (1.45), já substituindo o valor da constante de normalização D n , chegaremosem[â n , â † n ′ ] = (w n ′ + w n)2w n L 3 L 3 δ n,n ′,da qual, analisando seus valores para n = n ′ e n ≠ n ′ , podemos escrever[â n , â † n ′ ] = δ n,n ′. (2.21)Então, as relações de comutação obedecidas por â n e â † n podem ser reunidas em um conjunto,segundo cada par de operadores, dadas por[â n , â n ′] = 0,[â † n, â † n ′ ] = 0, (2.22)[â n , â † n ′ ] = δ n,n ′,que, por sua vez, dá suporte para a relação dada em (1.65) entre os observáveis ˆϕ e ˆπ, que sãoas quantidades físicamente relevantes para o nosso problema.Vamos agora analisar o chamado Tensor Energia-Momento θ µν [18], que para o campoem questão é dado porθ µν =∂L∂∂ µ ϕ ∂ν ϕ − g µν Lque de acordo com a igualdade(2.4), fica∂L∂∂ µϕ= ∂µ ϕ, já encontrada anteriormente segundo a relaçãoθ µν = ∂ µ ϕ∂ ν ϕ − g µν L, (2.23)e uma vez que, agora, a densidade de Lagrangeana é dada por (2.1), temosθ µν = ∂ µ ϕ∂ ν ϕ − g µν ( 12 ∂λ ϕ∂ λ ϕ − 1 2 m2 ϕ 2 ), (2.24)que é uma forma mais explicita do tensor energia-momento para o campo aqui considerado.Este tensor é um elemento fundamental para a relatividade e, portanto, para a teoria decampos. Trata-se de uma grandeza que é conservada, obtida e definida através do Teoremade Noether[8], que relaciona simetrias do espaço-tempo com leis de conservação de grandezasfísicas, de maneira que para cada simetria do espaço-tempo há uma grandeza física conservada.27

+(m 2 + w n w n ′ + k n k n ′)â n â † n ′ u n u ∗ n ′ + (m2 + w n w n ′ + k n k n ′)â † nâ n ′u ∗ nu n ′].Substituindo este último resultado na equação (2.25), teremos, basicamente, que calcular integraisdas funções u n e seus complexos conjugados u ∗ n. Daí, levando em conta os resultadosobtidos em (1.50), (1.51) e (1.52), obtemosĤ =∞∑n=−∞[(m 2 − w 2 n − k 2 n)â † nâ † −nD ∗ nD ∗ −ne 2iwnt L (2.29)+(m 2 −w 2 n−k 2 n)â n â −n D n D −n e −2iwnt L+(m 2 +w 2 n+k 2 n)â † nâ n |D n | 2 L+(m 2 +w 2 n+k 2 n)â n â † n |D n | 2 L].Então, de acordo com a relação (2.8) e a constante de normalização dada por (2.14), obtemosĤ =∞∑n=−∞que, como [â n , â † n] = 1 ⇒ â n â † n = 1 + â † nâ n , ficaĤ =∞∑n=−∞que representa a energia total de infinitos osciladores harmônicos.Aplicando o operador Hamiltoniano no estado |n〉, temos12 (↠nâ n + â n â † n)w n , (2.30)(w n â † nâ n + 1 ). (2.31)2Ĥ |n〉 = E |n〉 (2.32)na qual o autovalor da energia, segundo resultados já conhecidos de acordo com a físicaquântica[7], é dado porE =∞∑n=−∞(w n n + 1 ), (2.33)2e segundo atribuições de um novo operador, cujo autovalor é o número de quanta presente emseu autoestado, definiremos este como Operador Numeral, que é escrito comoˆN = â † nâ n , (2.34)de forma queˆN |n〉 = n |n〉 . (2.35)Antes de proseguirmos com nossa análise a respeito do operador Hamiltoniano, nos é convenienteentendermos um pouco mais acerca dos operadores â n e â † n, tais como suas relações de29

comutação com o operador numeral, e o resultado obtido na aplicação deles, separadamente,no estado |n〉. Neste sentido, vamos obter[ ˆN, â] = [â † â, â]= â † ââ − ââ † â= (â † â − ââ † )â= [â † , â]â= −â,(2.36)e ainda[ ˆN, â † ] = [â † â, â † ]= â † ââ † − â † â † â= â † (ââ † − â † â)= â † [â, â † ]= â † .(2.37)Fazendo a aplicação de (2.36) sobre |n〉, segue que[ ˆN, â] |n〉 = −â |n〉( ˆNâ − â ˆN) |n〉 = −â |n〉ˆNâ |n〉 − ân |n〉 = −â |n〉ˆNâ |n〉 = (n − 1)â |n〉 ,(2.38)de maneira que podemos entender que â atua em |n〉 de forma a retirar deste um quanta deenergia, e por esse motivo, é chamado de Operador Aniquilação.Chamando |m〉 = â |n〉, podemos reescrever (2.38) comoˆN |m〉 = (n − 1) |m〉 , (2.39)e considerando que a relação (2.39) seja uma equação de autovalor, o estado |m〉 será dado por|m〉 = C |n − 1〉 , (2.40)sendo C um número qualquer a ser definido e introduzido aqui de tal maneira que garantaa generalização do resultado obtido até então. Efetuando o produto escalar entre a equação(2.40) e sua correspondente dual, temos que〈n| â † â |n〉 = 〈n − 1| C ∗ C |n − 1〉 ,e notando nesta última expressão que â † â é a definição do operador numeral, que por sua vezatuará diretamente sobre o estado |n〉 de acordo com (2.35), assim sendo podemos encontrarqueC = √ n. (2.41)30

Então, podemos escreverâ |n〉 = √ n |n − 1〉 , (2.42)que de maneira análoga ao que fizemos para encontrar a relação (2.42), comecemos por fazer[ ˆN, â † ] |n〉 = [â † , â † ] |n〉( ˆNâ † − â † ˆN) |n〉 = â † |n〉ˆNâ † |n〉 = (n + 1)â † |n〉 ,(2.43)e podemos entender que â † atua em |n〉 de forma a fornecer um quanta de energia ao osciladorharmônico, e é denominado, por esse motivo, de Operador Criação.Prosseguindo, ainda analogamente ao caso anterior, encontraremos agora o valor de umaconstante C ′ utilizando o mesmo argumento feito para a obtenção de C. Assim fazendo obtemosde onde segue queC ′ = √ n + 1, (2.44)â † |n〉 = √ n + 1 |n + 1〉 . (2.45)Com isso podemos obter qualquer estado |n〉 fazendo sucessivas aplicações do operador â †no estado |0〉, ou seja, de forma geral temos|n〉 = (↠) n√n!|0〉 , (2.46)sendo |0〉 o estado do vácuo que representa um estado com o menor conteúdo possível, seja deenergia, seja de partículas. Essas operações são definidas apenas para n ≥ 0, com a seguinteressalvaâ |0〉 = 0, (2.47)pois assim, garantimos que o produto escalar entre os autoestados aqui considerados sejampositivos definidos e a não possibilidade de destruição de partículas onde elas, a princípio, nãoexistem.Medindo o autovalor de energia do vácuo, temos queĤ |0〉 = E 0 |0〉 , (2.48)sendo E 0 o autovalor de energia desse estado, que de acordo com a relação (2.33), será dadaporE 0 =∞∑n=∞3112 w n (2.49)

Nesta última equação vemos que o vácuo apresenta, em virtude da somatória sobre todosos modos normais, uma energia infinita.Para contornarmos isso, iremos propor, para estecaso, o denominado Ordenamento Normal que, basicamente, remove termos divergentes quesurgem eventualmente quando se tem produtos entre operadores calculados num mesmo pontodo espaço. O ordenamento normal se justifica uma vez que, experimentalmente, o que se medesão diferenças de energia, não a energia absoluta do sistema. Desta maneira torna-se necessárioescolher um estado diante do qual todas as diferenças de energia são computadas, um estado dereferência, que denominamos de vácuo. O ordenamento normal estipula, basicamente, a ordemcom que os operadores devem ser aplicados de forma que não resultem em divengências.Para melhor entendermos tal ordenamento, reescreveremos a solução (2.10), já encontradaanteriormente, comoˆϕ(⃗x, t) = ˆϕ (+) + ˆϕ (−) , (2.50)na qual ˆϕ (+) está associado com a parte de criação de partículas e ˆϕ (−) com a parte deaniquilação. O ordenamento normal entre dois operadores ˆϕ(⃗x, t) e ˆψ(⃗y, t), sendo este escritode maneira semelhante a relação (2.50), é definido como [9]: ˆϕ(⃗x, t) ˆψ(⃗y, t) := ˆϕ (+) ˆψ(+) + ˆϕ (+) ˆψ(−) + ˆψ (+) ˆϕ (−) + ˆϕ (−) ˆψ(−) , (2.51)de maneira que não apresente a dificuldade mensionada ao tomarmos o limite de ⃗x tendendopara ⃗y. De forma mais prática, essa operação consiste em reescrevermos os operadores de talforma que as partes de aniquilação venham após as partes de criação. Logo, aplicando esteordenamento na equação (2.31), teremos quede onde vem que: Ĥ := ∞∑n=−∞Ĥ =12 : (↠nâ n + â n â † n) : w n ,∞∑n=−∞w n â † nâ n , (2.52)nos fornecendo o operador hamiltoniano conforme o ordenamento normal.Como o que realmente nos importa é a variação da energia e não seu valor absoluto, buscaremosno vácuo uma boa referência para trabalharmos. Aplicando a equação (2.52) no estadode vácuo, teremosĤ |0〉 =∞∑n=−∞w n â † nâ n |0〉 ,32

e daí tiramos queE 0 = 0,o que é um bom ponto de referência para trabalharmos com a energia, uma vez que o valorabsoluto que encontraremos para esta será sua própria variação se considerarmos o vácuo comotal ponto de referência.2.3 A Quantização do Campo Escalar LivreProseguiremos agora com a quantização do campo escalar livre, o qual, diferentemente doque foi feito até então, não está sujeito à condições de contorno. O campo em questão tambémé regido pela equação de Klein-Gordon, para este proporemos a seginte solução[9]∫ˆϕ(⃗x, t) = dk 3 N k e i⃗ k·⃗xâk (t), (2.53)sendo N k uma constante de normalização a ser determinada. Esta solução segue a mesmaestrutura daquela proposta em (1.33) e na qual se distingue pela soma contínua sobre todos osmomentos ⃗ k.Substituindo a equação (2.53) na equação de Klein-Gordon (2.5), teremos( ) ∂2∫∂t − 2 ∇2 + m 2 dk 3 N k e i⃗ k·⃗xâk (t) = 0,aplicando as devidas derivadas espaciais e temporais no integrando da solução, virá que∫∫∫dk 3 N k e i⃗ k·⃗x¨âk (t) + ⃗ k 2 dk 3 N k e i⃗ k·⃗xâk (t) + m 2 dk 3 N k e i⃗ k·⃗xâk (t) = 0,e arrumando os termos, temos que∫dk 3 N k e i⃗ k·⃗x [¨â k (t) + ( ⃗ k 2 + m 2 )â k (t)] = 0.Sendo que, desta última equação, tiramos que¨â k (t) + ( ⃗ k 2 + m 2 )â k (t) = 0, (2.54)e aindawk 2 = ⃗ k 2 + m 2 , (2.55)onde surge uma relação entre a massa do campo e a energia relativística.33

A solução da equação diferencial (2.54) poderá ser escrita comoâ k (t) = â (1)k e−iw kt + â (2)k eiw kt , (2.56)e, analogamente ao que foi feito anteriormente, de acordo com a condição para termos umasolução física, chegamos à conclusão queâ (2)k= [â (1)k ]† . (2.57)Então a equação (2.53) fica na forma∫ˆϕ(⃗x, t) = dk 3 N k (â k e i⃗ k·⃗x−iw k t + â † k e−i⃗ k·⃗x+iw k t ), (2.58)e o momento canonicamente conjugado ao campo, conforme (1.30), será dado por∫ˆπ(⃗x, t) = i dk 3 N k w k (â † k e−i⃗ k·⃗x+iw k t + â k e i⃗ k·⃗x−iw k t ). (2.59)Como já nos referimos anteriormente, â † k e â k são os operadores de criação e aniquilaçãoque satisfazem as relações de comutação mostradas em (2.22). Os operadores ˆϕ(⃗x, t) e ˆπ(⃗x, t)satisfazem as relações de comutação que surgem de acordo com o princípio da correspondência(dadas para tempos iguais), relações estas essenciais para a determinação da constante N k .Façamos então, usando (2.58) e (2.59), o comutador∫∫[ˆπ(⃗x, t), ˆϕ(⃗y, t)] = i dk 3 N k w k (â † k e−i⃗ k·⃗x+iw k t + â k e i⃗ k·⃗x−iw k t )dk ′3 N k ′(â k ′e i⃗ k ′·⃗y−iw k ′ t + â † k ′ e −i⃗ k ′·⃗y+iw k ′ t )+∫−i∫dk ′3 N k ′(â k ′e i⃗ k ′·⃗y−iw ′t k+ â † ke −i⃗ k ′·⃗y+iw k ′ ′ t )dk 3 N k w k (â † k e−i⃗ k·⃗x+iw k t + â k e i⃗ k·⃗x−iw k t ).Após multiplicarmos os fatores da última equação e, identificando nesta alguns comutadores jáconhecidos, temos∫ ∫[ˆπ(⃗x, t), ˆϕ(⃗y, t)] = i dk 3 N k w k dk ′3 N k ′{[â † k , â k ′]e−i(⃗ k·⃗x−k ⃗′·⃗y)+i(w k −w k ′ )t ++[â † k , ↠k]e i(⃗ k·⃗x+ k ⃗′·⃗y)+i(w k +w k ′ ′ )t + [â k , â k ′]e i(⃗ k·⃗x+ k ⃗′·⃗y)−i(w k +w ′)t k+ [â † k, â ′ k ]e i(⃗ k·⃗x−k ⃗′·⃗y)−i(w k −w ′)t k},e finalmente, usando as relações (2.22), temos∫ ∫[ˆπ(⃗x, t), ˆϕ(⃗y, t)] = −i dk 3 N k w k dk ′3 N k[δ ′ 3 (k − k ′ )e −i(⃗ k·⃗x− ⃗ k ′·⃗y)+i(w k −w ′)t k++δ 3 (k − k ′ )e i(⃗ k·⃗x− ⃗ k ′·⃗y)−i(w k −w k ′ )t ],34

que, segundo (2.18), fica∫[ˆπ(⃗x, t), ˆϕ(⃗y, t)] = −idk 3 N k w k [e −i⃗ k·(⃗x−⃗x ′) + e i⃗ k·(⃗x−⃗y) ].Como uma das representações da Delta de Dirac é dada por[4]δ 3 (⃗x) = 1 ∫e i⃗k·⃗x dk 3 , (2.60)(2π) 3teremos que[ˆπ(⃗x, t), ˆϕ(⃗y, t)] = −iN 2 k w k 2(2π) 3 δ 3 (⃗x − ⃗x),e quando levamos em consideração a relação de comutação já exibida anteriormente em (1.65),conclui-se queN k =1√2wk (2π) 3 . (2.61)Então, o operador campo e seu momento canonicamente conjugado podem ser escritos como∫ˆϕ(⃗x, t) = dk 3 [â k u k (⃗x, t) + â † k u∗ k(⃗x, t)], (2.62)esendo∫ˆπ(⃗x, t) = idk 3 w k [â † k u∗ k(⃗x, t) − â k u k (⃗x, t)], (2.63)u k (⃗x, t) =ei⃗ k·⃗x−iw k t√2wk (2π) 3 . (2.64)Note nas expressões obtidas acima que ao submetermos um campo livre à condições decontorno, como foi feito anteriormente, estamos basicamente trocando[9][13]∫dk 3(2π) 3 2→∞∑n=−∞1L 3 . (2.65)Já para o operador Hamiltoniano, da mesma maneira que encontramos anteriormente, esteserá dado por∫Ĥ =θ 00 dx 3 , (2.66)ou ainda, substituindo nesta a componente θ 00 de (2.24), temosĤ = 1 ∫[(∂ 0 ˆϕ) 2 + (∂ j ˆϕ) 2 + m 2 ˆϕ 2 ]dx 3 , (2.67)235

logo, substituindo nesta última equação do campo dado por (2.62) e suas respectivas derivadastemporais e espaciais, dadas por (2.27) e (2.28), multiplicando os fatores desta e arrumandoseus termos, temosĤ = 1 ∫ ∫ ∫dx 3 dk ′3 dk 3 [(−w k ′w k − | k2⃗′ || ⃗ k| + m 2 )â † kâ † ′ k u∗ k ′u∗ k++(−w k ′w k − | ⃗ k ′ || ⃗ k| + m 2 )â k ′â k u k ′u k + (w k ′w k + | ⃗ k ′ || ⃗ k| + m 2 )â † k ′ â k u ∗ k ′u k++(w k ′w k + | ⃗ k ′ || ⃗ k| + m 2 )â k ′â † k u k ′u∗ k].Calculando agora as integrais em ⃗x presentes em cada termo da última relação começandopela integral da função u k , dada por (2.64) e de seu complexo conjugado u ∗ k ′. Assim, já organizandoalguns termos, temos∫dx 3 u ∗ k ′u k = 1(2π) 3 ∫que de acordo com (2.60), fica∫dx 3 1 1√ √ e i(w k ′ −wk)t e i⃗x·(⃗ k− ⃗ k ′) ,2wk ′ 2wkdx 3 u ∗ k ′u k = δ3 ( ⃗ k − ⃗ k ′ )√ 2wk√ 2wk ′e i(w k ′ −w k)t . (2.68)Calculando agora para u ∗ k e ′ u∗ k , temos∫∫dx 3 u ∗ k ′u∗ k = dx 3 1 1√ √ e i(w k ′ +wk)t e −i⃗x.(⃗ k+ ⃗ k ′) ,2wk ′ 2wkque analagamente ao caso anterior, fica∫dx 3 u ∗ k ′u∗ k = δ3 ( ⃗ k + ⃗ k ′ )√ 2wk√ 2wk ′e i(w k ′ +w k)t , (2.69)e ainda para u k e u k ′, de onde vem∫∫dx 3 u k ′u k =dx 3 1 1√ √ e −i(w′ k +wk)t e i⃗x.(⃗ k+ ⃗ k ′) ,2wk ′ 2wkque fica como∫dx 3 u k ′u k = δ3 ( ⃗ k + ⃗ k ′ )√ 2wk√ 2wk ′e −i(w k ′ +w k)t . (2.70)Com as relações (2.68), (2.69) e (2.70), podemos mostrar, concordando com (2.18), queĤ = 1 ∫ dk3[(−wk 2 + |2 2w ⃗ k| 2 + m 2 )â † −k↠k e2iw kt + (−wk 2 + | ⃗ k| 2 + m 2 )â −k â k e −2iwkt +k36

+(wk 2 + | ⃗ k| 2 + m 2 )â † kâk + (wk 2 + | ⃗ k| 2 + m 2 )â k â † k ],e finalmente, segundo a equação (2.55), teremosĤ = 1 ∫ dk32w2 2wk(â 2 † kâk + â k â † k), (2.71)kque após considerarmos para esta o produto ordenamento normal, a mesma fica∫Ĥ = dk 3 w k â † kâk, (2.72)que é o operador Hamiltoniano para o campo escalar livre, similar ao caso anterior, onde taloperador é dado por (2.52).37

Capítulo 3A Quantização do CampoEletromagnéticoApresentaremos agora a quantização do campo eletromagnético não massivo que, por suavez, tem um nível de complexidade um tanto maior do que já foi feito anteriormente parao caso do campo escalar. Para este caso será necessário impormos uma escolha de calibre.Tal procedimento ficará mais claro no decorrer deste trabalho, onde quantizaremos este campotanto via calibre do Coulomb quanto via calibre de Lorentz. Aqui também teremos a implicaçãofundamental da polarização, que é discutida pormenorizadamente no texto, além de termosdedicado um Apêndice para bem tratá-la matematicamente.3.1 O Campo de MaxwellÉ possível mostrar que o campo eletromagnético é descrito pela densidade de Lagrangeana[8][10]L = − 1 4 F µνF µν − j µ A µ , (3.1)na qual F µν é o chamado tensor de Maxwell, A µ o quadri-potencial e j µ a quadri-densidade decorrente .No vácuo, onde são nulas as distribuições de cargas e correntes, ou considerando ainda queo campo não interage com nenhuma fonte de carga, teremos simplesmenteL = − 1 4 F µνF µν . (3.2)Onde o tensor de Maxwell pode também ser dado por[10]F µν = ∂ µ A ν − ∂ ν A µ , (3.3)38

cujos elementos são componentes dos campos elétrico e do vetor indução magnética. Logo, adensidade de Lagrangeana, escrita em termos de (3.3), ficaL = − 1 4 (∂ µA ν − ∂ ν A µ )(∂ µ A ν − ∂ ν A µ ). (3.4)Substituindo a equação (3.4) na equação de Euler-Lagrange dada por (1.23), consideradaagora para o campo A µ , esta ficará∂L ∂L− ∂ β = 0. (3.5)∂A σ ∂∂ β A σCalculando termo a termo dessa expressão, teremos, para o primeiro termo, que∂L= − 1 ∂[(∂ µ A ν − ∂ ν A µ )(∂ µ A ν − ∂ ν A µ )],∂A σ 4 ∂A σnote nesta última equação, que a função que será derivada não depende explicitamente docampo A σ , mas sim das derivadas deste, entãoE ainda, para o segundo termo, temos∂L∂A σ= 0. (3.6)∂L= − 1 ∂[(∂ µ A ν − ∂ ν A µ )(∂ µ A ν − ∂ ν A µ )],∂∂ β A σ 4 ∂∂ β A σque, segundo o tensor métrico, pode ser escrito como∂L= − 1 ∂[(∂ µ A ν − ∂ ν A µ )(g µη g νγ ∂ η A γ − g νρ g µϑ ∂ ρ A ϑ )],∂∂ β A σ 4 ∂∂ β A σsendo o tensor métrico g µν , a métrica de Mikowski dada por (2.3).Utilizando-se da regra do produto para derivadas e atentando ainda quepodemos escrever queportanto, aplicando ainda a quadri-divergência ∂ β , temos∂ β∂∂ µ A ν∂∂ β A σ= δ µβ δ νσ , (3.7)∂L∂∂ β A σ= −F βσ , (3.8)∂L= −∂ β F βσ . (3.9)∂∂ β A σEntão, de acordo com os resultados (3.6) e (3.9), a equação de Euler-Legrange dada por(3.5), fica∂ µ F µν = 0, (3.10)39

que corresponde às leis de Gauss e Ampère, ou seja, corresponde, respectivamente, àeque, complementadas com as equações contidas em∇ · ⃗E = 0 (3.11)∇ × ⃗ B = ∂ ⃗ E∂t , (3.12)∂ [ σF µν] = 0, (3.13)que são, respectivamente, a Lei de Faraday e a Lei do monopólo magnetico, explicitamentedados por∇ × ⃗ E = − ∂ ⃗ B∂t(3.14)e∇ · ⃗B = 0, (3.15)constituem as chamadas equações de Maxwell no caso em que ρ e ⃗j são nulos[12].3.2 A Quantização do Campo Eletromagnético via Calibrede CoulombEm concordância com a equação (3.10), em termos de (3.3), esta pode ser escrita comoou ainda de acordo com (2.6) comoPara ν = i, na equação (3.16), temos que∂ µ (∂ µ A ν − ∂ ν A ν ) = 0,Impondo sobre esta última o calibre de Coulomb dado por□A ν − ∂ ν ∂ µ A µ = 0. (3.16)□A i − ∂ i (∂ 0 A 0 − ∂ i A i ) = 0. (3.17)∂ i A i = ∇ · ⃗A = 0, (3.18)40

e escolhendo A 0 = 0, conhecida como Calibre Temporal, a equação a ser resolvida se reduzirá à□A i = 0, (3.19)ou seja, a equação da onda, cujo o pontencial vetor A i é solução. Note ainda que ao escolhermoso potencial escalar igual a zero (ϕ = A o = 0), podemos obter o campo E ⃗ através da relaçãoe ⃗ B através de⃗E( ⃗ x, t) = − ∂ ⃗ A∂t = −∂ oA i , (3.20)⃗B(⃗x, t) = ∇ × ⃗ A(⃗x, t) = ɛ ijk ∂ j A k ⃗e i . (3.21)Analogamente ao que foi feito para o campo escalar livre, podemos propor como soluçãopara a equação (3.19), uma equação do tipo∫⃗A(⃗x, t) = dk 3 ⃗ɛ k e i⃗ k·⃗xâk (t), (3.22)sendo ⃗ɛ k o vetor de polarização da onda, que atribui o caráter vetorial para o potencial ⃗ A.Tomando o divergente de (3.22), temos∫∇ · ⃗A = dk 3 ∇ · ⃗ɛ k e i⃗ k·⃗xâk (t),que, em coordenadas cartezianas, se escreverá na forma∫ (∇ · ⃗A = dk 3 î ∂∂x + ĵ ∂ ∂y + ˆk ∂ )· (îɛ x + ĵɛ y +∂zˆkɛ z )e i(kxx+kyy+kzz) â k (t),ou ainda∫∇ · ⃗A =(dk 3 ∂ɛ x∂x + ɛ ∂y∂y + ɛ ∂z∂z)e i(kxx+kyy+kzz) â k (t),que, ao tomarmos as derivadas espaciais da função exponencial, fica∫∇ · ⃗A = dk 3 (ɛ x k x + ɛ y k y + ɛ z k z )e i⃗ k·⃗xâk (t),e ainda∫∇ · ⃗A =dk 3 ⃗ k · ⃗ɛk e i⃗ k·⃗xâk (t).Como, por construção, este potencial vetorial deve satisfazer a escolha de calibre de Coulombdada por (3.18), desta última equação concluimos que⃗ k · ⃗ɛk = 0, (3.23)41

que nos garante que o vetor de polarização é perpendicular ao vetor de onda, e ainda que ocalibre de Coulomb surge como uma condição de transversalidade para o campo. Logo, podemosassociar dois estados de polarização linearmente independentes, ou sejade onde concluimos que⃗ɛ λ k; λ = 1, 2. (3.24)⃗ɛ λ k · ⃗ɛ λ′k = δ λλ ′. (3.25)Assim, já considerando os graus de liberdade para a polarização, teremos que a soluçãogeral para a equação (3.19) será dada, analogamente ao caso do campo escalar, por∫⃗A(⃗x, t) =dk 3√2wk (2π) 32∑⃗ɛ λ k(â kλ e i⃗ k·⃗x−iw k t + â † kλ e−i⃗ k·⃗x+iw k t ), (3.26)λ=1para o qual é válida a relação de dispersão w 2 k = ⃗ k 2 , dada, analagamente ao caso do campoescalar não massivo, por (2.55), fazendo nesta m = 0. Sendo ainda que os operadores de criaçãoe aniquilação satisfazem às seguintes relações de comutação[â † kλ , â k ′ λ ′] = δ λλ ′δ(⃗ k − ⃗ k ′ ),[â kλ , â k ′ λ ′] = 0, (3.27)[â † kλ , ↠k ′ λ ′ ] = 0.Tomando agora o tensor energia-momento dado porθ µν =Substituindo em (3.28) as equações (3.2) e (3.8), esta ficará como∂L∂∂ µ A σ∂ ν A σ − g µν L. (3.28)θ µν = −F µσ ∂ ν A σ + 1 4 gµν F αβ F αβ , (3.29)de onde a componente θ 00 , referente à densidade de energia, é dada porθ 00 = −F 0σ ∂ 0 A σ + 1 4 F αβF αβ . (3.30)De acordo com (3.3), podemos escrever F 0σ = ∂ 0 A σ − ∂ σ A 0 . Como para este calibre estamostrabalhando com A 0 = 0, teremos que F 0σ = ∂ 0 A σ , assim a equação (3.30) ficaθ 00 = 1 4 F αβF αβ − ∂ 0 A σ ∂ 0 A σ .42

Sabemos que os índices α, β e σ variam de 0 a 3, porém, segundo o valor que escolhemos paraA 0 podemos afirmar que as únicas contribuições relevantes para o segundo termo da últimarelação são aquelas calculadas para σ = 1, 2, 3, que não se anularão. Então, de acordo com(3.20), temos queθ 00 = 1 4 F αβF αβ + E ⃗ 2 .Explicitando os termos somados em α no primeiro termo desta última equação, teremosθ 00 = 1 4 (F 0βF 0β + F iβ F iβ ) + E ⃗ 2 ,e ainda para βθ 00 = 1 4 (F 00F 00 + F 0j F 0j + F i0 F i0 + F ij F ij ) + E ⃗ 2 i, j = 1, 2, 3.Como F 00 = F 00 = 0 e observando que os elementos F 0i e F 0i são as componentes do campoelétrico 1 , temos queθ 00 = 1 4 (− E ⃗ 2 − E ⃗ 2 + F ij F ij ) + E ⃗ 2 ,ou aindaθ 00 = 1 E2 ⃗ 2 + 1 4 F ijF ij . (3.31)Note ainda que F ij e F ij são as componentes do vetor indução magnética do tensor deMaxwell. De acordo com (3.3), temosθ 00 = 1 E2 ⃗ 2 + 1 4 (∂ iA j − ∂ j A i )(∂ i A j − ∂ j A i )= 1 E2 ⃗ 2 + 1 4 (∂ iA j ∂ i A j − ∂ i A j ∂ j A i + ∂ j A i ∂ j A i − ∂ j A i ∂ i A j ).Antes de proseguirmos com o cálculo de θ 00 , tomemos o quadrado da equação (3.21), ouseja⃗B 2 = (∇ × A) ⃗ 2 = ɛ ijk ɛ ilm ∂ j A k ∂ l A m ,sendo ɛ ijk e ɛ ilm os tensores de Levi-Civita, que obedecem à propriedadeɛ ijk ɛ ilm = δ jl δ km − δ jm δ kl , (3.32)1 Podemos ratificar tal afirmação conhecendo a forma matricial de tensor F µν , para isso veja o Apêndice Adeste trabaho.43

daí temos que⃗B 2 = (∇ × ⃗ A) 2 = ∂ l A m ∂ l A m − ∂ l A m ∂ m A l .Logo, comparando B ⃗ 2 com a última equação para θ 00 , esta ficará comoθ 00 = 1 2 ( E ⃗ 2 + B ⃗ 2 ), (3.33)com isso o operador Hamiltoniano se escreverá na formaĤ = 1 ∫( E2⃗ 2 + B ⃗ 2 )dx 3 . (3.34)Substituindo (3.26) nas equações (3.20) e (3.21), encontraremos os campos elétricos e ovetor indução magnética, que, já escritos em função de (2.64), são, respectivamente, dados por∫⃗E(⃗x, t) = dk 3e2∑iw k ⃗ɛ λ k(â kλ u k − â † kλ u∗ k) (3.35)λ=1∫ 2∑⃗B(⃗x, t) = dk 3 ik⃗ɛ λ k(â kλ u k − â † kλ u∗ k). (3.36)λ=1Logo substituindo (3.35) e (3.36) em (3.34), temos queĤ = − 1 ∫ ∫ ∫dx 3 dk 32dk ′32∑[⃗ɛ λ k · ⃗ɛ λ′k ′(w kw k ′ + | ⃗ k|| k ⃗′ |)×λ,λ ′ =1×(â kλ â kλ ′u k u k ′ + â † kλ↠kλu ∗ ku ∗ ′ k − ′ ↠kλâkλ ′u∗ ku k ′ − â kλ â † kλu ′ k u ∗ k ′)],que, de acordo com as equações (2.68), (2.69) e (2.70), que relacionam as integrais entre asfunções u k e u ∗ k , ficaĤ = − 1 ∫ dk32 2w k2∑[ɛ λ k · ɛ λ′−k(wk 2 − | ⃗ k| 2 )â kλ â −kλ ′e −2iwkt + ɛ λ k · ɛ λ′−k(wk 2 − | ⃗ k| 2 )â † kλ↠−kλe 2iwkt +′λ,λ ′ =1−ɛ λ k · ɛ λ′k (w 2 k + | ⃗ k| 2 )â † kλâkλ ′ − ɛλ k · ɛ λ′k (w 2 k + | ⃗ k| 2 )â kλ â † kλ ′ ].De acordo com a relação de dispersão wk 2 = |⃗ k| 2 e com (3.25), vemĤ = 1 ∫∑dk 3 w k δ λ,λ ′(â † kλâkλ2′ + â kλ ′↠kλ ),λ,λ ′44

de onde, usando (2.18) e já organizado os termos segundo o produto ordenamento normal, ouseja, arrumando os operadores de criação e aniquilação de tal forma que o primeiro anteceda osegundo, temos∫Ĥ =dk 3 w k2∑â † kλâkλ, (3.37)λ=1que é o operador Hamiltoniano para o caso aqui explorado, ou seja, para o campo eletromagnéticoquantizado segundo o calibre de Coulomb.Podemos ainda observar que ao considerarmos este campo num cubo de volume L 3 , sujeitoa condições de contorno periódicas, teremos uma solução análoga ao caso explorado na secção2.2 deste trabalho, e assim será possível perceber que tal solução terá a forma[13]⃗A(⃗x, t) =∞∑2∑n=−∞ λ=1tendo os devidos cuidados com o vetor de polarização ɛ λ n.ɛ λ n√ 2wk L 3 (â nλe i⃗ k·⃗x−iw nt + â † nλ e−i⃗ k·⃗x+iw nt ) (3.38)3.3 A Quantização do Campo Eletromagnético via Calibrede LorentzTomando novamente para este caso a densidade de Lagrangeana dada pela equação (3.2),onde o momento canonicamente conjugado ao campo A µ é dado porπ µ =∂L∂∂ 0 A µ= −F 0µ , (3.39)podemos perceber que a componente temporal deste será nula (π 0 = 0). De onde concluimosque o fato da densidade de Lagrangeana não depender explicitamente de ∂ 0 A 0 nos leva a umaaparente inconsistência que, à princípio, nos impede de procedermos com o processo de quatizaçãocanônica neste calibre, pois com isto estamos afirmando que A 0 não possui um momentocanonicamente cojugado a ele. Uma primeira tentativa de contornarmos tal resultado seria considerarA 0 = 0 (o que foi feito na secção anterior), porém como no formalismo covariante todasas componentes de A µ devem ser tratadas no mesmo “pé de igualdade”, tal feito se tornainconsistente com nossa proposta, a de quantização covariante.Para nos mantermos consistentes, faremos uso de uma sugestão dada por Fermi que consistebasicamente numa densidade de Lagrangeana modificada dada por[8]L = − 1 4 F µνF µν − 1 2 ξ(∂ αA α ) 2 , (3.40)45

onde ξ é um parâmetro que pode assumir valores inteitos.Esta equação deve ainda nos levar à resultados que concordem com a teoria clássica paraeste calibre, o que nos leva à concluir quequando impomos o calibre de Lorentz, dado porna equação (3.16).□A µ = 0, (3.41)∂ µ A µ = 0, (3.42)Substituindo a equação (3.40) na equação de Euler-Lagrange dada por (3.5), teremos quecalcular, basicamente, derivadas do segundo termo da equação (3.40) uma vez que as derivadasdo primeiro termo já foram calculadas anteriormente na secção 3.1, logo calculando cada termoda equação de Euler-Lagrange, temos∂L= − 1 ∂(F µν F µν ) − 1 ∂A γ 4 ∂A γ 2 ξ ∂ (∂ α A α ) 2 = 0, (3.43)∂A γuma vez que na densidade de lagrangeana, dada por (3.40), não há dependência explícita docampo A µ , mas sim de suas derivadas.O outro termo da equação de Euler-Lagrange nos leva a∂L= − 1 ∂(F µν F µν ) − 1 ∂∂ β A γ 4 ∂∂ β A γ 2 ξ ∂(∂ α A α ) 2 .∂∂ β A γO primeiro termo desta também já foi devidamente calculada na secção 3.1. Já para o segundotermo, introduziremos o tensor métrico com o objetivo de baixar o índice do termo que seráderivado e proseguiremos com a operação naturalmente, assim, temos, utilizando também (3.7),quePortanto∂L∂∂ β A γ= −F βγ − 1 2 ξ ∂∂∂ β A γ(g αρ ∂ α A ρ ) 2∂ β= −F βγ − g βγ ξ∂ α A α .Então a equação de Euler-Lagrange ficará como∂L= −∂ β F βγ − ξ∂ γ ∂ α A α . (3.44)∂∂ β A γ∂ β F βγ + ξ∂ γ ∂ α A α = 0,46

ou ainda, em termos de (3.3), como∂ β (∂ β A γ − ∂ γ A α ) + ξ∂ γ ∂ α A α = 0.Já que estamos trabalhando com índices mudos, podemos escrever esta última equação naforma□A µ − (1 − ξ)∂ µ ∂ α A α = 0. (3.45)Note ainda que, através da equação (3.39), podemos mostrar que o momento canonicamenteconjugado ao campo seráπ µ = −F 0µ − ξg 0µ ∂ α A α , (3.46)cujas componentes espaciais são dadas porπ i = ∂ i A 0 − ∂ 0 A i , (3.47)e a temporal porπ 0 = −ξ∂ α A α , (3.48)ambos diferente de zero, conforme nosso intuito.Embora a equação (3.40) seja válida para todo valor inteiro de ξ, para simplificarmos oscálculos escolheremos ξ = 1, tal escolha é conhecida como calibre de Feynman ou de Fermi,com isso percebemos que o operador de campo em questão satisfaz a equação da onda, ou seja,□µ = 0, (3.49)cuja solução, análoga ao calibre de Coulomb, apresenta quatro estados de polarização linearmenteindependentes: λ = 0 relativa à uma polarização do tipo tempo e λ = 1, 2 e 3 relativas àspolarizações espaciais, sendo que λ = 1 e 2 dizem respeio aos estados de polarização transversaise λ = 3 ao estado de polarização longitudinal, de acordo com nossa escolha de base.Logo, analogamente ao resultado apresentado em (3.26), temos que∫ 3∑ µ (⃗x, t) = dk 3 ɛ µ (k, λ)(â † kλ u k + â kλ u ∗ k). (3.50)λ=0Efetivando o processo canônico de quantização teremos que o campo em questão satisfaráàs seguintes relações de comutação para tempos iguais, de forma análoga ao que fizemos em(1.65), segundo o princípio da correspondência[µ (⃗x, t), ˆπ ν (⃗y, t)] = ig µν δ 3 (⃗x − ⃗y),47

[µ (⃗x, t), Âν (⃗y, t)] = 0, (3.51)sendo que, segundo a relação (1.30), temos∫ˆπ µ (⃗x, t) = i[ˆπ µ (⃗x, t), ˆπ ν (⃗y, t)] = 0,dk 3 w k3∑ɛ µ (k, λ)(â † kλ u k − â kλ u ∗ k). (3.52)λ=0Note nas equações (3.50) e (3.52) a presença de quadri-vetores de polarização ɛ µ (k, λ) quesatisfazem a relação dada porɛ µ (k, λ)ɛ µ (k, λ ′ ) = g λλ ′, (3.53)ou seja, os vetores de polarização formam um sistema ortonormal quadri-dimensional.3.4 O Calibre de Lorentz e o Método de Gupta-BleulerCalculando a relação de comutação entre o operador campo µ e o operador ∂ µ  µ temos[∂ µ  µ (⃗x, t), Âν (⃗y, t)] = [∂ 0  0 + ∂ i  i , Âν (⃗y, t)],ou ainda, segundo a propriedade [ + ˆB, Ĉ] = [Â, ˆB] + [ ˆB, Ĉ][19], reescrevemos esta últimacomo[∂ µ  µ (⃗x, t), Âν (⃗y, t)] = −[ˆπ 0 (⃗x, t), Âν (⃗y, t)] + ∂ i [Âi (⃗x, t), Âν (⃗y, t)],e levando em conta as relações dadas por (3.51), temos que[∂ µ  µ (⃗x, t), Âν (⃗y, t)] = ig ν0 δ 3 (⃗x − ⃗y) ≠ 0. (3.54)Note que para que a relação de comutação calculada anteriormente fosse nula, ou o operador∂ µ A µ (⃗x, t) teria que ser nulo ou este teria que comutar com A µ (⃗x, t). Como, segundo o resultadoencontrado acima, ambos os operadores não comutam e como estamos lidando com um campoA µ (⃗x, t) ≠ 0, este resultado nos faz concluir que o operador de campo não satisfaz o calibre deLorentz como no caso clássico, ou seja,∂ µ  µ ≠ 0, (3.55)de maneira que possa se dizer que o processo de quantização canônica não é compatível como calibre de Lorentz. A solução dessa incongruência será discutida posteriormente, por horavejamos em que a escolha desse calibre implica, à princípio, para o operador Hamiltoniano.48

Para encontrarmos o operador hamiltoniano nos é conveniente reescrevermos a equação(3.40) já levando em consideração o valor unitário para o parâmetro ξ. Escrevendo este emtermos de (3.3), temosL = − 1 4 (∂ µA ν − ∂ ν A µ )(∂ µ A ν − ∂ ν A µ ) − 1 2 (∂ αA α ) 2 ,que, ao multiplicarmos os termos, ficaL = − 1 4 (∂ µA ν ∂ µ A ν − ∂ µ A ν ∂ ν A µ − ∂ ν A µ ∂ µ A ν + ∂ ν A µ ∂ ν A µ ) − 1 2 (∂ αA α ) 2 .Nesta última relação, note, dentro dos primeiros parênteses, que alguns termos se assemelham,como estamos trabalhando com índices mudos, podemos agrupar estes de tal forma que aLagrangeana pode ser escrita comoL = − 1 2 ∂ µA ν ∂ µ A ν + 1 2 ∂ µA ν ∂ ν A µ − 1 2 ∂ µA µ ∂ ν A ν , (3.56)sendo ∂ µ A µ ∂ ν A ν = (∂ α A α ) 2 , escrita de tal forma que explicite os fatores envolvidos no produtoem questão.Com o intuito de reescrevermos os dois primeiros termos da equação (3.56), calcularemos aderivada ∂ µ [A ν (∂ ν A µ ) − (∂ ν A ν )A µ ], que segundo a regra do produto, dar-se-à por∂ µ [A ν (∂ ν A µ ) − (∂ ν A ν )A µ ] = ∂ µ A ν ∂ ν A µ + A ν (∂ ν ∂ µ A µ ) − (∂ µ ∂ ν A ν )A µ − ∂ ν A ν ∂ µ A µ ,usando o tensor métrico, baixaremos alguns índices do segundo e do terceiro termo do resultadoacima, com isso∂ µ [A ν (∂ ν A µ ) − (∂ ν A ν )A µ ] = ∂ µ A ν ∂ ν A µ − ∂ ν A ν ∂ µ A µ + g νρ A ν (∂ ρ ∂ µ A µ ) − g µσ A σ (∂ µ ∂ ν A ν ),observe que os últimos termos se cancelam, logo∂ µ [A ν (∂ ν A µ ) − (∂ ν A ν )A µ ] = ∂ µ A ν ∂ ν A µ − ∂ µ A µ ∂ ν A ν .Desta forma, (3.56) poderá ser reescrita comoL = − 1 2 ∂ µA ν ∂ µ A ν + 1 2 ∂ µ[A ν (∂ ν A µ ) − (∂ ν A ν )A µ ].Sendo o segundo termo a quadri-divergência que, por sua vez, não dará contribuição para nossospropósitos, pois com o uso do Teorema de Gauss, podemos escolher uma superfície na qual ocampo se anule. Como estamos trabalhando com o campo livre, tal superfície se encontra noinfinito, portanto a densidade de Lagrangeana que dará contribuição será apenasL = − 1 2 ∂ µA ν ∂ µ A ν . (3.57)49

Logo, de forma análoga aos cálculos já efetuados para o campo escalar e para o campoeletromagnético via calibre de Coulomb a densidade de energia, partindo-se de (3.28) para opresente caso, será dada porθ 00 = −π µ π µ + 1 2 ∂ µA ν ∂ µ A ν .Explicitando as componentes temporais e espaciais de ∂ µ , teremosθ 00 = −π µ π µ + 1 2 ∂ 0A ν ∂ 0 A ν + 1 2 ∂ jA ν ∂ j A ν ,que, segundo a definição do momento canonicamente conjugado (1.30) e o fato de que ∂ j = −∂ j ,ficaou ainda,θ 00 = −π µ π µ + 1 2 πµ π µ − 1 2 ∂ jA ν ∂ j A ν ,θ 00 = − 1 2 πµ π µ − 1 2 ∂ jA ν ∂ j A ν .Aplicando a derivado ∂ j no campo (3.50) teremos, já em termos das funções u k , que∫∂ j A µ = idk 3 k3∑ɛ µ (k, λ)(â kλ u k − â † kλ u∗ k). (3.58)λ=0Analogamente ao que já foi visto na secção anterior, para a obtenção do operador hamiltoniano,partindo de uma relação similar à (2.66) e com o auxílio das relações (2.68), (2.69) e(2.70) podemos mostrar queĤ = − 1 2∫dk 3 w k3∑λ,λ ′ =0que de acordo com (3.53) ficará comoĤ = − 1 2∫dk 3 w kɛ µ (k, λ)ɛ µ (k, λ ′ )(â † kλâkλ ′ + â kλâ † kλ ′ ), (3.59)3∑λ,λ ′ =0g λλ ′(â † kλâkλ ′ + â kλâ † kλ ′ ). (3.60)Como as únicas contribuições relevantes para esta última dar-se-ão para λ = λ ′ , correspondendoà diagonal principal do tensor métrico, e já impondo sobre esta o ordenamento normal,concluímos que∫Ĥ =dk 3 w k3∑(−g λλ )â † kλâkλ, (3.61)λ,λ ′ =050

ou ainda, explicitando a somatória, temos∫Ĥ = dk 3 w k (−â † k0âk0 + â † k1âk1 + â † k2âk2 + â † k3âk3), (3.62)de maneira que é possível notar que para este caso os operadores de criação e aniquilação criame aniquilam fotóns relativos a quatro diferentes tipos de polarização, sendo que a polarizaçãodo tipo tempo traz um problema de norma negativa que analizaremos a partir de agora.Analogamente ao caso discreto, ondeâ kλ |0〉 = 0; ∀ k, λ, (3.63)e ainda|n kλ 〉 = (↠kλ )n kλ√nkλ !|0〉 , (3.64)de onde vemos que para criarmos, a partir do vácuo, um único fóton, devemos ter|1 kλ 〉 = â † kλ|0〉 . (3.65)A última relação pode ser escrita, tomando o limite para o contínuo, como∫|1 kλ 〉 = dk ′3 F k (k ′ )â † k ′ λ|0〉 (3.66)sendo F k (k ′ ) uma função “distribuição de densidade” que descreve o quão próximos estão osvários estados possíveis para criação ou aniquilação de partículas (fóton) com número de ondak. Tal função obedece ainda a relação[6]∫dk ′3 |F k (k ′ )| 2 = 1. (3.67)Para encontrarmos a norma do estado dado por (3.66), devemos fazer∫ ∫〈1 kλ |1 kλ 〉 = dk ′3 dk ′′3 F k (k ′ )F k (k ′′ ) 〈0| â k ′ λâ † k ′′ λ|0〉 (3.68)que de acordo com[â † kλ , â k ′ λ ′] = g λλ ′δ(⃗ k − ⃗ k ′ ),[â kλ , â k ′ λ ′] = 0, (3.69)[â † kλ , ↠k ′ λ ′ ] = 0,51

que nos dá as relações de comutação entre os operadores de criação e aniquilação para o casoaqui explorado[9]. Mais especificamente de acordo com o primeiro comutador deste últimoconjunto de equações, temos que (3.68) pode ser escrita como∫ ∫〈1 kλ |1 kλ 〉 = dk ′3 dk ′′3 F k (k ′ )F k (k ′′ ) 〈0| (â † k ′ λâk ′′ λ − g λλ )δ 3 ( ⃗ k ′ , ⃗ k ′′ ) |0〉 ,como o valor esperado 〈0| â † k ′ λâk ′′ λ |0〉 = 0 segundo (3.63), teremos∫ ∫〈1 kλ |1 kλ 〉 = dk ′3 dk ′′3 F k (k ′ )F k (k ′′ ) 〈0| − g λλ δ 3 ( ⃗ k ′ , ⃗ k ′′ ) |0〉 ,que concordando com (2.18), fica〈1 kλ |1 kλ 〉 = −g λλ∫dk ′3 |F k (k ′ )| 2 〈0|0〉 ,que de acordo com (3.67), temos, finalmente, que〈1 kλ |1 kλ 〉 = −g λλ , (3.70)na qual percebemos que a norma para o estado de 1 único fóton, em λ = 0, é negativa, o queimpossibilita uma interpretação probabilística para a teoria, interpretação essa, fundamentalpara a física quântica. Tal resultado nos conduz ainda a um valor de energia negativa para oestado de polarização referênte a λ = 0 no quadi-vetor de polarização ɛ µ (k, λ).Com o intuito de contornarmos esse problema, voltemos à impossibilidade do calibre deLorentz dada pela equação (3.56), para esta, afirmaremos que num sub-espaço do espaço deHilbert, representado por |ψ〉, o valor esperado da equação (3.56) satisfará o calibre de Lorentz,logo〈ψ| ∂ µ  µ |ψ〉 = 0, (3.71)ou seja, o valor médio de ∂ µ  µ deverá ser nulo quando calculado neste sub-espaço.Escrevendo o operador de campo, por simplicidade, como µ (⃗x, t) = µ(+) (⃗x, t) + µ(−) (⃗x, t), (3.72)onde µ(+) (⃗x, t) e µ(−) (⃗x, t) estão relacionados, respectivamente, aos operadores de aniquilaçãoe criação, sendo ainda que[µ(+) ] † = µ(−) . (3.73)Ao impormos a relação matemática∂ µ  µ(+) |ψ〉 = 0, (3.74)52

que por sua vez terá como correspondente dual a equaçãopodemos, enfim, escrever que〈ψ| ∂ µ  µ(−) = 0, (3.75)〈ψ| ∂ µ  µ |ψ〉 = 〈ψ| ∂ µ  (+) |ψ〉 + 〈ψ| ∂ µ  (−) |ψ〉 = 0. (3.76)A equação (3.74), que garante a última igualdade, é a chamada condição de Gupta-Bleuler. Outra importante observação que podemos fazer à respeito desta condição pode serobtida explicitando esta, ou seja∫dk 3√2wk (2π) 3 eiw kt−i ⃗ k·⃗x3∑k µ ɛ µ (k, λ)â kλ |ψ〉 = 0, (3.77)que explicitando os termos da somatória, fica∫dk 3√2wk (2π) 3 eiw kt−i ⃗k·⃗x [k µ ɛ µ (k, 0) + k µ ɛ µ (k, 1) + k µ ɛ µ (k, 2) + k µ ɛ µ (k, 3)] |ψ〉 = 0.λ=0Como, para este caso, k µ ɛ µ (k, 1) = k µ ɛ µ (k, 2) = 0 e ainda k µ ɛ µ (k, 0) = −k µ ɛ µ (k, 3) [9], temos∫dk 3√2wk (2π) 3 eiw kt−i ⃗k·⃗x k µ ɛ µ (k, 0)(â k0 − â k3 ) |ψ〉 = 0. (3.78)Veja que para que a relação acima seja de fato nula, temos que garantir quecuja correspondente dual é dada porˆL k |ψ〉 = (â k0 − â k3 ) |ψ〉 = 0, (3.79)〈ψ| ˆL † k = 〈ψ| (↠k0 − ↠k3) = 0, (3.80)que representa uma relação entre os fóton relativos à polarização escalar λ = 0 e os fótonrelativos à polarização longitudinal λ = 3, de onde podemos concluir ainda queâ k0 |ψ〉 = â k3 |ψ〉〈ψ| â † k0 = 〈ψ| ↠k3 , (3.81)o que nos remete, tomando o produto escalar entre as relações contidas em (3.81), ao resultado〈ψ| â † k0âk0 |ψ〉 = 〈ψ| â † k3âk3 |ψ〉 . (3.82)Com isso, ao calcularmos, por fim, o valor esperado para o operador Hamiltoniano dado por(3.63), encontramos que〈Ĥ〉 ∫= dk 3 w k 〈ψ| (−â † k0âk0 + â † k1âk1 + â † k2âk2 + â † k3âk3) |ψ〉 ,53

ou ainda, de acordo com (3.79), que〈Ĥ〉 ∫=2∑dk 3 w k 〈ψ| â † kλâkλ |ψ〉 ,λ=1que tem basicamente a forma∫Ĥ =dk 3 w k2∑ˆN kλ , (3.83)λ=1sendo ˆN kλ o operador numeral já definido por nós anteriormente em (2.34).Com o desenvolvimento que viemos fazendo desde (3.61) até a equação (3.83), com o auxíliodo método de Gupta-Bleuler dado por (3.74), nos foi possível perceber que os estados depolarização logitudinal e escalar não contribuem para o calculo da energia, o que é consistentecom medidas experimentais onde apenas fótons transversais são observados. Estes estados, osde polarizações logitudinal e escalar, surgem unicamente do desenvolvimento matemático queseguimos, sendo descartados por argumentos físicos no decorrer da teoria.54

Capítulo 4A Quantização do Campo VetorialMassivoPara uma melhor descrição das interações fracas é de grande importância um melhor entendimentoda física que rege o campo vetorial massivo, também conhecidos como campo deProca. A quantização deste tipo de campo será alvo de nosso estudo neste capítulo fazendoalgumas comparações com o caso estudado no capítulo anterior onde a massa do campo vetorial(campo eletromagnético) era tida como nula.4.1 As Equações de ProcaJá considerando nula as distribuições de cargas e correntes, a densidade de Lagrangeanaque descreve um campo vetorial massivo é dada por[8][9]L = − 1 4 F µνF µν + 1 2 m2 A µ A µ (4.1)sendo A µ um campo real e neutro, F µν o tensor de Maxwell já apresentado no capítulo anteriore m a massa da partícula mediadora desta interação.Substituindo a Lagrangeana (4.1) na equação de Euler-Langrage, equação (3.5), e calculandocada termo desta, teremos, já utilizando o tensor métrico, que o primeiro será(∂m 2 1 )∂A σ 2 A µA µ = m 2 1 ∂(g µρ A µ A ρ ),2 ∂A σno qual podemos notar que para o cálculo do primeiro termo da equação de Euler-Lagrangedada por (3.5) só será relevante o segundo termo de (4.1), uma vez que o primeiro desta nãoapresenta dependencia explicita dos campos A µ , e sim, segundo (3.3), apenas de suas derivadas.Assim sendo, segundo a regra da derivada do produto e recordando que ∂Aµ∂A ν= δ µν , a última55

equação pode ser escrita como(∂m 2 1 )∂A σ 2 A µA µ = m 2 1 2 (gµρ δ µσ A ρ + g µρ δ ρσ A µ ),que, por fim, utilizando a propriedade do tensor métrico e da Delta, temos(∂m 2 1 )∂A σ 2 A µA µ = m 2 A σ ,que é o primeiro termo da Equação de Euler-Lagrange.Para o segundo termo da Equação de Euler-Lagrange teremos que calcular, basicamente, aderivada do primeiro termo de (4.1), uma vez que somente este apresenta dependência explicitadas derivadas do campo A µ . Assim sendo, para este cálculo podemos utilizar um resultado jácalculado anteriormente em (3.9).Logo, reunindo o resultado de (3.9) com o resultado encontrado na última equação acima,temos que a equação de movimento para o campo A µ é dada porou, em termos explicitos do campo, segundo (3.3), como∂ µ F µν + m 2 A ν = 0, (4.2)□A ν − ∂ ν (∂ µ A µ ) + m 2 A ν = 0, (4.3)que são as chamadas Equações de Proca, equações que regem a dinâmica do campo vetorialmassivo.Tomando a quadri-divergência ∂ ν da equação (4.3) e de acordo com (2.6), temos∂ µ ∂ µ ∂ ν A ν − ∂ ν ∂ ν (∂ µ A µ ) + m 2 ∂ ν A ν = 0,e lembrando que µ e ν são índices mudos podemos perceber os dois primeiros termos da últimaequação se cancelam mutuamente, e desta forma temosm 2 ∂ ν A ν = 0.Uma vez que m 2 ≠ 0 concluimos finalmente que∂ ν A ν = 0. (4.4)Desta forma notamos que, contrariamente ao campo eletromagnético, o campo de Proca satisfazde maneira imediata a condição de Lorentz, o que nos permite reescrever a equação (4.3)simplesmente como(□ + m 2 )A ν = 0, (4.5)56

ou seja, todas as componentes de A µ satisfazem a equação homogênea de Klein-Gordon. Comisso percebemos que a solução da equação (4.5) pode ser obtida de maneira análoga ao que jávinhamos fazendo até então, salvo algumas observações que serão destacadas no decorrer destecapítulo.4.2 A Quantização do Campo de ProcaPara darmos início ao processo de quantização do campo Proca comecemos por encontraro momento canonicamente conjugado a este, que será dado, de acordo com (3.39), porπ µ = −F 0µ . (4.6)Segundo a forma matricial do tensor de Maxwell (veja apêndice A), podemos notar que ascomponentes temporais e espaciais de (4.6) são dadas, respectivamente, porπ 0 = 0π i = E i .(4.7)Neste ponto, assim como no capítulo anterior, vale ressaltar que a componente temporal docampo não possui um momento canonicamente conjugado a ele, não sendo possível, portanto,apresentar uma relação de comutação entre essas grandezas. Porém, neste caso, podemos darconta do campo A 0 usando as equações de movimento que o campo satisfaz, ou seja, a variaçãode A 0 será regulada por essas equações, que, quando calculadas de acordo com a equação (4.2)para ν = 0, temos queA 0 = − 1 m ∂ iE i . (4.8)2Sendo assim, seguindo o protocolo da quantização canônica, podemos impor as regras decomutação para tempos iguais entre os observáveis, dadas por[Âi (⃗x, t), ˆπ j (⃗y, t)] = [Âi (⃗x, t), Êj (⃗y, t)] = iδ ij δ 3 (⃗x − ⃗y),[Âi (⃗x, t), Âj (⃗y, t)] = 0, (4.9)[ˆπ i (⃗x, t), ˆπ j (⃗y, t)] = [Êi (⃗x, t), Êj (⃗y, t)] = 0,e promover a variável dinâmica, descrita pela equação (4.8), para a categoria de operador, demaneira que podemos escrever 0 = − 1 m ∂ 2 iÊi . (4.10)57

Para as quantidades Âi e Â0 , usando a equação anterior para Â0 , temos ainda a seguinte relaçãode comutação[Âi (⃗x, t), Â0 (⃗y, t)] =[ i (⃗x, t), − 1 ]m ∂ 2 jÊj (⃗y, t) ,e como a derivada ∂ j é em relação a ⃗y ela pode ser retirada de dentro do comutador, assimcomo o termo − 1 m 2 , sendo possível escrever a equação anterior simplesmente como[Âi (⃗x, t), Â0 (⃗y, t)] = − 1 m 2 ∂ j[Âi (⃗x, t), Êj (⃗y, t)],que, usando a primeira das relações (4.9), fica[Âi (⃗x, t), Â0 (⃗y, t)] = − 1 m 2 ∂ iδ 3 (⃗x − ⃗y), (4.11)e ainda para as relações entre campos Â0 , calculados em tempos iguais, temos finalmente[Â0 (⃗x, t), Â0 (⃗y, t)] = 0. (4.12)Note nestas últimas relações que as componentes do campo A µ são tratadas separadamente,não mantendo assim a idéia de covariância, uma vez que as componentes espaciais e temporaisdo campo de Proca foram separadamente quantizadas.Com o intuito de contornarmos talincongruência é necessário redefinir algumas das relações de comutação já explicitadas.Porém, antes disso, é conveniente escrevermos a solução geral da equação de movimento(4.5) que, de acordo com a decomposição em ondas planas e já considerando apenas os trêsgraus de liberdade das variáveis dinâmicas independentes, será dada por∫ µ (⃗x, t) =dk 33∑ɛ µ (k, λ)(â kλ u k + â † kλ u∗ k), (4.13)λ=1ou, explicitando as funções u k , dadas por (2.64), podemos ainda escreve tal solução comosendo∫ µ (x µ ) =dk 3√2wk (2π) 33∑ɛ µ (k, λ)(â kλ e −ikµxµ + â † kλ eikµxµ ), (4.14)λ=1k µ = (k 0 , ⃗ k),x µ = (t = x 0 , ⃗x),k µ x µ = w k t − ⃗ k · ⃗x,(4.15)tendo as três bases de polarização definidas convenientemente por[9] (Veja Apêndice B)ɛ µ (k, 1) = (0,⃗ɛ(k, 1)),58

ɛ µ (k, 2) = (0,⃗ɛ(k, 2)), (4.16)ɛ µ (k, 3) =( ) |k|m , k k 0.|k| mConsideremos agora, diferentemente do que vinhamos fazendo até então, a relação de comutaçãoentre os campos µ (x µ ) e µ (y µ ) não apenas em pontos, mas também em temposdiferentes. Daí virá, utilizando (4.14), que∫[µ (x µ ), µ (y µ )] =dk 3 ∫√2wk (2π) 3dk ′3√2w′k(2π) 33∑λ,λ=1ɛ µ (k, λ)ɛ ν (k ′ , λ ′ )[(â kλ e −ikµxµ + â † kλ eikµxµ )××(â k ′ λ ′e−ik′ µy µ + â † k ′ λ ′ e ik′ µy µ ) − (â k ′ λ ′e−ik′ µy µ + â † k ′ λ ′ e ik′ µy µ )(â kλ e −ikµxµ + â † kλ eikµxµ )].Efetuando os produtos explicitados acima podemos identificar neste resultado algumas relaçõesde comutação para os operadores de criação e aniquilação. Desta maneira a última equaçãopode ser escrita como∫[µ (x µ ), µ (y µ )] =dk 3 ∫√2wk (2π) 3dk ′3√2w′k(2π) 33∑λ,λ=1ɛ µ (k, λ)ɛ ν (k ′ , λ ′ ){[â kλ , â k ′ λ ′]e−i(kµxµ +k ′ µ yµ) ++[â kλ , â † k ′ λ ′ ]e −i(kµxµ −k ′ µ yµ) + [â † kλ , â k ′ λ ′]ei(kµyµ −k ′ µ yµ) + [â † kλ , ↠k ′ λ ′ ]e i(kµxµ +k ′ µ yµ) },que, de acordo com as relações de comutação para os operadores de criação e aniquilação dadaspor (3.69), a relação de comutação entre os campos µ (x µ ) e µ (y µ ) fica∫[µ (x µ ), µ (y µ )] =dk 3 ∫√2wk (2π) 3dk ′3√2w′k(2π) 33∑λ,λ=1g λλ ′δ 3 ( ⃗ k − ⃗ k ′ )××ɛ µ (k, λ)ɛ ν (k ′ , λ ′ )[e i(kµxµ −k ′ µy µ) − e −i(kµxµ −k ′ µy µ) ].Segundo (2.18) e como as únicas contribuições não nulas para a última igualdade dar-se-ão paraλ = λ ′ , em virtude da diagonal principal do tensor métrico, teremos que∫[µ (x µ ), µ (y µ )] = −dk 32w k (2π) 33∑ɛ µ (k, λ)ɛ ν (k, λ)[e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ].Como para o caso do campo de Proca temos que[9] (Veja Apêndice B)3∑λ=1λ=1ɛ µ (k, λ)ɛ ν (k, λ) = −(g µν − 1 )m 2 kµ k ν , (4.17)59

e o comutador que estamos calculando terá a forma∫ ([µ (x µ ), µ (y µ dk 3)] = −−g µν + 1 )2w k (2π) 3 m 2 kµ k ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ].É possivel reescrever esta última relação de comutação de tal maneira que o integrandodesta seja composto apenas das exponênciais nesta existentes. Para tanto vamos resolver aderivada ∂ µ ∂ ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ] e, já utilizando o tensor métrico, temos∂ µ ∂ ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ] = g µβ g νρ ∂ β ∂ ρ [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ],que ao aplicarmos a primeira derivada, em ∂ ρ , fica∂ µ ∂ ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ] = g µβ g νρ ∂ β [ik µ∂x µna qual ∂xµ∂x β∂x β eikµ(xµ −y µ) + ik µ∂x µ∂x β e−ikµ(xµ −y µ) ],= δ µ β. Segundo a propriedade de filtragem da Delta, a última relação fica∂ µ ∂ ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ] = g µβ g νρ ∂ β [ik β e ikµ(xµ −y µ) + ik β e −ikµ(xµ −y µ) ].Aplicando agora a derivada ∂ β de forma analoga ao que fizemos para a derivada ∂ ρ , teremos∂ µ ∂ ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ] = −g µβ g νρ [k β k ρ e ikµ(xµ −y µ) − k β k ρ e −ikµ(xµ −y µ) ],desta forma, colocando k β e k ρ em evidência e levantando seus índices com o auxílio do tensormétrico, temos a igualdade∂ µ ∂ ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ] = −k µ k ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ].Logo, usando a expressão acima na relação de comutação [µ (x µ ), µ (y µ )], que vinhamos calculando,obtemos que∫[µ (x µ ), µ (y µ )] = −ou ainda[µ (x µ ), µ (y µ )] =(g µν + 1 ) ∫m 2 ∂µ ∂ νSabendo que[20](dk 3−g µν − 1 )2w k (2π) 3 m 2 ∂µ ∂ ν [e ikµ(xµ −y µ) − e −ikµ(xµ −y µ) ],dk 32w k (2π) 3 [eikµ(xµ −y µ) − e −ikµ(xµ −y µ) ].sin θ = eiθ − e −iθ, (4.18)2ia nossa relação de comutação ficará[µ (x µ ), µ (y µ )] = i(g µν + 1 ) ∫ dkm 2 ∂µ ∂ ν 3sin k µ (x µ − y µ ).(2π) 3 w k60

Introduziremos agora a chamada Função de Pauli-Jordan definida como[9]∫ dk∆(x µ − y µ 3sin k µ (x µ − y µ )) = −. (4.19)(2π) 3 w kConcluímos então que o comutador [µ (x µ ), µ (y µ )] pode ser escrito na forma[µ (x µ ), µ (y µ )] = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆(x µ − y µ ). (4.20)A função de Pauli-Jordan obedece à algumas importantes propriedades, tais como:É impar no argumentoÉ nula quando calculada em tempos iguais, ou seja,∆(x µ − y µ ) = −∆(y µ − x µ ). (4.21)∆(x µ − y µ )| x0 =y 0= 0. (4.22)Sua primeira derivada temporal calculada em tempos iguais é dada por∂ 0 ∆(x µ − y µ )| x0 =y 0= −δ 3 (⃗x − ⃗y). (4.23)É solução da equação homogênea de Klein-Gordon, logo(□ + m 2 )∆(x µ − y µ ) = 0. (4.24)Então, de acordo com a equação (4.20), percebemos que o processo de quantização tambémé covariante para campos vetoriais massivos, uma vez que a função de Pauli-Jordan é uminvariante de Loretz[8][9]. E ainda, de acordo com as propriedades da função de Pauli-Jordanpodemos perceber que as relações (4.9), (4.11) e (4.12) são casos especiais que surgem demaneira imediata da relação de comutação covariante dada por (4.20), quando consideramosesta para tempos iguais. Esta mesma consideração, para as relações de comutação, pode serfeita para outros campos, como o campo escalar e o campo de Maxwell, por exemplo. Diantedisto podemos escrever uma relação de comutação para campos escalares[8][9] dada agora naforma[ ˆϕ(x µ ), ˆϕ(y µ )] = i∆(x µ − y µ ), (4.25)e para o campo eletromagnético[9], no calibre de Lorentz, como[µ (x µ ), Âν (y µ )] = −ig µν D(x µ − y µ ), (4.26)61

sendo que D(x µ − y µ ) é a própria função de Pauli-Jordan, com a ressalva de que aqui ela estádefinida para campos vetoriais cuja massa é nula, por isso, por questão de notação trocamos ∆por D. E no calibre de Coulomb teremos[Âi (x µ ), Âj (y µ )] = iP ij⊥ D(xµ − y µ ), (4.27)na qual( )P ij⊥ = δ ij − ∂i ∂ j, (4.28)∇ 2que é o denominado Operador Projeção Transversa[9].Para obter agora a relação de comutação entre os operadores Âν (y ν ) e suas derivadas, ouseja, entre ∂ µ  µ (x µ ) e Âν (y ν ), teremos simplesmente que calcularque de acordo com (4.20), fica[∂ µ  µ (x µ ), Âν (y ν )] = ∂ µ [µ (x µ ), Âν (y ν )],[∂ µ  µ (x µ ), Âν (y ν )] = −i∂ µ(g µν + 1 m 2 ∂µ ∂ ν )∆(x µ − y µ ).Introduzindo a derivada ∂ µ no parêntese e levantando seu índice graças ao tensor métrico, temos[∂ µ  µ (x µ ), Âν (y ν )] = −i(∂ ν + 1 )m ∂ µ∂ µ ∂ ν ∆(x µ − y µ ),2que ao identificarmos nesta o D’Lambertiano, dado por ∂ µ ∂ µ , e colocando 1 m 2 ∂ ν em evidência,ficaremos com[∂ µ  µ (x µ ), Âν (y ν )] = − im 2 ∂ν (□ + m 2 )∆(x µ − y µ ),que de acordo com (4.24) fica, finalmente, na forma[∂ µ  µ (x µ ), Âν (y ν )] = 0.Como Âν (y ν ) ≠ 0, de acordo com a última relação nota-se que faz sentido que ∂ µ  µ (x µ ) = 0,ou seja, diferentemente do campo eletromagnético explorado na secção 3.3, o campo de Procasatisfaz de maneira imediata a condição de Lorentz, dada por (3.42), uma vez que a função dePauli-Jordan satisfaz a equação homogênea de Klein-Gordon dada por (4.24).Como no momento a nossa intenção é encontrar o operador Hamiltoniano, partiremos novamenteda componente θ 00 do tensor energia-momento, dado porθ 00 =∂L∂∂ 0 A µ∂ 0 A µ − L.62

O primeiro termo desta última equação pode ser reescrito de acordo com a equação (3.39) e osegundo termo de acordo com a equação (4.1), desta maneira, temosθ 00 = −F 0µ ∂ 0 A µ + 1 4 F µνF µν − 1 2 m2 A µ A µ ,que, explicitando a somatória contida nos dois primeiros termos e efetuando o produto doterceiro termo, temosθ 00 = −F 0i ∂ 0 A i + 1 4 (F 0jF 0j + F 0i F 0i + F ij F ij ) − 1 2 m2 (A 2 0 − ⃗ A 2 ),e já que F 00 = F 00 = 0, e sabendo ainda que F 0i e F 0i são as componentes do campo elétrico,temos queθ 00 = − ⃗ E · ∂ 0 A i + 1 4 (−2 ⃗ E + F ij F ij ) − 1 2 m2 (A 2 0 − ⃗ A 2 ).Note nos resultados (3.31) e (4.32), bem como nos cálculos efetuados entre essas duas equações,que F ij F ij representam o vetor indução magnética, que dar-se-ão de tal forma que a últimaequação ficaθ 00 = − ⃗ E · ∂ 0⃗ A −12 ( ⃗ E 2 − ⃗ B 2 ) − 1 2 m2 (A 2 0 − ⃗ A 2 ), (4.29)e como sabemos ainda que ⃗ E = −∇A 0 − ∂ 0⃗ A, teremos queθ 00 = − ⃗ E · (− ⃗ E − ∂ 0⃗ A) −12 ( ⃗ E 2 − ⃗ B 2 ) − 1 2 m2 (A 2 0 − ⃗ A 2 ),na qual, efetuando o produto escalar do primeiro termo e agrupando os termos em comum,podemos escreverUsando ainda a propriedade[17]θ 00 = 1 2 ( ⃗ E 2 + ⃗ B 2 ) + ⃗ E · ∇A 0 − 1 2 m2 (A 2 0 − ⃗ A 2 ).∇ · (ϕ ⃗ F ) = ∇ϕ · ⃗F + ϕ∇ · ⃗F , (4.30)na qual ϕ e ⃗ F são, respectivamente, campos escalares e vetoriais quaisquer, podemos reescrevero segundo termo da última equação para θ 00 de tal forma que esta ficará na formaθ 00 = 1 2 ( ⃗ E 2 + ⃗ B 2 ) − A 0 ∇ · ⃗E + ∇ · (A 0⃗ E) −12 m2 (A 2 0 − ⃗ A 2 ).Ao integrarmos a expressão anterior em todo volume e usando o Teorema de Gauss podemosdescartar o terceiro termo da última equação, baseados na idéia de que no infinito os camposse anulam, e assim, após alguma álgebra, obtermosθ 00 = 1 2 ( ⃗ E 2 + ⃗ B 2 + m 2 ⃗ A 2 ) − A 0 ∇ · ⃗E − 1 2 m2 A 2 0,63

que de acordo com (4.8) fica, finalmente, comoθ 00 = 1 [⃗E 2 + B2⃗ 2 + 1 ]m (∇ · ⃗E) 2 + m 2 A ⃗2, (4.31)2que é a expressão para a densidade de energia.A partir do resultado anterior podemos encontrar o operador hamiltoniano integrando adensidade de energia em todo o espaço, ou sejaĤ = 1 ∫2dx 3 [⃗E 2 + ⃗ B 2 + 1 m 2 (∇ · ⃗E) 2 + m 2 ⃗ A2]., (4.32)que, ao proseguirmos com cálculos[9], analogamente com os que foram feitos para encontrar osoperadores hamiltonianos dos campos explorados anteriormente, tais como os campos escalarese eletromagnéticos, podemos mostrar que tal operador fica, em sua forma final, dado por∫Ĥ =dx 3 w k3∑â † kλâkλ, (4.33)que é o operador Hamiltoniano do Campo de Proca, cuja somatória vai de 1 a 3, referêntes àsvariáveis independentes discutidas na secção 4.2 deste capítulo.λ=164

Capítulo 5O Propagador de FeynmanÉ sabido que para se descrever detalhadamente um sistema de muitos corpos, mesmo aindano contexto física clássica, necessitamos conhecer a posição da partícula no decorrer do tempo,ou seja, para cada partícula precisamos conhecer ⃗r(t). Já no caso teoria quântica precisamosconhecer a função de onda dependente do tempo, ou seja, ψ(⃗r, t), que representa a amplitudede probabilidade de encontrar a partícula em uma certa região do espaço. O propagador é oobjeto que promove tanto a evolução temporal quanto espacial de função de onda, ou seja, é opropagador que nos fornece a função de onda em um certo instante e em uma certa região doespaço, quando esta é conhecida numa outra região e instante.Os propagadores de Feynman, no âmbito da Teoria Quântica de Campos, são entendidoscomo sendo amplitudes de probabilidades de se obter processos físicos específicos envolvendointerações nesta teoria[14].5.1 O Propagador do Campo Escalar MassivoO propagador de Feynman, dentro da teotia quântica de campos, é definido como[11]i∆ F (x µ − y µ ) = 〈0| T ( ˆϕ(x µ ) ˆϕ(y µ )) |0〉 , (5.1)sendo que T denota o Produto Ordenamento Temporal, que organiza os campos na formaT ( ˆϕ(x µ ) ˆϕ(y µ )) = θ(x 0 − y 0 ) ˆϕ(x µ ) ˆϕ(y µ ) + θ(y 0 − x 0 ) ˆϕ(y µ ) ˆϕ(x µ ), (5.2)ou seja, que organiza temporalmente a maneira pela qual os campos se propagam.Substituindo (5.2) em (5.1), obtemos quei∆ F (x µ − y µ ) = θ(x 0 − y 0 ) 〈0| ˆϕ(x µ ) ˆϕ(y µ ) |0〉 + θ(y 0 − x 0 ) 〈0| ˆϕ(y µ ) ˆϕ(x µ ) |0〉 , (5.3)65

que de acordo com (2.50) toma a formai∆ F (x µ − y µ ) = θ(x 0 − y 0 )[〈0| ˆϕ (+) (x µ ) ˆϕ (+) (y µ ) |0〉 + 〈0| ˆϕ (+) (x µ ) ˆϕ (−) (y µ ) |0〉 ++ 〈0| ˆϕ (−) (x µ ) ˆϕ (+) (y µ ) |0〉 + 〈0| ˆϕ (−) (x µ ) ˆϕ (−) (y µ ) |0〉]++θ(y 0 − x 0 )[〈0| ˆϕ (+) (y µ ) ˆϕ (+) (x µ ) |0〉 + 〈0| ˆϕ (+) (y µ ) ˆϕ (−) (x µ ) |0〉 ++ 〈0| ˆϕ (−) (y µ ) ˆϕ (+) (x µ ) |0〉 + 〈0| ˆϕ (−) (y µ ) ˆϕ (−) (x µ ) |0〉],na qual podemos notar que em alguns termos temos a aplicação∫ˆϕ (+) (x µ ) |0〉 = dk 3 u k â k |0〉 , (5.4)que de acordo com a equação (2.47), que fornece o valor do operador aniquilação aplicado noestado de vácuo, teremos quecuja correspondente dual é dado porˆϕ (+) (x µ ) |0〉 = 0, (5.5)〈0| ˆϕ (−) (x µ ) = 0. (5.6)A mesma análise é válida para o campo calculado em y µ , desta forma, a definição inicialpara o propagador se resume na formai∆ F (x µ − y µ ) = θ(x 0 − y 0 ) 〈0| ˆϕ (+) (x µ ) ˆϕ (−) (y µ ) |0〉 + θ(y 0 − x 0 ) 〈0| ˆϕ (+) (y µ ) ˆϕ (−) (x µ ) |0〉 . (5.7)Assim, baseados na expressão anterior, podemos entender fisicamente o propagador de Feynmancomo sendo a soma de duas Amplitudes de Probabilidade, de maneira que o primeiro termoé a amplitude de probabilidade de uma partícula ser criada no ponto ⃗y e no instante y 0 paraser aniquilada no ponto ⃗x e no instante x 0 , sendo x 0 maior que y 0 . Já o segundo termo nosfornece a amplitude de probabilidade para a criação de uma partícula no ponto ⃗x e no instantex 0 e desta ser aniquilada no ponto ⃗y e no instante y 0 , sendo y 0 maior que x 0 .Reescrevendo (5.7) já levando em consideração os valores explicitos dos termos do campoem questão dado por (2.62), teremos que∫i∆ F (x µ − y µ dk 3 ∫dk ′3) =2w k (2π) 3 2w k ′(2π) [θ(x 3 0 − y 0 )e −i(kµxµ −k ν ′ yµ) 〈0| â k â † k|0〉 +′+θ(y 0 − x 0 )e i(kµxµ −k ′ ν yµ) 〈0| â k â † k ′ |0〉].66

Considerando a relação de comutação entre os operadores de criação e aniquilação para ocampo escalar já apresentada por nós dada porde onde vem que[â k , â † k ′ ] = δ 3 ( ⃗ k − ⃗ k ′ ),â k â † k ′ = δ 3 ( ⃗ k − ⃗ k ′ ) + â † k ′ â k ,podemos reescrever a última relação para i∆(x µ − y µ ) na forma∫i∆ F (x µ − y µ dk 3 ∫dk ′3) =2w k (2π) 3 2w k ′(2π) [θ(x 3 0 − y 0 )e −i(kµxµ −k νy ′ µ) 〈0| [δ 3 ( ⃗ k − k ⃗′ ) + â † kâ ′ k ] |0〉 ++θ(y 0 − x 0 )e i(kµxµ −k ′ νy µ) 〈0| [δ 3 ( ⃗ k − ⃗ k ′ ) + â † k ′ â k ] |0〉].Como â k |0〉 = 0 e levando em conta (2.18), teremos que∫i∆ F (x µ − y µ dk 3) =2w k (2π) [θ(x 3 0 − y 0 )e −ikµ(xµ −y µ) + θ(y 0 − x 0 )e ikµ(xµ −y µ) ],ou ainda, explicitando os produtos do tipo k µ x µ , temos∫i∆ F (x µ − y µ dk 3) =2w k (2π) [θ(x 3 0 − y 0 )e i⃗ k·(⃗x−⃗y)−iw k (x 0 −y 0 ) + θ(y 0 − x 0 )e −i⃗ k·(⃗x−⃗y)−iw k (x 0 −y 0 ) ].Trocando, no segundo termo, ⃗ k −→ − ⃗ k, esta última assume a forma∫i∆ F (x µ − y µ dk 3) =2w k (2π) 3 ei⃗ k·(⃗x−⃗y) [θ(x 0 − y 0 )e −iw k(x 0 −y 0 ) + θ(y 0 − x 0 )e iw k(x 0 −y 0 ) ]. (5.8)Antes de proseguirmos com o cálculo do propagador propriamente dito nos será de muitarelevância abrir um breve parêntese sobre integrais complexas, que podem ser calculadas pormeio do Teorema do Resíduo[3][4], como por exemplo a integral∮f(z)dz = ±2πi ∑ Resf(z j ), (5.9)c jna qual o resíduo cálculado é obtido por{ }1d(m−1)Resf(z j ) = lim(m − 1)! z↦−→z j dz [f(z)(z − z j) m ] . (5.10)(m−1)Escolhendo o contorno de integração apropriado, podemos mostrar que as quantidades12w ke −iw k(x 0 −y 0 )67

e12w ke iw k(x 0 −y 0 ) ,no propagador que vinhamos calculando, são os resíduos da integral complexa dada por∫e k 0(x 0 −y 0 )dk 0 = −2πi ∑ Resf(wk0 2 − wk2 j ), (5.11)jsendo ±w k os pólos da função localizados no eixo dos reais do plano complexo k 0 . Já as funçõesθ(x 0 − y 0 ) e θ(y 0 − x 0 ) são introduzidas de tal forma que garatam que os resultados encontradosnão divirjam ao tomarmos o limite de ik 0 −→ ∞ (quando fechamos o contorno de integraçãopor cima) e quando tomamos o limite ik 0 −→ −∞ (ao fecharmos o contorno de integração porbaixo).Substituindo (5.11) em (5.8) no nosso propagador teremoslogo,∫ dki∆ F (x µ − y µ 3) = −(2π) 3 ei∫k·(⃗x−⃗y) ⃗ dk0 e −ik 0(x 0 −y 0 ),2πi k0 2 − wk2∫ dk∆ F (x µ − y µ 4e −ikµ(xµ −y µ )) =, (5.12)(2π) 4 k0 2 − wk2e, de acordo com (2.55), a equação (5.12) fica na forma∫ dk∆ F (x µ − y µ 4e −ikµ(xµ −y µ )) =(2π) 4 k µ k µ − m . (5.13)2Como os pólos desta última integral encontram-se no eixo real do plano complexo, umaprática comum nesses casos é deslocar o polo, ou seja, movê-lo de uma distância a −→ 0 desteeixo, assim sendo teremos que∫ dk∆ F (x µ − y µ 4e −ik µ(x µ −y µ )) =(2π) 4 k µ k µ − m 2 + ia . (5.14)Substituindo (5.14) no equação de Klein-Gordon, temos que∫ dk(∂ 2 + m 2 )∆ F (x µ − y µ 4(−k 2 + m 2 )e −ik µ(x µ −y µ )) =(2π) 4 k µ k µ − m 2∫ dk4= −(2π) 4 e−ik µ(x µ −y µ ),que é uma das representações da Delta de Dirac, logo(∂ 2 + m 2 )∆ F (x µ − y µ ) = −δ 4 (x µ − y µ ), (5.15)68

de onde concluímos que o propagador é uma das formas da função de Green para a equação deKlein-Gordon não-homogênea.Note que ao resolvermos a equação (5.15), utilizando o método da Transformada de Fourier[3][4],chegaremos novamente no valor explícito do propagador obtido em (5.14). Para isso, definiremosantes a transformada de Fourier para ∆ F (x µ − y µ ) comoSendo assim, (5.15) ficaI{∆ F (x µ − y µ )} := ∆ F (k µ ). (5.16)I{∂ 2 ∆ F (x µ − y µ )} + m 2 I{∆ F (x µ − y µ )} = −I{δ 4 (x µ − y µ )}, (5.17)e como sabemos que I{∂ 2 ∆ F (x µ − y µ )} = −k 2 ∆ F (k) e ainda I{∆ F (x µ − y µ )} = 1, então como pólo já deslocado teremos que (5.17) será dado por1∆(k) = −k µ k µ − m 2 + ia , (5.18)que é o propagador do campo escalar massivo, definido agora no espaço dos k ′ s.5.2 O Propagador do FótonDe forma similar ao que foi feito na secção anterior obteremos o propagador do fóton ou, sepreferir, do campo eletromagnético. Podemos encontrar este propagador a partir da definição[9]iD µνF (xβ − y β ) = 〈0| T (µ (x β )Âν (y β )) |0〉 , (5.19)sendo que D µνF, por questão de notação, designa o propagador do campo vetorial não massivo.Assim reescrevendo (5.19) substituindo o valor do campo µ , temos∫iD µνF (xβ − y β ) =dk 3 ∫√2wk (2π) 3dk ′3√2wk ′(2π) 33∑λ,λ ′ =0ɛ µ (k, λ)ɛ ν (k ′ , λ ′ )××[θ(x 0 − y 0 )e −i(k βx β −k ′ β yβ) 〈0| â k ′ λ ′↠kλ |0〉 + θ(y 0 − x 0 )e i(kµxµ −k ′ νy µ) 〈0| â kλ â † k ′ λ ′ |0〉].Procedendo da mesma forma que fizemos no caso do campo escalar, considerando as relaçõesde comutação para os operadores de criação e aniquilação para este campo, dadas por (3.27),e a propriedade (2.18), temos que∫iD µνF (xβ − y β ) = −dk 32w k (2π) 3693∑g λλ ɛ µ (k, λ)ɛ ν (k, λ)×λ=0

×[θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ],que segundo a relação (B.12) pode ser escrito na forma∫iD µνF (xβ − y β ) = −g µν dk 32w k (2π) [θ(x 3 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ]. (5.20)Pode-se notar que a integral explicitada em (5.20) já foi identificada (5.13), sendo quedevemos ter o cuidado de perceber que, para este caso, temos m = 0 na relação (2.55) e quepodemos escrever (5.12) lembrando que agora esta encontra-se multiplicada pelo fator −g µν .Assim fazendo podemos escrever queou ainda, já deslocando o pólo, teremosD µνF (xβ − y β ) = −g µν ∫ dk4(2π) 4 e −ik β(x β −y β )k β k β, (5.21)D µνF (xβ − y β ) = −g µν ∫ dk4(2π) 4 e −ik β(x β −y β )k β k β + ia . (5.22)De onde identificamos, com base no que foi feito na seção anterior, queD µνque é o propagador do fóton no espaço dos k ′ s.gµνF (kβ ) = −k β k β + ia , (5.23)Uma análise mais completa deste propagador, ou seja, uma análise que não fixa nenhumvalor para o parâmetro ξ pode ser encontrada na referência[9] deste trabalho, tal análise nosleva ao resultadoF (kβ ) = −gµνk β k β + ia + ξ − 1 k µ k νξ (k β k β + ia) , (5.24)2D µνque por sua vez nos remete a (5.23) ao fixarmos ξ = 1, umja vez que os resultados encontradosnesta secção foram obtidos de acordo com esta escolha para o parâmetro ξ.5.3 O Propagador do Campo de ProcaSimilarmente ao que vinhamos fazendo nas duas primeiras secções deste último capítulo, opropagador do Campo de Proca pode ser calculado de forma explícita a partir da definição[9]i∆ µνF (xβ − y β ) = 〈0| T (µ (x β )Âν (y β )) |0〉 , (5.25)que segue, com a substituição do campo para µ , para∫i∆ µνF (xβ − y β dk 3 ∫dk ′3) = √ √2wk (2π) 3 2wk ′(2π) 3703∑λ,λ ′ =0ɛ µ (k, λ)ɛ ν (k ′ , λ ′ ) (5.26)

[θ(x 0 − y 0 )e −i(k′ β xβ −k β y β) 〈0| â k ′ λ ′↠kλ |0〉 + θ(y 0 − x 0 )e i(k′ β xβ −k ′ β yβ) 〈0| â kλ â † k ′ λ ′ |0〉],que, de acordo com as relações de comutação para os operadores â e â † , mostradas no capítuloanterior, também como nos casos das duas últimas secções, temos∫i∆ µνF (xβ − y β ) =dk 32w k (2π) 33∑ɛ µ (k, λ)ɛ ν (k ′ , λ ′ )[θ(x 0 − y 0 )e −ik β(x β −y β) +λ=0+θ(y 0 − x 0 )e ik β(x β −y β) ],ou ainda, segundo a relação (4.17), está última relação será dada por∫i∆ µνF (xβ − y β ) = −(dk 3g µν − 1 )2w k (2π) 3 m 2 kµ k ν [θ(x 0 − y 0 )e −ik β(x β −y β) + (5.27)+θ(y 0 − x 0 )e ik β(x β −y β) ],na qual percebemos o próprio propagador do campo escalar dado na forma de (5.8), porémexiste uma relevante diferença: o esperado termo de massa.Com o propósito de reescrevermos a integral cujo integrando apresenta o termo − 1 k µ k ν ,m 2partiremos deχ µν = −∂ µ ∂ ν [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ], (5.28)onde as derivadas ∂ µ e ∂ ν atuam na variável x β .Resolvendo (5.28), começaremos baixando os índices das derivadas parciais com o auxíliodo tensor métrico, ou seja,χ µν = −g µα g νρ ∂ ρ ∂ α [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ],que, de acordo com a regra do produto para as derivadas, ficaχ µν = −g µα g νρ ∂ ρ {∂ α [θ(x 0 − y 0 )]e −ik β(x β −y β) + θ(x 0 − y 0 )∂ α e −ik β(x β −y β) + (5.29)+∂ α [θ(x 0 − y 0 )]e ik β(x β −y β) + θ(x 0 − y 0 )∂ α e ik β(x β −y β) }.E ainda, prosseguindo com os cálculos necessários, ficaχ µν = −g µα g νρ ∂ ρ {∂ α [θ(x 0 − y 0 )]e −ik β(x β −y β) + θ(x 0 − y 0 )(−ik β ) ∂xβ∂x α e−ik β(x β −y β) +71

+∂ α [θ(x 0 − y 0 )]e ik β(x β −y β) + θ(x 0 − y 0 )(ik β ) ∂xβ∂x α eik β(x β −y β) },de onde podemos identificar a Deltaδ µ α = ∂xβ∂x α . (5.30)Assim, distribuindo os tensores métricos nesta última soma e já utilizando a propriedade defiltragem de (5.30), temosχ µν = −∂ ρ {g µα g νρ ∂ α [θ(x 0 − y 0 )]e −k β(x β −y β) − ik α g µα g νρ θ(x 0 − y 0 )e −k β(x β −y β) ++g µα g νρ ∂ α [θ(y 0 − x 0 )]e k β(x β −y β) + ik α g µα g νρ θ(y 0 − x 0 )e k β(x β −y β) }.Note que ao aplicarmos o quadri-gradiente ∂ α nas funções θ(x 0 −y 0 ) e θ(y 0 −x 0 ) só teremos contribuiçãopara α = 0, pois as funções aqui mencionadas só apresentam dependencia temporal,logoχ µν = −∂ ρ {g µ0 g νρ ∂ 0 θ(x 0 − y 0 )e −ik β(x β −y β) − ik α g µα g νρ θ(x 0 − y 0 )e −ik β(x β −y β) ++g µ0 g νρ ∂ 0 θ(y 0 − x 0 )e ik β(x β −y β) + ik α g µα g νρ θ(y 0 − x 0 )e ik β(x β −y β) }A derivada da função Teta de Heaviside é a própria Delta de Dirac[3], ou sejaδ(x) = dθ(x)dx .Concordando com está última, temos, também, queAssim sendoδ(x) = − dθ(−x) .dxχ µν = −∂ ρ [g µ0 g νρ δ(x 0 − y 0 )e −ik β(x β −y β) − ik α g µα g νρ θ(x 0 − y 0 )e −ik β(x β −y β) +−g µ0 g νρ δ(x 0 − y 0 )e ik β(x β −y β) + ik α g µα g νρ θ(y 0 − x 0 )e ik β(x β −y β) ].Analogamente, distribuiremos o quadri-gradiente ∂ρ dentro do colchete, assim sendo, teremosχ µν = −g µ0 g ν0 δ ′ (x 0 − y 0 )e −ik β(x β −y β) + ik ρ g µ0 g νρ δ(x 0 − y 0 )e −ik β(x β −y β) +72

+ik α g µα g ν0 δ(x 0 − y 0 )e −ik β(x β −y β) + k α k ρ g µα g νρ θ(x 0 − y 0 )e −ik β(x β −y β) ++g µ0 g ν0 δ ′ (x 0 − y 0 )e ik β(x β −y β) + ik ρ g µ0 g νρ δ(x 0 − y 0 )e ik β(x β −y β) ++ik α g µα g ν0 δ ′ (x 0 − y 0 )e ik β(x β −y β) + k α k ρ g µα g νρ θ(y 0 − x 0 )e ik β(x β −y β) ,ou ainda, levantando os índices usando o tensor métrico, temosχ µν = −g µ0 g ν0 δ ′ (x 0 − y 0 )e −ik β(x β −y β) + ig µ0 k ν δ(x 0 − y 0 )e −ik β(x β −y β) ++ig ν0 k µ δ(x 0 − y 0 )e −ik β(x β −y β) + k µ k ν θ(x 0 − y 0 )e −ik β(x β −y β) ++g µ0 g ν0 δ ′ (x 0 − y 0 )e ik β(x β −y β) + ig µ0 k ν δ(x 0 − y 0 )e ik β(x β −y β) +que, organizado os termos, fica+ig ν0 k µ δ ′ (x 0 − y 0 )e ik β(x β −y β) + k µ k ν θ(y 0 − x 0 )e ik β(x β −y β) ,χ µν = k µ k ν [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ]++i(g µ0 k ν + g ν0 k µ )δ(x 0 − y 0 )[e −ik β(x β −y β) + e ik β(x β −y β) ]+−g µ0 g ν0 δ ′ (x 0 − y 0 )[e −ik β(x β −y β) − e ik β(x β −y β) ].Desta forma podemos reescrever o primeiro termo do lado direito desta última equação, deacordo com (5.28), assim temos[]k µ k ν θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β )== −∂ µ ∂ ν [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ]+ (5.31)[−iδ(x 0 − y 0 )(g µ0 k ν + g ν0 k µ ) e −ik β(x β −y β) + e ik βx β −y β] +[+g µ0 g ν0 δ ′ (x 0 − y 0 ) e −ik β(x β −y β) − e ik βx β −y β] .73

Explicitando (5.27), teremos esta comoi∆ µνF (xβ − y β ) = −g µν ∫dk 32w k (2π) 3 [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ]+∫+dk 32w k (2π) 3 1m 2 kµ k ν [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ].Substituindo (5.31) nesta última relação para o propagador de Proca, temosi∆ µνF (xβ − y β ) = −g µν ∫dk 32w k (2π) 3 [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ]+− 1 m 2 ∂µ ∂ ν ∫dk 32w k (2π) 3 [θ(x 0 − y 0 )e −ik β(x β −y β) + θ(y 0 − x 0 )e ik β(x β −y β) ]+−i 1 m 2 ∫dk 32w k (2π) 3 δ(x 0 − y 0 )(g µ0 k ν + g ν0 k µ )[e −ik β(x β −y β) + e ik β(x β −y β) ]++g µ0 g ν0 1 m 2 ∫dk 32w k (2π) 3 δ′ (x 0 − y 0 )[e −ik β(x β −y β) − e ik β(x β −y β) ].Identificando nos dois primeiros termos desta última equação o propagador escalar dado por(5.8), poderemos reescrever esta, já em função deste propagador, comoi∆ µνF (xβ − y β ) = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆ F (x β − y β )+−i 1 ∫m δ(x 2 0 − y 0 )dk 32w k (2π) 3 (gµ0 k ν + g ν0 k µ )[e −ik β(x β −y β) + e ik β(x β −y β) ]+ (5.32)+g µ0 g ν0 1 ∫m 2 δ′ (x 0 − y 0 )dk 32w k (2π) 3 [e−ik β(x β −y β) − e ik β(x β −y β) ].Podemos reescrever os integrandos dos dois últimos termos da equação (2.41) numa forma quejá nos é familiar mostrada em (5.8), trocando ⃗ k −→ − ⃗ k, implicitos em (5.32), vem daí quei∆ µνF (xβ − y β ) = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆ F (x β − y β )+−i 1 ∫m δ(x 2 0 − y 0 )[e −iw k(x 0 −y 0 ) + e iw k(x 0 −y 0 ) ]dk 32w k (2π) 3 ei⃗ k·(⃗x−⃗y) (g µ0 k ν + g ν0 k µ )+ (5.33)74

+g µ0 g ν0 1 ∫m 2 δ′ (x 0 − y 0 )[e −iw k(x 0 −y 0 ) − e iw k(x 0 −y 0 ) ]dk 32w k (2π) 3 ei⃗ k·(⃗x−⃗y) .Percebemos que no segundo termo desta última equação, a presença de um tensor de segundaordem que representaremos por S µν , ou sejaS µν = (g µ0 k ν + g ν0 k µ ). (5.34)Calculando cada termo de (5.34), podemos junta-los numa matriz que será dada por⎛⎞2w k k 1 k 2 k 3S µν = ⎜ k 1 0 0 0⎟⎝ k 2 0 0 0 ⎠ . (5.35)k 3 0 0 0Com isso, para calcularmos o segundo termo de (5.33), teremos que considerar cada termo de(5.35). Assim sendo, notamos ainda que a única contribuição não nula dar-se-á para o termo S 00desta matriz, uma vez que ao considerarmos as componentes espaciais desta, seremos levadosà calcular algumas integrais do tipo∫ dk3(2π) 3⃗ ke i⃗ k·(⃗x−⃗y) ,que não darão contribuição diferente de zero, já que o integrando é uma função ímpar integradaem todos os valores de ⃗ k. Com isso, concluimos que o termo em questão, já calculado paratodos os termos de (5.35), pode ser reescrito de tal maneira que (5.33) ficará comoi∆ µνF (xβ − y β ) = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆ F (x β − y β )+−ig µ0 g ν0 1 ∫m δ(x 2 0 − y 0 )[e −iw k(x 0 −y 0 ) + e iw k(x 0 −y 0 dk ) 3](2π) 3 ei⃗ k·(⃗x−⃗y) ++g µ0 g ν0 1 ∫m 2 δ′ (x 0 − y 0 )[e −iw k(x 0 −y 0 ) − e iw k(x 0 −y 0 ) ]dk 32w k (2π) 3 ei⃗ k·(⃗x−⃗y) ,que segundo a representação da delta de Dirac dada por∫ dkδ 3 3(⃗x − ⃗y) =(2π) 3 ei⃗ k·(⃗x−⃗y) ,fica na formai∆ µνF (xβ − y β ) = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆ F (x β − y β )+75

−ig µ0 g ν0 1 m 2 δ(x 0 − y 0 )δ 3 (⃗x − ⃗y)[e −iw k(x 0 −y 0 ) + e iw k(x 0 −y 0 ) ]+ (5.36)+g µ0 g ν0 12w k m 2 δ′ (x 0 − y 0 )δ 3 (⃗x − ⃗y)[e −iw k(x 0 −y 0 ) − e iw k(x 0 −y 0 ) ].Antes de prosseguirmos com este cálculo, vejamos quem é a primeira derivada temporal dadelta dada por δ ′ (x 0 − y 0 ). Para isso, comecemos por escrever a integralchamandoI =∫ x2x 1δ ′ (x − a)f(x)dx, (5.37)u = f(x) −→ du = f ′ (x)dxdv = δ ′ (x − a)dx −→ v = δ(x − a).Segundo o método das Integrais por Partes, onde∫ x2udv = uv| x 2x 1−x 1a integral (5.37) será dada por∫ x2∫ x2x 1δ ′ (x − a)f(x)dx = f(x)δ(x − a)| x 2x 1−x 1vdu, (5.38)∫ x2x 1δ(x − a)f ′ (x)dx, (5.39)de acordo com a definição da delta, esta só não é nula para x = a, então o primeiro termodo lado direiro desta última equação será nulo, uma vez que este está sendo calculado em doispontos que não coencidem com a sigularidade, logo a (5.39) fica na forma∫ x2x 1δ ′ (x − a)f(x)dx = −que assim faz sentido a relação dada por[9]∫ x2x 1δ(x − a)f ′ (x)dx,δ ′ (x − a)f(x) −→ −δ(x − a)f ′ (x). (5.40)Então, o último termo de (5.36) poderá ser reescrito de tal forma que esta equação serádada pori∆ µνF (xβ − y β ) = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆ F (x β − y β )+−ig µ0 g ν0 1 m 2 δ(x 0 − y 0 )δ 3 (⃗x − ⃗y)[e −iw k(x 0 −y 0 ) + e iw k(x 0 −y 0 ) ]+ (5.41)+ig µ0 g ν0 12m 2 δ(x 0 − y 0 )δ 3 (⃗x − ⃗y)[e −iw k(x 0 −y 0 ) + e iw k(x 0 −y 0 ) ].76

E ainda, compactificando as deltas explicitas na última equação, poderemos reescrevê-la comoi∆ µνF (xβ − y β ) = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆ F (x β − y β )+−ig µ0 g ν0 1 m 2 δ4 (x β − y β )[e −iw k(x 0 −y 0 ) + e iw k(x 0 −y 0 ) ]+ (5.42)+ig µ0 g ν0 12m 2 δ4 (x β − y β )[e −iw k(x 0 −y 0 ) + e iw k(x 0 −y 0 ) ].Então, o propagador do campo de proca toma a formai∆ µνF (xβ − y β ) = −i(g µν + 1 )m 2 ∂µ ∂ ν ∆ F (x β − y β ) −im 2 gµ0 g ν0 δ 4 (x β − y β ). (5.43)Uma observação importante a ser feita é que o segundo termo do propagador acima,aparentemente, quebra a covariância de Lorentz, uma vez que neste está sendo consideradoque x 0 = y 0 . Porém este termo não é relevante uma vez que o mesmo é cancelado no desenvolvimentoda Teorida de Perturbação[9][11]. Uma outra maneira de lidarmos com eleé simplesmente omitindo-o[11], uma vez que do ponto de vista físico este não dará nenhumacontribuição.Temos também, finalmente, que de acordo com a forma explícita de ∆ F dado por (5.14),podemos tomar sua derivadas, como indicado em (5.43), e escrevê-lo como∆ µνF (k) = − ( g µν − 1 m 2 k µ k ν)k β k β − m 2 + ia − 1 m 2 gµ0 g ν0 . (5.44)ou seja, o propagador de Feynman para o Campo de Proca no espaço dos k ′ s.77

ConclusãoExploramos neste trabalho o método da quantização canônica de alguns campos importantesque surgem no contexto da Teoria Quântica de Campos. Vimos, primeiramente, que a idéia decampo surge de uma distribuição de quantidades discretas quando estas tendem ao contínuonuma determinada região. Assim fazendo, fomos capazes de mostrar que este limite ao contínuode um conjunto de osciladores acoplados tem a dinâmica regida pela própria equação da onda,cuja solução foi quantizada. Percebemos na quantização dos campos escalares, quando submetidosa condições de contorno periódicas, que estes apresentam um comportamento similarcom os encontrados como solução no processo de quantização da corda.Ao quantizarmos o campo eletromagnético livre percebemos a necessidade de impormossobre este uma escolha de calibre, seja o Calibre de Coulomb ou o Calibre de Lorentz. Sendoque, neste último, fez-se necessária a consideração de uma densidade de Lagrangeana modificadapara mantermos a consistência com a proposta de quantização covariante. Com issoconstatamos que a escolha do calibre de Lorentz, contrariamente ao que ocorre com o calibrede Coulomb, implica em dois novos graus de liberdade para a polarização do campo em questão,sendo estes eliminados por argumentos físicos mediantes as inconsistências que eles trazem paraa teoria, esta eliminação é feita lançando-se mão do Método de Gupta-Bleuler. Assumindoa condição imposta por esse método fomos capazes de mostrar que o campo de Proca satisfaz aescolha de calibre de Lorentz, concluindo assim que quando falamos no campo eletromagnético,estamos falando, também, num campo que apresenta apenas 2 graus de polarização, ambostransversais.Mostramos que, motivados por um processo de quantização aparentemente não covariantepara o campo de Proca, tanto os campos escalares quanto os campos vetoriais adimitem umprocesso de quantização dito covariante, sendo para isso necessária a definição de uma funçãoinvariante chamada de Função de Pauli-Jordan. Com esta mostramos que as quantizaçõesque vínhamos efetuando anteriormente (para tempos iguais) são apenas um caso particular deum processo de quantização mais geral, escrito em termos deste invariante.78

Por fim, obtivemos o propagador de Feynman para vários campos importantes, concebendoque, no contexto da Teoria Quântica de Campos, o propagador deve ser entendido como sendo aAmplitude de Probabilidade de ocorrência de processos de criação e aniquilação de partículas apartir do vácuo quântico ordenados temporalmente, e representando a propagação da interaçãoentre campos em pontos diferentes no espaço-tempo.79

Apêndice AO Eletromagnetismo de MaxwellNeste apêndice faremos uma pequena apresentação da Teoria Eletromagnética, nos detendo,com maior atenção, às próprias Equações de Maxwell e suas representações através dospontenciais escalares e vetoriais e as liberdades de escolha de calibre concernentes a estes potenciais.Feito isso vamos apresentar as equações fundamentais do eletromagnetismo em suaforma covariante, definida em termos do Tensor de Maxweel-Faraday.As Equações de MaxwellA teoria eletromagnética é descrita, basicamente, pos dois vetores: o vetor campo elétrico⃗E e o vetor indução magnética ⃗ B; sendo estes soluções das equações de Maxwell, dadas por∇ · ⃗E = ρ,(A.1)∇ · ⃗B = 0,(A.2)∇ × ⃗ E = − ∂ ⃗ B∂t ,(A.3)∇ × ⃗ B = ⃗j + ∂ ⃗ E∂t ,(A.4)sendo estas, respectivamente, a Lei de Gauss, a Lei do Monopólo Magnético, a Lei deFaraday e a Lei de Ampère[17]. Tais equação estão escritas segundo o sistema de unidades deLorentz-Heaviside, onde omitimos os termos 4π presentes nas equações de Maxwell quandoescritas segundo o sistema de unidades Gaussianas[17], e ainda, fizemos nestas últimas c = 1,de acordo com (1.69).80

As densidades de carga ρ(⃗x, t) e de corrente ⃗j(⃗x, t) são as fontes do campo, relecionadasentre si por⃗j = ρ⃗v,(A.5)sendo que o fato destas distribuições não aprecerem nas equações (A.2) e (A.3) dão a essasa denominação de equações homogêneas de Maxwell, enquanto as outras são ditas não homogêneas.As equações de Maxwell admitem ainda uma equação da continuidade dada por∂ρ∂t + ∇ · ⃗j = 0,(A.6)sendo que esta equação remete a um importante princípio físico: o princípio da conservação dacarga.Temos ainda que os campos E ⃗ e B ⃗ derivam de potenciais escalares ϕ(⃗x, t) e vetoriais A(⃗x, ⃗ t),conforme as relações⃗E = −∇ϕ − ∂ ⃗ A∂t(A.7)e⃗B = ∇ × ⃗ A,(A.8)substituindo estas duas últimas na equação (A.4), teremos que(∇ × (∇ × A) ⃗ = ⃗j + ∂ −∇ϕ − ∂ ⃗ )A.∂t ∂tComo para um campo vetorial qualquer ⃗ F , temos a propriedade[17]∇ × ∇ × ⃗ F = ∇(∇ · ⃗F ) − ∇ 2 ⃗ F .(A.9)temos∇(∇ · ⃗A) − ∇ 2 ⃗ A= ⃗j − ∇ ∂ϕ∂t − ∂2 ⃗ A∂t 2 ,que, ao agruparmos as funções cujo operador gradiente está nestas aplicado, temos∂ 2 A ⃗(∂t − 2 ∇2 A ⃗ = ⃗j + ∇ ∇ · ⃗A + ∂ϕ ).∂t81

Neste ponto é de grande relevância frizarmos que existem uma infinidade de pares (ϕ, ⃗ A)que geram ( ⃗ E, ⃗ B). Por conveniência podemos escolher esses potenciais de tal forma que∇ · ⃗A + ∂ϕ∂t = 0.(A.10)Tal relaçãos se dá por uma escolha de calibre denominada Calibre de Lorentz, que nos remetea∂ 2 ⃗ A∂t 2 − ∇2 ⃗ A = ⃗j, (A.11)da qual notamos que o potencial vetorial é solução da equação da onda não homogenea.Uma outra escolha de calibre que também pode ser feita tomando ∇ · ⃗A = 0 é conhecidacomo Calibre de Coulomb que por sua vez pode ser útil em diversas circunstâncias.Como existem uma infinidade de pares de (ϕ, ⃗ A) que geram ( ⃗ E, ⃗ B), podemos tomar outrospares (ϕ ′ , ⃗ A ′ ) relacionados a (ϕ, ⃗ A) da seguinte formaϕ ′ −→ ϕ − ∂Λ∂t(A.12)e⃗A ′ −→ ⃗ A + ∇Λ,(A.13)nas quais Λ = Λ(⃗x, t) é uma função escalar qualquer que também satisfaz o calibre de Lorentz[16].Esta mudança para novos potenciais é denominada Transformação de Padrão ou Liberdadede Calibre do Eletromagnetismo[16].As Equações de Maxwell na sua Forma CovarianteNão é nosso principal objetivo mostrar que de fato as equações de Maxweel admitem umarepresentação covariante, tal feito pode ser encontrado de forma mais detalhada na referência[12] deste trabalho. Contudo, tomando isso como verdade temos que as distribuições de cargaρ e de corrente ⃗j relacionadas entre si comoj µ = (ρ,⃗j),(A.14)denominada quadri-corrente eletromagnética, que, por sua vez, gera um campo da formaA µ = (ϕ, ⃗ A).(A.15)82

chamado quadri-potencial eletromagnético.Note ainda que as liberdades de calibre dadas pelas equações (A.11) e (A.12) podem serescritas nesta forma comoA ′ µ −→ A µ − ∂ µ Λ,(A.16)e que de acordo com as equações (A.7) e (A.8), se nota que os campos E ⃗ e B ⃗ são obtidos apartir das derivadas dos potenciais, logo esperamos que os campos estejam escritos em formacovariante de alguma maneira que envolvam as derivadas destes quadri-potenciais, com issodefinimos o chamado Tensor de Maxwell-Faraday, dado porF µν := ∂ µ A ν − ∂ ν A µ ,(A.17)que é antissimétrico. Logo vem daí queF µν = −F νµ .(A.18)Encontraremos agora a forma explícita do tensor de Maxwell sendo que, para isso, é importanteencontrarmos os componentes covariantes da equação (A.15) que, segundo o tensormétrico, pode ser reescrita comoA µ = g µν A ν = (ϕ, − ⃗ A),sendo g µν denominado de Tensor Métrico de Mikowski e dado explicitamente por⎛⎞1 0 0 0g µν = g µν = ⎜ 0 −1 0 0⎟⎝ 0 0 −1 0 ⎠ ,0 0 0 −1(A.19)(A.20)que tem como uma de suas funções, a propriedade de “levantar” e “baixar” índices de grandezastensoriais como foi feito, por exemplo, em (A.19).Para µ = 0, calcularemos a equação (A.17) fazendo ν = 0, 1, 2, 3 tendo em vista a equação(A.18). Logo teremos:Para ν = 0:F 00 = ∂ 0 A 0 − ∂ 0 A 0 ,que ficaF 00 = 0.(A.21)83

Para ν = 1:F 01 = ∂ 0 A 1 − ∂ 1 A 0 ,como 1 designa a componente x, bem como 0 a componente temporal, temosF 01 = − ∂A x∂t− ∂ϕ∂x ,que são as componentes x do gradiente de ϕ e a derivada temporal da componente x do campo⃗A, assim(F 01 = −∇ϕ − ∂ A ⃗ ),∂tque segundo (A.7), ficaxF 01 = E x .(A.22)Analogamente teremos para ν = 2:que ficaF 02 = ∂ 0 A 2 − ∂ 2 A 0 ,F 02 = E y .(A.23)E finalmente para ν = 3:F 03 = ∂ 0 A 3 − ∂ 3 A 0 ,de onde vemF 03 = E z .(A.24)E usando (A.18) encontraremos ainda queF 10 = −E xF 20 = −E yF 30 = −E z .(A.25)Note a partir da própria definição do tensor de Maxwell que os componentes deste para µ = νsão nulas, portanto proseguiremos com os cálculos unicamente para µ ≠ ν.Assumindo agora µ = 1 e variando ν, teremos, de forma análoga ao que fizemos até então,as seguintes relações:84

Para ν = 2:F 12 = ∂ 1 A 2 − ∂ 2 A 1 ,F 12 = −B z .(A.26)Para ν = 3:F 13 = ∂ 1 A 3 − ∂ 1 A 3 ,F 13 = B y .(A.27)De onde concluimos, devido a propriedade de antissimetria do tensor de Maxwell, queF 21 = B zF 31 = −B y .(A.28)E finalmente as contribuições não nulas que ainda nos resta calcular virão ao assumirmosµ = 2 e ν = 3, logoF 23 = ∂ 2 A 3 − ∂ 3 A 2 ,F 23 = −B x .(A.29)Portanto,F 32 = B x .(A.30)Então, de acordo com as relações que vão de (A.21) até (A.30), podemos escrever o tensorde Maxwell em sua forma matricial comoF µν =⎛⎜⎝0 E x E y E z−E x 0 −B z B y−E y B z 0 −B x−E z −B y B x 0⎞⎟⎠ ,(A.31)sendo que as componentes contravariantes deste são dadas porF µν = g µρ g νβ F ρβ ,(A.32)85

logoF µν =⎛⎜⎝0 −E x −E y −E zE x 0 −B z B yE y −B z 0 −B xE z B y B x 0⎞⎟⎠ ,(A.33)na qual podemos notar que este é um tensor antissimétrico (como já visto antes) cujos elementossão as componentes dos campos vetoriais E ⃗ e B. ⃗Pela própria construção do Tensor de Maxwell-Faraday percebemos que esse tensor satisfazas relações diferenciais dadas na forma∂ [σ F µν] = 0,(A.34)na qual as equações homogêneas de Maxweel estão contidas nesta última relação. Para mostrarmosisso façamos primeiramente (σ, µ, ν) = (0, 1, 2), daí escrevemos que∂ 0 F 12 + ∂ 2 F 01 + ∂ 1 F 20 = 0,e como já identificamos todas as componentes do tensor F µν , esta última será reescrita comoou ainda− ∂B z∂t+ ∂E x∂y − ∂E y∂x = 0,∂E y∂x − ∂E x∂y = −∂B z∂t .(A.35)Uma vez que o rotacional, em coordenadas cartezianas, de uma função vetorial qualquer ⃗ F , édado por[17]∇ × ⃗ F =e seu divergente por( ∂Fz∂y − ∂F ) (y ∂Fxˆx +∂z ∂z − ∂F ) (z ∂Fyŷ +∂x ∂x − ∂F )xẑ, (A.36)∂y∇ · ⃗F = ∂F x∂x + ∂F y∂y + ∂F z∂z ,(A.37)podemos identificar na relação (A.35) a componente z do rotacional do campo E, ⃗ assim sendo((∇ × E) ⃗ ∂Bz = −⃗ ). (A.38)∂tAgora, para (σ, µ, ν) = (0, 1, 3), teremos que∂ 0 F 13 + ∂ 3 F 01 + ∂ 1 F 30 = 0,86z

que de maneira análoga ao caso anterior, ficará como((∇ × E) ⃗ ∂By = −⃗ )∂ty. (A.39)Do mesmo modo para (σ, µ, ν) = (0, 2, 3) teremos((∇ × E) ⃗ ∂Bx = −⃗ ), (A.40)∂txe ainda, para (σ, µ, ν) = (1, 2, 3) vem quede onde seguePortanto, segundo a relação (A.37), temos∂ 1 F 23 + ∂ 3 F 12 + ∂ 2 F 31 = 0,− ∂B x∂x − ∂B y∂y − ∂B z∂z = 0.∇ · ⃗B = 0.(A.41)Da qual concluímos que as relações contidas em (A.34) carregam consigo as equações (A.2) e(A.3).Já as equações não homogêneas estão contidas em∂ µ F µν = j ν .(A.42)Para mostrarmos isso, calcularemos esta relação para ν = 0, 1, 2, 3 fixos e variando µ.Para ν = 0:∂ 0 F 00 + ∂ 1 F 10 + ∂ 2 F 20 + ∂ 3 F 30 = j 0 .De onde, de acordo com o tensor F µν e com (A.37), teremos que∇ · ⃗E = ρ.(A.43)Prosseguindo com os cálculos para os outros valores de ν = 1, 2, 3, encontraremos para ν = 1 aseguinte relação((∇ × B) ⃗ x = ⃗j + ∂ E ⃗ )∂t87x. (A.44)

Resultado similar aos que podemos encontrar para ν = 2, 3, de maneira que somos levados àconcluir que as equações (A.1) e (A.4) estão contempladas em (A.42).Ao considerarmos a ausência de fontes, ou seja, quej µ = 0,(A.45)teremos∂ µ F µν = 0,(A.46)o que, por sua vez, nos remetará, de maneira análoga ao que vinhamos fazendo até então, aoresultado∇ · ⃗E = 0(A.47)e∇ × ⃗ B = ∂ ⃗ E∂t .(A.48)Embasados no que foi explorado até então podemos concluir que a Teoria Eletromagnéticade Maxwell adimite uma representação tensorial covariante, logo a mesma se trata de umateoria invariante perante uma transformação de Lorentz. Isso significa que dado um observadorno referencial S, que caracteriza completamente o campo eletromagnético por F µν e j ν , e umoutro observador S’, que se move em relação a S, e que caracteriza completamente o mesmocampo por F ′ µν e j ′ ν , temos que ambos utilizarão da mesma lei do eletromagnetismo paradescrever este campo.Assim, para S teremose para S’ teremos∂ µ F µν = j ν∂ [σ F µν] = 0,∂ µ F ′µν = j ′ν∂ [σ F ′ µν] = 0.(A.49)(A.50)Temos ainda que as escolhas de calibre mensionadas anteriormente podem serem escritasneste formalismo como∂ i A i = 0,(A.51)denominado Calibre de Coulomb, e ainda∂ µ A µ = 0,(A.52)denominado Calibre de Lorentz.88

Apêndice BOs Vetores de PolarizaçãoDesde o Capítulo 3 nos deparamos com os chamados vetores de polarização, importantespara a descrição dos campos vetorias. Explicitaremos agora algumas sutilezas que são derelevância para o seu melhor entendimento, bem como para uma melhor noção de como estesvetores são definidos para os casos massivos e não massivos.Para a construção dos vetores de polarização ɛ µ (k, λ) comecemos por mostrar a relação deortonormalidade[9] que tais vetores devem satisfazer, e que é dada porɛ µ (k, λ)ɛ µ (k, λ ′ ) = g λλ ′.(B.1)Para o caso do campo vetorial massivo escolheremos uma estrutura para os vetores depolarização de tal forma que os seus dois estados de polarização transversais podem ser dadosporɛ µ (k, 1) = (0,⃗ɛ(k, 1))ɛ µ (k, 2) = (0,⃗ɛ(k, 2)),(B.2)nos quais os produtos escalares entre tais vetores e k µ , são dados pork µ ɛ µ (k, 1) = k µ ɛ µ (k, 2) = 0(B.3)e ainda⃗ɛ(k, i) · ⃗ɛ(k, j) = δ ij .(B.4)O estado de polarização ɛ µ (k, 3) é construido de maneira que coincida com o vetor de onda⃗ k, logok µ ɛ µ (k, 3) = 0. (B.5)89

que, multiplicando ambos os lados da igualdade por ɛ ν (k, λ), teremosg µν ɛ µ (k, λ)ɛ ν (k, λ ′ )ɛ ν (k, λ) = g λλ ′ɛ ν (k, λ),que, concordando com a própria relação (B.1), ficag µν g λλ ′ɛ µ (k, λ) = g λλ ′ɛ ν (k, λ),e multiplicando agora por ɛ µ (k, λ ′ )g µν g λλ ′ɛ µ (k, λ)ɛ µ (k, λ ′ ) = g λλ ′ɛ ν (k, λ)ɛ µ (k, λ ′ ),que ficará comog µν g λλ ′g λλ′ = g λλ ′ɛ ν (k, λ)ɛ µ (k, λ ′ ),como, segundo a relação (A.20), g λλ ′ = g λλ′ , e de sabendo ainda que g λλ ′g λλ′ = δ λλ ′, utilizaremosa propriedade de filtragem desta, e assim teremosg µν = g λλ ɛ ν (k, λ)ɛ µ (k, λ),(B.12)que pode ainda ser escrita comog µν = g 00 ɛ ν (k, 0)ɛ µ (k, 0) +3∑g λλ ɛ ν (k, λ)ɛ µ (k, λ).Como g 00 = 1 e g λλ = -1 para λ = 1, 2, 3, e utilizando ainda a equação (B.10), temosou ainda3∑λ=1g µν =1 m 2 kµ k ν −λ=13∑ɛ µ (k, λ)ɛ ν (k, λ),λ=1ɛ µ (k, λ)ɛ µ (k, λ) = −(g µν − 1 )m 2 kµ k ν . (B.13)Já para a construção dos estados de polarização para o campo vetorial não massivo, começariamosdefinindo os estados de polarização transversais que seriam dados, também, pela relação(B.2). Veja nas equações (B.7) e (B.10) que a obtenção dos estados de polarização longitudinale escalar não são tão imediatos quanto os estados de polarização transversal. Como para o casonão massivo o que nos trás resultados físicos são apenas os fótons transversais, não exploraremoseste caso para os outros estados de polarização uma vez que os mesmos são automaticamenteeliminados por argumentos físicos. Uma discussão mais detalhada sobre estes argumentos podeser encontrada na referência[9] desta monografia.91

Apêndice CPropriedades Matemáticas da Funçãode Pauli-JordanNeste apêndice mostraremos que a função de Pauli-Jordan, introduzida na secção 4.2 destetrabalho, satisfaz algumas propriedades de suma importância para que percebamos que asrelações de comutação entre os operadores de campo, calculadas em pontos arbitrários doespaço-tempo, se remetem às relações de comutações calculadas para tempos iguais, sendoestas um caso particular de relações mais gerais.A função de Pauli-Jordan pode, também, ser escrita como[9]∫ dk∆(x µ − y µ 3sin[k µ (x µ − y µ )]) = −, (C.1)(2π) 3 w ksendo que na própria estrutura da equação (C.1) pode-se perceber que esta é uma função ímpar,ou seja, que∆(x µ − y µ ) = −∆(y µ − x µ ).(C.2)Reescrevendo a equação (C.1) na forma∫ dk∆(x µ − y µ 3sin[w k (x 0 − y 0 ) −) = −⃗ k · (⃗x − ⃗y)], (C.3)(2π) 3 w kque, calculada em tempos iguais, é dada por∫ dk∆(x µ − y µ 3sin[−)| x0 =y 0= −⃗ k · (⃗x − ⃗y)].(2π) 3 w kComo a função senoidal é ímpar, temos ainda∫ dk∆(x µ − y µ 3sin[)| x0 =y 0=⃗ k · (⃗x − ⃗y)],(2π) 3 w k92

que, de acordo com[20]sin θ = eiθ − e −iθ,2ificamos com∆(x µ − y µ )| x0 =y 0=∫ dk3e i⃗ k·(⃗x−⃗y)∫ dk3e −i⃗ k·(⃗x−⃗y)−.(2π) 3 2iw k (2π) 3 2iw kTrocando no segundo termos desta última relação ⃗ k −→ − ⃗ k, temos, finalmente, que a funçãode Paulin-Jordan é nula quando calculada em tempos iguais, ou seja, que∆(x µ − y µ )| x0 =y 0= 0.(C.4)Calculando agora a primeira derivada temporal (em relação à x 0 ) de (C.3), temos∫ dk∂ 0 ∆(x µ − y µ 3) = −(2π) cos[w k(x 3 0 − y 0 ) − ⃗ k · (⃗x − ⃗y)],que para tempos iguais e levando em consideração que a função cosseno é ímpar, é dada por∫ dk∂ 0 ∆(x µ − y µ 3)| x0 =y 0= −(2π) cos[⃗ k · (⃗x − ⃗y)],3que, de acordo com[20]pode ser escrita comocos θ = eiθ + e −iθ,2∫ dk∂ 0 ∆(x µ − y µ 3e i⃗ k·(⃗x−⃗y)∫ dk3e −i⃗ k·(⃗x−⃗y))| x0 =y 0= −−,(2π) 3 2 (2π) 3 2na qual, trocando, novamente no segundo termo, ⃗ k −→ − ⃗ k, temos∫ dk∂ 0 ∆(x µ − y µ 3)| x0 =y 0= −(2π) 3 ei⃗ k·(⃗x−⃗y) ,que é uma das representações da Delta de Dirac, logo∂ 0 ∆(x µ − y µ )| x0 =y 0= −δ 3 (⃗x − ⃗y).(C.5)E, por fim, um outro resultado importante a ser obtido dar-se-à ao aplicarmos na função dePauli-Jordan o operador ∂ µ ∂ µ + m 2 . Fazendo isso e já usando o tensor métrico, ficamos com(∂ µ ∂ µ + m 2 )∆(x µ − y µ ) = (g µν ∂ µ ∂ ν + m 2 )∆(x µ − y µ ). (C.6)93

Calculando o primeiro termo desta última equação, utilizando para isso a representação (C.1),temos∂ µ ∂ µ ∆(x µ − y µ ) = −g µν ∂ µ ∂ ν∫ dk3(2π) 3 sin[k µ (x µ − y µ )]w k,aplicando ainda o quadri-gradiente ∂ ν no integrando da relação acima, temosque pode ser escrita como∂ µ ∂ µ ∆(x µ − y µ ) = −g µν ∂ µ∫ dk3(2π) 3 k µw kδ ν µ cos[k µ (x µ − y µ )],∂ µ ∂ µ ∆(x µ − y µ ) = −g µν ∂ µ∫ dk3(2π) 3 k νw kcos[k µ (x µ − y µ )].De maneira análoga ao caso anterior, aplicaremos o operador ∂ µ , assim∂ µ ∂ µ ∆(x µ − y µ ) = g µν ∫ dk3(2π) 3 k ν k µw ksin[k µ (x µ − y µ )],que, segundo o tensor métrico, fica∫ dk∂ µ ∂ µ ∆(x µ − y µ 3k µ k µ) =sin[k(2π) 3 µ (x µ − y µ )]. (C.7)w kSubstituindo (C.7) em (C.6), temos∫ dk(∂ µ ∂ µ + m 2 )∆(x µ − y µ 3k µ k µ∫ dk) =sin[k(2π) 3 µ (x µ − y µ 3m 2)] −sin[kw k(2π) 3 µ (x µ − y µ )]w kou ainda∫ dk(∂ µ ∂ µ + m 2 )∆(x µ − y µ 3(k µ k µ − m 2 )) =sin[k(2π) 3 µ (x µ − y µ )].w kComo k µ k µ = w 2 k − ⃗ k 2 e sabendo ainda que w 2 k = ⃗ k 2 + m 2 , temos, finalmente, que(∂ µ ∂ µ + m 2 )∆(x µ − y µ ) = 0, (C.8)ou seja, a função de Pauli-Jordan é solução da equação homogênea de Klein-Gordon.94

Bibliografia[1] ALVES, V.S.S., Notas de aula do curso de Métodos Matemáticos para a Física Teórica,UFPA, 2006.[2] BASSALO, J.M.F., Eletrodinâmica Quântica, Editora Livraria da Física, 2006.[3] BASSALO, J.M.F., Métodos da Física Teórica II, Editora Universitária UFPA, 1989.[4] BUTKOV, E., Física Matemática, Editora LTC, 1988.[5] CARAMES, T.R.P. Conseqüências Quânticas e Relativísticas da Compacidade do Espaço,Trabalho de Conclusão de Curso, UFPA, 2007.[6] DAS, A.,Proceedings of the seventh MRST meeting, ed. A. Das 1985.[7] EISBERG, R.; RESNICK, R.,Física Quântica, Editora Campus. Das 1974.[8] GOMES, M.O.C.,Teoria Quântica dos Campos, EDUSP, 2002.[9] GREINER, W.; Reinhardt, J., Field Quantization, Editora Springer, 1986.[10] GROSS, F., Relativistic Quantum Mechanics and Field Theory, Editora Wiley Interscience,1993.[11] ITZYKSON, C.; ZUBER, J.B.Quantun Field Theory, McGraw-Hill International Editions,1985.[12] LIMA, M., Introdução à Relatividade Especial, Ainda não Publicada, UFPA.[13] MANDL, F.; SHAW, G., Quantum Field Theory, Addison John Wiley, 1993.[14] MATTUCK, R.D.,A Guide to Feynman Diagrams in the Many-Body Problem, DoverPublication, 1976.95

[15] PASSOS, E.M.R., Aspectos Básicos Sobre a Quantização Canônica do Campo Eletromagnético,Trabalho de Conclusão de Curso, UFPA, 1999.[16] PIZA, A.F.R. de Toledo, Mecânica Quântica, EDUSP, 2003.[17] REITZ, J.R.; MILFORD, F.J.; CHRISTY, R.W., Fundamentos da Teoria Eletromagnética,Editora Campus, 1982.[18] RYDER, L.H., Quantum Field Theory - Second Edition, Editora Cambridge, 1996.[19] SAKURAI, J.J., Modern Quantum Mechanics, Addison-Wesley Publishing Company,1994.[20] SYMON, K.R., Mecânica, Editora Campus, 1971.[21] VIZEU. S., Notas de aula do curso de Mecânica Quântica, UFPA, 2006.96