Funktsiooni piirväärtus ja pidevus
Funktsiooni piirväärtus ja pidevus
Funktsiooni piirväärtus ja pidevus
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
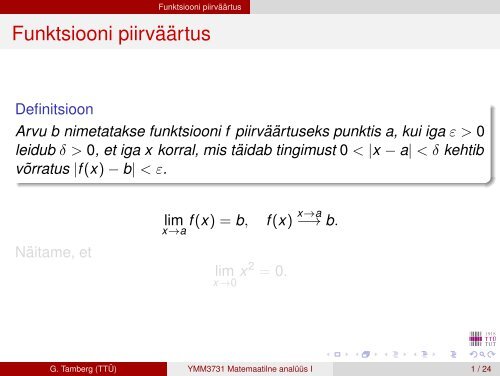
Definitsioon<br />
Arvu b nimetatakse funktsiooni f <strong>piirväärtus</strong>eks punktis a, kui iga
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Definitsioon<br />
Arvu b nimetatakse funktsiooni f <strong>piirväärtus</strong>eks punktis a, kui iga
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
<strong>Funktsiooni</strong>l f eksisteerib <strong>piirväärtus</strong> punktis a para<strong>ja</strong>sti siis kui iga<br />
<strong>ja</strong>da {xn}, mis koondub punktiks a (xn ∕= a) korral <strong>ja</strong>da {f (xn)} koondub<br />
arvuks b.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 2 / 24
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Suurust +∞ nimetatakse funktsiooni f <strong>piirväärtus</strong>eks punktis a, kui iga<br />
M > 0 leidub
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Suurust +∞ nimetatakse funktsiooni f <strong>piirväärtus</strong>eks punktis a, kui iga<br />
M > 0 leidub
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Ühepoolsed <strong>piirväärtus</strong>ed<br />
Definitsioon<br />
Arvu b nimetatakse funktsiooni f vasakpoolseks <strong>piirväärtus</strong>eks punktis<br />
a, kui iga
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Suurust +∞ nimetatakse funktsiooni f vasakpoolseks <strong>piirväärtus</strong>eks<br />
punktis a, kui iga M > 0 leidub
Piirväärtuse omadusi<br />
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Konstantse funktsiooni <strong>piirväärtus</strong>eks on see konstant, st.<br />
Lause<br />
∀x ∈ X(f (x) = c) =⇒ lim<br />
x→a f (x) = c.<br />
Kui funktsioonil f (x) leidub <strong>piirväärtus</strong> punktis a, siis leidub punkti a<br />
selline
Piirväärtuse omadusi<br />
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Konstantse funktsiooni <strong>piirväärtus</strong>eks on see konstant, st.<br />
Lause<br />
∀x ∈ X(f (x) = c) =⇒ lim<br />
x→a f (x) = c.<br />
Kui funktsioonil f (x) leidub <strong>piirväärtus</strong> punktis a, siis leidub punkti a<br />
selline
Piirväärtuse omadusi<br />
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Konstantse funktsiooni <strong>piirväärtus</strong>eks on see konstant, st.<br />
Lause<br />
∀x ∈ X(f (x) = c) =⇒ lim<br />
x→a f (x) = c.<br />
Kui funktsioonil f (x) leidub <strong>piirväärtus</strong> punktis a, siis leidub punkti a<br />
selline
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Piirväärtuse omadusi (2)<br />
Lause<br />
Kui funktsioonidel f (x) <strong>ja</strong> g(x) on punktis a sama <strong>piirväärtus</strong> b ning<br />
leidub punkti a
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Piirväärtuse omadusi (2)<br />
Lause<br />
Kui funktsioonidel f (x) <strong>ja</strong> g(x) on punktis a sama <strong>piirväärtus</strong> b ning<br />
leidub punkti a
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Piirväärtuse omadusi (2)<br />
Lause<br />
Kui funktsioonidel f (x) <strong>ja</strong> g(x) on punktis a sama <strong>piirväärtus</strong> b ning<br />
leidub punkti a
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Piirväärtuse omadusi (2)<br />
Lause<br />
Kui f (x) x→a<br />
−→ A, g(x) x→a<br />
−→ B <strong>ja</strong> c ∈ ℝ, siis<br />
Lause<br />
lim (c ⋅ f (x)) = c ⋅ lim f (x) = c ⋅ A,<br />
x→a x→a<br />
lim (f (x) + g(x)) = lim f (x) + lim g(x) = A + B,<br />
x→a x→a x→a<br />
( ) (<br />
lim (f (x) ⋅ g(x)) = lim f (x) ⋅ lim<br />
x→a x→a x→a g(x)<br />
)<br />
= A ⋅ B<br />
f (x)<br />
f (x) B∕=0<br />
lim =<br />
x→a g(x)<br />
lim<br />
x→a<br />
lim<br />
x→a<br />
g(x) = A<br />
B .<br />
(<br />
lim 1 +<br />
x→+∞<br />
1<br />
) x<br />
(<br />
= e, lim 1 +<br />
x<br />
x→−∞<br />
1<br />
) x<br />
= e, lim (1 + x)<br />
x<br />
x→0 1/x = e.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 8 / 24
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Piirväärtuse omadusi (2)<br />
Lause<br />
Kui f (x) x→a<br />
−→ A, g(x) x→a<br />
−→ B <strong>ja</strong> c ∈ ℝ, siis<br />
Lause<br />
lim (c ⋅ f (x)) = c ⋅ lim f (x) = c ⋅ A,<br />
x→a x→a<br />
lim (f (x) + g(x)) = lim f (x) + lim g(x) = A + B,<br />
x→a x→a x→a<br />
( ) (<br />
lim (f (x) ⋅ g(x)) = lim f (x) ⋅ lim<br />
x→a x→a x→a g(x)<br />
)<br />
= A ⋅ B<br />
f (x)<br />
f (x) B∕=0<br />
lim =<br />
x→a g(x)<br />
lim<br />
x→a<br />
lim<br />
x→a<br />
g(x) = A<br />
B .<br />
(<br />
lim 1 +<br />
x→+∞<br />
1<br />
) x<br />
(<br />
= e, lim 1 +<br />
x<br />
x→−∞<br />
1<br />
) x<br />
= e, lim (1 + x)<br />
x<br />
x→0 1/x = e.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 8 / 24
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Lõpmata väikesed <strong>ja</strong> lõpmata suured suurused<br />
Definitsioon<br />
<strong>Funktsiooni</strong>
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Lõpmata väikesed <strong>ja</strong> lõpmata suured suurused<br />
Definitsioon<br />
<strong>Funktsiooni</strong>
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Lõpmata väikesed <strong>ja</strong> lõpmata suured suurused<br />
Definitsioon<br />
<strong>Funktsiooni</strong>
Lause<br />
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Kahe samas piirprotsessis lõpmata väikese suuruse summa, vahe<br />
<strong>ja</strong> korrutis on samuti lõpmata väike suurus selles piirprotsessis.<br />
Lõpmata väikese suuruse korrutis tõkestatud suurusega on<br />
lõpmata väike suurus.<br />
Kahe samas piirprotsessis lõpmata suure suuruse korrutis on samuti<br />
lõpmata suur suurus.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 10 / 24
Lause<br />
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Kahe samas piirprotsessis lõpmata väikese suuruse summa, vahe<br />
<strong>ja</strong> korrutis on samuti lõpmata väike suurus selles piirprotsessis.<br />
Lõpmata väikese suuruse korrutis tõkestatud suurusega on<br />
lõpmata väike suurus.<br />
Kahe samas piirprotsessis lõpmata suure suuruse korrutis on samuti<br />
lõpmata suur suurus.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 10 / 24
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Kui
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Kui
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Kui piirprotsessis x → a
Lause<br />
<strong>Funktsiooni</strong> <strong>piirväärtus</strong><br />
Kui piirprotsessis x → a
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> f (x) nimetatakse pidevaks punktis a, kui on täidetud kolm<br />
tingimust:<br />
∃f (a);<br />
∃ lim f (x);<br />
x→a<br />
lim f (x) = f (a).<br />
x→a<br />
Tähistatakse f (x) ∈ C(a).<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x), mis ei ole pidev punktis a, nimetatakse katkevaks<br />
punktis a <strong>ja</strong> punkti a nimetatakse funktsiooni f (x) katkevuspunktiks.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 13 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> f (x) nimetatakse pidevaks punktis a, kui on täidetud kolm<br />
tingimust:<br />
∃f (a);<br />
∃ lim f (x);<br />
x→a<br />
lim f (x) = f (a).<br />
x→a<br />
Tähistatakse f (x) ∈ C(a).<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x), mis ei ole pidev punktis a, nimetatakse katkevaks<br />
punktis a <strong>ja</strong> punkti a nimetatakse funktsiooni f (x) katkevuspunktiks.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 13 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> f (x) nimetatakse pidevaks punktis a, kui on täidetud kolm<br />
tingimust:<br />
∃f (a);<br />
∃ lim f (x);<br />
x→a<br />
lim f (x) = f (a).<br />
x→a<br />
Tähistatakse f (x) ∈ C(a).<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x), mis ei ole pidev punktis a, nimetatakse katkevaks<br />
punktis a <strong>ja</strong> punkti a nimetatakse funktsiooni f (x) katkevuspunktiks.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 13 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> f (x) nimetatakse pidevaks punktis a, kui on täidetud kolm<br />
tingimust:<br />
∃f (a);<br />
∃ lim f (x);<br />
x→a<br />
lim f (x) = f (a).<br />
x→a<br />
Tähistatakse f (x) ∈ C(a).<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x), mis ei ole pidev punktis a, nimetatakse katkevaks<br />
punktis a <strong>ja</strong> punkti a nimetatakse funktsiooni f (x) katkevuspunktiks.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 13 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> f (x) nimetatakse pidevaks punktis a, kui on täidetud kolm<br />
tingimust:<br />
∃f (a);<br />
∃ lim f (x);<br />
x→a<br />
lim f (x) = f (a).<br />
x→a<br />
Tähistatakse f (x) ∈ C(a).<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x), mis ei ole pidev punktis a, nimetatakse katkevaks<br />
punktis a <strong>ja</strong> punkti a nimetatakse funktsiooni f (x) katkevuspunktiks.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 13 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Katkevuspunktide liigid<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x) katkevuspunkti a nimetatakse esimest liiki<br />
katkevuspunktiks, kui punktis a eksisteerivad funktsiooni f (x) lõplikud<br />
ühepoolsed <strong>piirväärtus</strong>ed.<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x) katkevuspunkti a, mis ei ole esimest liiki, nimetatakse<br />
teist liiki katkevuspunktiks.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 14 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Katkevuspunktide liigid<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x) katkevuspunkti a nimetatakse esimest liiki<br />
katkevuspunktiks, kui punktis a eksisteerivad funktsiooni f (x) lõplikud<br />
ühepoolsed <strong>piirväärtus</strong>ed.<br />
Definitsioon<br />
<strong>Funktsiooni</strong> f (x) katkevuspunkti a, mis ei ole esimest liiki, nimetatakse<br />
teist liiki katkevuspunktiks.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 14 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Argumendi muut Δx = x − a<br />
<strong>ja</strong> sellele vastav funktsiooni muut<br />
Lause<br />
Δy = f (x) − f (a) = f (a + Δx) − f (a).<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui<br />
Lause<br />
lim Δy = 0.<br />
Δx→0<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui punkti a ümbruses<br />
f (x) on esitatav kujul
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Argumendi muut Δx = x − a<br />
<strong>ja</strong> sellele vastav funktsiooni muut<br />
Lause<br />
Δy = f (x) − f (a) = f (a + Δx) − f (a).<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui<br />
Lause<br />
lim Δy = 0.<br />
Δx→0<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui punkti a ümbruses<br />
f (x) on esitatav kujul
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Argumendi muut Δx = x − a<br />
<strong>ja</strong> sellele vastav funktsiooni muut<br />
Lause<br />
Δy = f (x) − f (a) = f (a + Δx) − f (a).<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui<br />
Lause<br />
lim Δy = 0.<br />
Δx→0<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui punkti a ümbruses<br />
f (x) on esitatav kujul
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Argumendi muut Δx = x − a<br />
<strong>ja</strong> sellele vastav funktsiooni muut<br />
Lause<br />
Δy = f (x) − f (a) = f (a + Δx) − f (a).<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui<br />
Lause<br />
lim Δy = 0.<br />
Δx→0<br />
Funktsioon f (x) on pidev punktis a para<strong>ja</strong>sti siis, kui punkti a ümbruses<br />
f (x) on esitatav kujul
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Pidevate funktsioonide omadusi<br />
Lause<br />
Kui funktsioonid f (x) <strong>ja</strong> g(x) on pidevad punktis a ning b, c ∈ ℝ, siis on<br />
punktis a pidevad ka funktsioonid bf (x) + cg(x) <strong>ja</strong> f (x)g(x) ning<br />
täiendaval tingimusel g(a) ∕= 0 ka funktsioon f (x)/g(x).<br />
Lause<br />
Kui funktsioon g(x) on pidev punktis a <strong>ja</strong> funktsioon f (x) on pidev<br />
punktis g(a), siis liitfunktsioon f (g(x)) on pidev punktis a.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 16 / 24
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
Pidevate funktsioonide omadusi<br />
Lause<br />
Kui funktsioonid f (x) <strong>ja</strong> g(x) on pidevad punktis a ning b, c ∈ ℝ, siis on<br />
punktis a pidevad ka funktsioonid bf (x) + cg(x) <strong>ja</strong> f (x)g(x) ning<br />
täiendaval tingimusel g(a) ∕= 0 ka funktsioon f (x)/g(x).<br />
Lause<br />
Kui funktsioon g(x) on pidev punktis a <strong>ja</strong> funktsioon f (x) on pidev<br />
punktis g(a), siis liitfunktsioon f (g(x)) on pidev punktis a.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 16 / 24
Ühepoolne <strong>pidevus</strong><br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> y = f (x) nimetatakse pidevaks paremalt punktis a, kui<br />
<strong>ja</strong> pidevaks vasakult punktis a, kui<br />
lim Δy = 0<br />
Δx→0+<br />
lim Δy = 0.<br />
Δx→0−<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 17 / 24
Pidevus hulgal<br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> f (x) nimetatakse pidevaks hulgal X ⊆ ℝ, kui ta on pidev<br />
hulga X igas punktis.<br />
Tähistatakse f (x) ∈ C(X).<br />
Lause<br />
Elementaarfunktsioon on pidev oma määramispiirkonna sisepunktides.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 18 / 24
Pidevus hulgal<br />
Definitsioon<br />
<strong>Funktsiooni</strong> <strong>pidevus</strong><br />
<strong>Funktsiooni</strong> f (x) nimetatakse pidevaks hulgal X ⊆ ℝ, kui ta on pidev<br />
hulga X igas punktis.<br />
Tähistatakse f (x) ∈ C(X).<br />
Lause<br />
Elementaarfunktsioon on pidev oma määramispiirkonna sisepunktides.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 18 / 24
Lõigul pidevate funktsioonide omadusi<br />
Lõigul pidevate funktsioonide omadusi<br />
Lause (Weierstrassi teoreem lõigus pideva funktsiooni tõkestatusest)<br />
Lõigul [a, b] pidev funktsioon f (x) on tõkestatud sellel lõigul st. selle<br />
funktsiooni väärtuste hulk sellel lõigul Y = {f (x)∣ x ∈ [a, b]} on<br />
tõkestatud.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 19 / 24
Tõestus.<br />
Lõigul pidevate funktsioonide omadusi<br />
Olgu f (x) ∈ C[a, b]. Eeldame väitevastaselt, et funktsioon f (x) on<br />
tõkestamata sellel lõigul, st suvalise n ∈ ℕ korral leidub selline<br />
xn ∈ [a, b], et ∣f (xn)∣ ⩾ n. Moodustame sel viisil <strong>ja</strong>da {xn}, kusjuures<br />
f (xn) n→∞<br />
→ ∞. Et xn ∈ [a, b], siis <strong>ja</strong>da {xn} on tõkestatud.<br />
Bolzano-Weierstrassi teoreemi põh<strong>ja</strong>l võib tõkestatud <strong>ja</strong>dast {xn}<br />
eraldada koonduva osa<strong>ja</strong>da {xn }. Seega, ∃ lim<br />
k<br />
k→+∞ xn = c ∈ [a, b].<br />
k<br />
Kasutades funktsiooni <strong>pidevus</strong>t lõigul [a, b], leiame, et<br />
lim<br />
k→+∞ f (xn ) = f (c), kusjuures suurus f (c) on lõplik. Teisalt järeldub<br />
k<br />
tingimusest f (xn) n→∞<br />
→ ∞ tingimus f (xn ) k k→∞<br />
→ ∞. Oleme saanud<br />
vastuolu, mis oli tingitud väitevastasest eeldusest. Seega on lõigul<br />
pidev funktsioon tõkestatud sellel lõigul.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 20 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
Hulga ∅ ∕= X ⊂ ℝ vähimat ülemist tõket nimetatakse hulga X<br />
ülemiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse sup X.<br />
Definitsioon<br />
Hulga ∅ ∕= X ⊂ ℝ suurimat alumist tõket nimetatakse hulga X<br />
alumiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse inf X.<br />
Näide: Vahemik X = (0, 1). Leiame inf X <strong>ja</strong> sup X.<br />
Lause (Pidevuse aksioom)<br />
inf X = 0 ∧ sup X = 1.<br />
Igal ülalt tõkestatud reaalarvude hulgal on olemas ülemine ra<strong>ja</strong> <strong>ja</strong> igal<br />
alt tõkestatud reaalarvude hulgal on olemas alumine ra<strong>ja</strong>.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 21 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
Hulga ∅ ∕= X ⊂ ℝ vähimat ülemist tõket nimetatakse hulga X<br />
ülemiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse sup X.<br />
Definitsioon<br />
Hulga ∅ ∕= X ⊂ ℝ suurimat alumist tõket nimetatakse hulga X<br />
alumiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse inf X.<br />
Näide: Vahemik X = (0, 1). Leiame inf X <strong>ja</strong> sup X.<br />
Lause (Pidevuse aksioom)<br />
inf X = 0 ∧ sup X = 1.<br />
Igal ülalt tõkestatud reaalarvude hulgal on olemas ülemine ra<strong>ja</strong> <strong>ja</strong> igal<br />
alt tõkestatud reaalarvude hulgal on olemas alumine ra<strong>ja</strong>.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 21 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
Hulga ∅ ∕= X ⊂ ℝ vähimat ülemist tõket nimetatakse hulga X<br />
ülemiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse sup X.<br />
Definitsioon<br />
Hulga ∅ ∕= X ⊂ ℝ suurimat alumist tõket nimetatakse hulga X<br />
alumiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse inf X.<br />
Näide: Vahemik X = (0, 1). Leiame inf X <strong>ja</strong> sup X.<br />
Lause (Pidevuse aksioom)<br />
inf X = 0 ∧ sup X = 1.<br />
Igal ülalt tõkestatud reaalarvude hulgal on olemas ülemine ra<strong>ja</strong> <strong>ja</strong> igal<br />
alt tõkestatud reaalarvude hulgal on olemas alumine ra<strong>ja</strong>.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 21 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
Hulga ∅ ∕= X ⊂ ℝ vähimat ülemist tõket nimetatakse hulga X<br />
ülemiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse sup X.<br />
Definitsioon<br />
Hulga ∅ ∕= X ⊂ ℝ suurimat alumist tõket nimetatakse hulga X<br />
alumiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse inf X.<br />
Näide: Vahemik X = (0, 1). Leiame inf X <strong>ja</strong> sup X.<br />
Lause (Pidevuse aksioom)<br />
inf X = 0 ∧ sup X = 1.<br />
Igal ülalt tõkestatud reaalarvude hulgal on olemas ülemine ra<strong>ja</strong> <strong>ja</strong> igal<br />
alt tõkestatud reaalarvude hulgal on olemas alumine ra<strong>ja</strong>.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 21 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
Hulga ∅ ∕= X ⊂ ℝ vähimat ülemist tõket nimetatakse hulga X<br />
ülemiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse sup X.<br />
Definitsioon<br />
Hulga ∅ ∕= X ⊂ ℝ suurimat alumist tõket nimetatakse hulga X<br />
alumiseks ra<strong>ja</strong>ks <strong>ja</strong> tähistatakse inf X.<br />
Näide: Vahemik X = (0, 1). Leiame inf X <strong>ja</strong> sup X.<br />
Lause (Pidevuse aksioom)<br />
inf X = 0 ∧ sup X = 1.<br />
Igal ülalt tõkestatud reaalarvude hulgal on olemas ülemine ra<strong>ja</strong> <strong>ja</strong> igal<br />
alt tõkestatud reaalarvude hulgal on olemas alumine ra<strong>ja</strong>.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 21 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
<strong>Funktsiooni</strong> suurimat <strong>ja</strong> vähimat väärtust hulgal nimetatakse<br />
funktsiooni ekstremaalseteks väärtusteks sellel hulgal.<br />
Lause (Weierstrassi teoreem lõigus pideva funktsiooni<br />
ekstremaalsetest väärtustest)<br />
Lõigul pideval funktsioonil on olemas ekstremaalsed väärtused sellel<br />
lõigul.<br />
Lause (Bolzano-Cauchy teoreem vahepealsetest väärtustest)<br />
Lõigul pidev funktsioon omab iga väärtust, mis paikneb<br />
ekstremaalsete väärtuste vahel.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 22 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
<strong>Funktsiooni</strong> suurimat <strong>ja</strong> vähimat väärtust hulgal nimetatakse<br />
funktsiooni ekstremaalseteks väärtusteks sellel hulgal.<br />
Lause (Weierstrassi teoreem lõigus pideva funktsiooni<br />
ekstremaalsetest väärtustest)<br />
Lõigul pideval funktsioonil on olemas ekstremaalsed väärtused sellel<br />
lõigul.<br />
Lause (Bolzano-Cauchy teoreem vahepealsetest väärtustest)<br />
Lõigul pidev funktsioon omab iga väärtust, mis paikneb<br />
ekstremaalsete väärtuste vahel.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 22 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
<strong>Funktsiooni</strong> suurimat <strong>ja</strong> vähimat väärtust hulgal nimetatakse<br />
funktsiooni ekstremaalseteks väärtusteks sellel hulgal.<br />
Lause (Weierstrassi teoreem lõigus pideva funktsiooni<br />
ekstremaalsetest väärtustest)<br />
Lõigul pideval funktsioonil on olemas ekstremaalsed väärtused sellel<br />
lõigul.<br />
Lause (Bolzano-Cauchy teoreem vahepealsetest väärtustest)<br />
Lõigul pidev funktsioon omab iga väärtust, mis paikneb<br />
ekstremaalsete väärtuste vahel.<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 22 / 24
Definitsioon<br />
Lõigul pidevate funktsioonide omadusi<br />
<strong>Funktsiooni</strong> f (x) nimetatakse ühtlaselt pidevaks hulgal X ⊂ ℝ, kui<br />
∀
Lõigul pidevate funktsioonide omadusi<br />
Joone asümptoodid<br />
Definitsioon<br />
Kui joone y = f (x) punkti P kaugenemisel lõpmatusse punkti P<br />
kaugus mingist sirgest läheneb tõkestamatult nullile, siis seda sirget<br />
nimetatakse selle joone asümptoodiks.<br />
vertikaalasümptoodid x = a;<br />
kaldasümptoodid y = kx + b, kus<br />
f (x)<br />
+∞: k = lim<br />
x→+∞ x<br />
f (x)<br />
−∞: k = lim<br />
x→−∞ x<br />
∧ b = lim (f (x) − kx),<br />
x→+∞<br />
∧ b = lim (f (x) − kx).<br />
x→−∞<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 24 / 24
Lõigul pidevate funktsioonide omadusi<br />
Joone asümptoodid<br />
Definitsioon<br />
Kui joone y = f (x) punkti P kaugenemisel lõpmatusse punkti P<br />
kaugus mingist sirgest läheneb tõkestamatult nullile, siis seda sirget<br />
nimetatakse selle joone asümptoodiks.<br />
vertikaalasümptoodid x = a;<br />
kaldasümptoodid y = kx + b, kus<br />
f (x)<br />
+∞: k = lim<br />
x→+∞ x<br />
f (x)<br />
−∞: k = lim<br />
x→−∞ x<br />
∧ b = lim (f (x) − kx),<br />
x→+∞<br />
∧ b = lim (f (x) − kx).<br />
x→−∞<br />
G. Tamberg (TTÜ) YMM3731 Matemaatilne analüüs I 24 / 24