v - FSB

MEHANIKA FLUIDA II – Što valja zapamtiti 1 

MATEMATIČKE OSNOVE 

Vrijedi pogledati prvi i polovinu drugog sažetka iz Mehanike fluida I. 

Svaki tenzor drugog reda se može prikazati zbrojem simetričnog i antisimetričnog 

tenzora. 

1 1 

Tij= ( Tij + Tji) + ( Tij − Tji) = Sij + Aij 

�� 2 �� 2 

Sij = Sji Aij =−Aji 

1 1 

T = T+ T + T− T = S+ A 

�� 2 �� 2 

T T 

ili ( ) ( ) 

T T 

S= S A=−A Simetrični dio je polovina zbroja tenzora T i transponiranog tenzora T T , dok je 

antisimetrični dio jednak polovini njihove razlike. Primjer: 

6 0 4 6 4 3 0 −4 

1 

8 1 7 = 4 1 1 + 4 0 6 

2 −5 3 

�� 

3 1 3 

�� 

−1 −6 

0 

�� 

Tij Sij Aij 

Dualni vektor tenzora drugog reda 

Svakom se tenzoru drugog reda zadanom komponentama Tjk može pridružiti dualni vektor 

di, definiran izrazom: 

di= εijkTjk 

Ako se tenzor prikaže zbrojem simetričnog i antisimetričnog dijela, uzimajući u obzir da je 

umnožak permutacijskog simbola sa simetričnim dijelom jednak nuli (jer je dvostruki 

skalarni produkt simetričnog i antisimetričnog tenzora jednak nuli) zaključuje se da se 

gornja definicija može pisati i u obliku: 

d = ε A 

i ijk jk 

gdje je Aij antisimetrični dio tenzora Tij. 

Ako se gornji izraz pomnoži s εilm, te umnožak εijkεilm zamijeni umnoškom Kroneckerovih 

simbola dobije se: 

1 

Alm = εilmdi 

2 

Dakle, svaki se tenzor može prikazati s pomoću simetričnog i antisimetričnog dijela ili s 

pomoću simetričnog dijela i dualnog vektora u obliku: 

1 

Tij= Sij + Aij = Sij + εkijdk 

2 

Sferni i devijatorski dio tenzora drugog reda 

Svaki se tenzor drugog reda može prikazati kao zbroj sfernog i devijatorskog dijela tenzora 

u obliku: 

1 

Tij = Tkkδij+ Σ ij 

3


gdje je prvi član desne strane sferni dio, a drugi devijatorski dio tenzora. Očito da je Tkk 

skalar, pa je sferni dio izotropni tenzor, kojemu se pri rotaciji koordinatnog sustava 

komponente ne mijenjaju. Devijatorski dio tenzora se računa kao razlika samog tenzora i 

njegova sfernog dijela. Kontrakcijom indeksa u gornjem izrazu slijedi da je Σjj=0 (suma 

članova na glavnoj dijagonali devijatorskog dijela tenzora je nula). 

Primjer: 

8 5 −1 4 0 0 4 5 −1 

5 4 2 = 0 4 0 + 5 0 2 

−1 2 0 0 0 4 −1 2 −4 

Laplaceov (delta) operator 

Laplaceov ili delta operator definiran je kao divergencija gradijenta i označava se sa Δ. 

Primjenom Laplaceova operatora na skalarno polje dobije se: 

2 

∂ Φ 

ΔΦ = div(grad Φ) =∇⋅( ∇ Φ) 

= 

∂xi∂ xi 

Delta operator se dakle može zapisati u obliku: 

2 

∂ • 

2 

∂ • 

2 

∂ • 

2 

∂ • 

xi xi 2 

x1 2 

x2 2 

x3 

Δ•= 

∂ ∂ 

= 

∂ 

+ 

∂ 

+ 

∂ 

gdje umjesto oznake “• ” može stajati skalarno, vektorsko ili tenzorsko polje. 

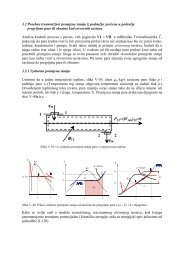
Prostorna krivulja i krivuljni integral 

Slika 1. prikazuje krivulju C omeđenu točkama A i B. Jedan od načina analitičkog 

zadavanja krivulje je parametarski, u kojem se položaj svake točke na krivulji opisuje 

vektorom položaja koji je funkcija parametra t, u obliku: 

� � � � 

r t = x t e + x t e + x t e 

( ) ( ) ( ) ( ) 

1 1 2 2 3 3 

Povećavajući vrijednost parametra t u granicama tA (vrijednost parametra u točki A) do tB 

dobivaju se sve točke krivulje C, 

omeđene točkama A i B. Ako su točke 

x1 

A 

x3 

O 

r (t) 

� 

� � � � 

d s = r ( t + dt) 

− r ( t) 

= dr 

� 

r ( t + dt) 

x2 

Slika 1. Usmjereni element krivulje 

B 

A i B iste, krivulja je zatvorena. 

Usmjereni element ds � krivulje C 

orijentiran je u smjeru porasta 

parametra t i odgovara razlici vektora 

položaja kao što je definirano na slici 1. 

Komponente elementarnog vektora ds � 

u indeksnoj notaciji su: 

� � � � � 

ds= dxe = dxe+ dxe+ dxe 

j j 

1 1 2 2 3 3 

Krivuljni integral vektorskog polja v � 

po orijentiranoj krivulji C, obrubljenoj 

točkama A i B, definiran je izrazom: 

B B 

� � 

v⋅ ds = v dx 

∫ ∫ 

A A 

j j


Tako se npr. u mehanici rad polja sile na putu duž krivulje C, opisuje krivuljnim 

integralom, koji se još naziva hod u polju sile duž krivulje C. Krivuljni integral po 

jednostavno zatvorenoj krivulji C (krivulja koja nema samopresjecišta) nosi naziv ophod 

ili cirkulacija, a označuje se u obliku: 

� � 

�∫ v⋅ ds = vjdx C � ∫C 

j 

Ako je v � polje brzine gornji izraz označuje cirkulaciju brzine po zatvorenoj krivulji C. 

Bezcirkulacijsko vektorsko polje 

Vektorsko polje v � je bezcirkulacijsko (bezophodno) ako je cirkulacija po bilo kojoj 

jednostavno zatvorenoj krivulji C u području polja v � , jednaka nuli, tj. vrijedi: 

v dx = 0 

∫� 

C 

j j 

Konzervativno vektorsko polje 

Vektorsko polje v � je konzervativno ako krivuljni integral između točaka A i B ne zavisi 

od krivulje koja spaja te točke. Lako se može pokazati da je vektorsko polje 

bezcirkulacijsko ako i samo ako je konzervativno. 

Potencijalno vektorsko polje 

Svako vektorsko polje koje se može prikazati s pomoću gradijenta skalarnog polja Φ u 

obliku: 

� 

∂Φ 

v = grad Φ ili vj= 

∂x 

j 

naziva se potencijalnim poljem, kojemu je polje Φ skalarni potencijal. Svako potencijalno 

polje je konzervativno i bezophodno, jer je krivuljni integral duž krivulje obrubljene 

točkama A i B jednak: 

B B B 

∂Φ 

∫vjdxj = ∫ dxj = dΦ = Φ( B) 

−Φ( 

A) 

∂x 

∫ 

A A j A 

Iz gornjeg izraza je jasno da se za slučaj potencijalnog polja podintegralna funkcija svodi 

na potpuni diferencijal, te je vrijednost krivuljnog integrala jednaka razlici potencijala u 

točkama B i A i ne zavisi od spojnice točaka A i B, što je po definiciji svojstvo 

konzervativnih polja. Ako je krivulja zatvorena, što znači da se točke A i B poklapaju, 

jasno je da će i cirkulacija potencijalnog polja biti jednaka nuli, što je osobina 

bezcirkulacijskog polja. Dakle potencijalno polje je konzervativno, odnosno 

bezcirkulacijsko. 

Bezvrtložno vektorsko polje 

Bezvrtložno vektorsko polje je ono kojemu je rotor polja jednak nuli, tj. 

� 

∂vk 

rotv = 0 ili εijk = 0 

∂x 

j 

Lako se pokaže da je rotor potencijalnog polja nul vektor, jer je: 

� 

∂ ⎛∂Φ⎞ ( rotv ) = ( rot ( gradΦ ) ) = εijk 0 

i i ⎜ ⎟= 

∂xj ⎝∂xk �� 

⎠ 

simetrično 

pa se zaključuje da su pojmovi potencijalnosti i bezvrtložnosti polja v � ekvivalentni. 

Solenoidalno vektorsko polje


Za vektorsko polje kojemu je divergencija identički jednaka nuli ( divv � =0), kaže se da je 

bezizvorno ili solenoidalno. Svako polje brzine u nestlačivom strujanju je bezizvorno, jer 

zadovoljava jednadžbu kontinuiteta oblika divv � =0. 

Svako bezizvorno polje se može prikazati s pomoću rotora nekog drugog vektorskog polja, 

koje se naziva vektorskim potencijalom. Ako je polje ψ � vektorski potencijal polja v � , tada 

vrijedi: 

� � 

∂ψ 

k 

v = rot ψ ili vi 

= εijk ∂x 

j 

Jasno je da je divergencija polja v � jednaka nuli, jer je div(rotψ � )=0, što je u indeksnom 

zapisu očito: 

2 

� ∂vi ∂ ⎛ ∂ψ ⎞ 

k ∂ψk 

divv = = ⎜εijk ⎟= 

εijk = 0 

∂xi ∂x ⎜ 

i x ⎟ 

⎝ ∂ j ⎠ ∂xj∂xi �� 

simetrično 

2 

∂ ψ k 

jer je permutacijski simbol antisimetričan u odnosu na indekse i i j, dok je tenzor 

∂xj∂ xi 

simetričan u odnosu na te iste indekse, zbog pravila o zamjeni redoslijeda deriviranja, a 

prema poznatom pravilu produkt simetričnog i antisimetričnog tenzora jednak je nuli. 

Budući da je rotor potencijalnog vektorskog polja jednak nuli, za zadano vektorsko polje 

v � vektorski je potencijal ψ � neodređen do na gradΦ (jer je rot(ψ � +gradΦ )=rotψ � ). Stoga 

će se svako vektorsko polje moći prikazati zbrojem svoga potencijalnog i solenoidalnog 

dijela u obliku 

� 

� ∂Φ ∂ψ 

k 

v = gradΦ + rot ψ ili vi 

= + εijk 

∂x ∂x 

i j


DODATAK IZ KINEMATIKE FLUIDA 

Nastavak na sažetak 6 iz Mehanike fluida I 

Prvi Helmholtzov teorem 

Gibanje krutog tijela (kod kojeg je relativni međusobni položaj čestica stalan) moguće je 

prikazati zbrojem translatornog i sfernog (ili rotacijskog) gibanja. Za razliku od krupog 

tijela, fluid je tvar koja se pod djelovanjem ma kako malog smičnog naprezanja neprekidno 

deformira, pa je za očekivati da će u strujanju fluida relativni međusobni položaj čestica 

fluida biti promjenjiv. 

Prirast brzine u dvije vrlo bliske točke prostora opisuje se pomoću gradijenta brzine u 

obliku 

∂vi 

dvi = dxj 

∂x 

j 

Gradijent brzine je tenzor drugog reda koji se može prikazati zbrojem simetričnog D ij i 

antisimetričnog ij V dijela, odnosno preko simetičnog dijela i dualnog vektora Ω k u obliku 

∂ vi 

1 

= D + V = D + ε 

∂x 

2 

j 

Ω 

ji ji ji kji k 

Tenzor brzine deformacije 

Simetrični dio D ij tenzora gradijenta brzine naziva se tenzorom brzine deformacije, a 

definiran je izrazom 

1⎛ ∂v 

∂v 

⎞ 

i j 

1 � T � 

Dji = ⎜ + ⎟ ili u simoličkom zapisu D = ( gradv+ grad v) 

2⎜∂xj ∂x 

⎟ 

⎝ i ⎠ 

2 

Tablični prikaz komponenti tenzora brzine deformacije, koji ima šest različitih komponenti 

je 

∂v1 1 ⎛ ∂v2 ∂v ⎞ 1 1 ⎛ ∂v3 

∂v 

⎞ 1 

⎜ + ⎟ ⎜ + ⎟ 

∂x1 2 ⎝ ∂x1 ∂x2 ⎠ 2 ⎝ ∂x1 ∂x3 

⎠ 

1 ⎛ ∂v1 ∂v ⎞ 2 ∂v2 1 ⎛ ∂v3 

∂v 

⎞ 2 

D ji = ⎜ + ⎟ 

⎜ + ⎟ 

2 ⎝ ∂x2 ∂x1 ⎠ ∂x2 2 ⎝ ∂x2 ∂x3 

⎠ 

1 ⎛ ∂v1 ∂v ⎞ 3 1 ⎛ ∂v2 

∂v ⎞ 3 ∂v3 

⎜ + ⎟ ⎜ + ⎟ 

2 ⎝ ∂x3 ∂x1 ⎠ 2 ⎝ ∂x3 ∂x2 ⎠ ∂x3 

Ako se u određenom trenutku t uoči elementarni volumen fluida oblika paralelopipeda 

kojemu su duljine bridova dx 1, 

dx 2 i dx 3 , tada će u vremenskom trenutku t+ dt 

taj 

paralelopiped promijeniti položaj (uslijed translacije i rotacije), ali i oblik uslijed 

deformacije. Deformacija tog paralelopipeda se očituje kroz promjene duljina njegovih 

bridova i kroz promjenu kuta među njegovim bridovima. Članovi na glavnoj dijagonali 

tenzora brzine deformacije označuju brzine relativne promjene duljine bridova, tj. vrijedi: 

∂v1 

1 Dd ( x1 

) 

D11 

= = 

, gdje je 

∂x 

dx Dt 

D 

operator materijalne derivacije. Vrijedi i 

Dt 

1 1


( x ) 

( ) 

∂v2 

1 Dd 2 ∂v3 

1 Ddx3 

D22 

= = 

i D33 

= = 

∂x2 

dx2 Dt 

∂x3 

dx3 Dt 

Brzina relativne promjene obujma dV = dx1dx2dx3 elementa fluida je definirana izrazom 

1 D( dV) 1 D( dx1dx2dx3) ∂v 

j � 

= = D11+ D22 + D33 = = divv 

dV Dt dx1dx2dx3 Dt 

∂xj 

U nestlačivom strujanju fluida je gustoća fluida konstantna, pa nema promjene volumena 

∂v 

j � 

čestica fluida što znači da mora biti = divv = 0 . 

∂x 

j 

Članovi izvan glavne dijagonale govore o brzini kutne deformacije, tj. o brzini smanjenja 

kuta među bridovima početnog elementarnog paralelopipeda. Tako bi npr. vrijedilo 

Dθ12 

∂v2∂v1 = 2D12 = 2D21 

= + , 

Dt 

∂x ∂x 

1 2 

gdje je θ 12 kut između bridova dx 1 i 2 

ostale komponente. 

dx iz početne konfiguracije. Analogno vrijedi i za 

Tenzor vrtložnosti 

Antisimetrični dio tenzora gradijenta brzine se naziva tenzorom vrtložnosti, a definiran je 

izrazom: 

1⎛ ∂v 

∂v 

⎞ 

i j 

Vji = ⎜ − 

2⎜ ⎟ 

xj x ⎟ 

⎝∂ ∂ i ⎠ 

ili u simoličkom zapisu 

1 � T � 

V = ( gradv−grad v) 

2 

Tablični prikaz komponenti tenzora vrtložnosti, koji ima tri po apsolutnoj vrijednosti 

različite komponente je 

0 

1 ⎛ ∂v2 ⎜ 

2 ⎝ ∂x1 ∂v1 − 

∂x2 ⎞ 

⎟ 

⎠ 

1 ⎛ ∂v3 

⎜ 

2 ⎝ ∂x1 ∂v1 

− 

∂x3 

⎞ 

⎟ 

⎠ 

V ji = 

1 ⎛ ∂v1 ⎜ 

2 ⎝ ∂x2 ∂v2 − 

∂x1 ⎞ 

⎟ 

⎠ 

0 

1 ⎛ ∂v3 

⎜ 

2 ⎝ ∂x2 ∂v2 

− 

∂x3 

⎞ 

⎟ 

⎠ 

1 ⎛ ∂v1 ⎜ 

2 ⎝ ∂x3 ∂v3 − 

∂x1 ⎞ 

⎟ 

⎠ 

1 ⎛ ∂v2 

⎜ 

2 ⎝ ∂x3 ∂v3 

− 

∂x2 

⎞ 

⎟ 

⎠ 

0 

Vektor vrtložnosti 

Vektor vrtložnosti je u matematičkom smislu dualni vektor tenzora gradijenta brzine, 

odnosno tenzora vrtložnosti, a definiran je izrazom: 

∂v 

� 

i 

� 

Ωk = εkji = εkjiVji ili Ω = rotv 

∂x 

j 

U fizikalnom smislu vektor vrtložnosti odgovara dvostrukoj vrijednosti vektora kutne 

brzine ω � � � 

( Ω = 2ω) 

kojom rotira čestica fluida. Kod krutog tijela vektor kutne brzine je 

jedan te isti za sve čestice tijela, dok pri strujanju fluida on može biti različit za svaku 

česticu fluida. Strujanje fluida kod kojega je vektor vrtložnosti identički jednak nuli 

� 

( rotv = 0 ) je po definiciji bezvrtložno, odnosno potencijalno strujanje. 

Komponente tenzora vrtložnosti mogu se prikazati preko komponenti vektora vrtložnosti 

ili komponenata vektor kutne brzine rotacije, u obliku 

1 

V ji = εkjiΩk= εkjiωk 

2


Ako se u polaznom izrazu za prirast brzine dvi = vBi − vAi 

u dvije bliske točke A i B 

(udaljene za dx j ) gradijent brzine prikaže s pomoću tenzora brzine deformacije i vektora 

kutne brzine, dobije se izraz za brzinu u točki B izraženu s pomoću brzine u točki A 

vBi = v 

�Ai 

+ Djidxj + εikjωkdxj �� 

translacija deformacija sferno gibanje 

Gornji izraz označuje sadržaj prvog Helmholtzovog teorema koji kaže da se gibanje dviju 

bliskih točaka kontinuuma može prikazati zbrojem translacijskog i sfernog gibanja (kao 

kod krutog tijela) te deformacijskog gibanja. 

Jasno je da ako se fluid giba bez deformacija, da je to gibanje poput krutog tijela. Primjer 

takva gibanja je rotacija fluida zajedno s posudom oko vertikalne osi (slučaj relativnog 

mirovanja obrađen u MF I). 

Druga posebna klasa strujanja je ona kod koje nema rotacije čestica fluida, što znači da su 

vektori kutne brzine, odnosno vektor vrtložnosti, odnosno rotv � jednaki nuli. Kao što je 

prije rečeno (vidjeti sažetak prvih predavanja) vektorsko polje kojemu je rotor jednak nuli 

se naziva bezvrtložnim ili potencijalnim poljem, a koje je onda i bezcirkulacijsko i 

konzervativno. Takvo se polje može prikazati gradijentom skalarnog potencijala 

� 

v = gradϕ 

. Stoga će se i strujanje u kojem nema rotacija čestica fluida zvati potencijalnim 

strujanjem. 

OSNOVE NESTLAČIVOG POTENCIJALNOG STRUJANJA 

Primijećeno je da model potencijalnog strujanja fluida vrijedi u uvjetima kod kojih se 

viskozne sile mogu zanemariti. Bezvrtložno strujanje se pojavljuje npr. pri opstrujavanju 

tijela i to u području podalje od stijenke (gdje je utjecaj viskoznih sila zanemariv). 

Strujanje fluida koje nastaje pri samom početku gibanja tijela u mirujućoj tekućini, također 

se može opisati potencijalnim poljem brzine. U tehničkoj praksi se model potencijalnog 

strujanja primjenjuje u slučajevima u kojima su viskozne sile minorne u odnosu na 

inercijske i gravitacijske sile. Tipične primjene modela potencijalnog strujanja su u 

aerodinamici i teoriji turbostrojeva za određivanje sile uzgona pri optjecanju aeroprofila, te 

u brodogradnji npr. za određivanje otpora valova gibajućeg broda i u analizi ponašanja 

plivajućih struktura na valovima. 

Nestlačivo strujanje opisano je jednadžbom kontinuiteta 

∂v 

j 

= 0 

∂x 

j 

i jednadžbom količine gibanja (II. Newtonovim zakonom) u kojoj su zanemarene viskozne 

sile (vidjeti npr. sažetak 3. predavanja iz MFI) 

∂vi ∂vi ∂p 

ρai = ρ + ρvj = ρ fi 

− . 

∂t ∂xj ∂xi 

Ako masena sila odgovara sili gravitacije, tada se ona može prikazati preko potencijala, 

∂ρ 

gx3 

koji za slučaj da je os x 3 usmjerena vertikalno uvis, glasi ρ fi =− ρgδi3=− . 

∂xi 

Sustav gornje dvije jednadžbe (često se nazivaju i Eulerove jednadžbe) označuje sustav 

parcijalnih diferencijalnih jednadžbi prvog reda, a opisuje neviskozno strujanje fluida (koje 

može biti i vrtložno). Jednadžba kontinuiteta je linearna jednadžba, a jednadžba količine


∂vi 

gibanja je nelinearna zbog člana ρv 

j . Zbog nelinearnosti jednadžbe količine gibanja 

∂x 

j 

ovaj se sustav može riješiti samo numeričkim putem. Uz pretpostavku potencijalnog 

strujanja, u kojem vrijedi 

∂ϕ 

v j = 

∂x 

j 

jednadžba kontinuiteta prelazi u Laplaceovu jednadžbu 

2 2 2 

∂v j ∂ ⎛ ∂ϕ ⎞ 

∂ ϕ ∂ ϕ ∂ ϕ 

= ⎜ ⎟= 

0 ili Δ ϕ= 

+ + = 0 

2 2 2 

∂xj ∂x ⎜ 

j x ⎟ 

⎝ ∂ j ⎠ 

∂x1 ∂x2 ∂x3 

Nelinearni član u jednadžbi količine gibanja prelazi u 

2 

∂vi ∂ϕ ∂ ⎛ ∂ϕ ⎞ ∂ϕ ∂ ⎛ ∂ϕ ⎞ ∂ ⎛ ρ ∂ϕ ∂ϕ ⎞ ∂ ⎛ ρv⎞ 

ρvj= ρ ⎜ ⎟= ρ ⎜ ⎟= ⎜ ⎟= 

⎜ ⎟ 

∂xj ∂xj ∂xj xi xj x ⎜ 

i x ⎟ 

j x ⎜ 

i 2 xj x ⎟ 

⎝ ∂ ⎠ ∂ ∂ ⎝ ∂ ⎠ ∂ ⎝ ∂ ∂ j ⎠ ∂xi ⎝ 2 ⎠ 

pa jednadžba količine gibanja prelazi u oblik 

2 

∂ ⎡ ∂ϕ 

ρv 

⎤ 

⎢ρ + + ρgx3 

+ p⎥ 

= 0 

xi⎣ ∂t 

2 

⎦ 

Zbroj u uglatoj zagradi očito nije funkcija prostornih koordinata, pa vrijedi izraz (koji je 

poznat pod nazivom Euler-Bernoullijeva jednadžba) 

2 

∂ϕ 

ρv 

ρ + + ρgx3+ 

p= f () t 

∂t 

2 

gdje je f () t neka funkcija vremena. 

Za slučaj stacionarnog potencijalnog strujanja polazni sustav jednadžbi je 

2 2 2 2 

∂ ϕ ∂ ϕ ∂ ϕ ∂ ϕ 

= + + = 0 

2 2 2 

∂x ∂x ∂x ∂x ∂x 

j j 

1 2 3 

2 

ρv 

+ ρgx3 

+ p = C = konst. 

2 

Osnovna prednost ovog sustava jednadžbi koji opisuje neviskozno bezvrtložno strujanje je 

u činjenici, da je nelinearna jednadžba količine gibanje prešla u algebarsku jednadžbu, te 

se gornji sustav jednadžbi rješava tako da se prvo riješi jednadžba kontinuiteta, čime je 

određeno polje brzine, a zatim se iz druge jednadžbe (koja je oblika Bernoullijeve 

jednadžbe) odredi polje tlaka. Treba naglasiti da je u gornjoj jednadžbi konstanta C 

jedna te ista za cijelo područje strujanja (ne za strujnicu kao kod Bernoullijeve 

jednadžbe) pa se jednadžba može postavljati između bilo koje dvije točke u području 

strujanja, ne vodeći računa o strujnicama. Laplaceova jednadžba je linearna parcijalna 

diferencijalna jednadžba, koja se za slučaj stacionarnoga strujanja rješava uz zadane rubne 

uvjete. Tipični rubni uvjet na stjenci optjecanog tijela je uvjet nepromočivosti stjenke, tj. 

normalna komponenta brzine na stjenci mora biti jednaka brzini stjenke. 

Za primjer prema slici, gdje fluid nastrujava na 

n 

mirujuće tijelo, vrijedi na površini tijela 

∂ϕ∂ϕ vn = vjnj = nj 

= = 0 

∂xj∂n Dovoljno daleko od tijela, utjecaj tijela se ne 

osjeća, pa je potencijal jednak potencijalu 

neporemećenog strujanja ϕ = ϕ∞ . 

�


Osnovna svojstva rješenja Laplaceove jednadžbe 

(1) Princip superpozicije. S obzirom da je Laplaceova jednadžba linearna, vrijedi 

princip superpozicije (ili zbroj dvaju rješenja Laplaceove jednadžbe također je 

rješenje Laplaceove jednadžbe). 

( 1) 

( 2) 

Ako potencijali ϕ i ϕ zadovoljavaju Laplaceovu jednadžbu onda je jasno da je zbroj 

(1) (2) 

ϕ = ϕ + ϕ također rješenje Laplaceove jednadžbe jer vrijedi 

( ϕ ϕ ) 

∂ + 

2 (1) (2) 

∂x ∂x 

j j 

2 

∂ ϕ 

= 

∂x ∂x 

j j 

= 0 

- isto vrijedi i za brzine: 

(1) 

(2) 

(1) ∂ϕ 

(2) ∂ϕ 

∂ϕ 

(1) (2) 

vi 

= ; vi 

= ; vi = = vi + vi 

∂xi 

∂xi 

∂xi 

Dakle brzine uzrokovane dvama potencijalima se zbrajaju. 

(1) (2) 

Oprez! To ne vrijedi za tlakove p ≠ p + p jer je tlak definiran nelinearnom 

jednadžbom. 

(2) Potencijal ne može imati niti maksimum niti minimum unutar područja, nego samo 

po rubu. 

rub 

Slika prikazuje područje V opasano 

rubom S unutar kojeg je definiran 

n j potencijal brzine koji zadovoljava 

Δ V 

Δ S 

S 

2 

∂ ϕ 

Laplaceovu jednadžbu 

∂xj∂xj = 0 . 

područje M 

Integriranjem Laplaceove jednadžbe po 

volumenu V uz primjenu Gaussove 

V 

formule slijedi 

2 

∂ ϕ 

∫ ∂x ∂x ∂ϕ ∂ϕ 

dV = ∫ n jdS 

= dS = 0 

∂x ∫ ∂n 

j j s j 

s 

∂ϕ 

Pretpostavimo da je u točki M lokalni maksimum, tada bi bio pozitivan za sve točke 

∂n 

površine ΔS koja okružuje točku M, pa bi ∫ dS 

n Δs ∂ 

∂ϕ 

>0 što je u suprotnosti s Laplaceovom 

jednadžbom. Slično vrijedi i za pretpostavku minimuma u točki M. 

(3) Brzina strujanja također ne može imati ekstrem unutar područja strujanja 

Deriviranjem Laplaceove jednadžbe 

2 

∂ ϕ 

∂x ∂x 

j j 

= 0 

sve što vrijedi za ϕ vrijedi i za komponente brzine k 

po x k slijedi 

v . 

2 

∂ vk 

∂x ∂x 

j j 

= 0 , pa je jasno da


(4) Polje brzine u potencijalnom strujanju je bezcirkulacijsko (cirkulacija brzine po 

zatvorenoj krivulji jednaka je nuli) jer je: 

∂ϕ 

Γ = ∫ v jdx 

j = ∫ dx j = = 0 

∂ ∫ dϕ 

x 

C 

C j 

C 

Strujna funkcija (funkcija toka) u ravninskom strujanju 

U ravninskom strujanju se slika strujanja ponavlja u međusobno paralelnim ravninama npr. 

∂ 

paralelnim s 0x1x 2, 

pa vrijedi v3 ≡ 0 i = 0 . 

∂x 

x2 

0 

3 

Slika prikazuje strujnice u ravninskom potencijalnom strujanju. Vektor brzine v i je po 

definiciji kolinearan s lukom strujnice dx i i okomit na krivulje ϕ = konst. (jer je 

� 

v = gradϕ 

). Uvodimo strujnu funkciju (funkciju toka) ψ sa svojstvom da ψ = konst. 

dx1 označuje strujnicu. Iz jednadžbe strujnice 

v1 = 

dx2 

v2 

slijedi v 

�1 dx2 − v 

�2 

dx1 

= 0 

∂ψ ∂ψ 

∂x2 ∂x1 

�� 

∂ψ 

Ako je v1 

= 

∂x 

2 

i v2 

∂ψ 

=− 

∂x 

znači da će na strujnici biti konst. 

2 1 

1 

dψ= 

0→ ψ= 

konst. 

, onda će jednadžba strujnice prijeći u oblik dψ = 0 , što 

ψ = S obzirom da je j 

potencijala brzine ϕ i funkcije toka ψ 

∂ϕ∂ψ v1 

= = 

∂x1 ∂x2 

ili u polarnim koordinatama 

∂ϕ∂ψ v2 

= =− 

v 

∂x∂x v 

i 

ϕ = konst. 

Gornje relacije su poznate pod nazivom Cauchy-Riemanovi uvjeti. 

v r 

ϑ 

v 

strujnica: 

ψ = konst. 

x 1 

∂ϕ 

= , slijedi veza između 

∂x 

∂ϕ 

1 ∂ψ 

= = 

∂r 

r ∂ϑ 

1 ∂ϕ 

∂ψ 

= = − 

r ∂ϑ 

∂r 

j


Veza između funkcije toka i protoka fluida između dvije strujnice 

Slika prikazuje dvije strujnice u ravninskom strujanju (prostorno gledajući to su dvije 

strujne površine). Prema jednadžbi kontinuiteta u nestlačivom strujanju protok između 

dvije strujne površine je konstantan. Ako se protok izrazi po jedinici duljine okomito na 

ravninu slike, onda je protok kroz krivulju � AB definiran izrazom 

B 

Q= ∫ vn i ids 

A 

Ako elementarni luk ds čini s osi x 1 kut α tada su komponente jediničnog vektora 

n , n = (sin α, − cos α) 

, pa se komponente vektora nds mogu izraziti u obliku 

normale ( ) 

1 2 

nd s = (d x , − d x ) , što uvršteno u izraz za protok daje 

i 

x2 

0 

Q 

2 1 

B B B 

B 

ds 

A 

strujnica: 

k 

Q= ∫vn i ids 

= ∫ v dx − v dx = d 

� � ∫ ψ = ψ ( B) − ψ ( A) 

= K −K 

n i 

strujnica: 

k 

1 2 2 1 2 1 

A A ∂ψ ∂x2 ∂ψ 

− 

∂x1 

A 

v i 

Kao što se i očekivalo, protok Q ne zavisi od izbora položaja točaka A i B na strujnicama, 

jer je jednak razlici vrijednosti funkcije toka na tim strujnicama. 

x 1 

i

x1 

x1 

x3 

σ11 

O 

x3 

σ 31 


DINAMIKA FLUIDA 

Vrijedi pogledati i sažetak 2 iz Mehanike fluida I (sile u fluidu) 

σ 13 

n j 

S 

σ12 

σ 33 

x2 

σ 21 

σ 32 

σ 23 

idS σ 

V 

fidm σ22 

x2 

fi 

Masene sile su posljedica položaja mase u 

f masene sile. Masena sila F na 

polju i 

d i 

česticu fluida: d Fi = fidm= ρ fidV Potencijalne masene sile su one koje se 

mogu prikazati gradijentom skalarne 

∂U 

funkcije U: fi 

= − . 

∂ xi 

Površinske sile su sile dodira između 

čestica fluida ili između čestica fluida i 

stijenke. Definirane su vektorom naprezanja 

σi . Sila dFi na elementarnu površinu d S : 

d Fi= σidS. 

Stanje naprezanja u točki prostora 

jednoznačno je definirano tenzorom 

naprezanja. Tablični zapis komponenti 

tenzora naprezanja 

ji 

↓ 

j 

→i 

(smjer) 

σ σ σ 

11 12 13 

σ = σ σ σ 

21 22 23 

σ σ σ 

31 32 33 

gdje se indeks j odnosi na površinu. 

Veza između vektora i tenzora naprezanja: 

σ ( n ) n σ 

i j = j ji 

Osnovni zakoni dinamike fluida 

Dinamika plinova se temelji na osnovnim zakonima klasične fizike u koje spadaju 

1. Zakon očuvanja mase, 

2. Zakon očuvanja količine gibanja, 

3. Zakon očuvanja momenta količine gibanja, 

4. Zakon očuvanja energije, 

5. Drugi zakon termodinamike. 

Zakoni količine gibanja i momenta količine gibanja su konceptualno definirani u klasičnoj 

mehanici, a posljednja dva u termodinamici. Ovi su zakoni definirani za sustav 

materijalnih točaka odnosno za zatvoreni termodinamički sustav, a u dinamici fluida će biti 

primijenjeni na materijalni volumen VM(t), koji će u općem slučaju s vremenom mijenjati 

svoj položaj, oblik i veličinu, ali će se uvijek sastojati od jednih te istih čestica fluida. 

Strujanja fluida se mogu podijeliti na nestlačiva (u kojima je gustoća fluida konstantna, 

uglavnom su to strujanja kapljevina) i stlačiva strujanja (strujanja plinova pri većim 

brzinama u usporedbi s brzinom zvuka). Pri nestlačivom strujanju volumeni čestica fluida


ostaju konstantni, što znači da se čestice fluida ne mogu komprimirati (pri čemu bi se 

povećala unutarnja energija fluida na račun rada kompresije) niti ekspandirati (pri čemu bi 

se dobio mehanički rad na račun unutarnje energije), što znači da će se mehanička energija 

pretvarati u unutarnju samo putem viskoznih sila, što je jednosmjeran proces. U kolegiju 

Mehanika fluida I, smo se bavili samo nestlačivim gibanjem, te smo u modificiranoj 

Bernoullijevoj jednadžbi pretvorbu mehaničke energije u unutarnju nazivali gubicima 

mehaničke energije, jer se jednom pretvorena mehanička energija više ne može povratiti iz 

unutarnje energije nestlačivog fluida. Unutar ovog kolegija ćemo definirati općenitiji 

model stlačivog strujanja u kojem postoji dvosmjerni proces pretvorbe iz mehaničke 

energije u unutarnju i obrnuto, te u energijsku jednadžbu moramo uključiti i unutarnju 

energiju, koja je definirana u prvom zakonu termodinamike, te ćemo prije nego definiramo 

osnovne zakone dinamike fluida načiniti kratak pregled osnovnih termodinamičkih 

relacija, te naglasiti specifičnosti njihove primjene u opisu strujanja fluida. U Mehanici 

fluida I smo se bavili integralnim pristupom, a ovdje ćemo dati naglasak na diferencijalni 

pristup, koji je osnova za računalnu dinamiku fluida, danas sve rašireniji pristup rješavanju 

problema strujanja fluida i popratnih pojava. 

Koncept iz termodinamike 

Termodinamički sustav i materijalni volumen 

Termodinamički sustav je volumen ispunjen materijom koji je granicom odijeljen od 

okoline. Granica može biti svaka geometrijski zatvorena površina (stvarna ili zamišljena) s 

definiranim svojstvima u svakoj njenoj točki. Granica može biti nepomična ili pomična, 

toplinski provodljiva ili neprovodljiva (adijabatska), a također propusna za masu (kada se 

govori o otvorenom sustavu) ili nepropusna za masu (kada se govori o zatvorenom 

sustavu). Materijalni volumen u mehanici fluida je primjer zatvorenog termodinamičkog 

sustava, te će se daljnja razmatranja ograničiti na takve termodinamičke sustave. 

Ravnotežno stanje termodinamičkog sustava i veličine stanja 

Svaki zatvoreni termodinamički sustav, prepušten sam sebi (bez izmjene topline i rada s 

okolinom), težit će uslijed spontanih procesa u sustavu (procesa koji se odvijaju sami od 

sebe), svom ravnotežnom stanju. Ravnotežno stanje sustava se ne može više mijenjati 

samo od sebe. 

Sve makroskopski mjerljive veličine, koje svojim vrijednostima opisuju stanje 

termodinamičkog sustava, nazivaju se veličinama stanja. Takve su veličine npr. tlak p, 

volumen V, temperatura T, unutarnja energija U, entropija S itd. 

Veličine stanja kojima vrijednosti ovise o količini materije unutar termodinamičkog 

sustava se nazivaju ekstenzivnim (npr. V, U, S) a veličine kojima vrijednost ne ovisi o 

količini materije se nazivaju intezivnim veličinama (p i T). Ekstenzivne veličine izražene 

po jedinici mase se nazivaju specifičnim veličinama stanja. Npr. specifični volumen je 

dV1 

definiran izrazom v = = , što je po definiciji jednako recipročnoj vrijednosti gustoće 

dm 

ρ 

fluida. 

Spontani procesi koji dovode termodinamički sustav u ravnotežno stanje, a koji se odvijaju 

sami od sebe, posljedica su postojanja gradijenata fizikalnih veličina (npr. prijelaz topline s 

područja više na područje niže temperature je posljedica postojanja gradijenta temperature, 

miješanje plinova je posljedica postojanja gradijenta koncentracije). Spontani procesi su 

kao što je poznato iz iskustva jednosmjerni procesi (nikad se neće dogoditi da toplina sama


od sebe prijeđe s hladnijeg na toplije područje, a jednom izmiješani plinovi se neće nikad 

sami od sebe razdvojiti). Iz rečenog je jasno da u ravnotežnom stanju, u kojem su iščezli 

svi spontani procesi, nema više gradijenata intenzivnih i specifičnih veličina stanja. 

Jednadžbe stanja – savršeni plin 

Svako ravnotežno stanje termodinamičkog sustava, opisano je skupom veličina stanja, pri 

čemu među veličinama stanja postoje veze, dane jednadžbama stanja, tako da je 

ravnotežno stanje jednoznačno definirano ograničenim brojem veličina stanja. Svaka 

homogena tvar karakterizirana je svojim jednadžbama stanja do kojih se dolazi mjerenjem, 

a u nekim posebnim slučajevima s pomoću statističke mehanike, odnosno kinetičke teorije 

plinova. Tako je npr. za model idealnog plina (koji će se u mehanici fluida zvati savršenim, 

jer je termin idealni rezerviran za neviskozne fluide), ravnotežno stanje određeno s dvije 

veličine stanja, npr. T i v . Tlak je definiran toplinskom (termičkom) jednadžbom stanja 

pv = RT ili p = ρRT 

gdje je R plinska konstanta. Unutarnja energija savršenog plina funkcija je samo 

temperature, što je iskazano kaloričkom jednadžbom stanja 

du = c d T ili u = cT + konst. 

v v 

gdje je c specifični toplinski kapacitet pri konstantnom volumenu. Za specifični toplinski 

v 

kapacitet pri konstantnom tlaku vrijedi cp = cv + R. 

Za savršeni plin su 

κ 

1 

konstante. Uz oznaku κ = cp/ cv 

vrijedi: cp= R i cv= R. 

κ −1 

κ −1 

cp, cv i R 

Termodinamički proces 

Ravnotežno stanje termodinamičkog sustava se može promijeniti samo djelovanjem iz 

okoline, npr. dovođenjem topline ili rada termodinamičkom sustavu, što se naziva 

termodinamičkim procesom. Za termodinamički proces se kaže da je ravnotežan ako 

termodinamički sustav tijekom procesa prolazi samo kroz ravnotežna stanja. To bi značilo 

da se stanje termodinamičkog sustava mijenja samo pod djelovanjem izvana, a prestankom 

tog procesa prestaje se mijenjati i stanje termodinamičkog sustava. Drugim riječima, 

ravnotežni proces ne izaziva spontane procese, što znači da se tijekom ravnotežnog 

procesa u termodinamičkom sustavu ne pojavljuju gradijenti veličina stanja. Iz rečenog je 

jasno da će svaki neravnotežni proces zbog izazvanih spontanih procesa biti jednosmjeran 

ili ireverzibilan. Nužan uvjet da bi se proces mogao odvijati u oba smjera je da je 

ravnotežan. 

Prvi zakon termodinamike (zakon očuvanja energije) 

Zakon očuvanja energije kaže da će promjena ukupne energije termodinamičkog sustava 

između dva stanja (npr. početnog stanja 1 i krajnjeg stanja 2) biti jednaka izmijenjenoj 

toplini i izmijenjenom radu s okolinom između ta dva stanja. Pod ukupnom energijom 

sustava podrazumijeva se suma svih oblika energije koji se tijekom procesa mijenjaju. Ako 

se promatra mirujući plin onda je dovoljno promatrati unutarnju energiju U , a u mehanici 

fluida gdje dolazi do promjene brzine strujanje plina bit će nužno uvesti i kinetičku 

energiju E fluida. Ako je 12 izmijenjena toplina između dva stanja, izmijenjeni rad, 

tada vrijedi 

Q 12 W 

( ) ( ) 

E + U − E + U = Q + W 

2 2 1 1 12 12 

(Napomena: Rad i toplina su definirane kao pozitivne veličine ako se dovode 

termodinamičkom sustavu).


Primjeri primjene prvog zakona termodinamike 

Primjer 1. Jouleov pokus 

Termodinamički sustav se sastoji od toplinski izolirane posude, mirujuće viskozne 

kapljevine i sustava utega, kolotura i lopatica. Uteg svojim spuštanjem za visinu h vrši rad 

W12 = G ⋅ h kojim se putem užeta i kolotura pokreću lopatice i fluid, čime im se povećava 

kinetička energija. Ako se zanemari utjecaj trenja u sustavu kolotura i užeta, sav izvršeni 

rad će se predati lopaticama i fluidu. Uslijed viskoznosti fluida on će se nakon određenog 

vremena spontano zaustaviti i tako ponovo doći u ravnotežno stanje. Ako je posuda bila 

toplinski izolirana, zaključuje se da se sav 

rad utega pretvorio u unutarnju energiju 

fluida, lopatica i posude, što se očituje 

kroz porast njihove temperature. Treba 

primijetiti da je termodinamički sustav 

između početnog i krajnjeg ravnotežnog 

stanja prolazio kroz neravnotežna stanja u 

kojima se fluid gibao, uslijed čega su 

G postojali gradijenti veličina stanja. Zakon 

h 

očuvanja energije primijenjen između 

početnog i krajnjeg ravnotežnog stanja 

mirovanja glasi: 

U − U = W ili u − u = w 

Primjer 2. Stlačivanje plina u toplinski 

izoliranom cilindru 

Termodinamički sustav sadrži plin, koji se nalazi u toplinski izoliranom cilindru s 

pomičnim stapom. Pretpostavlja se da plin u početnom trenutku miruje, te da ga se polako 

stlačuje putem stapa, kojeg se pomiče bez trenja, silom F koja je u svakom trenutku u 

ravnoteži sa silom tlaka unutar cilindra, dakle, F=pA (pretpostavlja se da je vanjski tlak 

2 1 jednak nuli). Budući je suma sila na stap jednaka nuli, on 

se po prvom Newtonovom zakonu može gibati jedino 

A 

pA 

F 

konstantnom brzinom. Neka se stap giba beskonačno 

malom brzinom, tako da se kinetička energija čestica 

plina u cilindru može zanemariti. Budući da nema 

izmjene topline, sav rad koji se ulaže putem sile F = pA 

s 

troši se na promjenu unutarnje energije plina, tj. vrijedi: 

V v 

2 2 

∫ ∫ 

U− U=− pV d ili u− u=− pv d 

2 1 2 1 

V1 v1 

s 

2 

1 

W12 = Fds = pA �ds 

=− pdV 

12 

2 s2 V2 

∫ ∫ ∫ 

S1 

V 

s −d 

1 V1 

Primjer 3. Grijanje plina pri konstantnom volumenu 

Termodinamički sustav sastoji se od zadane količine plina, početne temperature T0, 

smještene u krutu posudu zadanog volumena, kroz čiju se stijenku plinu dovodi toplina od 

ogrjevnog spremnika temperature T1. Budući da je posuda stalnog volumena, pri grijanju 

plina ne dolazi do pomicanja stijenki posude prema okolini što znači da plin ne vrši 

2 

1 

12

h 

V=konst. 

T0 

ogrjevni spremnik, T1 

A 

G 

p=G/A=konst. 


2 

1 

nikakav rad, pa sva dovedena toplina Q12 prelazi u 

unutarnju energiju termodinamičkog sustava, tj. vrijedi 

U 2 − U1 

= Q12 

ili u 2 − u1 

= q12 

Specifični toplinski kapacitet je toplina koju treba dovesti 

jedinici mase tvari da bi joj se temperatura povisila za 1 

K. Specifični toplinski kapacitet cv pri konstantnom 

⎛ dq ⎞ ⎛ du 

⎞ 

volumenu se definira kao cv 

= ⎜ ⎟ = ⎜ ⎟ 

⎝dT ⎠ ⎝dT ⎠ . 

v= konst. 

v 

Primjer 4. Grijanje plina pri konstantnom tlaku 

Termodinamički sustav sadrži plin konstantne početne 

temperature, koji je zatvoren u cilindru s pomoću 

pomičnog stapa (koji idealno brtvi, a pomiče se bez 

trenja), čija je površina A, a težina zajedno s utegom G, 

tako da je konstantni tlak u plinu p=G/A (pretpostavlja 

se da je vanjski tlak jednak nuli). Dovođenjem topline 

termodinamičkom sustavu mijenja se volumen plina te 

dolazi do pomicanja stapa s utegom prema gore, što 

znači da termodinamički sustav vrši mehanički rad, koji 

je jednak umnošku težine G i visine h pomaka stapa. 

Ako se težina G izrazi s pomoću tlaka plina G=pA, tada 

izraz za izvršeni rad termodinamičkog sustava glasi: 

W =− pAh=−p V − V 

ogrjevni spremnik, T1 ( ) 

12 2 1 

gdje su V1 i V2 volumeni plina u početnom i krajnjem 

ravnotežnom stanju. Prema tome ako je Q12 toplina dovedena između početnog i krajnjeg 

stanja, prvi zakon termodinamike poprima oblik 

U − U = Q − p V −V ili u − u = q − p v − v 

( ) ( ) 

2 1 12 2 1 2 1 12 2 1 

Treba ponovo naglasiti, da će termodinamički sustav pri prijelazu iz stanja 1 u stanje 2 

prolaziti kroz niz ravnotežnih stanja samo ako se dovođenje topline odvija vrlo sporo. U 

tom se slučaju prvi zakon termodinamike može postaviti za dva vrlo bliska stanja između 

kojih je dovedena diferencijalno mala količina topline dq, izvršen je infinitezimalno mali 

rad dw=-pdv, pa je i promjena unutarnje energije du infinitezimalno mala. Time se dolazi 

do diferencijalnog oblika prvog zakona termodinamike, koji glasi 

du = dq 

− pdv 

Treba još jednom naglasiti da gornji oblici prvog zakona termodinamike vrijede samo za 

ravnotežne promjene stanja. Kod brzog dovođenja topline, u plinu bi se pojavio gradijent 

temperature, gibanje plina i gradijent tlaka, te za stap više ne bi vrijedila mehanička 

ravnoteža (G=pA), jer bi se on mogao gibati ubrzano, te postići konačnu brzinu. U tom 

slučaju ne bi vrijedio izraz za izvršeni rad pa zbog toga ni dani izraz za prvi zakon 

termodinamike. 

Entalpija 

Iz diferencijalne formulacije prvog zakona termodinamike du = dq 

− pdv 

, jasno je da za 

v=konst. sva dovedene toplina prelazi u unutarnju energiju, pa slijedi jednostavni izraz za 

specifični toplinski kapacitet cv. Za procese pri konstantnom tlaku zgodno je uvesti 

entalpiju h u obliku d h = 

dq 

+ vdp 

. Držeći p=konst. (dp=0) jasno je da se sva dovedena


toplina pretvara u entalpiju, pa se dobije jednostavna definicija specifičnog toplinskog 

⎛ dq 

⎞ ⎛ dh 

⎞ 

kapaciteta cp 

pri konstantnom tlaku cp = ⎜ = ⎜ ⎟ 

T 

⎟ 

. 

⎝ d ⎠ ⎝ dT 

p ⎠ p 

Veza između entalpije i unutarnje energije se dobije ako se desnoj strani izraza kojim je 

definirana entalpija doda i oduzme član pdv, te slijedi izraz 

, a nakon integracije slijedi 

( ) �� 

d h = dq 

− pdv 

+ pdv 

+ vdp 

du 

d pv 

h = u + pv ili H = U + pV 

U gornjim relacijama entalpija je izražena samo veličinama stanja pa je ona također 

veličina stanja. 

Povratni, nepovratni procesi i entropija 

Ako se sustav određenim procesom dovede iz jednog u drugo ravnotežno stanje i ako bi se 

sustav mogao vratiti u početno ravnotežno stanje bez da u okolini ostane trajnih i 

zamjetljivih promjena, proces je povratan ili reverzibilan. 

Svi prirodni ili spontani procesi posljedica su postojanja gradijenata fizikalnih veličina u 

termodinamičkom sustavu i nepovratni su ili ireverzibilni. Prema tome, nužan uvjet da bi 

proces bio reverzibilan je da je ravnotežan. 

Primjer reverzibilnog procesa je polagana kompresija plina bez trenja u toplinski 

izoliranom cilindru, kao što je opisano u primjeru 2. Iz tog je primjera vidljivo da u 

adijabatskom procesu bez trenja i pri polaganoj kompresiji (koja se odvija pri mehaničkoj 

ravnoteži) unutarnja energija predstavlja potencijal za silu tlaka (odnosno tlak) jer se 

uloženi mehanički rad kompresije može putem polagane ekspanzije u potpunosti povratiti. 

Iz prvog zakona termodinamike za taj slučaj očito je da vrijedi: 

du 

p =− 

dv 

bez izmjene topline, bez trenja i u ravnotežnom procesu 

gdje se gornja derivacija odnosi na slučaj ravnotežnog procesa bez trenja i bez izmjene 

topline. Da ne bismo morali opisno davati uz koje uvjete vrijedi gornja jednadžba, uvodi se 

nova veličina stanja, entropija s, koja pod danim uvjetima ostaje konstantna. U općem 

slučaju unutarnja energija je funkcija dviju veličina stanja, te se gornja jednadžba piše 

u 

p 

v ⎟ 

s 

⎟ 

⎛ ∂ ⎞ 

= − ⎜ 

⎝ ∂ ⎠ 

Uvođenjem entropije u gornjem izrazu nije još definirana njena veličina. Jedino je očito da 

će do promjene entropije s doći kada dođe do izmjene topline, trenja ili neravnoteže. Ako 

se dogovori da za slučaj dovođenja topline pri stalnom volumenu kao u primjeru 3 (gdje 

rastu unutarnja energija i temperatura plina) entropija s raste, tada se veličina promjene 

entropije s definira iz relacije 

u 

T 

s 

⎟ 

v 

⎟ 

⎛ ∂ ⎞ 

= ⎜ 

⎝ ∂ ⎠ 

S obzirom da je apsolutna temperatura T pozitivna veličina, svako povećanje unutarnje 

energije (dovođenje topline) pri konstantnom volumenu ima za posljedicu povećanje 

entropije, a odvođenje topline smanjenje entropije. 

Ako se unutarnja energija prikaže kao funkcija entropije i volumena, tada vrijedi


⎛∂u⎞ ⎛∂u⎞ du = ⎜ ⎟ ds+ 

⎜ ⎟ dv , odnosno 

⎝ ∂s ⎠v ⎝ ∂v 

⎠s 

�� 

T − p 

du = T ds 

− pdv 

ili dU = T dS 

− pdV 

usporedbom gornjeg izraza (Gibbsova relacija) s izrazom za prvi zakon termodinamike 

du = dq 

− pdv 

slijedi 

d q = T ds 

ili d Q = T dS 

Treba naglasiti da je gornji izraz izveden pod pretpostavkom neprekidne toplinske i 

mehaničke ravnoteže termodinamičkog sustava što znači da je valjan samo za ravnotežne 

procese. 

Drugi zakon termodinamike 

(a) Ako se stanje termodinamičkog sustava mijenja od stanja 1 do stanja 2 ravnotežnim 

procesom, promjena entropije definirana je integralom 

2 

2 

dq 

dQ 

s 2−s 

1 = ∫ ili S 2−S1 

= 

T 

∫ T 

1 

1 

(b) Svaki spontani proces (koji je po definiciji neravnotežan) u izoliranom zatvorenom 

termodinamičkom sustavu vodi povećanju entropije S. Sustav dolazi u ravnotežno 

stanje kada entropija S postigne svoj maksimum. Prema tome, kod neravnotežnih 

procesa dolazi do povećanja entropije termodinamičkog sustava i kad nema izmjene 

topline, te se prethodni izraz može poopćiti tako da vrijedi za bilo koji proces, tj. za 

promjenu entropije termodinamičkog sustava vrijedi 

2 

2 

dq 

dQ 

s 2−s 

1 ≥ ∫ ili S 2−S1 

≥ 

T 

∫ T 

1 

1 

gdje se znak jednakosti odnosi na ravnotežne procese, a znak veće na neravnotežne, a 

samim tim na ireverzibilne procese. Temeljem prethodnog izraza može se definirati i 

produkcija entropije 

2 

2 

⎛ dq ⎞ 

⎛ dQ 

⎞ 

σ = ∫⎜ ds 

− ⎟ ≥ 0 ili ∑ = ⎜d 

⎟ ≥ 0 

1 ⎝ T 

∫ S − 

⎠ 

1 ⎝ T ⎠ 

gdje se ponovo znak jednakosti odnosi na ravnotežne procese. U izoliranom 

termodinamičkom sustavu produkcija entropije jednaka je promjeni entropije. Ako u 

izoliranom termodinamičkom sustavu nema promjene entropije proces je reverzibilan, a 

ako postoji porast entropije proces je ireverzibilan. Treba naglasiti da u termodinamičkom 

sustavu koji izmjenjuje toplinu s okolinom entropija može rasti (ako mu se toplina dovodi ) 

ili padati (kada mu se toplina odvodi). S druge strane produkcija entropije, koja je mjera 

nepovratnosti termodinamičkog procesa, mora biti jednaka nuli (za ravnotežne procese) ili 

pozitivna veličina (za ireverzibilne procese). 

Termodinamički koncept i strujanje fluida 

Postavlja se pitanje kako gore izloženi koncept iz termodinamike koji je definiran i 

primjenjiv na ravnotežna stanja termodinamičkog sustava, primijeniti u strujanju fluida u 

kojem se tipično pojavljuju gradijenti brzine, tlaka i temperature, koje je dakle 

neravnotežno. Odgovor leži u principu lokalne ravnoteže u kojem se svaka čestica fluida 

(iz koncepta kontinuuma) smatra termodinamičkim sustavom. Budući da čestica fluida 

mase dm zauzima infinitezimalni volumen dV (pri čemu je dm=ρdV), sve ekstenzivne


veličine stanja unutar čestice fluida će također biti infinitezimalne: dU=ρudV, dS=ρsdV, a 

intenzivne i specifične veličine stanja će unutar čestice fluida biti konstantne, što prema 

izloženom konceptu odgovara ravnotežnim uvjetima, pa sve prije spomenute relacije 

vrijede i za svaku česticu fluida. Prema hipotezi kontinuuma, svaka čestica fluida zauzima 

samo jednu točku prostora, pa se u svakoj točki prostora definiraju veličine stanja one 

čestice fluida koja se u promatranom trenutku upravo nalazi u promatranoj točki prostora. 

Na taj će način intenzivne i specifične veličine stanja čestica fluida biti opisane poljima 

fizikalnih veličina koja su funkcija prostornih i vremenske koordinate. S obzirom da svaka 

čestica fluida ostaje cijelo vrijeme u ravnotežnom stanju, znači da toplinska jednadžba 

stanja vrijedi u svakoj točki prostora u svakom vremenskom trenutku. Također vrijedi i 

Gibbsova relacija du = T ds 

− pdv 

, gdje se diferencijali specifične unutarnje energije, 

specifične entropije i volumena odnose na česticu fluida, koja je elementarni 

termodinamički sustav. Dijeljenjem gornjeg izraza s diferencijalom vremena dt dobiju se 

vremenske promjene specifične unutarnje energije, specifične entropije i specifičnog 

volumena čestice fluida, koje se izražavaju materijalnom derivacijom, te Gibbsova relacija 

glasi: 

Du Ds Dv Ds p Dρ 

= T − p = T + 2 

Dt Dt Dt 

Dt ρ Dt 

Slično bi se i dijeljenjem diferencijalnog oblika prvog zakona termodinamike danog 

izrazom (u kojem se uzima u obzir i kinetička energija fluida, a promjena potencijalne 

energije uzima kroz mehanički rad) s diferencijalom vremena dobilo 

D( 

e + u) 

dq 

dw 

= + 

Dt 

dt 

dt 

što bi se moglo iskazati riječima da je brzina promjene kinetičke i unutarnje energije 

čestice fluida jednaka brzini dovođenja topline (dq/dt) i mehaničkog rada (dw/dt) (odnosno 

snazi vanjskih sila na česticu fluida). 

Čestica fluida je u materijalnom volumenu okružena česticama koje su različitih 

temperatura od promatrane čestice, te dolazi do prijelaza topline od ili prema promatranoj 

čestici. S druge strane čestice se dodiruju, što ima za posljedicu pojavu površinskih sila, 

putem kojih promatrana čestice prima ili vrši rad. 

U mehanici fluida će se zakon očuvanja energije primjenjivati i na materijalni volumen, 

koji se sastoji od velikog broja čestica fluida. Zakon očuvanja energije za materijalni 

volumen dobije se zbrajanjem jednadžbi očuvanja energije svih čestice fluida koje čine taj 

materijalni volumen. Budući da su kinetička i unutarnja energija ekstenzivne veličine 

brzina promjene tih energija materijalnog volumena bit će jednaka zbroju brzina promjena 

tih energija svih čestica fluida unutar materijalnog volumena. Zbroj brzina izmjene topline 

svih čestica fluida unutar materijalnog volumena, bit će jednak brzini izmjene topline 

materijalnog volumena s okolinom, jer će se izmjena topline među česticama unutar 

materijalnog volumena međusobno poništiti. Isto vrijedi i za snagu površinskih sila. Ako 

dvije čestice u unutrašnjosti materijalnog volumena izmjenjuju energiju putem snage 

površinskih sila, onda je zbroj tih snaga jednak nuli, a u materijalnom volumenu ostaje 

samo snaga površinskih sila koja se izmjenjuje s okolinom na granici materijalnog 

volumena. Snaga masenih sila koje djeluju na materijalni volumen, jednaka je zbroju snaga 

koje djeluju na čestice fluida. Dakle, iskazano riječima, zakon održanja energije za 

materijalni volumen glasi: Brzina promjena kinetičke i unutarnje energije materijalnog 

volumena jednaka je snazi vanjskih masenih i površinskih sila koje djeluju na materijalni 

volumen i brzini izmjene topline materijalnog volumena s okolinom.


OSNOVNE JEDNADŽBE DINAMIKE FLUIDA 

Zakon očuvanja mase (jednadžba kontinuiteta) 

Zakon očuvanja mase, za materijalni volumen, glasi: Brzina promjene mase 

materijalnog volumena jednaka je nuli. Matematički zapis ovog zakona je 

D 

ρ dV 

= 0 

Dt 

∫ 

VM 

( t) 

Diferencijal dV vremenski promjenjivog materijalnog volumena M () 

V t , koji odgovara 

volumenu čestice fluida, je također vremenski promjenjiv, pri čemu vrijedi (vidjeti npr. 

sažetak drugih predavanja) 

1 Dd ( V ) ∂v 

j 

= 

dV Dt 

∂xj 

pa je 

⎛ ⎞ ⎛ ⎞ 

⎜ ⎟ ⎜ ⎟ 

D ⎜Dρ Dd ( V ) ⎟ ⎜ Dρ 

∂v 

j ⎟ 

dV dV dV 0 

Dt ∫ ρ = ∫ ⎜ + ρ ⎟= Dt Dt ∫ ⎜ + ρ 

M() M() M() 

�Dt 

x 

⎟ = 

V t V t ⎜ �� ⎟ ∂ 

V t 

j 

⎜ ⎟ 

∂v 

∂ρ ∂ρ 

⎜ j 

⎜ dV 

⎟ ⎜ + v j ⎟ 

∂x 

∂t ∂x 

j ⎝ j 

⎝ ⎠ 

⎠ 

U graničnom prijelazu kada se materijalni volumen smanji na česticu fluida (materijalnu 

⎛Dρ∂v⎞ j 

točku), gornji izraz prelazi u oblik ⎜ + ρ ⎟dVM= 

0, 

iz čega je jasno da vrijedi 

⎜ Dt 

∂x 

⎟ 

⎝ j ⎠ 

Dρ 

∂vj ∂ρ ∂ρ 

∂vj 

+ ρ = + v j + ρ = 0 . 

Dt 

∂xj ∂t ∂xj ∂xj 

Gornji izraz se može zapisati i u obliku 

∂ρ 

∂( 

ρ v j ) 

+ = 0 

∂t 

∂x 

j 

koji se naziva konzervativnim oblikom zakona očuvanja mase (jednadžbe kontinuiteta). Za 

nestlačivo strujanje (stacionarno ili nestacionarno) jednadžba kontinuiteta glasi: 

∂v 

j 

= 0 

∂x 

j 

a izražava činjenicu da nema promjene volumena čestice fluida. 

Dva pomoćna pravila u izvodu osnovnih zakona dinamike fluida 

Bilo koje fizikalno svojstvo fluida (masa, količina gibanja, energija, …) moguće je izraziti 

volumenskom gustoćom Φ ili masenom gustoćom ϕ (fizikalna veličina izražena po 

jedinici mase je specifična vrijednost fizikalne veličine). Tako je npr. volumenska gustoća 

mase m jednaka Φ=d m/ dV 

= ρ , specifična masa ϕ =d m/ dm= 1. 

Za kinetičku energiju 

v 

Veza između volumenske gustoće i specifične fizikalne veličine je 

Φ = 

ρϕ 

2 2 

2 

mv /2 je volumenska gustoća Φ= ρ /2, 

a specifična kinetička energija je ϕ = /2. 

v


U svim zakonima dinamike fluida pojavljuje se pojam brzine promjene sadržaja fizikalnog 

svojstva unutar materijalnog volumena. Brzina promjene izražava se materijalnom 

derivacijom, a sadržaj fizikalne veličine integralom po materijalnom volumenu. Taj se 

sadržaj može izraziti ili s pomoću volumenske gustoće Φ ili s pomoću masene gustoće ϕ 

fizikalnog svojstva, u obliku ΦdV = ρϕdV 

∫ ∫ , pa za brzinu promjene sadržaja vrijedi 

VM() t VM() t 

D D D DϕDϕ ΦdV � 

dV dm dm dV 

Dt ∫ = 

Dt ∫ ϕρ = 

Dt ∫ϕ= ∫ = 

Dt ∫ ρ 

Dt 

VM() t VM() t dm 

m m VM() t 

U gornjim je izrazima iskorištena činjenica da je masa m materijalnog volumena 

konstantna (kao i masa dm čestice fluida), pa se u tom slučaju pri uvođenju operatora 

materijalne derivacije, operator primjenjuje samo na podintegralnu funkciju. Dakle valja 

zapamtiti pravilo (nazovimo ga pravilom A) 

D Dϕ 

dV dV 

Dt ∫ ρϕ = ∫ ρ pravilo A 

Dt 

VM() t VM() t 

Podintegralna funkcija u gornjem izrazu nakon razvoja operatora materijalne derivacije je 

Dϕ 

⎛ ∂ϕ ∂ϕ 

⎞ 

ρ = ρ⎜ + v j 

Dt 

⎜ 

⎟ 

t x ⎟ 

⎝ ∂ ∂ j ⎠ 

Ako se desnoj strani gornjeg izraza doda jednadžba kontinuiteta pomnožena s ϕ slijedi 

⎛ ⎞ 

Dϕ 

∂ϕ ∂ϕ ⎜ 

∂ρ 

∂( 

ρv 

j ) ⎟ 

ρ = ρ + ρvj+ ϕ⎜ 

+ ⎟ 

Dt 

∂t ∂x ⎜ ∂t ∂x 

⎟ 

�� 

j j 

⎜ ⎟ 

⎝ = 0 prema jednadžbi kontinuiteta ⎠ 

dobije se: 

Dϕ 

∂ϕ ρ = ρ + ρvj 

Dt 

∂t ∂ϕ 

= 

∂xj ∂( 

ρϕ ) ∂( 

ρv jϕ 

) 

+ 

∂t ∂xj 

pravilo B 

Valja zapamtiti ovo jednostavno pravilo koje će poslužiti za definiranje konzervativnih 

oblika osnovnih zakona (treći oblik u pravilu B). 

Zakon očuvanja količine gibanja (jednadžba gibanja fluida) 

Zakon količine gibanja za materijalni volumen glasi: Brzina promjene količine gibanja 

materijalnog volumena jednaka je sumi vanjskih masenih i površinskih sila koje 

djeluju na materijalni volumen. Matematički zapis, riječima iskazanog zakona količine 

gibanja je (pogledati i sažetak 8. predavanja iz MFI): 

D 

vidV fidV �i 

dS fidV nj jidS 

Dt 

∫ ρ = ∫ ρ + ∫ σ = ∫ ρ + ∫ σ 

VM() t VM() t SM() t n 

VM() t SM() t 

jσji Primjenom pravila A na lijevu stranu gornjeg izraza i prikazom površinskih sila preko 

volumenskog integrala, slijedi: 

Dv ∂σ 

i 

ji 

∫ ρ dV = fidV dV 

Dt 

∫ ρ + ∫ ∂x 

VM() t VM() t VM() t j 

Iz gornjeg izraza slijedi nekonzervativni diferencijalni zapis zakona količine gibanja koji 

glasi:

1 


Dv 

∂σ 

i 

ji 

ρ = ρ fi 

+ 

Dt 

∂xj 

Množenjem gornjeg izraza s volumenom čestice fluida, dobije se poznati oblik drugog 

Newtonovog zakona za gibanje čestice fluida, u kojem je lijeva strana jednadžbe jednaka 

umnošku mase čestice fluida i njena ubrzanja (materijalna derivacija brzine), a desna 

strana je jednaka zbroju sila koje djeluju na česticu fluida, ovdje su to masena i površinska 

sila. 

Primjenom pravila B na lijevu stranu gore dane jednadžbe količine gibanja 

Dv 

∂σ 

i 

ji 

ρ = ρ fi 

+ slijedi konzervativni diferencijalni zapis zakona količine gibanja, 

Dt 

∂xj 

koji glasi: 

∂( 

ρv 

) ∂ i ( ρvv j i) ∂σ 

ji 

+ = ρ fi 

+ , a prema pravilu B jasno je da vrijedi i 

∂t ∂xj ∂xj 

∂vi ∂v 

∂σ 

i 

ji 

ρ + ρvj = ρ fi 

+ , 


što je nekonzervativni oblik jednadžbe količine gibanja. 

Volumenska gustoća ukupne površinske sile na česticu fluida je matematički definirana 

∂σ 

ji 

divergencijom tenzora naprezanja , što naravno označuje vektor. Komponente toga 

∂x 

j 

vektora dobiju se razvojem izraza za i = 1, 

2 i 3, npr. komponenta površinske sile u smjeru 

osi x 1 (za i = 1) 

je 

∂σ j1 

∂σ11∂σ21 ∂σ31 

= + + 

∂xj∂x1 ∂x2 ∂x3 

Fizikalna interpretacija gornja tri člana slijedi iz analize površinskih sila na česticu fluida 

oblika elementarnog paralelopipeda sa stranicama dx 1, 

dx 2 i dx 3 , kao što prikazuje slika. 

Na prikazanu česticu fluida ucrtane su 

x3 

samo sile u smjeru osi x 1 , a na svim 

∂σ31 

σ 

σ 

površinama su pretpostavljene pozitivne 

31 + dx3 

11 

∂x3 

komponente tenzora naprezanja. Težišta 

3' 

∂σ 

površina u kojima djeluju površinske sile 

21 

σ 

σ21 

+ dx2 

21 

1 

∂x 

su označena brojevima 1 do 3 i 1' do 3'. 

2 

2 

2' 

Površine 1 do 3 imaju normale u 

1' 

negativnim smjerovima osi, pa na njima 

x2 

3 

pozitivna naprezanja gledaju u 

negativnom smjeru osi x 1 (vidjeti 

x1 

∂σ 

σ 

11 

31 

σ11 

+ dx1 

∂x 

0 dogovor o predznacima naprezanja u 

1 

sažetku 2. predavanja iz MF I). 

Normale površina 1' do 3' su u pozitivnim smjerovima osi, pa pozitivna naprezanja na tim 

površinama gledaju u pozitivnom smjeru osi x 1 . Komponente naprezanja su u općem 

slučaju funkcije prostornih koordinata. Ako na površini 1 (u težištu 1) vlada naprezanje 

σ 11, 

onda će u bliskoj točki 1', koja je od točke 1 pomaknuta u smjeru osi x 1 , doći do 

∂σ11 

∂σ11 

prirasta naprezanja dx1 

tako da je u težištu 1' naprezanje σ11 

+ dx1 

. Slično vrijedi 

∂x 

∂x 

1


i za priraste naprezanja σ 21 i σ 31 . Elementarna sila u smjeru osi x 1 na površini 1 je 

⎛ σ ⎞ 

11 

− σ11dx2dx3, 

a na površini 1' ⎜ ∂ 

⎜σ11 + dx ⎟ 1 dx2dx3 x 

⎟ . Doprinos površinskoj sili u smjeru osi 

⎝ ⎜ ∂ ⎟ 

1 ⎠ 

⎛ σ ⎞ 

21 

x 1 na površini 2 je − σ21dx1dx3, 

a na površini 2' ⎜ ∂ 

⎜σ21 + dx ⎟ 2 dx1dx3 x 

⎟ . Analogno vrijedi i 

⎜ ⎜⎝ ∂ ⎟ 

2 ⎠ 

za površine 3 i 3'. Ukupna površinska sila na česticu fluida jednaka je zbroju sila na šest 

površina i iznosi 

⎛ σ11σ21 σ ⎞ 

⎜∂ ∂ ∂ 31⎟ 

∂σ 

j1 

∂σ 

j1 

⎜ ⎟ 

⎜ 

+ + dx1dx2dx3= dV 

⎜ ∂x1 ∂x2 ∂x ⎟ 

, pa je jasno da je volumenska 

⎝ ⎟ 

3 ⎠ 

∂xj 

∂x 

j 

gustoća površinske sile na česticu fluida u smjeru osi x 1 . 

Zakon očuvanja momenta količine gibanja 

Zakon momenta količine gibanja za materijalni volumen glasi: Brzina promjene 

momenta količine gibanja materijalnog volumena, u odnosu na odabrani pol, jednaka 

je sumi momenata vanjskih masenih i površinskih sila koje djeluju na materijalni 

volumen, u odnosu na taj isti odabrani pol. Ako se pretpostavi da u fluidu nema 

momenata (spregova sila) raspodijeljenih po površini materijalnog volumena ili unutar 

samog volumena, tada se zakon očuvanja momenta količine gibanja svodi na činjenicu 

simetričnosti tenzora naprezanja σ jk = σ kj (vidjeti sažetak 12. predavanja iz MFI). Ako se 

unaprijed pretpostavi simetričnost tenzora naprezanja, to znači da je jednadžba momenta 

količine gibanja već zadovoljena (može se tvrditi da je već iskorištena pri definiranju 

tenzora naprezanja), pa se tu jednadžbu više ne treba uključivati u skup osnovnih jednadžbi 

dinamike fluida. 

Zakon očuvanja energije 

Zakon očuvanja energije za materijalni volumen glasi: Brzina promjene zbroja kinetičke 

i unutarnje energije materijalnog volumena jednaka je snazi vanjskih masenih i 

površinskih sila koje djeluju na materijalni volumen, te brzini izmjene topline 

materijalnog volumena s okolinom. 

x1 

f i 

x3 

O 

q j 

n j 

SM 

x2 

dS 

idS σ 

dm=ρdV 

VM 

ρ fidV v 

i 

Ako se sa u označi specifična 

unutarnja energija čestice fluida, tada 

je zbroj kinetičke i unutarnje energije 

unutar čestice fluida mase dm= ρdV 

jednak 

2 2 

v ⎛v ⎞ 

ρdV + ρdVu = ρ⎜ + u⎟dV . 

2 ⎝ 2 ⎠ 

Energija materijalnog volumena 

jednaka je zbroju (integralu) energija 

svih čestica unutar materijalnog 

volumena, a brzina promjene te 

energije označuje se materijalnom 

derivacijom toga integrala, tj. vrijedi

Brzina promjene energije V M = 


2 

D ⎛v ⎞ D De 

u dV edV dV 

Dt ∫ ρ⎜ + ⎟ = ρ = ρ 

2 Dt ∫ ∫ , 

⎝ ⎠ 

Dt 

�� 

VM() t VM() t VM() t 

e 

Gdje je za zbroj specifične kinetičke i unutarnje energije uvedena oznaka e , i primijenjeno 

pravilo A, za materijalnu derivaciju integrala po vremenski promjenjivom materijalnom 

volumenu. 

Snaga masenih sila na česticu fluida izražava se skalarnim produktom masene sile na 

česticu fluida fi ρ dV i njene brzine vi, a ukupna snaga masenih sila u materijalnom 

volumenu jednaka je zbroju, odnosno integralu tih elementarnih snaga unutar materijalnog 

volumena, tj. vrijedi 

Snaga masenih sila u materijalnom volumenu = fiv 

i V d ∫ ρ 

V ( t) 

Vanjske površinske sile djeluju po materijalnoj površini SM(t), a definirane su vektorom 

naprezanja σ i , koji je jednak skalarnom umnošku jediničnog vektora normale n j na 

materijalnu površinu i tenzora naprezanja σ ji u točki materijalne površine σ i = n jσji. Na 

svaki elementarni dio dS materijalne površine djeluje elementarna površinska sila σ idS , a 

snaga te elementarne sile se dobije njenim skalarnim množenjem s vektorom brzine v i 

pomicanja materijalne površine (koja je jednaka brzini strujanja fluida). Ukupna snaga 

površinskih sila koje djeluju na materijalni volumen dobije se zbrajanjem, odnosno 

integriranjem tih elementarnih snaga po čitavoj materijalnoj površini, tj. vrijedi: 

M 

∂( 

σ jivi ) 

∫ σivdS i = ∫ njσ jivdS i = ∫ dV, 

Snaga površinskih sila na V M = 

∂x 

SM() t SM() t VM() t j 

gdje je iskorištena Gaussove formula da se ukupna snaga površinskih sila na materijalni 

∂( 

σ jivi ) 

volumen, prikaže volumenskim integralom. Tako bi član imao fizikalno značenje 

∂x 

j 

volumenske gustoće snage površinskih sila na česticu fluida. 

Treći uzrok promjeni energije materijalnog volumena je izmjena topline kroz materijalnu 

površinu. Ako se sa q i označi vektor površinske gustoće toplinskog toka (jedinica u SI 

2 

sustavu mjera je W/m ), onda je toplinski tok (izmijenjena toplina u jedinici vremena) 

kroz elementarni dio materijalne površine razmjeran normalnoj komponenti tog vektora 

(vektor i q skalarno pomnožen s jediničnim vektorom n i vanjske normale na materijalnu 

površinu) i elementarnoj površini dS . Ukupna snaga toplinskog toka jednaka je integralu 

tih elementarnih tokova kroz cijelu materijalnu površinu: 

∂qi 

Toplinski toka kroz materijalnu površinu = − ∫ qndS i i =− ∫ dV 

∂x 

SM() t VM() t i 

Toplinski tok se uzima s negativnim predznakom jer pozitivna normalna komponenta 

vektora površinske gustoće toplinskog toka qn i i označuje odvođenje topline iz 

materijalnog volumena što znači smanjenje ukupne energije materijalnog volumena. Jasno 

je da se površinski integral može primjenom Gaussove formule prevesti na volumenski 

∂qi 

integral, u kojem divergencija vektora površinske gustoće toplinskog toka 

∂ xi 

označuje 

volumensku gustoću brzine izmjene topline čestice fluida s okolinom. 

Matematički zapis riječima iskazanog zakona očuvanja energije je dakle


( σ v ) 

∫ ρ = ∫ ρ i i + ∫ − ∫ 

De ∂ ji i ∂qi 

dV fvdV dV dV 

Dt 

∂x VM() t VM() t VM() t j ∂x 

VM() t i 

Sažimanjem materijalnog volumena na česticu fluida i dijeljenjem gornjeg izraza s 

volumenom čestice fluida dobije se diferencijalni oblik zakon očuvanja energije 

De 

∂( σ jivi ) ∂qi 

ρ = ρ fv i i+ 

− 

Dt 

∂xj ∂ xi 

Primjenom pravila B na lijevu stranu gornjeg izraza dobije se 

∂e ∂e ∂( 

σ jivi ) ∂qi 

ρ + ρvj = ρ fv i i + − 

∂t ∂x ∂x ∂ x 

i 

j j i 

( ρ ) ∂( ρve) ∂( 

σ v) 

∂ e j ji i ∂qi 

+ = ρ fv i i+ 

− 

∂t ∂xj ∂xj ∂xi 

gdje je ovaj posljednji oblik konzervativni zapis zakona očuvanja energije. 

U gornjoj jednadžbi drugi član desne strane označuje volumensku gustoću snage 

površinskih sila, a može se deriviranjem produkta razložiti na dva dijela: 

( ) 

∂ σ jivi ∂σ ji ∂v 

∂σ 

i 

ji 

= vi+ σ ji = vi+ σ ji Dji 

∂x � � 

j ∂xj ∂xj ∂xj 

� � naprezanje tenzor 

Dji + Vji 

rezultirajuća na površini brzine 

površinska čestice deformacije 

�� 

sila 

�� snaga površinskih sila 

ubrzava česticu koja se troši na 

fluida ⇒ mijenja deformaciju čestice 

kinetičku energiju fluida ⇒ mijenja 

unutarnju energiju 

Iz diferencijalnog oblika jednadžbe količine gibanja je poznato da divergencija tenzorskog 

polja naprezanja ji / j x σ ∂ ∂ označuje rezultantnu površinsku silu na česticu fluida izraženo 

po jedinici volumena, te će umnožak tog člana s brzinom čestice fluida označavati 

volumensku gustoću snage površinske sile kojom se mijenja kinetičku energiju čestice 

fluida, sukladno zakonu kinetičke energije u mehanici. U drugom članu gornje jednadžbe 

se pojavljuje tenzor gradijenta brzine ∂vi/ ∂ xj, 

koji se, kao što je poznato iz kinematike, 

može prikazati zbrojem tenzora brzine deformacije i tenzora vrtložnosti. Tenzor vrtložnosti 

je antisimetričan tenzor, te je njegov dvostruki skalarni produkt sa simetričnim tenzorom 

naprezanja jednak nuli, tako da je drugi član produkt tenzora naprezanja (površinske sile) i 

tenzora brzine deformacije, iz čega se zaključuje da on označuje dio snage površinskih sila 

kojom se deformira čestica fluida, a snaga te deformacije se pretvara u unutarnju energiju, 

kao što je poznato iz termodinamike. 

Drugi zakon termodinamike 

Drugi zakon termodinamike spada u skup osnovnih zakona, a ukazuje na jednosmjernost 

odvijanja realnih termodinamičkih procesa. Ovaj je zakon izražen činjenicom da entropija 

izoliranog sustava mora rasti ili u najboljem slučaju ostati ista, odnosno da produkcija 

entropije u otvorenom termodinamičkom sustavu mora biti pozitivna ili jednaka nuli. 

Glavna primjena ovog zakona u dinamici fluida je za ocjenu valjanosti (fizikalnosti) 

dobivenih rješenja strujanja fluida. Ukoliko postoji više rješenja nekog problema strujanja,


uzima se ono koje je u skladu s drugim zakonom termodinamike. Brzina promjene 

entropije čestice fluida definirana je Gibbsovom jednadžbom danom u prethodnom 

predavanju, a koja glasi 

Du Ds 

1 Dρ 

ρ = ρT 

+ p 

Dt 

Dt ρ Dt 

Primjenom jednadžbe kontinuiteta 1Dρ 

∂v 

j 

=− na zadnji član desne strane gornjeg 

ρ Dt 

∂xj 

izraza, slijedi: 

Ds 

Du 

∂v 

j 

ρ T = ρ + p 

Dt Dt 

∂x 

j 

S obzirom da se entropija ne pojavljuje u ostalim osnovnim zakonima dinamike fluida, 

gornja se jednadžba može rješavati nezavisno od ostalih jednadžbi, pa se ona naziva i 

“pasivnom” jednadžbom, što znači da se drugi zakon termodinamike primjenjuje neovisno 

od prethodnih zakona. U tom smislu ga se neće uzimati u skup osnovnih jednadžbi, nego 

će ga se primjenjivati po potrebi (ukoliko postoji potreba za ispitivanjem fizikalnosti 

rješenja). 

Skup jednadžbi osnovnih zakona dinamike fluida 

U skup osnovnih zakona dinamike fluida spadaju opisani zakoni: očuvanja mase, količine 

gibanja, momenta količine gibanja, očuvanja energije i drugi zakon termodinamike. Dani 

matematički zapisi navedenih zakona vrijede uz pretpostavku hipoteze kontinuuma, 

homogenog, jednofaznog i kemijski inertnog fluida u kojem nema površinskih i masenih 

momenata. Kao što je rečeno, za taj se slučaj zakon momenta količine gibanja svodi na 

činjenicu simetričnosti tenzora naprezanja, te, ako se ta simetričnost unaprijed pretpostavi, 

jednadžbu momenta količine gibanja se ispušta iz skupa osnovnih diferencijalnih 

jednadžbi, jer ne nosi nikakvu novu informaciju u odnosu na jednadžbu količine gibanja. 

Drugi zakon termodinamike, je kao što je rečeno pasivna jednadžba, te se ni ona ne mora 

uključiti u osnovni skup jednadžbi, te od skupa osnovnih zakona koji opisuju strujanje 

fluida ostaju: 

-zakon očuvanja mase (jednadžba kontinuiteta) 

∂ ρ ∂( 

ρv 

j ) 

=− 

∂t ∂xj 

-zakon količine gibanja (jednadžba količine gibanja) 

∂( 

ρv 

) ∂ i ( ρvv j i) ∂σ 

ji 

=− + ρ fi 

+ 


-zakon očuvanja energije (energijska jednadžba) 

∂( ρe) 

∂( ρve j ) ∂( 

σ jivi) ∂qi 

=− + ρ fv i i+ 

− 

∂t ∂xj ∂xj ∂ xi 

Jednadžba količine gibanja je vektorska jednadžba (koja se može razložiti na tri skalarne 

jednadžbe), a jednadžba kontinuiteta i energijska jednadžba su skalarne jednadžbe, tako da 

sustav jednadžbi označuju sustav pet skalarnih jednadžbi. U tim jednadžbama poznata je 

gustoća masenih sila f i , a nepoznata polja su: polje gustoće ρ , tri komponente vektorskog


polja brzine v i , šest komponenti simetričnog tenzora naprezanja σ ji , energije e i tri 

komponente vektora površinske gustoće snage toplinskog toka i 

q , što čini 14 nepoznatih 

polja. Očit je nesklad u broju jednadžbi i broju nepoznatih polja, te navedeni sustav ne 

može jednoznačno opisati strujanje fluida. Univerzalni zakoni fizike koji vrijede za sve 

fluide bez obzira na njihovu vrstu i stanje nisu u stanju jednoznačno opisati strujanje 

fluida, te je u cilju usklađivanja broja jednadžbi i broja nepoznatih polja nužno uvesti 

dopunske pretpostavke o reološkim i termodinamičkim svojstvima fluida. Te dopunske 

relacije nemaju univerzalni karakter, te će tako zatvoreni sustav jednadžbi biti valjan samo 

za određenu kategoriju fluida.

Odnosi za savršeni plin 


KONSTITUTIVNE (DOPUNSKE) JEDNADŽBE 

Za toplinsko i kalorički savršeni plin vrijedi toplinska jednadžba stanja: 

p 

= RT 

ρ 

i kalorička jednadžba stanja: 

u = cT v 

pri čemu su specifični toplinski kapaciteti pri konstantnom tlaku i konstantnom volumenu 

konstantni, pa je i njihov odnos konstantan ( c p =konst., c v =konst., κ = cp/ cv=konst.). 

Fourierov zakon toplinske vodljivosti 

Fourierov zakon toplinske vodljivosti uspostavlja linearnu vezu između vektora površinske 

gustoće toplinskog toka i gradijenta temperature, koja uz pretpostavku izotropnosti fluida, 

poprima oblik: 

q 

i 

∂T 

= −λ 

∂x 

i 

U gornjem izrazu je λ toplinska provodnost fluida ([ ] W/ ( m K) 

λ = ⋅ ), pozitivna je 

SI 

veličina i funkcija je lokalnog termodinamičkog stanja. Predznak minus na desnoj stani 

izraza označuje da će toplina spontano prelaziti uvijek s mjesta više temperature prema 

mjestu s nižom temperaturom, dakle u smjeru suprotnom gradijentu temperature, što znači 

da su vektori toplinskog toka i gradijenta temperature suprotno usmjereni kolinearni 

vektori. 

Newtonov zakon viskoznosti 

Newtonov zakon viskoznosti uspostavlja linearnu vezu između simetričnog tenzora 

naprezanja i tenzora brzine deformacije (simetričnog dijela gradijenta brzine). Polazeći od 

činjenice da u mirujućem plinu vlada termodinamički tlak p, a da su tangencijalna 

naprezanja jednaka nuli, tenzor naprezanja se može prikazati u obliku: 

σ =− pδ + Σ 

ji ji ji 

gdje je δji jedinični tenzor, a Σji simetrični tenzor viskoznih naprezanja, koji se uz 

pretpostavku izotropnosti fluida, modelira izrazom: 

⎛ ∂v j ∂v ⎞ 

i ⎛ 2 ⎞ ∂vk 

⎛ 2 ⎞ 

Σ = μ⎜ + + μ − μ δ = 2μD + μ − μ D δ 

⎜ 

⎟ 

xi x ⎟ ⎜ ⎟ ⎜ ⎟ 

⎝ ∂ ∂ j ⎠ ⎝ 3 ⎠ ∂xk 

⎝ 3 ⎠ 

ji V ji ji V kk ji 

U gornjem izrazu je μ dinamička viskoznost, V 

μ volumenska viskoznost, a Dji tenzor 

brzine deformacije. Kontrakcijom indeksa u gornjem izrazu i njegovim dijeljenjem s tri, 

slijedi:

1 

σ jj =− p + μV 

3 


∂vk 

∂x 

�k 

1 D(d V ) 

dV Dt 

Lijeva strana gornjeg izraza je srednje mehaničko naprezanje, čija se negativna vrijednost 

naziva i mehaničkim tlakom, a koji se razlikuje od termodinamičkog tlaka za član koji je 

razmjeran volumenskoj viskoznosti i relativnoj brzini promjene volumena čestice fluida. 

Utjecaj volumenske viskoznosti je značajan u strujanjima sa značajnim gradijentima 

gustoće fluida, kao što su eksplozije i udarni valovi. Volumenska viskoznost jednoatomnih 

plinova jednaka je nuli, a u strujanjima gdje je brzina promjene volumena čestica fluida 

(odnosno gustoće fluida) mala koeficijent volumenske viskoznosti se može zanemariti. U 

tom slučaju izraz za tenzor viskoznih naprezanja prelazi u: 

⎛ ∂v 

j v ⎞ 

i 2 vk 

2 

Σ ji μ⎜ 

∂ ∂ 

= + ⎟ − μ δ ji = 2μD 

ji − μ D 

⎜ xi 

x ⎟ 

⎝ ∂ ∂ j ⎠ 3 ∂x 

k 

3 

U nestlačivom strujanju je divergencija polja brzine identički jednaka nuli te su viskozna 

naprezanja opisana sljedećim izrazom: 

⎛ ∂v j ∂v 

⎞ 

i 

Σ = μ⎜ + = 2μD 

⎜ 

⎟ 

xi x ⎟ 

⎝ ∂ ∂ j ⎠ 

ji ji 

Viskoznosti μ i μ V su pozitivne veličine, a funkcije su lokalnog termodinamičkog stanja 

fluida. 

OSNOVNE JEDNADŽBE DINAMIKE NEWTONSKOG SAVRŠENOG PLINA 

Treba naglasiti da osnovni zakoni klasične fizike vrijede za sve fluide, a pojedini 

matematički modeli strujanja fluida razlikuju se jedino po dopunskim ili konstitutivnim 

relacijama, koje opisuju specifično ponašanje pojedinih fluida. Uvrštavanjem 

konstitutivnih relacija u jednadžbe osnovnih zakona dobiva se matematički model u kojem 

je broj nepoznatih polja usklađen s brojem jednadžbi, a koji vrijedi samo za fluide koji se 

ponašaju sukladno uvedenim konstitutivnim relacijama. Tako su osnovne jednadžbe 

dinamike newtonskog savršenog plina: 

- jednadžba kontinuiteta 

∂ρ 

∂( 

ρv 

j ) 

=− 

∂t ∂x 

j 

- jednadžba količine gibanja 

∂( ρvi 

) 

∂t ∂( ρvv) 

∂p 

=− + ρ fi 

− 

∂x ∂x + 

∂Σ 

∂x 

j i ji 

j i j 

, gdje je 

⎛ ∂v j ∂v ⎞ 

i ⎛ 2 ⎞ ∂vk 

⎛ 2 ⎞ 

Σ = μ⎜ + + μ − μ δ = 2μD + μ − μ D δ 

⎜ 

⎟ 

xi x ⎟ ⎜ ⎟ ⎜ ⎟ 

⎝ ∂ ∂ j ⎠ 

⎝ 3 ⎠ ∂xk 

⎝ 3 ⎠ 

ji V ji ji V kk ji 

kk 

δ 

ji

- energijska jednadžba 


( pv ) ∂( 

Σ jivi ) 

2 2 

∂ ⎡ ⎛ v ⎞⎤ ∂ ⎡ ⎛ v ⎞⎤ 

∂ i 

∂ ⎛ ∂T 

⎞ 

⎢ρ⎜ + u⎟⎥ =− ⎢ρvj⎜ + u⎟⎥+ ρ fv i i − + + ⎜λ ⎟ 

∂t ⎣ ⎝ 2 ⎠⎦ ∂xj ⎣ ⎝ 2 ⎠⎦ ∂xi ∂xj ∂xi ⎝ ∂xi 

⎠ 

- toplinska jednadžba stanja 

p = ρRT 

- kalorička jednadžba stanja 

u = cVT 

Navedeni sustav jednadžbi je sustav sedam jednadžbi u kojima se pojavljuje sedam 

nepoznatih polja ( ρ , vj, p, u i T ). Uz zadane početne i rubne uvjete, ovaj sustav 

jednoznačno opisuje problem strujanja newtonskog savršenog plina. Naravno, zbog 

nelinearnosti (npr. konvekcijski član u jednadžbi količine gibanja - prvi član desne strane) 

uglavnom se neće moći naći analitičko rješenje postavljenog sustava, nego će za njegovo 

rješavanje trebati primijeniti numeričke metode. Pojavom računala, došlo je do razvoja 

računalne dinamike fluida (Computational Fluid Dynamics- CFD), grane unutar mehanike 

fluida, koja obuhvaća metode numeričkog rješavanja gornjeg sustava jednadžbi. 

MATEMATIČKI MODEL NESTLAČIVOG STRUJANJA 

Posebnu klasu strujanja čine nestlačiva strujanja, u kojima gustoća fluida tijekom strujanja 

ostaje konstantna. To se uglavnom odnosi na strujanje kapljevina, iako u strujanjima s 

velikim gradijentima tlaka (npr. podvodna eksplozija) može doći do razlike u gustoći 

kapljevina (jer su i kapljevine stlačive) tako da bi strujanje trebali promatrati kao stlačivo. 

S druge strane i strujanje plinova (koji su izričito stlačivi) pri malim brzinama strujanja u 

odnosu na brzinu zvuka, možemo smatrati nestlačivim. Tako npr. strujanje zraka u 

ventilacijskom kanalu brzinom do desetak metara u sekundi, uzrokuje vrlo mali pad tlaka 

(svega nekoliko paskala) po jedinici duljine kanala. Ako se uzme da je tlak zraka reda 

veličine atmosferskog tlaka (dakle reda veličine 100000 Pa), a strujanje približno 

izotermičko, onda je iz jednadžbe stanja jasno da zbog pada tlaka neće doći do značajne 

promjene gustoće zraka, pa se takvo strujanje također opisuje modelom nestlačivog 

strujanja. U nestlačivom strujanju se dakle toplinska jednadžba stanja p = ρRT 

zamjenjuje 

s ρ = konst. , čime se gubi zavisnost gustoće od temperature (odnosno unutarnje energije) 

fluida. Ako se može zanemariti promjena viskoznosti fluida o temperaturi, tada jednadžba 

kontinuiteta i jednadžba količine gibanja postaju posve nezavisne od temperature. U tom 

se slučaju rješavanjem tih dviju jednadžbi dolazi do polja tlaka i brzine, a nakon toga se 

rješava energijska jednadžba (koja, osim kalorijske jednadžbe stanja ostaje jedina 

jednadžba u kojoj se pojavljuje temperatura) čime se dolazi do polja temperature (odnosno 

specifične unutarnje energije). Ako nas polje temperature ne zanima energijsku jednadžbu 

ne moramo niti rješavati. Jednadžbe koje opisuju nestlačivo strujanje uz μ =konst. su: 

- jednadžba kontinuiteta 

∂v 

j 

∂x 

∂v1 = 0 ili 

∂x + 

∂v2 ∂x + 

∂v3 

∂x 

= 0 

j 

1 2 3


- jednadžba količine gibanja 

∂( ρvi 

) 

∂t ∂( 

ρvv 

j i) 

∂p =− + ρ fi 

− 

∂x ∂x 2 

∂ vi 

+ μ 

∂x ∂x 

j i j j 

Energijsku jednadžbu za slučaj nestlačivog strujanja ćemo kasnije definirati. 

Početni i rubni uvjeti 

Dani sustav jednadžbi opisuje nestlačivo strujanje bilo kojeg newtonskog fluida, u bilo 

kakvom geometrijskom području. Kad bi znali analitički integrirati ove jednadžbe, dobili 

bismo njihovo opće analitičko rješenje u kojem bi se pojavile određene funkcije 

integracije, koje bi činile opće rješenje neodređenim, sve dok se ne zada područje u kojem 

se neko strujanje analizira, uvjeti koji vladaju u tom području u početnom trenutku 

integracije (početni uvjeti), kao i uvjeti koji vladaju na rubu tog područja tijekom vremena 

integracije (rubni uvjeti). Ako nas zanima samo stacionarno rješenje (rješenje koje se 

dobije kad iščeznu sve vremenske promjene), početne uvjete nije potrebno zadavati. 

Tipični rubni uvjeti za brzinu 

1) Rubni uvjet na nepropusnoj stijenci. 

Viskozni fluid se lijepi na stijenku, tako da je brzina fluida na stijenci jednaka brzini 

stijenke (nema relativne brzine između fluida i stijenke, kao što je to bio slučaj u 

potencijalnom strujanju). Jasno je da je na mirujućoj stijenci brzina fluida jednaka nuli. 

2) Rubni uvjet na granici dvaju fluida. 

Ako se dva fluida (različitih gustoća i viskoznosti) koja se ne miješaju, gibaju 

laminarno svaki u svom sloju, pri čemu se slojevi dodiruju, tada se dodirna površina 

ponaša kao nepropusna stijenka, na kojoj nema relativne brzine između dva sloja. Po 

principu akcije i reakcije slojevi djeluju jedan na drugoga istom silom po veličini 

suprotnom po predznaku, što znači da su površinske sile na dodirnoj granici 

neprekidne. 

3) Rubni uvjet na slobodnoj površini. 

Slobodna površina je u principu razdjelna površina dvaju fluida, od kojih jedan ima 

puno manju gustoću i viskoznost od drugoga (primjer strujanje vode u kanalu – gustoća 

i viskoznost zraka su za tri reda veličine manji od gustoće i viskoznosti vode). U tom 

se slučaju viskozne sile u fluidu s malom viskoznošću (u spomenutom primjeru u 

zraku) mogu zanemariti, pa rubni uvjet na slobodnoj površini prelazi u uvjet nultog 

smičnog naprezanja. U takvoj se situaciji promatra strujanje samo u fluidu veće 

gustoće ( u spomenutom primjeru u vodi). 

Potencijalna energija 

ALTERNATIVNI OBLICI ENERGIJSKE JEDNADŽBE 

Kao što je poznato iz mehanike, rad (snagu) potencijalne masene sile se može prikazati 

promjenom (brzinom promjene) potencijalne energije. Ako se sa eP označi masena gustoća 

potencijala specifične masene sile (npr. potencijalna energija za silu težine (gravitacije) je 

EP = mgz = mgx3, 

a specifični potencijal je eP = EP/ m= gz = gx3), 

pri čemu taj potencijal 

nije vremenski promjenjiv, tada se specifična masena sila može prikazati gradijentom tog 

potencijala:

∂eP 

fi 

=− 

∂x 

i 


na primjer za silu gravitacije: 

( gx ) 

∂ 

f = − =− gδ= −g 

3 

i 

∂xi 

3i 

( 0,0, ) 

Uzimajući u obzir gornju definiciju, član koji označuje snagu masenih sila u energijskoj 

jednadžbi, može se pisati u obliku: 

∂eP∂ ∂( 

ρvi 

) 

ρ fv i i=− ρ vi=− ( ρve 

i P) + eP 

∂xi ∂xi ∂xi 

�� 

∂ρ 

prema JK =− 

∂t 

Ako se u zadnjem članu gornje jednadžbe primijeni jednadžba kontinuiteta kao što je 

naznačeno, te uzme u obzir da e P nije funkcija vremena, slijedi: 

( ρ ) ( ρ ) 

⎡ ∂ e ∂ ve ⎤ De 

ρ fv i i=− 

⎢ + ⎥ =−ρ 

⎣ ∂t ∂xi⎦ 

Dt 

P i P P 

U gornjem izrazu je iskorišteno pravilo B (vidjeti prethodna predavanja) za prijelaz s 

konzervativnog na nekonzervativni zapis. Riječima iskazan, gornji izraz glasi: Snaga 

vanjske potencijalne masene sile koja djeluje na česticu fluida jednaka je negativnoj brzini 

promjene potencijalne energije čestice fluida. Dakle pozitivna snaga masene sile tj. gibanje 

čestice fluid u smjeru masene sile (npr. gibanje čestice prema dolje u polju gravitacije) 

označuje smanjenje potencijalne energije, i obrnuto kada je skalarni umnožak fiv i 

negativan, to označuje povećanje potencijalne energije čestice fluida. Uvrštavanjem 

gornjeg izraza za snagu masenih sila u energijsku jednadžbu, ona prelazi u oblik: 

⎡ ⎛ 2 

∂ v 

⎢ ⎜ 

+ u + e 

∂t 

⎢⎣ 

⎝ 2 

⎞⎤ 

⎡ ⎛ 2 

∂ v ⎞⎤ 

∂ 

⎟ ⎢ ⎜ ⎟ 

i 

⎟⎥ 

= − ρv 

j ⎜ 

+ u + e 

⎟⎥ 

− 

⎠⎥⎦ 

∂x 

j ⎢⎣ 

⎝ 2 ⎠⎥⎦ 

∂xi 

ρ P 

P 

( pv ) ∂( 

Σ jivi 

) 

u kojem se pojavljuje zbroj kinetičke, unutarnje i potencijalne energije. 

Jednadžba kinetičke i unutarnje energije 

+ 

∂x 

j 

+ 

∂ 

∂x 

i 

⎛ ∂T 

⎞ 

⎜ 

⎜λ 

⎟ 

⎝ ∂xi 

⎠ 

U prethodnom obliku energijske jednadžbe smo vidjeli da pri strujanju fluida u polju 

potencijalne sile pod ukupnom energijom možemo promatrati zbroj triju oblika energije, 

što je zgodno u integralnom pristupu rješavanja problema. U diferencijalnom pristupu 

ćemo uvijek težiti najjednostavnijem obliku energijske jednadžbe. Kao što smo vidjeli iz 

modela nestlačivog strujanja, polje brzine i tlaka su određeni jednadžbom kontinuiteta i 

jednadžbom količine gibanja, a kada je poznato polje brzine uvijek možemo odrediti 

kinetičku energiju fluida. Stoga se samo od sebe nameće kao ideja da se iz energijske 

jednadžbe eliminira kinetičku energiju fluida. To se može učiniti na način da se od 

energijske jednadžbe oduzme jednadžba kinetičke energije. 

Kao što je poznato iz mehanike jednadžba kinetičke energije se dobije skalarnim 

množenjem jednadžbe količine gibanja s brzinom. Primijenjeno na nekonzervativni oblik 

jednadžbe količine gibanja u diferencijalnom obliku dobije se 

Dvi∂p 

∂Σ 

ji 

ρvi = ρ fv i i − vi + vi 

�� 

Dt 

∂xi ∂xj 

2 

D ⎛ v ⎞ 

⎜ 

Dt⎜ ⎟ 

2 ⎟ 

⎝ ⎠


Podsjetimo se fizikalnog značenja članova s površinskim silama. Član ∂p/ ∂ xi 

označuje 

rezultantnu silu tlaka na česticu fluida, a njen skalarni umnožak s vektorom brzine 

označuje snagu tlačnih sila kojom se mijenja kinetička energija fluida. Ako je polje tlaka 

konstantno, onda je i rezultantna sila tlaka na česticu fluida jednaka nuli (sjetimo se statike 

fluida u MFI – sila konstantnog tlaka na zatvorenu površinu jednaka je nuli) pa je doprinos 

toga člana kinetičkoj energiji fluida jednak nuli. Zadnji član gornje jednadžbe je skalarni 

umnožak rezultantne viskozne sile na česticu fluida s brzinom čestice, tj. označuje 

doprinos viskoznih sila promjeni kinetičke energije čestice fluida. 

Ako se u nekonzervativnom zapisu energijske jednadžbe deriviraju članovi koji označuju 

površinske sile dobije se 

2 

D ⎛ v ⎞ 

∂p 

∂v ∂Σ 

i ji ∂vi ∂ ⎛ ∂T 

⎞ 

ρ ⎜ + u⎟= ρ fv i i−vi − p + vi 

+ Σ ji + ⎜λ⎟ Dt 

⎝ 2 ⎠ 

∂xi ∂xi ∂xj ∂xj ∂xi ⎝ ∂xi⎠ 

pri čemu su plavom bojom označeni članovi koji se pojavljuju u jednadžbi kinetičke 

energije. Oduzimanjem jednadžbe kinetičke energije od jednadžbe ukupne energije 

(energijske jednadžbe) dobije se jednadžba unutarnje energije (članovi označeni crvenom 

bojom u gornjoj jednadžbi), koja glasi 

Du ∂vi ∂vi ∂ ⎛ ∂T⎞ 

ρ =− p + Σ ji + ⎜λ ⎟, 

Dt ∂xi ∂xj ∂xi ⎝ ∂xi 

⎠ 

koja u konzervativnom obliku (dobije se primjenom pravila B iz prethodnih predavanja) 

glasi: 

∂( ρu) 

∂( 

ρvu 

j ) ∂vi ∂vi ∂ ⎛ ∂T 

⎞ 

=− − p + Σ ji + ⎜λ⎟ ∂t ∂xj ∂xi ∂xj ∂xi ⎝ ∂xi 

�� 

⎠ 

( V ) Φv 

p Dd ≥0 

dV Dt 

Iz termodinamike je poznato da je izraz za mehanički rad u ravnotežnom procesu jednak 

p dV 

− pdV , te bi snaga bila − pd V /dt, 

a volumenska gustoća te snage − . U mehanici 

V dt 

fluida se sukladno principu lokalne ravnoteže za termodinamički sustav uzima čestica 

fluida ( V → dV 

), a vremensku promjenu koja se odnosi na česticu fluida (materijalnu 

derivaciju) se označuje s D/Dt , pa je jasno da član − p∂vi/ ∂ xi 

u jednadžbi unutarnje 

energije označuje volumensku gustoću snage sile tlaka koja doprinosi promjeni unutarnje 

energije. Pri ekspanziji se volumen čestice fluida povećava ( dV > 0), 

a njena se unutarnja 

energija smanjuje, što znači da čestica vrši rad prema svojoj okolini. Pri kompresiji je 

dV < 0 (volumen čestice fluida se smanjuje) pa se unutarnja energija čestice fluida 

povećava, što znači da se čestici dovodi rad iz njene okoline. Iz rečenog je jasno da se 

putem tlačnih sila mehanička energija može pretvarati u unutarnju i obrnuto. 

Član Φ v u jednadžbi unutarnje energije označuje volumensku gustoću snage viskoznih sila 

koja doprinosi promjeni unutarnje energije. Ako se gradijent brzine ∂vi/ ∂ xj 

prikaže 

zbrojem simetričnog tenzora brzine deformacije D ji i antisimetričnog tenzora vrtložnosti 

V ji , uzimajući u obzir da je dvostruki skalarni produkt simetričnog i antisimetričnog 

tenzora jednak nuli, može se pisati: 

∂vi 

Φ v = Σ ji = Σ ji( Dji + Vji) = Σ jiD ji 

∂x 

j


Ako se u gornji izraz za viskozna naprezanja uvrsti Newtonov zakon viskoznosti, gornji 

izraz za volumensku gustoću snage viskoznih sila, nakon razvoja po nijemim indeksima, 

prelazi u oblik: 

Φv = Σ jiDji= 2 

2 2 2 

μ⎡( D11− D22) + ( D22 − D33) + ( D33− D11) 

⎤+ 

3 ⎣ ⎦ 

2 

+ 4μ D 

2 

+ D 

2 

+ D + μV 

D + D + D 

( ) ( ) 2 

12 

13 

23 

S obzirom da su koeficijenti viskoznosti pozitivne veličine, iz gornjeg je izraza jasno da je 

snaga viskoznih sila uvijek pozitivna veličina, što fizikalno znači da će se unutarnja 

energija čestice fluida zbog djelovanja viskoznih sila uvijek povećavati. Ako se gleda 

ukupna energija izoliranog sustava, onda je jasno da to povećanje može ići jedino na račun 

mehaničke energije. Viskozna pretvorba mehaničke u unutarnju energiju traje sve dok 

postoji gradijent brzine. 

U nestlačivom strujanju je divergencija brzine jednaka nuli, odnosno nema promjene 

volumena čestice fluida, te nema promjene unutarnje energije čestice fluida putem sile 

tlaka, pa jednadžba unutarnje energije prelazi u oblik 

∂( ρu) 

∂( 

ρvu 

j ) ∂ ⎛ ∂T⎞ 

=− + Φv+ ⎜λ ⎟, 

gdje je 

∂t ∂xj ∂xi ⎝ ∂xi 

⎠ 

Φv= Σ jiDji = 2μDjiDji 

Za slučaj nestlačivog strujanja jedini mehanizam izmjene unutarnje i mehaničke energije je 

putem viskoznih sila, a ta je izmjena kako je rečeno uvijek jednosmjerna, tj. uslijed 

viskoznih sila mehanička se energija pretvara u unutarnju, a nikad obrnuto. Takav proces 

je dakle nepovratan, te će prema drugom zakonu termodinamike izazivati porast entropije. 

S obzirom da se u nestlačivom strujanju unutarnja energija ne može pretvoriti u 

mehaničku, ona nema značenja sa stajališta strujanja. Stoga se u analizi nestlačivog 

strujanja razmatra samo mehanička energija, a brzina pretvorbe mehaničke energije u 

unutarnju se naziva gubicima mehaničke energije (vidjeti hidraulički proračun cjevovoda u 

MFI). 

Primjenom kaloričke jednadžbe stanja jednadžba unutarnje energije se može prevesti u 

temperaturnu jednadžbu, koja je za savršeni plin oblika: 

DT 

∂vi ∂vi ∂ ⎛ ∂T 

⎞ 

ρcV =− p + Σ ji + ⎜λ ⎟ 

Dt 

∂xi ∂xj ∂xi ⎝ ∂xi 

�� 

⎠ 

Φ 

Za nestlačivo strujanje temperaturna jednadžbe prelazi u oblik 

ρcV DT 

Dt 

= 

∂( ρcT 

V ) 

+ 

∂t ∂( 

ρvcT 

j V ) 

∂xj = Φv + 

∂ 

∂xi ⎛ ∂T 

⎜λ ⎝ ∂xi 

⎞ 

⎟ 

⎠ 

v 

U krutim tijelima, gdje nema deformacije čestica zbog vi ≡ 0 , temperaturna jednadžba se 

svodi na poznatu jednadžbu provođenja topline, koja glasi: 

∂T ∂ ⎛ ∂T ⎞ ∂ ⎛ ∂T ⎞ ∂ ⎛ ∂T ⎞ ∂ ⎛ ∂T 

⎞ 

ρc= ⎜λ ⎟= ⎜λ ⎟+ ⎜λ ⎟+ 

⎜λ ⎟ 

∂t ∂xi ⎝ ∂xi ⎠ ∂x1 ⎝ ∂x1 ⎠ ∂x2 ⎝ ∂x2 ⎠ ∂x3 ⎝ ∂x3 

⎠ 

11 

22 

33


Naravno, u izvodu prethodne jednadžbe nije uzeta u obzir mogućnost postojanja toplinskih 

izvora raspodijeljenih po volumenu fluida. Za slučaj konstantne toplinske provodnosti, 

jednadžba se može pisati u obliku 

2 

∂T λ ∂ T 

= 

∂t � 

ρc 

∂xi∂xi a 

gdje je a temperaturna provodnost. Za slučaj stacionarnog provođenja topline dobije se 

polje temperature koje je opisano Laplaceovom jednadžbom. 

2 

∂ T 

= 0 

∂xi∂xi Dakle stacionarno provođenje topline i potencijalno strujanje su analogne pojave, pri čemu 

temperatura odgovara potencijalu brzine, a vektor toplinskog toka podijeljen s toplinskom 

provodnošću odgovara vektoru brzine. 

Drugi zakon termodinamike i produkcija entropije 

Promjena entropije čestice fluida, kao elementarnog termodinamičkog sustava, definirana 

je izrazom 

ρT Ds Dt Du 

= ρ 

Dt 

∂v 

j 

+ p 

∂xj 

Ako se u gornji izraz uvrsti jednadžba unutarnje energije on prelazi u oblik: 

Ds ρ 

Dt 

Φ v = 

T 

1 

+ 

T 

∂ 

∂xi ⎛ ⎞ 

⎜ ∂T 

⎟ 

⎜λ ⎟ 

⎜ ∂xi 

⎟ 

⎜��⎟ ⎝ −qi 

⎠ 

Jednadžba ukazuje da do promjene entropije čestice fluida dolazi zbog djelovanja 

viskoznih sila (prvi član desne strane jednadžbe) na česticu fluida, te zbog izmjene topline 

(drugi član desne strane) čestice fluida s okolinom. Kao što je pokazano Φ v je uvijek 

pozitivan, što znači da će uvijek izazvati porast entropije, što se za jedan spontani proces i 

očekuje. Izmjena topline čestice fluida također mijenja njenu entropiju, pri hlađenju 

čestice, entropija joj opada, a pri grijanju raste. 

Za ocjenu ima li u promatranom sustavu uzroka nepovratnosti procesa poslužit će 

produkcija entropije (vidjeti koncept iz termodinamike u 3. predavanjima), a za brzinu 

produkcije entropije vrijedi 

Ds 

∂ ⎛ qi 

⎞ 

σ = ρ + ⎜ ⎟ ≥ 0 

Dt 

∂x 

⎝ T ⎠ 

i 

Uvrštavanjem izraza za promjenu entropije čestice fluida u gornji izraz, slijedi: 

2 

Φvλ ⎛ ∂T 

⎞ 

σ = + 2 ⎜ ⎟ 

T T ⎝ ∂xi⎠ 

Iz gornjeg izraza je očito da će brzina produkcije entropije uvijek biti pozitivna veličina, a 

jednaka je nuli samo za neviskozno ( μ = μv 

= 0 ) i adijabatsko (λ=0) strujanje. Pod tim 

uvjetima strujanje će biti izentropsko i povratno.


TEORIJA SLIČNOSTI 

Mehanika fluida je teorijsko-eksperimentalna znanost, unutar koje se dugi niz godina do 

praktičnih rezultata dolazilo eksperimentalnim putem. Mjerenja (eksperimenti) se općenito mogu 

vršiti u originalnoj pojavi (prototipu) ili u modelskoj pojavi (modelu). Dimenzijska analiza, 

polazeći od pretpostavljenog skupa utjecajnih veličina, daje podloge za organizaciju 

eksperimenta u smislu minimiziranja potrebnog broja mjerenja i olakšavanja prikaza dobivenih 

rezultata. Teorija sličnosti, polazeći od sustava jednadžbi koji opisuje promatranu pojavu, daje 

podlogu za modelska istraživanja (kriterije koje treba zadovoljiti da bi se rezultati s modelske 

pojave mogli preslikati na prototipnu pojavu) kako u mehanici fluida, tako i u svim ostalim 

granama fizike i tehnike. 

Razlog za modelska istraživanja može biti neki od sljedećih 

1. Skupa izrada prototipa (npr. u brodogradnji i avioindustriji se izrađuju modeli broda i 

aviona koji se ispituju u bazenu, odnosno zračnom tunelu) 

2. Visoke temperature u prototipnoj pojavi (pribjegava se modelu u kojem će temperature 

biti niže). 

3. U prototipnoj pojavi je eksplozivni ili otrovni plin (u modelskoj pojavi se uzima 

neeksplozivni, neotrovni plin) 

4. Prototipna pojava se odvija prebrzo sa stajališta mjernih instrumenata (pojava se 

modelira da traje dugo u vremenu) 

5. itd. … 

Modelska istraživanja 1 imaju smisla samo ako se iz rezultata dobivenih na modelu mogu točno 

predvidjeti rezultati na prototipu, tj. pojave moraju biti slične 2 . 

Definicija sličnosti dvaju pojava: 

Za dvije fizikalne pojave kaže se da su slične ako su opisane istim fizikalnim zakonima i 

ako se veličine u jednoj fizikalnoj pojavi (npr. na prototipnoj) mogu odrediti iz veličina 

druge fizikalne pojave (npr. modelske) jednostavnim množenjem konstantom koja se 

naziva koeficijentom sličnosti. 

Ako ϕ označava neku od fizikalnih veličina prve pojave (npr. prototipne), a ϕ′ istovjetnu 

fizikalnu veličinu u drugoj pojavi (npr. modelskoj), tada prema definiciji sličnosti vrijedi: 

ϕ = Cϕϕ′ (1) 

1 

Teorija sličnosti također daje podlogu i za primjenu metode analogije. Za dvije pojave iz 

različitih grana fizike se kaže da su analogne ako su opisane istim oblikom jednadžbe. Tako je 

2 2 

npr. potencijalno strujanje fluida opisano Laplaceovom jednadžbom ∂ ϕ / ∂ xi 

= 0, 

a polje 

temperature u krutini s konstantnom toplinskom provodnošću λ , također Laplaceovom 

2 2 

jednadžbom ∂ T/ ∂ xi= 

0. 

Očito postoji analogija između potencijala brzine i temperature, te 

brzine strujanja fluida vi =∂ϕ/ ∂ xi 

i vektora toplinskog toka − qi/ λ =∂T / ∂ xi. 

Tako za svako 

rješenje Laplaceove jednadžbe za polje temperature postoji analogno rješenje potencijalnog 

strujanja fluida. 

2 

Pojavom računala dolazi do naglog razvoja računalne dinamika fluida (engl. Computational 

Fluid Dynamics – CFD), u kojoj se do rezultata dolazi numeričkim rješavanjem teorijskih 

jednadžbi koje opisuju strujanje fluida. Ovdje izložena teorija sličnosti valjana je (može se 

primijeniti) i za preslikavanje rezultata proračuna s jedne na drugu sličnu situaciju.

gdje je C ϕ koeficijent sličnosti za veličinu ϕ . 

x1 

x3 

O 

x2 

L 


M(x1,x2,x3,t) 

v � 

a) Prototipna pojava b) Modelska pojava 

Ako su ϕ i ϕ′ vektorske veličine (npr. vektori v � i v′ 

� , prema slici) tada će ti vektori u 

promatrane dvije pojave biti međusobno paralelni, a mogu se razlikovati samo po veličini, tj 

vrijedi vi = Cvv′ i, 

gdje je konstanta C v koeficijent sličnosti za vektorsku veličinu v � . Svakoj 

vremensko prostornoj točki M u prototipnoj pojavi odgovara analogna vremensko prostorna 

točka M′ u modelskoj pojavi. Prostorne koordinate se preslikavaju s pomoću koeficijenta 

sličnosti za duljinu (koji se obično označuje s L C ): xi = Cx′ L i , a vrijeme se preslikava s pomoću 

koeficijenta sličnosti za vrijeme t = Ct′ t . Ako su ϕ i ϕ′ polja fizikalnih veličina koja su funkcije 

prostornih i vremenske koordinate, tada relacija ϕ = Cϕϕ′ vrijedi za bilo koje dvije točke M i 

M′, u kojima su polja fizikalne veličine definirana. 

Karakteristična vrijednost fizikalne veličine 

Svakoj fizikalnoj veličini ϕ se može pridružiti njena karakteristična vrijednost Φ . 

Karakteristična vrijednost se obično definira iz rubnih uvjeta koji definiraju pojavu, moguće je tu 

vrijednost definirati kao vrijednost u odabranoj točki M . Ako se sa Φ označi karakterističnu 

vrijednost veličine ϕ , definiranu kao vrijednost polja ϕ u nekoj točki M, a sa Φ ′ 

karakterističnu veličinu polja ϕ′ , tj. vrijednost polja ϕ′ u odgovarajućoj prostorno vremenskoj 

točki M′, tada prema izrazu ϕ = Cϕϕ′ vrijedi: 

Φ = CϕΦ′ (2) 

Naravno, ako se radi o duljini, za karakterističnu vrijednost se obično odabire neka od 

karakterističnih dimenzija, npr. duljina L , prema gornjoj slici. Iz gornje jednadžbe slijedi da je 

koeficijent sličnosti definiran omjerom karakterističnih vrijednosti veličina dviju pojava: 

Φ 

Cϕ = (3) 

Φ′ 

Tako bi koeficijent sličnosti za duljinu (često se iskazuje i kao mjerilo modela) bio CL= L/ L′ . 

Naravno, ako su ϕ i ϕ′ vektorska polja, karakteristične vrijednosti Φ i Φ ′ označuju apsolutne 

vrijednosti (intenzitete) vektorskih veličina. 

x′1 

x′3 

O′ 

L′ 

x′2 

v ′ 

� 

M′(x′1,x′2,x′3,t′)


Bezdimenzijska polja fizikalnih veličina 

Uvrštavanjem izraza Cϕ = Φ / Φ′ u izraz ϕ = Cϕϕ′ on prelazi u oblik: 

ϕ ϕ′ 

= = � ϕ 

(4) 

Φ Φ′ 

gdje je sa ϕ ~ označena bezdimenzijska vrijednost polja ϕ i ϕ′ . Iz tog se izraza zaključuje da su 

u dvjema sličnim pojavama sva bezdimenzijska polja ista, odnosno da su sve bezdimenzijske 

veličine u modelskoj i prototipnoj pojavi iste. 

Poznavajući bezdimenzijsko polje ϕ ~ lako se dolazi do polja ϕ i ϕ′ : 

ϕ = Φ ~ ϕ i ϕ ′ = Φ ′ ~ ϕ 

(5) 

Naravno da bezdimenzijsko polje vrijedi ne samo za dvije pojave, nego za cijelu obitelj sličnih 

pojava koje zadovoljavaju iste kriterije sličnosti. 

Teorem sličnosti 

Bezdimenzijsko rješenje nekog problema definirano je bezdimenzijskim jednadžbama i 

bezdimenzijskim početnim i rubnim uvjetima, iz čega se zaključuje: 

Dvije će pojave biti slične, ako su opisane istim bezdimenzijskim jednadžbama i istim 

bezdimenzijskim početnim i rubnim uvjetima. 

Postupak određivanja kriterija sličnosti 

Do kriterija sličnosti dvaju pojava dolazi se svođenjem sustava jednadžbi koji opisuje 

promatrane pojave i pripadajućih početnih i rubnih uvjeta u bezdimenzijski oblik. Jasno je da će 

sustavi jednadžbi koji opisuju prototipnu i modelsku pojavu imati isto bezdimenzijsko rješenje 

ako su koeficijenti bezdimenzijskih jednadžbi i bezdimenzijski početni i granični uvjeti isti za te 

dvije pojave. Iz uvjeta jednakosti koeficijenata u bezdimenzijskim jednadžbama prototipne i 

modelske pojave slijede kriteriji sličnosti. 

Postupak određivanja kriterija sličnosti je dakle sljedeći: 

1. Definirati polazne jednadžbe koje opisuju pojavu, te pripadajuće početne i rubne uvjete. 

(Napomena: početni i rubni uvjeti također mogu biti opisani jednadžbom) 

2. Za svaku promjenjivu veličinu ϕ , odnosno ϕ′ u pojavi, temeljem početnih i rubnih 

uvjeta, te konstanti u jednadžbama definirati karakteristične vrijednosti tih veličina Φ 

i Φ ′ , pri čemu vrijedi 

Φ 

ϕ = Φϕ� 

(a) ϕ′ = Φϕ ′ � (b) ϕ = Cϕϕ′ (c) Cϕ = (d) 

′ 

Ako neka od promjenjivih veličina nije definirana u početnim i rubnim uvjetima njena se 

karakteristična vrijednost definira kombinacijom veličina čije se karakteristične 

vrijednosti mogu definirati iz konstanti u jednadžbama, te početnih i rubnih uvjeta (prema 

pravilima dimenzijske analize). 

Primjer 1: ako su rubni uvjeti stacionarni, nema se na temelju čega odrediti karakteristično vrijeme, pa se 

za karakteristično vrijeme uzima odnos karakteristične duljine i karakteristične brzine (ili bilo koja 

kombinacija veličina koja daje dimenziju vremena). 

Primjer 2: Rubnim uvjetima u nestlačivom strujanju nije zadan tlak, pa se za karakteristični tlak uzima 

umnožak karakteristične gustoće i kvadrata karakteristične brzine (ili bilo koja kombinacija veličina koja 

daje dimenziju tlaka). 

Φ


3. U jednadžbama prototipne i modelske pojave dimenzijske veličine zamijeniti 

bezdimenzijskim, prema izrazima (a) i (b), definiranim u prethodnoj točki. U svakoj 

jednadžbi učiniti jedan od koeficijenata jediničnim (dijeljenjem jednadžbe s 

koeficijentom uz član uz koji se želi dobiti jedinični koeficijent). Preostali koeficijenti u 

bezdimenzijskim jednadžbama, te u bezdimenzijskim jednadžbama početnih i rubnih 

uvjeta čine kriterije sličnosti dvaju pojava. 

Alternativno se do kriterija sličnosti može doći tako da se npr. u jednadžbama prototipne 

pojave sve veličine izraze s pomoću veličina modelske pojave, prema izrazu (c), te traže 

uvjeti kada će se jednadžbe prototipne pojave svesti na jednadžbe modelske pojave. 

Dakle, nakon uvrštavanja jednadžbi (c) u jednadžbe za prototipnu pojavu se ponovo u 

svakoj jednadžbi jedan od koeficijenata svede na jedinicu, a preostali koeficijenti koji 

čine umnoške potencija koeficijenata sličnosti, također moraju biti jednaki jedinici, čime 

su definirani kriteriji sličnosti. 

4. Sve bezdimenzijske veličine su u prototipnoj i modelskoj pojavi jednake. Iz te se 

činjenice mogu izvesti veze među koeficijentima sličnosti. 

2 

Primjer 1: Bezdimenzijska površina A/ L 

A 

A A′ 

Vrijedi = , ili 

A′ 

CA 

2 

= = 1, 

odnosno C 2 2 

2 2 

A = CL 

L L′ 

L CL 

2 

L′ 

Primjer 2: (bezdimenzijski) koeficijent sile 

F 

F F′ 

= 

ili 

F′ 

CF 

2 2 2 

= = 1, 

odnosno C 2 2 

F = CρCvCA = CρCvCL 1 2 1 2 

ρvA ρ′′ 

v A′ 

ρ v A CρCvCA 2 

2 2 

ρ′ 

v′ 

A′ 

Primjer 3: (bezdimenzijski) koeficijent momenta 

M M′ 

2 2 3 

= 

, odnosno CM = CCCC ρ v A L = CCC ρ v L 

1 2 1 2 

ρvAL ρ′′ 

v AL ′ ′ 

2 2 

Primjer 4: bezdimenzijski protok Q/ vA 

Q 

3 

Q Q′ 

Q′ 

CQ 

2 CL 

= ili = = 1, 

odnosno CQ = CvCA = C 

vA v′ A′ 

v A CC 

�v 

CL 

= . 

C 

v′ A′ 

v A 

Iz rečenoga je jasno da će broj nezavisnih koeficijenata sličnosti biti jednak broju 

osnovnih dimenzija u nekoj pojavi. 

CL / Ct 

t


Primjer: Potrebno je odrediti kriterije sličnosti za slučaj gibanja tijela duljine L koje se trenutno 

� 

počelo gibati konstantnom brzinom v∞ u mirujućem fluidu gustoće ρ∞ , konstantne viskoznosti 

μ∞ u kojem vlada tlak p∞ . Pretpostavlja se nestlačivo, adijabatsko strujanje fluida. 

g 

L 

L′ 

� 

g � 

ρ′∞ 

ρ∞ 

p∞ 

μ∞ 

x1 

x3 

O 

v∞ � 

a) Prototipna pojava b) Modelska pojava 

Slika 1. Oznake veličina u prototipnoj i modelskoj pojavi 

Slika prikazuje opisanu fizikalnu pojavu. Pri definiranju kriterija sličnosti za ovakvo strujanje u 

prvom koraku se raspisuju polazne jednadžbe, uključujući početne i rubne uvjete. Polazne 

jednadžbe za nestlačivo adijabatsko strujanje su jednadžba kontinuiteta i jednadžba količine 

gibanja, a energijska (temperaturna) jednadžba se u ovom slučaju može rješavati neovisno o ove 

dvije, pa se ovdje neće uzeti u obzir. 

∂v 

∂x 

j 

j 

x2 

= 0 

M(x1,x2,x3,t) 

∂vi ∂vi ∂p ∂ ⎛ ∂v 

⎞ 

i 

ρ∞ =−ρ∞vj −ρ∞gδi3− + μ∞ 

⎜ ⎟ 

∂t ∂xj ∂xi ∂x ⎜ 

j x ⎟ 

⎝∂ j ⎠ 

v � 

U početnom trenutku su fluid i tijelo mirovali, a u samom početnom trenutku je brzina tijela 

postigla konstantnu brzinu. Rubni uvjet na površini tijela kaže da je brzina fluida na toj površini 

jednaka brzini tijela (uvjet lijepljenja fluida). Gornje jednadžbe označuju sustav četiri skalarne 

jednadžbe s četiri nepoznata polja (polje tlaka i tri skalarna polja za tri komponente brzine), čije 

je jednoznačno rješenje definirano početnim i rubnim uvjetima. U tim se jednadžbama 

pretpostavlja da je gravitacija jedina masena sila (vektor gravitacije je konstantan i djeluje u 

negativnom smjeru osi x 3 ) i da je ista u obje pojave. 

U drugom koraku je potrebno za svaku promjenjivu veličinu u strujanju definirati karakterističnu 

vrijednost temeljem početnih i rubnih uvjeta. Promjenjive veličine u gornjim jednadžbama su: 

vrijeme t , prostorne koordinate i x , tlak p i brzina v i . Za karakterističnu vrijednost tlaka usvaja 

se tlak p∞ , za karakterističnu vrijednost brzine se usvaja brzina v∞ gibanja tijela, a za 

karakterističnu duljinu duljina L tijela. Za karakteristično vrijeme nemamo izbor u rubnim 

uvjetima, jer smo definirali da se brzina gibanja tijela trenutno promijenila od stanja mirovanja 

na stanje jednolikog gibanja, pa ćemo karakteristično vrijeme definirati preko duljine L i brzine 

p′∞ 

μ′∞ 

x′1 

x′3 

∞ ′ v� 

O′ 

x′2 

v ′ 

� 

M′(x′1,x′2,x′3,t′) 

(P.1) 

(P.2)


v∞ u obliku τ = L / v∞ 

. Svaka promjenjiva veličina u gornjim jednadžbama koje opisuju i 

prototipnu i modelsku pojavu, može se prikazati preko bezdimenzijskih veličina u obliku 

x 

t 

v 

~ 

~ 

j = Lx 

j , x ′ j = L′ 

x j , odnosno x j Cx′ L j 

= τ 

~ 

t , t′ 

= τ ′ 

~ 

t , odnosno t Ct 

t′ 

j = v v~ 

∞ j , v j v v~ 

∞ j ′ = ′ , odnosno v j Cvv 

′ j 

= p ~ 

∞ p , p p ~ 

∞ p ′ = ′ , odnosno p C p p ′ 

p 

= , C = L/ L′ (D.1) 

L 

= , C t = τ / τ ′ (D.2) 

= , Cv = v∞ 

/ v∞′ 

(D.3) 

= , C p = p∞ 

/ p∞′ 

(D.4) 

Uvrštavanjem izraza (D.1) do (D.4) u jednadžbe (P.1) i (P.2) za prototipnu pojavu, uvažavajući 

da su karakteristične vrijednosti veličina konstante, slijedi sustav jednadžbi u bezdimenzijskom 

obliku koji glasi: 

v ∂v� 

∞ 

L ∂x� 

j 

j 

= 0 

2 

ρ∞v∞∂v�i ρ∞v ∞ ∂v�i p∞∂p� μ∞v∞∂ 

⎛ ∂v� 

⎞ 

i 

=− v� 

j + ρ∞gδ 

i3−+ 

2 ⎜ ⎟ 

τ ∂t�L ∂x�j L ∂x�i L ∂x� ⎜ 

j x ⎟ 

⎝ ∂�j ⎠ 

(B.1) 

(B.2) 

Analogni bezdimenzijski sustav jednadžbi se dobiva i za modelsku pojavu, s jedinom razlikom 

da su koeficijenti jednadžbi koje opisuju modelsku pojavu sastavljeni od karakterističnih veličina 

modelske pojave. Ako se u svakoj jednadžbi modelske i prototipne pojave jedan od koeficijenata 

svede na jedinicu, tada će jednakost jednadžbi podrazumijevati jednakost koeficijenata uz 

odgovarajuće članove. Dijeljenjem jednadžbe (B.2) koeficijentom uz konvekcijski član (član 

koji označuje inercijske sile), sustav jednadžbi (B.1) i (B.2) prelazi u oblik 

∂v� 

∂x� 

j 

j 

= 0 

L ∂v�i ∂v�i gL 

p∞ 

∂p� μ∞ 

∂ ⎛ ∂v� 

⎞ 

i 

= −v� j + δ 2 i3− 

+ 2 

⎜ ⎟ 

v τ t x 

�∞ ∂�∂�j v ρ v x 

�∞ �∞ 

∞ ∂�i ρ∞v∞L 

∂x� ⎜ 

j ∂x⎟ 

⎝ 

�j 

�� ⎠ 

St 2 

1/ 

Fr 

Eu 1/ Re 

(C.1) 

(C.2) 

Iz uvjeta jednakosti bezdimenzijskih koeficijenata u jednadžbi (C.2), koji opisuje prototipnu 

pojavu s odgovarajućih koeficijentima analognoj jednadžbi za modelsku pojavu slijede kriteriji 

sličnosti dvaju strujanja. Jasno je da su ti koeficijenti sastavljeni od sedam karakterističnih 

veličina, uvedenih u jednadžbama (D.1) do (D.4), a to su: L , τ , v∞ , p∞ te konstanti g , ρ∞ , i μ∞ u jednadžbi (C.2). U dimenzijama ovih sedam veličina se pojavljuju tri osnovne dimenzije: 

duljine, vremena i mase, te se prema pravilima dimenzijske analize može izabrati skup od tri 

dimenzijski nezavisne veličine, čijim se dimenzijama mogu opisati dimenzije svih sedam 

veličina, odnosno moguće je definirati četiri bezdimenzijska parametara, koji se ovdje nazivaju 

kriterijima sličnosti. Naravno da je izbor dimenzijski nezavisnog skupa potpuno proizvoljan, a 

da o izbranom skupu zavise oblici bezdimenzijskih parametara. Ako bi se npr. za skup 

dimenzijski nezavisnih veličina izabrao skup: ρ∞ , v∞ , L , tada bi se dobio sljedeći skup 

2 

2 

bezdimenzijskih parametara: v∞ τ / L, 

gL/ v∞ , p∞/( ρ∞v∞ 

) ) i μ∞ /( ρ∞v∞ 

L) 

. Izborom nekog 

drugog dimenzijski nezavisnog skupa došlo bi se do drugih bezdimenzijskih parametara. Isto 

tako, bezdimenzijski koeficijenti u jednadžbi (C.2) su dobiveni dijeljenjem jednadžbi (B.2)


koeficijentom uz konvekcijski član, a da su dijeljene nekim drugim koeficijentom dobili bi se 

neki drugi bezdimenzijski koeficijenti. U nastavku će se tim bezdimenzijskim parametrima 

pridružiti ime i objasniti značenje. 

Na lijevoj strani jednadžbe (C.2), uz nestacionarni član, pojavljuje se koeficijent koji se naziva 

Strouhalovim brojem, te za dvije slične pojave vrijedi: 

L L′ 

L lokalna promjena 

= ili St = St′ , gdje je St = = (K.1) 

v τ v′ 

τ ′ v∞τ konvektivna promjena 

∞ ∞ 

Koeficijent uz član koji označuje masene sile u jednadžbi količine gibanja (C.2), prikazuje se 

Froudeovim brojem, a za dvije slične pojave vrijedi: 

gL gL′ 

= 

v v′ 

2 2 

∞ ∞ 

1 1 

Fr Fr′ 

ili = 2 2 

gdje je 

v∞ 

inercijske sile 

Fr = = (K.2) 

gL gravitacijska sila 

Koeficijent uz gradijent tlaka u jednadžbi količine gibanja (C.2), se u nestlačivom strujanju 

naziva Eulerovim brojem, a za dvije slične pojave vrijedi: 

p p′ 

= 

ρ ρ′ 

′ 

∞ ∞ 

2 2 

∞v∞ ∞v∞ ili Eu Eu′ 

∞ 

= gdje je 2 

ρ∞v∞ 

p sile tlaka 

Eu = = (K.3) 

inercijske sile 

Koeficijent u članu koji označuje viskozne sile u jednadžbi količine gibanja (C.2), definiran je 

Reynoldsovim brojem Re = ρvL / μ , te vrijedi: 

μ μ′ 

∞ ∞ = 

ρ vL ρ′ 

vL ′ ′ 

∞ ∞ ∞ ∞ 

1 1 

ili = 

Re Re′ 

gdje je 

ρ∞vL 

∞ inercijske sile 

Re = = (K.4) 

μ viskozne sile 

Općenito govoreći dva nestlačiva strujanja fluida će biti slična ako je zadovoljena jednakost 

Strouhalovih, Froudeovih, Eulerovih i Reynoldsovih brojeva prototipne i modelske pojave. Ako 

bi početni i rubni uvjeti bili zadani jednadžbama, iz njih bi se mogli pojaviti dodatni kriteriji 

sličnosti. U općem slučaju bezdimenzijsko polje tlaka i brzine u sustavu jednadžbi (C.1) i (C.2) 

zavisi od bezdimenzijskih prostornih i vremenske koordinate, te od koeficijenata koji se 

pojavljuju u jednadžbama, tj. vrijedi: 

p� = pxtStFrEuRe 

�( � i, 

�, 

, , , ) 

v� = v�( x� , t�, St, Fr, Eu, Re) 

i i i 

U zadanom primjeru nismo iskoristili definiciju za karakterističnu vrijednost vremena τ = L/ v∞. 

Ako se u definiciju (K.1) za Strouhalov broj uvrsti pretpostavljena relacija τ = L / v∞ 

, onda je 

jasno da će i u modelskoj i u prototipnoj pojavi vrijednost Strouhalova broja biti jednaka 

jedinici, što se može shvatiti da je jednakost Strouhalovih brojeva već zadovoljena, odnosno 

bezdimenzijska rješenja neće biti funkcija Strouhalova broja. Dakle nezavisni kriteriji sličnosti 

(oni o kojima rješenje problema ovisi) uvijek su definirani od veličina koje slijede iz 

konstanti koje se pojavljuju u jednadžbama (u ovom primjeru su to g , ρ∞ i μ∞ ) i konstanti 

iz početnih i rubnih uvjeta (ovdje su to L , p∞ i v∞ ), pa je jasno da se iz šest veličina, od kojih 

su tri dimenzionalno nezavisne, mogu definirati tri Π -parametra. Dakle u dvije pojave treba 

izabrati takve vrijednosti konstanti da bezdimenzijski koeficijenti (ovdje Fr , Eu i Re ) u dvije 

pojave budu jednaki, čime će se osigurati jednakost bezdimenzijskih rješenja. Za prototipnu 

pojavu, koju želimo ispitati na modelu, poznajemo vrijednosti svih šest utjecajnih veličina. U 

∞


modelskoj pojavi možemo izabrati slobodno tri od šest veličina, a preostale tri su definirane 

kriterijima sličnosti. Jedna od njih nam je već zadana jer se modelska pojava odvija u istom polju 

gravitacije ( g′ = g ), pa nam za slobodan izbor preostaju još dvije veličine. Ako je povod 

modelskim ispitivanjima smanjenje veličine objekta, onda biramo duljinu L′, a biramo i fluid u 

modelskoj pojavi, čime su određene ρ′ ∞ i μ′ ∞ , te smo već zadali četiri veličine, a možemo zadati 

samo tri. Ako smo zadali četiri veličine, s preostalim dvjema možemo zadovoljiti samo dva od 

tri kriterija sličnosti, što znači da ne bismo imali potpunu sličnost dvaju pojava. U praksi je to 

čest slučaj, a u takvim situacijama potrebno je izvršiti dopunsku analizu utjecaja pojedinih 

parametara na rješenje, tako da se zadovolji jednakost onih koeficijenata koji značajnije utječu 

na rezultat. Poslije ćemo analizirati utjecaj svakog od kriterija sličnosti, a sada pogledajmo 

alternativni način izvođenja kriterija sličnosti. 

Prema definiciji sličnosti veličine u dvije pojave povezane su koeficijentom sličnosti Cϕ u 

obliku ϕ = Cϕϕ′ , gdje je Cϕ jednako omjeru karakterističnih vrijednosti promatrane fizikalne 

veličine u dvije pojave Cϕ = Φ / Φ′ . Ako se u jednadžbama za prototipnu pojavu 

∂v 

∂x 

j 

j 

= 0 

∂vi ∂vi ∂p ∂ ⎛ ∂v 

⎞ 

i 

ρ∞ =−ρ∞vj −ρ∞gδi3− + μ∞ 

⎜ ⎟ 

∂t ∂xj ∂xi ∂x ⎜ 

j x ⎟ 

⎝∂ j ⎠ 

sve veličine izraze pomoću veličina modelske pojave, dobije se 

C ∂v′ 

v j 

= 0 

C ∂x′ 

L j 

(P.1) 

(P.2) 

2 

CC ρ v ∂v′ CC i ρ v ∂v′ C 

i p ∂p′ CC μ v ∂ ⎛ ∂v′ 

⎞ 

i 

ρ′ ∞ =− ρ′ v′ ∞ j − CC ρ g ρ′ g′ 

∞ δi3−+ μ′ 

2 ∞ ⎜ ⎟ 

Ct ∂t′ CL ∂x′ j CL 

∂x′ i CL ∂x′ ⎜ 

j ∂x′ 

⎟ 

⎝ j ⎠ 

U gornjim jednadžbama su plavom bojom označeni članovi koji čine jednadžbe modelske 

pojave. Svođenjem jednog od koeficijenata u gornjim jednadžbama na jedinicu dobije se 

∂v′ 

j 

= 0 

∂x′ 

j 

CL 

∂v′ i ∂v′ CC i L g Cp ∂p′ Cμ 

∂ ⎛ ∂v′ 

⎞ 

i 

ρ′ ∞ = −ρ′ v′ ∞ j − ρ′ g′ 

2 ∞ δi3− + μ′ 

2 

∞ ⎜ ⎟ 

CC v t ∂t′ ∂x′ j Cv CC ρ v ∂x′ i CCC ρ v L ∂x′ ⎜ 

j x′ 

⎟ 

⎝∂j⎠ Jasno je da će se iz prototipnih jednadžbi dobiti modelske jednadžbe, ako su svi koeficijenti 

jednaki jedinici, tj. vrijedi sljedeće: 

L 

CL 

= 1 ili L′ 

L L′ 

= 1 ili = ili St = St′ , što je jednako izrazu (K.1) 

CC v τ 

v t 

∞ v∞τv′ ∞τ′ 

v′ 

∞ τ ′ 

CC L g 

1 2 

C v 

= ili L g 

L′ g′ 

gL gL′ 

1 1 

= 1 ili = ili = što je jednako izrazu (K.2) 

2 

2 2 

2 2 

v∞ 

v∞ v′ 

∞ Fr Fr′ 

2 

v′ 

∞


p 

C p p′ 

= 1 ili 2 2 

CC ρ v ρ∞ 

v∞ 

2 

ρ′ 

∞ v′ 

∞ 

p p′ 

∞ ∞ 

= 1 ili = ili Eu = Eu′ što je jednako izrazu (K.3) 

2 2 

ρ∞v∞ ρ′ 

∞v′ ∞ 

μ∞ 

Cμ 

CCC ρ v L 

μ′ 

∞ 

= 1 ili = 1 ili 

ρ∞ 

v∞ L 

ρ′ 

∞ v′ ∞ L′ 

μ∞ ρ∞vL ∞ 

= 

μ′ 

∞ ili 

ρ′ 

∞vL ′ ′ ∞ 

1 

Re 

= 

1 

Re′ 

, vidjeti izraz (K.4) 

Dakle dobili smo iste kriterije sličnosti. Za one veličine koje se nalaze kao konstante u 

jednadžbama (u ovom primjeru su to g , ρ∞ i μ∞ ) ili su zadane početnim i rubnim uvjetima 

(ovdje su to L , p ∞ i v ∞ ) (dakle parametre koje zadajemo) možemo definirati nezavisne 

koeficijente sličnosti. Dakle, jasno je da će koeficijent sličnosti za vrijeme (za kojeg nemamo 

parametra kojim bi unaprijed definirali pripadajući koeficijent sličnosti) biti definiran kriterijem 

(K.1) iz kojega je Ct = CL / Cv, 

odnosno Strouhalov broj je iskorišten za definiciju koeficijenta 

sličnosti za vrijeme, pa on nije kriterij sličnosti dvaju strujanja. U ovoj pojavi je C g = 1, 

a nakon 

izbora mjerila modela (koeficijenta sličnosti C L za duljinu) i fluida u modelskoj pojavi 

(definirani Cρ i Cμ ) možemo još odrediti koeficijente sličnosti p C i C v tako da zadovoljimo 

dva od preostala tri kriterija sličnosti. Kao što je već rečeno u situaciji u kojoj ne možemo 

zadovoljiti sve kriterije sličnosti, jer smo prisiljeni zadati veći broj veličina nego imamo 

dimenzionalno nezavisnih veličina, potrebno je zadovoljiti najutjecajnije kriterije sličnosti. 

Analiza važnosti bezdimenzijskih parametara 

Strouhalov broj 

Strouhalov broj se nalazi na mjestu koeficijenta uz član koji označuje lokalnu promjenu odnosno 

nestacionarnost strujanja, te se odmah zaključuje da će biti bitan samo u nestacionarnom 

strujanju. Nestacionarnost strujanja može biti posljedica vremenski promjenjivih rubnih uvjeta, 

kada je na temelju vremenske promjene rubnih uvjeta moguće definirati karakteristično vrijeme. 

Ako bi npr. tijelo, na koje nastrujava fluid konstantnim i jednolikim profilom brzine vibriralo 

određenom frekvencijom ω, tada bi strujanje bilo nestacionarno, a karakteristično vrijeme bi se 

moglo definirati periodom tih vibracija τ=1/ω, odnosno Strouhalov broj bi bio: 

St 

∞ 

L ω L 

= = 

v τ v 

∞ 

∞ 

Nasuprot nestacionarnom strujanju s vremenski promjenjivim rubnim uvjetima, postoje i 

nestacionarna strujanja s vremenski konstantnim rubnim uvjetima. Na primjer ako je zatvoreni 

prostor pregrađen membranom, tako da se sa svake strane membrane nalazi plin pod različitim 

tlakom, nakon trenutnog puknuća membrane doći će do nestacionarnog strujanja plina, uz 

stacionarne rubne uvjete. Drugi tipični primjer nestacionarnog strujanja uz stacionarne rubne 

uvjete je nestlačivo optjecanje valjka jednolikim i konstantnim profilom brzine, gdje na 

stražnjem dijelu površine valjka, dolazi do odvajanja strujanja i periodičkog otkidanja vrtloga. U 

takvim se slučajevima karakteristično vrijeme ne može definirati na temelju vremenske 

promjene rubnih uvjeta, nego se ono definira s pomoću raspoloživih karakterističnih veličina, 

npr. karakteristične brzine i karakteristične duljine u obliku τ = L/ v∞. 

U tom je slučaju 

Strouhalov broj identički jednak jedinici u obje pojave, što drugim riječima znači da je kriterij 

Strouhalova broja automatski zadovoljen. Budući da je rješenje nestacionarno, moguće je


definirati neko karakteristično vrijeme koje karakterizira vremensku promjenu rješenja, ali to 

vrijeme ne predstavlja osnovu za postavljanje kriterija sličnosti, jer je ono svojstvo samog 

rješenja, a ne dolazi iz rubnih uvjeta. Tako bi se u problemu optjecanja valjka jednolikim i 

konstantnim profilom brzine, mogao definirati Strouhalov broj na temelju frekvencije otkidanja 

vrtloga, koji bi bio definiran analogno izrazu (K.1), ali taj Strouhalov broj, kao što je rečeno ne 

bi označavao nezavisni kriterij sličnosti (čijim bi podešavanjem uvjetovali rješenje) jer on sam 

dolazi iz rješenja. 

Dakle, Strouhalov broj će se pojavljivati kao nezavisni kriterij sličnosti samo u 

problemima s vremenski promjenjivim rubnim uvjetima. 

Froudeov broj 

Froudeov broj označuje odnos inercijske i gravitacijske sile. Ovaj će broj biti značajan u opisu 

problema kod kojih je bitan utjecaj gravitacije na polje brzine, odnosno kod kojih je bitna 

preraspodjela potencijalne i kinetičke energije. Tipični primjer pojave u kojoj je Froudeov broj 

nezaobilazan kriterij sličnosti su površinski valovi nastali gibanjem broda po površini vode, kod 

kojih upravo dolazi do preraspodjele između kinetičke i potencijalne energije čestica fluida (jer 

je tlak na slobodnoj površini konstantan). Pri istjecanju fluida iz velikog spremnika, također 

dolazi do pretvorbe potencijalne energije u kinetičku, te će sila gravitacije biti značajna za polje 

brzine. Nasuprot tome, ako se promatra strujanje kroz kosu cijev konstantnog poprečnog 

presjeka između dva presjeka sa zadanim tlakom, iz Bernoullijeve jednadžbe i jednadžbe 

kontinuiteta je jasno da gravitacijska potencijalna energija nema utjecaja na polje brzine (jer 

kinetička energija ne zavisi od potencijalne energije), a sila gravitacije utječe samo na polje 

tlaka. Slično se može zaključiti i za slučaj horizontalnog optjecanja tijela potopljenog duboko 

ispod slobodne površine (tako da se na slobodnoj površini ne pojavljuju valovi). Ako se od 

stvarnog polja tlaka oduzme promjene tlaka nastala uslijed gravitacije, slika strujanja se neće 

promijeniti, iz čega se zaključuje da masene sile nemaju utjecaja, odnosno Froudeov broj nije 

kriterij sličnosti. Iz sličnih se razloga pri strujanju plinova s nametnutim gradijentom tlaka u 

smjeru strujanja (slučaj prisilne konvekcije), utjecaj gravitacije redovito zanemaruje. 

Eulerov broj, kavitacijski broj, Machov broj 

U nestlačivom strujanju razina tlaka nema utjecaja na polje strujanja, jer tlak nema utjecaja na 

gustoću fluida, a njegov utjecaj na polje brzine se očituje kroz gradijent tlaka, koji se pojavljuje 

u jednadžbi količine gibanja. Jasno je da se polju tlaka može dodati konstanta a da se polje 

brzine ne promijeni. Ako su u nekom problemu zadane brzine po rubu područja, tlak se zadaje 

samo u jednoj točki, pa je jasno da u takvim uvjetima Eulerov broj nije nezavisni kriterij 

sličnosti, jer polju tlaka možemo dodati ili oduzeti konstantnu vrijednost bez da se slika strujanja 

promijeni (dakle Eulerov broj se može smatrati zadovoljenim). U takvim se slučajevima za 

karakterističnu vrijednost tlaka bira dvostruka vrijednost dinamičkog tlaka, pa je Eulerov broj 

jednak jedinici, što znači da ispada iz skupa nezavisnih parametara. 

Jednakost Eulerova broja će morati biti zadovoljena u dva strujanja u kojima je zadana neka 

razlika tlaka, čime je na neki način određen gradijent tlaka. Na primjer u pojavi strujanja kroz 

cijev, ako je tlak zadan na ulaznom i izlaznom presjeku cijevi, razlika tih tlakova postaje 

presudna za vrijednost brzine strujanja. U tom slučaju se Eulerov broj može definirati izrazom u 

kojem se tlak zamjenjuje razlikom tlaka 

Δ p 

Eu = 2 

ρ∞v∞ Slično vrijedi i kod pumpe, koja predaje energiju fluidu, pa se tlak od ulaza do izlaza iz pumpe 

poveća za Δ p .


Sljedeći primjer, gdje je zadana razlika tlaka su pojave nestlačivog strujanja s mogućnošću 

pojave kavitacije, kada je zadan tlak p v para, pa je Δ p = p∞− pv. 

Dakle ako se u jednom 

strujanju pojavljuje kavitacija, treba osigurati uvjete za pojavu kavitacije i u njemu sličnom 

strujanju. Za te se potrebe Eulerov broj preuređuje u kavitacijski broj, koji je definiran izrazom 

p∞−pv σ = 2 

ρ∞v∞ 

U analizi stlačivih strujanja, kod kojih se gustoća fluida značajno mijenja, Eulerov broj se može 

prevesti u Machov broj, koji je u stlačivom strujanju važan kriterij sličnosti. Znamo da je sila 

tlaka na česticu fluida odgovorna za promjenu njena volumena, odnosno gustoće, pa se govori o 

sili tlaka kao o sili stlačivanja. U savršenom plinu je brzina zvuka definirana izrazom 

2 

c = κp/ ρ (κ je eksponent adijabatske ekspanzije), pa se Eulerov broj može zapisati u obliku 

2 

p∞ κ 1 c∞ 

1 1 

v inercijske sile 

Eu = = = , gdje je Ma = = . 

2 2 2 

ρ∞v∞κ κ v∞κ Ma 

c sile stlačivanja 

Strujanje plinova pri niskim vrijednostima Machova broja (recimo Ma < 0.3) 

tretiramo kao 

nestlačivo strujanje, jer je promjena gustoće u takvim strujanjima s inženjerskog stajališta 

zanemariva. Tako se npr. strujanje zraka oko automobila, koji se kreće brzinom recimo 150 km/h 

(41.7 m/s), pri brzini zvuka, koja pri normalnim uvjetima zraka iznosi 331 m/s, odvija pri 

Machovom broju Ma = v / c = 0.125, 

pa se redovito smatra nestlačivim. Kod modelskih 

ispitivanja istog problema treba paziti da u sličnoj pojavi Machov broj ne prijeđe, recimo 

vrijednost 0.3, jer bi tada u modelskoj pojavi strujanje bilo sa značajnim utjecajem sila 

stlačivanja, nego u originalnoj pojavi, pa bi sličnost strujanja bila narušena. 

Reynoldsov broj 

Jedan od najvažnijih bezdimenzijskih parametara, bilo za slučaj vanjskih zadaća (optjecanja) 

bilo unutarnjih zadaća (protjecanja fluida) je upravo Reynoldsov broj. Kao što je jasno iz 

jednadžbe količine gibanja on označuje omjer inercijskih i viskoznih sila i glavni je kriterij 

prelaska laminarnoga u turbulentno strujanje fluida. Laminarno strujanje fluida održava se pri 

malim vrijednostima Reynolsova broja, gdje je utjecaj viskoznosti veći. Velike vrijednosti 

Reynoldsova broja označuju mali utjecaj viskoznosti, te se pri visokim vrijednostima 

Reynolsova broja viskozne sile mogu i zanemariti u većem dijelu područja strujanja. Međutim, 

kad god u području strujanja postoji čvrsta stijenka utjecaj viskoznih sila se neće moći 

zanemariti u neposrednoj blizini stijenke. Zbog viskoznosti fluida brzina fluida na stijenci 

jednaka je nuli, a udaljavanjem od stijenke brzina čestica fluida se postupno povećava. Zbog 

toga će uz stijenku uvijek postojati područje u kojem se strujanje fluida odvija malim brzinama s 

malim inercijskim silama, te se u tom području (koje se naziva graničnim slojem) utjecaj 

viskoznih sila neće moći zanemariti. U tim će slučajevima Reynoldsov broj biti važan kriterij 

sličnosti. Postoje viskozna strujanja fluida u kojima Reynoldsov broj nije nezavisni kriterij 

sličnosti. Jedno takvo je npr. problem prirodne konvekcije (strujanje koje nastaje uslijed izmjene 

topline, tj. razlike u gustoći koja nastaje zbog razlike temperatura čestica fluida) u zatvorenom 

prostoru, gdje su brzine po svim granicama jednake nuli, te iz rubnih uvjeta nije moguće 

definirati karakterističnu brzinu, koja bi ušla u definiciju Reynoldsova broja. Naravno, u takvom 

bi se strujanju mogao definirati Reynoldsov broj na temelju npr. maksimalne brzine koja se 

pojavljuje u rješenju. U sličnim strujanjima bi vrijedila jednakost tako definiranog Reynoldsova 

broja u dvije pojave, a s obzirom da je Reynoldsob broj definiran na temelju brzine koja dolazi iz 

rješenja, on ne bi označavao nezavisni kriterij sličnosti.


KLASIFIKACIJA STRUJANJA FLUIDA 

Treba naglasiti da se prije izvedene Navier-Stokesove jednadžbe odnose na strujanje 

newtonskog, jedno-komponentnog jednofaznog fluida (dakle bez kemijske reakcije) i bez 

utjecaja elektro-magnetskih sila. 

Jasno je da se u praksi pojavljuju i višekomponentna strujanja, npr. pri miješanju dvaju (ili 

više) plinova. U takvim situacijama bi se kao nove varijable pojavile koncentracije svakog 

pojedinog plina, te novi članovi koji označuju masenu difuziju pojedinih komponenti. Treba 

naglasiti da je i zrak smjesa plinova, ali je koncentracija svake sastavnice zraka konstantna i 

jednaka u svim točkama fluida (dakle nema difuzije mase), pa se zrak tretira kao jednokomponentni 

fluid. 

Ako se u strujanju istovremeno pojavljuje više agregatnih stanja (kruto, kapljevito i 

plinovito), strujanje se naziva višefaznim. Pri pojavi kavitacije strujanje vode postaje 

dvofazno, jer se osim kapljevite faze pojavljuje i plinovita faza. U tom se slučaju pojavljuje 

razdjelna površina između dvaju faza u kojoj se pojavljuju dodatne sile površinske napetosti, 

a u takvom strujanju bi također trebalo definirati brzinu pretvorbe kapljevite u plinovitu fazu, 

i obrnuto. Tipičan primjer višefaznog strujanja je i strujanje u kotlovskim cijevima, u kojima 

voda isparava zbog dovođenja topline. Dakako da postoje i višekomponentna višefazna 

strujanja. Primjer za to je pneumatski transport krutih čestica (strujanje mješavine zraka i 

krutih čestica). 

Ako se ograničimo samo na Navier-Stokesove jednadžbe, još uvijek možemo razlikovati 

nekoliko podjela strujanja. 

Jedna od podjela koju smo već do sada spominjali je s obzirom na gustoću. Ako gustoća 

ostaje konstantna u strujanju, strujanje zovemo nestlačivim, inače je stlačivo. Treba naglasiti 

da je pojam stlačivosti bolje vezati uz strujanje, jer se i strujanje plinova (kao izrazito stlačivih 

fluida) pri niskim vrijednostima Machova broja može smatrati nestlačivim, a strujanje vode 

(kao izrazito nestlačivog fluida) se tretira stlačivim za slučaj pojave enormne razlike tlakova 

(npr. za slučaj podvodne eksplozije). 

Strujanje u kojem nema izmjene topline među česticama fluida se naziva adijabatskim, a u 

protivnom je strujanje dijabatsko. Za dijabatsko strujanje u kojem temperatura ostaje 

konstantna u svim točkama fluida se kaže da je izotermičko. 

S obzirom na viskoznost strujanje može biti neviskozno (viskoznost je jednaka nuli) ili 

viskozno. Jednadžbe gibanja neviskoznog strujanja se dobiju iz Navier-Stokesovih jednadžbi 

u kojima se viskoznost izjednači s nulom, a takve se jednadžbe nazivaju Eulerovim 

jednadžbama. Posebnu klasu neviskoznog strujanja čine potencijalna strujanja, u kojima se 

dodatno pretpostavlja da nema rotacije čestica fluida, što ima za posljedicu da se polje brzine 

može prikazati gradijentom skalarne funkcije (skalarnog potencijala brzine). Dakle 

neviskozno strujanje je općenito opisano Eulerovim jednadžbama koje su nelinearne (zbog 

nelinearnog inercijskog člana u jednadžbi količine gibanja). Uz pretpostavku potencijalnog 

nestlačivog strujanja linearna jednadžba kontinuiteta prelazi u linearnu Laplaceovu 

jednadžbu, a nelinearna parcijalna diferencijalna jednadžba količine gibanja prelazi u 

nelinearnu algebarsku jednadžbu (Euler-Bernoullijev integral), pa je potencijalno strujanje 

puno jednostavnije riješiti od općenitog neviskoznog strujanja opisanog nelinearnim 

Eulerovim jednadžbama. Viskozno strujanje u prirodi se pojavljuje kao laminarno ili 

turbulentno. Laminarno strujanje je uredno strujanje u kojem se čestice fluida gibaju u 

slojevima (po glatkim trajektorijama), za razliku od turbulentnog strujanja u kojem se


pojavljuju slučajne pulzacije brzine, tako da su čestice fluida u stanju burnog komešanja. U 

prirodi se laminarno strujanje održava pri niskim vrijednostima Reynoldsova broja (pri 

značajnijem utjecaju viskoznih sila). U praksi su strujanja najčešće turbulentna, a zbog 

njihove stohastičke prirode, turbulentna strujanja fluida se ne mogu opisati analitički pa ih se 

nužno rješava numeričkim putem. 

Naravno da se na temelju nabrojanih podjela mogu definirati različite klase strujanja fluida, 

npr. nestlačivo, izotermičko laminarno; ili stlačivo, adijabatsko potencijalno, i sl. 

S obzirom na rubne uvjete strujanja se dijele na vanjska (problemi optjecanja tijela – jedan od 

rubova je stijenka) i unutarnja (problemi protjecanja, npr. kroz kanale i cijevi – dva ruba 

područja strujanja su stijenke). 

OPTJECANJE TIJELA – TEORIJA GRANIČNOG SLOJA 

Jedna od tipičnih zadaća mehanike fluida je određivanje sile koja djeluje na gibajuće tijelo 

uronjeno u fluid. Tipični primjeri su gibanje automobila, vlaka, zrakoplova, broda, rotora 

turbostroja itd. Za slučaj gibanja tijela konstantnom brzinom, problem se obično promatra u 

koordinatnom sustavu vezanom na tijelo, te bi se promatraču u tom koordinatnom sustavu 

činilo da tijelo miruje, a fluid nastrujava na njega brzinom koja je jednaka brzini gibanja 

tijela. 

Primjer ravninskog strujanja. 

ρ, v ∞ 

S 

Rezultantna sila fluida na tijelo jednaka je integralu površinskih sila po površini tijela. 

∫ ∫ ∫ 

F = σ ⋅ n dS =− p⋅ ndS+ Σ n dS 

i ji j i ji j 

S S S 

Gdje je −∫ p ⋅nidS 

doprinos sila tlaka, a ∫ Σ jinjdS doprinos viskoznih sila. 

S 

S 

L 

Sila fluida na tijelo obično se za slučaj ravninskog strujanja rastavlja na dvije komponente. 

� 

Komponenta D (ili F D ) u smjeru brzine v∞ (označuje silu otpora, prema engl. "Drag") i 

komponentu L ili ( L F ) okomito na brzinu v � 

∞ (označuje silu uzgona, prema engl. "Lift"). 

F i 

D


Sile otpora i uzgona se najčešće prikazuju u bezdimenzijskim oblicima koeficijenta otpora i 

koeficijenta uzgona, koji su definirani izrazima 

D 

L 

CD 

= 

i CL 

= 

1 2 

1 2 

ρ ⋅v∞⋅AD ρ ⋅v∞⋅AL 2 

2 

1 2 

gdje je ρ ⋅ v∞ 

dinamički tlak, a A D i A L površine. 

2 

Površine D A i A L se mogu definirati različito, a kod sile otpora je to najčešće projekcija 

površine tijela suprotstavljena strujanju. U "Mehanici Fluida I" su dani koeficijenti otpora 

nekih elementarnih tijela, dobiveni mjerenjem. U općem slučaju koeficijent otpora zadanog 

tijela, u nestlačivom strujanju zavisi od Reynoldsova broja, a u stlačivom od Reynoldsova i 

Machova broja. 

Doprinos sili otpora od tlačnih sila se naziva otpor oblika, a od viskoznih sila otpor trenja. 

Slijedeće dvije slike prikazuju dva ekstremna slučaja optjecanja tanke ploče. 

p 

100 % otpor trenja. 100 % otpor oblika. 

v ∞ 

x 2 

p 

σ21= τw 

x 1 

v ∞ 

σ12= τw 

U prvom su slučaju sile tlaka okomite na smjer strujanja, pa sili otpora doprinose samo 

viskozne sile, a u drugom slučaju je obrnut slučaj, smične sile su okomite na smjer strujanja, 

pa sili otpora doprinose samo tlačne sile. U realnim slučajevima uvijek imamo i jedan i drugi 

doprinos otporu. 

Primjer ravninskog strujanja. 

v ∞ 

α 

Ako se kao primjer uzme ravninsko optjecanje profila, onda će otpor oblika rasti s debljinom 

profila i s porastom napadnog kuta α. 

p 

τ 

p 

x 2 

x 1


Polje brzine pri optjecanju tijela zavisi od inercijskih sila, sila tlaka i viskoznih sila (utjecaj 

masenih sila se obično zanemaruje). Odnos inercijskih i viskoznih sila je prikazan 

Reynoldsovim brojem, pri čemu niske vrijednosti Reynoldsova broja označuju zanemariv 

utjecaj inercijskih sila (odnosno značajan utjecaj viskoznih sila). U takvim slučajevima se 

inercijske sile (nelinearni konvekcijski član u jednadžbi količine gibanja) mogu zanemariti, 

čime se od Navier-Stokesovih jednadžbi dobiju Stokesove jednadžbe. Stokesove jednadžbe su 

linearne pa se može naći analitičko rješenje npr. optjecanja kugle, koje vrijedi za slučaj 

Re � 1. 

Primjer strujanja kojeg opisuju Stokesove jednadžbe je i strujanje ulja u zračnosti 

ležaja (vidjeti primjer s vježbi, gdje su inercijske sile zanemarene na temelju procjene reda 

veličine pojedinih članova u jednadžbi količine gibanja). Drugi primjer primjene Stokesovih 

jednadžbi je ulijevanje npr. polimera u kalup. U takvim problemima viskoznost je obično 

velika, a brzine relativno male, pa je Reynoldsov broj mali. Međutim polimer najčešće nije 

newtonski fluid pa se koristi neka druga relacija za zavisnost tenzora viskoznih sila od tenzora 

brzine deformacije. 

U praktičnim problemima optjecanja tijela (strujanje oko zrakoplova, automobila, vlaka ili 

broda) Reynoldsov broj poprima vrijednosti puno veće od jedinice, što znači da je utjecaj 

viskoznih sila mali. Ipak viskozne sile se neće moći zanemariti u čitavom području strujanja, 

nego je samo njihov utjecaj sveden na područje u neposrednoj blizini tijela, u kojem će se 

brzina fluida mijenjati od nule (na samoj površini tijela) do brzine optjecanja. To područje se 

naziva područje graničnog sloja. Dakle pri optjecanju tijela pri visokim vrijednostima 

Reynoldsova broja, viskozne sile su bitne samo unutar tankog graničnog sloja, a izvan 

graničnog sloja utjecaj viskoznosti se može zanemariti. 

Sljedeća slika shematski prikazuje primjer graničnog sloja uz ravnu ploču pri visokoj 

ρvL 

∞ 

vrijednosti Reynoldsova broja Re = (L je duljina ploče). Debljina graničnog sloja 

μ 

(osjenčanog područja unutar kojeg se brzina znatno mijenja, odnosno područja u kojem su 

viskozne sile bitne) je mala u odnosu na duljinu ploče. 

Veliki Re 

v ∞ 

y 

ρ, μ = konst. 

područje vanjskog 

strujanja 

mali gradijent brzine 

= 

zanemariv utjecaj viskoznosti 

područje graničnog sloja 

= 

veliki utjec aj viskoznosti zb og 

velikog gradijenta brzine 

Međutim, ako promatramo strujanje u okolišu samog vrha ploče (ili imamo posla s kratkom 

pločom, tako da je Reynoldsov broj mali (što odgovara velikom utjecaju viskoznosti), 

debljina područja unutar kojeg će viskozne sile biti značajne u odnosu na inercijske sile će biti 

velika u odnosu na duljinu ploče, kao što shematski prikazuje sljedeća slika. Ako se 

Reynoldsov broj općenito definira kao Re= ρv∞x/ μ , gdje je x udaljenost od vrha (prednjeg 

brida) ploče, odmah je jasno da će veći utjecaj viskoznosti biti bliže vrhu, gdje je Reynoldsov 

broj manji. 

x


Mali Re (promatramo vrh ploče) 

v ∞ 

ρ, μ= 

konst. 

utjecaj viskoznosti je 

značajan u okolini vrha 

Slično se da zaključiti i iz primjera optjecanja kugle promjera D . Za optjecanje pri niskim 

ρvD 

∞ 

vrijednostima Reynoldsova broja Re = , recimo Re � 1, 

postoji analitičko rješenje, po 

μ 

kojemu se utjecaj viskoznosti u polju brzine osjeti daleko od tijela (prva slika), a za slučaj 

Mali Re 

v ∞ 

v ∞ 

utjecaj viskoznosti 

se širi daleko od kugle 

Veliki Re 

granični sloj 

zona utjec a ja viskoznosti 

vrtložni trag 

Neviskozno strujanje bilo bi i bezvrtložno 

(Lapla c e-o va jednadžba 

)


visokih vrijednosti Reynoldsova broja, utjecaj viskoznosti na polje brzine, sveden je u usko 

područje graničnog sloja uz samu površinu kugle. Što god je Reynoldsov broj veći to je 

područje relativno tanje. 

Temeljem rečenoga sama od sebe se nameće Prandtlova ideja, da se za slučaj optjecanja tijela 

pri visokim vrijednostima Reynoldsova broja, polje strujanja rastavi na dva područja: 

Područje neposredno uz površinu tijela (granični sloj) gdje je utjecaj viskoznosti bitan i 

vanjsko neviskozno strujanje opisano Eulerovim jednadžbama (odnosno uz dodatnu 

pretpostavku bezvrtložnog strujanja, nelinearne Eulerove jednadžbe prelaze u linearnu 

Laplaceovu jednadžbu i algebarsku Bernoullijevu jednadžbu - točnije Euler-Bernoullijev 

integral). 

Strujanje unutar graničnog sloja je viskozno, što znači da je opisano Navier-Stokesovim 

jednadžbama. Međutim, činjenica da je granični sloj tanak u odnosu na duljinu tijela, ima za 

posljedicu da svi članovi u Navier-Stokesovim jednadžbama neće biti jednako veliki. 

Procjenom reda veličine pojedinih članova u tim jednadžbama i zanemarivanjem članova koji 

malo doprinose rješenju dolazi se do skupa pojednostavljenih jednadžbi koje opisuju strujanje 

fluida unutar graničnog sloja, a koje se nazivaju Prandtlovim jednadžbama. 

Prandtlove jednadžbe za granični sloj 

Pri izvodu Prandtlovih jednadžbi ograničit ćemo se na ravninsko strujanje oko blago 

zakrivljene stjenke (što pretpostavlja da je polumjer zakrivljenosti stijenke puno veći od 

debljine graničnog sloja). Nadalje uvode se sljedeće pretpostavke 

- Strujanje je nestlačivo uz konstantnu viskoznost ( ρ = konst. , μ = konst. ) 

∂ 

- Strujanje je stacionarno: = 0 

∂t 

- Zanemarujemo masene sile: f i = 0 

y 

y 


R> > debljina graničnog sloja 

Strujanje se promatra u 0xy koordinatnom sustavu, gdje se os x poklapa s konturom 

površine tijela (stijenke), a os y je u svakoj točki okomita na os x (stijenku). Komponentu 

brzine u smjeru osi x , označit ćemo s u , a komponentu u smjeru osi y s v . 

x


Polazne jednadžbe su jednadžba kontinuiteta (JK) i jednadžbe količine gibanja (JKG), koje uz 

navedene pretpostavke glase 

∂u ∂v 

JK + = 0 

∂x ∂y 

JKG – x - komponenta 

2 2 

∂u ∂u 1 ∂p ⎛∂ u ∂ u⎞ 

u + v =− + υ ⎜ + 2 2 ⎟ 

∂x∂y ρ ∂x ⎝∂x ∂y 

⎠ 

2 2 

∂v ∂v 1 ∂p ⎛∂ v ∂ v⎞ 

JKG – y - komponenta u + v =− + υ ⎜ + 2 2 ⎟ 

∂x∂y ρ ∂y ⎝∂x ∂y 

⎠ 

U cilju procjene veličine pojedinih članova u jednadžbi, uvodimo karakteristične veličine za 

pojedine varijable u obliku 

u = Uu� 

v = Vv� 

x = Lx� 

y = δ y� 

2 

S obzirom da je strujanje nestlačivo za tlak se uzima p = ρU 

p� 

(pretpostavimo da je red 

veličine maksimalne promjene tlaka unutar graničnog sloja jednak dvostrukom dinamičkom 

tlaku). 

Gdje su U i V maksimalne brzine u pojedinim smjerovima, tako da su vrijednosti 

bezdimenzijskih komponenti u� i v� brzine u rasponu nula do jedan (kažemo da su 

bezdimenzijske komponente brzine reda veličine jedan). S obzirom da su duljina L i debljina 

graničnog sloja δ maksimalne dimenzije u smjeru osi x i y , jasno je da su i bezdimenzijske 

koordinate x� i y� također reda veličine jedinice (jer se kreću u rasponu nula do jedan). 

Uvrštavanjem gornjih relacija u jednadžbu kontinuiteta, ona prelazi u oblik 

U ∂u V ∂v 

⋅ + ⋅ 0 

L ∂xδ∂ y 

= 

� � 

� � 

Bezdimenzijski članovi u jednadžbi kontinuiteta su reda veličine jedinice (jer je maksimalna 

promjena komponenti reda veličine jedinice, a maksimalna promjena bezdimenzijske 

koordinate je također reda veličine jedinice). S obzirom da zbroj članova u gornjoj jednadžbi 

mora biti jednak nuli, zaključujemo da su koeficijenti uz članove istog reda veličine, tj. vrijedi 

U V 

δ 

= , odakle je V = U (a) 

L δ 

L 

Jasno da je za slučaj strujanja pri visokim vrijednostima Reynoldsova broja, kako je prije 

objašnjeno, debljina graničnog sloja puno manja od duljine L , pa je i maksimalna vrijednost 

v -komponente brzine puno manja od maksimalne vrijednosti u -komponente, što znači da je 

strujanje u graničnom sloju uglavnom paralelno sa stijenkom. 

Prikazom x -komponente jednadžbe količine gibanja s pomoću bezdimenzijskih veličina 

dobije se


U ∂ UV ∂ U ∂ ∂ U ∂ 

⋅ u + ⋅ v⋅=− 

⋅ + υ ⋅ + υ 

L ∂xδ ∂yρL∂x L ∂x δ ∂y 

⋅ 

� � � � � 

� � 

� � � � � 

2 2 

2 2 

u u ρ p U u u 

2 2 2 2 

� �� 

2 

U U U 

� 

L 2 2 

L 

υ υ δ 

Ponovo su bezdimenzijski članovi reda veličine jedinice, a većina koeficijenata je reda 

veličine 

2 

U 

L 

. S obzirom da je δ � L predzadnji član gornje jednadžbe je zanemariv u odnosu 

U 

na zadnji član, pa ostaje da je red veličine viskoznih sila υ . Da bi viskozne sile bile 

2 

δ 

značajne unutar graničnog sloja, moraju biti istog reda veličine kao i inercijske sile, tj. vrijedi 

2 

2 

U U 

⎛δ ⎞ υ 1 

= υ tj. vrijedi 

2 

⎜ ⎟ = = , odnosno 

L δ 

⎝L⎠ UL Re 

L L 

δ = = (b) 

UL Re 

υ 

6 

Dakle, ako je Reynoldsov broj reda veličine 10 onda je debljina graničnog sloja tri reda 

veličine manja od duljine L . Ako se x -komponenta jednadžbe količine gibanja podijeli s 

2 

U / L, dobije se 

2 2 

∂u� ∂u� ∂p� 1 ∂ u� 

∂ u� 

u� + v�⋅ 

=− + ⋅ + 2 2 

∂x� ∂y� ∂x� Re 

∂x� 

∂y� 

u kojoj je predzadnji član očito zanemariv, za slučaj strujanja pri visokim vrijednostima 

Reynoldsova broja. 

Konačno prikazom y -komponente jednadžbe količine gibanja s pomoću bezdimenzijskih 

članova, uvažavajući relacije (a) i (b) dobije se 

2 2 

2 2 

UV ∂v� V ∂v� ρU 

∂p� V ∂ v� V ∂ v� 

⋅ u� + ⋅ v� 

=− ⋅ + υ ⋅ + υ ⋅ 

2 2 2 2 

�L ∂x� �δ ∂y� � 

ρδ ∂y� �L ∂x� 

�δ 

∂y� 

2 2 

2 

2 

2 

U U U U 

U 

3 

L Re 

Re 

L Re L LRe ⋅ 2 

L Re 

Dijeljenjem gornje jednadžbe koeficijentom uz derivaciju tlaka sijedi 

2 2 

1 ⎛ ∂v ∂v⎞ ∂p 

1 ∂ v 1 ∂ v 

⋅⎜u⋅ + v ⎟= 

− + ⋅ + ⋅ 

2 2 2 

Re ⎝ ∂x∂y⎠∂y Re ∂xRe ∂y 

� 

� � � � 

� � 

� � � � � 

Očito su svi članovi ove jednadžbe za slučaj strujanja pri visokim vrijednostima Reynoldsova 

broja zanemarivi, te od polaznog sustava ostaju sljedeće bezdimenzijske Prandtlove jednadžbe 

∂u� ∂v� 

JK + = 0 

∂x� ∂y� 

JKG – x - komponenta 

∂ p� 

JKG – y - komponenta = 0 

∂y� 

2 

∂u� ∂u� ∂p� ∂ u� 

u� + v� 

=− + 2 

∂x� ∂y� ∂x� ∂y�


Rekapitulacija modela graničnog sloja 

Sljedeća slika prikazuje dio područja strujanja pri optjecanju nekog dijela, koje smo podijelili 

na područje graničnog sloja ( 0 < y < δ ( x) 

) i područje vanjskog neviskoznog strujanja 

( y > δ ( x) 

). Brzinu na granici između ta dva područja (na rubu graničnog sloja) smo označili s 

vδ . Pretpostavlja se da se profil brzine u graničnom sloju glatko nastavlja na profil brzine u 

∂vδ 

vanjskom neviskoznom strujanju, tako da vrijedi = 0 , tj. zaključujemo da će u 

∂y 

v = v x . 

ravninskom stacionarnom strujanju brzina v δ biti funkcija samo koordinate x , tj. ( ) 

y 

v δ 

y ∞ 

δ(x) 

x 

δ δ 


Strujanje fluida unutar graničnog sloja je opisano Prandtlovim jednadžbama, koje za slučaj 

stacionarnog, ravninskog strujanja, u dimenzijskom obliku glase 

∂u ∂v 

+ = 0 

∂x ∂y 

2 

∂u ∂u 1 ∂p ∂ u 

u + v =− + υ 2 

∂x∂y ρ ∂x ∂y 

∂ p 

= 0 

∂y 

Iz treće jednadžbe se zaključuje da je tlak po presjeku graničnog sloja konstantan, odnosno da 

je u stacionarnom ravninskom strujanju tlak funkcija samo koordinate x , tj. p = p( x) 

. Dakle 

ostaju nam prve dvije jednadžbe u kojima su tri nepoznata polja: u , v i p , pa je jasno da se 

Prandtlove jednadžbe ne mogu riješiti neovisno o vanjskom neviskoznom strujanju, koje je 

opisano Eulerovim jednadžbama (odnosno ako se može pretpostaviti bezvrtložno strujanje 

Laplaceovom jednadžbom). Za brzinu vδ na rubu graničnog sloja, uzimajući da vrijedi 

( ) 

v = v x , iz Eulerove jednadžbe za stacionarno ravninsko strujanje vrijedi 

δ δ 

dvδ1 dp 

vδ 

=− 

dxρdx Na taj način je usklađen broj jednadžbi i broj nepoznatih polja, a jednoznačno rješenje je 

definirano zadavanjem rubnih uvjeta. Prandtlove jednadžbe su paraboličkog tipa, pa je 

potrebno zadati sljedeće rubne uvjete 

1) na ploči: za y = 0; 

u = v= 

0 (viskozni fluid se lijepi na stijenku) 

2) dovoljno daleko od tijela: za y →∞; u = u ; v= v (ne osjeća se utjecaj tijela) 

∞ ∞ 

3) ulazni presjek: na x = 0 ; zadati profile komponenti brzine u i v.


Pri optjecanju tijela, se na prednjoj strani pojavljuje točka zastoja u kojoj se strujanje račva na 

dvije strane. Kao što je prije rečeno u okolišu točke zastoja je brzina mala, pa Reynoldsov 

broj poprima niske vrijednosti, što znači da u okolišu točke zastoja Prandtlove jednadžbe 

(koje su izvedene uz pretpostavku visokih vrijednosti Reynoldsova broja) ne vrijede. Stoga 

presjek x = 0 od kojeg se počinju integrirati Prandtlove jednadžbe treba odabrati dovoljno 

daleko od točke zastoja, gdje je Reynoldsov broj dovoljno velik. 

Valja primijetiti da su Prandtlove jednadžbe također nelinearne parcijalne diferencijalne 

jednadžbe, za koje ne poznamo opće analitičko rješenje, te će ih se trebati rješavati 

numeričkim putem. Postavlja se pitanje što se dobilo zamjenom Navier-Stokesovih jednadžbi, 

jednadžbama graničnog sloja, ako se one opet moraju rješavati numerički. Jedna od dobrobiti 

pojednostavljivanja jednadžbi je da su one promijenile karakter. Navier-Stokesove jednadžbe 

su eliptičkog tipa, a Prandtlove jednadžbe su paraboličnog tipa. Eliptičnost jednadžbi 

fizikalno znači da će promjena stanja u nekoj promatranoj točki strujanja izazvati promjenu 

stanja u svim ostalim točkama strujanja, i obrnuto, promjena u bilo kojoj točki strujanja 

izazvat će promjenu i u promatranoj točki (ili kažemo da stanje u promatranoj točki utječe na 

stanje u čitavom području strujanja i istovremeno zavisi od stanja u svim točkama strujanja). 

U tom slučaju rubne uvjete je potrebno zadavati po svim rubovima područja strujanja. U 

slučaju paraboličnih jednadžbi, kakve su Prandtlove jednadžbe, stanje u promatranoj točki 

područja strujanja zavisi samo o stanju uzvodno od točke, a utječe na stanje u nizvodnim 

točkama. Zbog toga se kod Prandtlovih jednadžbi ne mora zadavati rubni uvjet na izlaznom 

presjeku x = L , jer što god mi zadali na tom rubu, to ne može imati nikakvog utjecaja na 

uzvodno polje strujanja. Numerički postupak za rješavanje paraboličkih jednadžbi ima 

marširajući karakter u kojem se polazi od ulaznog presjeka ( x = 0 ) u kojem su zadani profili 

komponenti brzine, te se na temelju tih profila odrede profili u susjednom presjeku udaljenom 

za Δx . Nakon toga se prelazi na susjedni presjek udaljen od ovoga za Δx , i sve tako dok se 

ne dođe do kraja graničnog sloja. Kod eliptičkog problema bi nepoznanice u svim točkama 

unutra graničnog sloja bile povezane simultanim sustavom jednadžbi, čije rješavanje zahtijeva 

puno više računalnog vremena. 

Redoslijed rješavanja jednadžbi graničnog sloja je sljedeći: 

1) Riješiti vanjsko neviskozno (potencijalno) strujanje i odrediti dp 

. Rubni uvjet 

dx 

nepromočivosti stijenke se primjenjuje na površini tijela. 

2) S dobivenim dp 

integrirati profile komponenti brzine u i v 

dx 

3) Za slučaj jako zakrivljene geometrije treba ponoviti proračun pod 1) s korekcijom 

rubnih uvjeta zbog postojanja graničnog sloja, čime se dobije korigirani dp 

. Nakon 

dx 

toga se ponovi integracija pod 2) 

Naravno da parabolični karakter jednadžbi graničnog sloja pretpostavlja da je strujanje fluida 

u graničnom sloju "priljubljeno uz stijenku", što nije uvijek slučaj, kao što će biti objašnjeno u 

nastavku. Naime, kod optjecanja jako zakrivljenih tijela dolazi do odvajanja strujanja, i tada je 

profil brzine u graničnom sloju takav da u određenom dijelu presjeka imamo strujanje prema 

nazad, što je protivno paraboličkom karakteru Prandtlovih jednadžbi, pa je jasno da u tom 

slučaju Prandtlove jednadžbe neće vrijediti, nego će za opis takva strujanja trebati primijeniti 

Navier-Stokesove jednadžbe.


Prandtlove jednadžbe izražene strujnom funkcijom 

Prandtlove jednadžbe se mogu izraziti i s pomoću strujne funkcije ψ , za koju vrijedi 

∂ψ∂ψ u = ; v=− 

∂y∂ x 

Uvrštavanjem gornjih izraza u jednadžbu kontinuiteta, ona se svodi na identitet 0=0, te ostaje 

samo x -komponenta jednadžbe količine gibanja, koja prelazi u 

2 2 3 

∂ψ∂ψ ∂ψ ∂ψ dvδ 

∂ψ 

⋅ − ⋅ = v 2 δ + υ 3 

∂y∂xy ∂ ∂x∂y�� dx 

∂y 

1dp 

− 

ρ dx 

Ovo je parcijalna diferencijalna jednadžba 3. reda, čijim se rješavanjem uz odgovarajuće 

rubne uvjete dobije strujna funkcija ψ , iz koja se nađu u, v. Jednadžba je nelinearna i nema 

općeg analitičkog rješenja. 

ODVAJANJE STRUJANJA 

Eksperimenti pokazuju da se u graničnom sloju može pojaviti odvajanje strujanja, tj. strujnice 

prestaju slijediti konturu tijela. Kao što je već rečeno nakon točke odvajanja Prandtlove 

jednadžbe više ne vrijede. Slijedeće slike shematski prikazuju slike strujnica pri ravninskom 

optjecanju profila pod dva različita napadna kuta. 

ρ, v ∞ 

v ∞ 

A 

A 

B 

B 

v max. 

Na gornjim slikama je s A označena točka zastoja, a s B točka u kojoj je brzina prema rješenju 

neviskoznog strujanja maksimalna. Od točke A do točke B brzina v δ na rubu graničnog sloja 

C 

D 

D


se povećava, a prema Bernoullijevoj jednadžbi tlak se smanjuje. Nakon točke B brzina v δ se 

smanjuje a tlak raste. Na čestice fluida između točaka B i D djeluje sila tlaka koja je suprotna 

smjeru gibanja, što jasno dovodi do smanjenja brzine (kinetičke energije) čestica fluida, tako 

da se može pojaviti odvajanje strujanja, što se redovito događa pri većim napadnim kutovima, 

kao što prikazuje druga slika, na kojoj se odvajanje strujanja pojavljuje u točki C. Nakon 

pojave odvajanja, u području između točaka C i D nema povećanja tlaka, dakle tlak ostaje 

niži, što povećava silu otpora oblika. 

Sljedeće slike shematski pokazuju još neke primjere odvajanja strujanja. 

y 

y 

v ∞ 

x 

v ∞ 

zona rec irkula c ijskog strujanja 

točke ponovnog 

nalijeganja strujanja 

Kratki cilindar 


točka ponovnog 

nalijeganja strujanja 

Dugi cilindar 


U točkama odvajanja i ponovnog nalijeganja strujanja je smično naprezanje jednako nuli. 

x


Utjecaj gradijenta tlaka na izgled profila brzine i odvajanje strujanja u graničnom sloju 

Promatrajmo strujanje unutar graničnog sloja pri horizontalnom optjecanju tijela sa 

zakrivljenom stijenkom. U blizini tjemena će biti presjek s maksimalnom brzinom u vanjskom 

potencijalnom strujanju, u kojem će biti dp 

= 0 . Uzvodno od toga presjeka je gradijent tlaka 

dx 

negativan, a nizvodno pozitivan, kao što prikazuje donja slika. 

y 

p 1 

dp 

0 

dx < 

v δ,max 

p > p 1 2 

p2 dp 

0 

dx = 

točka infleksije 

Točka odvajanja 

p1 

p < p 

1 2 

dp 

0 

dx > 

U području negativnog gradijenta tlaka, rezultirajuća sila tlaka na česticu fluida djeluje u 

dp 

smjeru njene brzine, pa se čestica ubrzava. Pri > 0 sile trenja i sila tlaka usporavaju 

dx 

čestice fluida kojima se smanjuje kinetičke energije, te može doći do odvajanja strujanja, kako 

je shematski prikazano na gornjoj slici. Iz slike je jasno da u točki zastoja derivacija 

∂ u 

komponente brzine u smjeru osi x mijenja predznak, pa je u toj točki = 0 , odnosno u 

∂y 

točki odvajanja je smično naprezanje jednako nuli. Smično naprezanje je definirano izrazom 

⎛∂u ∂v⎞ ∂u 

τ w = µ ⎜ + ⎟ = µ 

⎝∂y ∂x⎠ ∂y 

u kojem je derivacija 

nuli. 

y= 

0 

∂v 

∂x 

= 

y 0 

y= 

0 

= 0 

= 0 , jer je v -komponenta brzine u svakoj točki površine jednaka 

Sada ćemo kvalitativno analizirati utjecaj gradijenta tlaka na izgled profila u -komponente 

brzine u graničnom sloju. Prema Prandtlovim jednadžbama za stacionarno strujanje u 

ravninskom graničnom sloju vrijedi ∂p/ ∂ y = 0, 

što znači da je tlak funkcija samo koordinate 

x . Ako se x -komponenta količine gibanja iz sustava Prandtlovih jednadžbi za granični sloj, 

koja glasi 

2 

u u 1 dp u 

u v 

2 

x y dx υ 

∂ ∂ ∂ 

+ =− ⋅ + 

∂ ∂ ρ ∂y 

primijeni na samu stijenku, gdje y → 0 , a prema rubnim uvjetima u = 0 i v = 

0 , na samoj 

p 2 

x


stijenci ostaje ravnoteža sila tlaka i smičnih naprezanja 

2 

∂ u 1 dp 

= ⋅ 

∂ x 

2 

y µ d 

y= 

0 

y= 

0 

Ako se zna da je desna strana gornje jednadžbe funkcija samo od x , još jednim deriviranjem 

po dobije se 

y 

3 

∂ u 

∂ 

3 

y y= 

0 

= 0 

Iz čega se zaključuje da će profil druge derivacije brzine u na stijenci imati infleksiju. Ono 

što je važno zapamtiti je da predznak druge derivacije brzine u na stijenci zavisi od 

predznaka gradijenta tlaka. 

Na vanjskom rubu graničnog sloja ( y = δ ) vrijedi u = vδ, a iz pretpostavke da brzina na rubu 

graničnog sloja nije funkcija y slijedi i 

2 

u u 

∂ ∂ 

= 0 ; = 0 . Približavanjem vanjskom 

∂y ∂y 

2 

y= δ y= 

δ 

rubu graničnog sloja, brzina u se približava brzini vδ , a prva derivacija u ∂ 

∂ y 

opada, što znači 

2 

∂ u 

da druga derivacija približavanjem vanjskom rubu graničnog sloja mora biti negativna. 

2 

∂y 

Sljedeća slika kvalitativno prikazuje profile u komponente brzine u graničnom sloju za tri 

slučaja gradijenta tlaka. 

1 

1 

točka infleksije 

1) Za slučaj negativnog gradijenta tlaka druga derivacija brzine je negativna unutar cijelog 

područja graničnog sloja, a prva derivacija je pozitivna u cijelom području (lako se zaključi iz 

činjenice da je na rubu prva derivacija jednaka nuli, a zbog negativne druge derivacije, ona je 

cijelo vrijeme opadala, što znači da je za y < δ morala biti pozitivna). Jasno je da je najveća 

vrijednost prve derivacije na stijenci. 

dp 

2) Za slučaj = 0 druga derivacija brzine na stijenci je jednaka nuli, ali je unutar čitavog 

dx 

područja graničnog sloja negativna, pa je profil brzine sličan onome iz prethodnog slučaja s 

jedinom razlikom da će prva derivacija brzine (tj. smično naprezanje) na stijenci biti manja. 

dp 

3) Posebno je zanimljiv slučaj > 0 , jer će druga derivacija na stijenci biti pozitivna, a 

dx 

znamo da ona na vanjskom rubu teži k nuli od negativnih vrijednosti, iz čega se zaključuje da 

će druga derivacija biti jednaka nuli negdje unutar područja graničnog sloja. U točki u kojoj je


druga derivacija brzine jednaka nuli prva derivacija brzine ima ekstrem, a profil brzine ima 

točku infleksije. Jasno je da se prva derivacija na stijenci smanjuje, a kada se pojavi 

∂u 

= 0 nastaje odvajanje strujanja. Također je jasno da se odvajanje strujanja može 

∂y 

y= 

0 

dp 

pojaviti samo ako je druga derivacija brzine na stijenci pozitivna, odnosno za > 0 . Dakle 

dx 

dp 

uvjet > 0 je nužan (ali ne i dovoljan) za pojavu odvajanja strujanja. 

dx 

INTEGRALNI PRISTUP RJEŠAVANJU GRANIČNOG SLOJA 

Prandtlove jednadžbe koje opisuju strujanje fluida u graničnom sloju su pojednostavljene 

Navier-Stokesove jednadžbe, ali su to još uvijek nelinearne parcijalne diferencijalne 

jednadžbe, koje je još uvijek potrebno rješavati numerički. Stoga se traži daljnje 

pojednostavljanje tih jednadžbi kojim će se moći jednostavnije doći do odgovora o vezi 

između brzine strujanja i smičnog naprezanja, odnosno sili na tijelo. 

S obzirom da je debljina graničnog sloja pri visokim vrijednostima Reynoldsova broja puno 

manja od duljine stjenke, nameće se ideja tretirati strujanje u graničnom sloju 

jednodimenzijskim, slično analizi strujanja u dugim cjevovodima, gdje se umjesto sa stvarnim 

profilom brzine računa sa srednjom brzinom. Integriranjem Prandtlovih jednadžbi po debljini 

graničnog sloja dovodi do von Kármanove impulsne jednadžbe, koja daje vezu smičnog 

naprezanje na stjenci s integralnim parametrima graničnog sloja. 

No prije nego prijeđemo na izvod von Kármanove impulsne jednadžbe pogledajmo integralne 

relacije za granični sloj uz ravnu ploču, koje se dobiju integracijom jednadžbe kontinuiteta i 

komponente jednadžbe količine gibanja u smjeru strujanja. 

Integralne relacije za granični sloj uz ravnu ploču 

Promatramo laminarno stacionarno ravninsko strujanje u graničnom sloju uz ravnu ploču 

zanemarive debljine, kao što prikazuje sljedeća slika. 

y 

y 0 

p = konst. 

strujnica vanjski rub gr. sloja 


L 

u(y) 

x


Uočimo kontrolni volumen ograničen jednim vertikalnim presjekom ispred ploče, vertikalnim 

presjekom na x = L , između strujnice y = 0 i strujnice na udaljenosti y = y0dovoljno 

ispred 

ploče. Duljina L je izabrana upravo tako da u izlaznom presjeku gornja strujnica ulazi u 

granični sloj debljine δ . S obzirom da kroz strujnice nema protoka, jednadžba kontinuiteta 

kazuje da će protok kroz ulazni presjek biti jednak protoku kroz izlazni presjek, tj. 

∞ 

δ 

0 = ∫ 

0 

⋅ 

v y u dy 

Ako se gornjoj jednadžbi doda član − v∞δ i podijeli ju se s v∞ , dobije se 

δ 

u 

y0− δ =−∫ (1 − ) ⋅dy 

v 

0 

∞ 

Integral u gornjem izrazu se naziva debljinom istisnuća i označuje s δ 1 

δ 

u 

δ1 

= ∫ (1 − ) ⋅dy 

v 

0 

∞ 

Debljina istisnuća δ1 = δ − y0 pokazuje otklon strujnice (koja na presjeku x = L ulazi u 

granični sloj, na udaljenosti δ od ploče, a dovoljno daleko ispred ploče je bila na udaljenosti 

y od ravnine ploče) zbog postojanja graničnog sloja. 

0 

U opisanom strujanju je tlak konstantan, pa se sile tlaka međusobno poništavaju. Izvan 

graničnog sloja viskozne sile su zanemarive, a unutar graničnog sloja su viskozne sile 

uglavnom tangencijalne na površinu kontrolnog volumena. Tako bi sila Fx 

između fluida i 

ploče bila jednaka integralu smičnih naprezanja po površini ploče, a na presjeku x = L , 

komponenta viskoznih sila u smjeru osi x je zanemariva. S obzirom da kroz strujnice nema 

protoka, da su viskozne sile na strujnicama izvan graničnog sloja jednake nuli, prema 

integralnom obliku jednadžbe količine gibanja, sila Fx 

je jednaka razlici impulsnih funkcija 

na ulaznom i izlaznom presjeku, tj. vrijedi 

δ 

2 

Fx= ρv∞y0−∫ρu �� 

I 0 

1 

I2 

2 

dy 

�� 

Ako se u gornjem izrazu za umnožak v y iskoristi jednadžba kontinuiteta (a), dobije se 

δ 

∞ 

δ 

∞�∞ 0 

δ 

u⋅dy 0 

2 2 

∞ 

0 

u u 

Fx= ρv v y − ∫ρu d y = ρv 

∫ (1− 

)dy 

v∞ v∞ 

�� 

∫ 

δ 

0 

0 

gdje se posljednji integral u gornjem izrazu naziva impulsna debljina i označuje s δ 2 

δ 

u u 

δ 2 = ∫ ⋅(1 − ) ⋅dy 

v v 

0 

∞ ∞ 

2 

Fx 

Očito je za granični sloj uz ravnu ploču δ2 

= , parametar koji direktno pokazuje veličinu 

2 

ρv∞ sile otpora. 

(a) 

(b)


Von Kármanova impulsna jednadžba za granični sloj 

Polazi se od pretpostavke stacionarnog, nestlačivog ravninskog strujanja oko blago 

zakrivljene stijenke, pri čemu je područje strujanja podijeljeno na područje graničnog sloja, 

unutar kojeg vrijede Prandtlove jednadžbe, područje vanjskog neviskoznog strujanja u kojem 

vrijede Eulerove jednadžbe. Dva se područja spajaju na vanjskom rubu graničnog sloja, gdje 

je brzina v = v ( x) 

, za koju vrijedi 

v 

δ 

δ δ 

dvδ1 dp 

=− 

dxρdx y 

y = 0 : u = v= 

0 

Unutar graničnog sloja vrijede Prandtlove jednadžbe, koje zapisane u konzervativnom obliku 

glase 

JKG. x-komponenta 

2 2 

∂( u ) ∂( 

uv) dvδ∂ 

u 

+ = vδ 

+ υ 2 

∂x∂y dx ∂y 

(1) 

JK. 

∂u ∂v 

+ = 0 , koja nakon množenja s vδ ( x) 

prelazi u 

∂x ∂y 

∂( uvδ ) ∂( 

vvδ ) dvδ 

+ = u 

∂x∂y dx 

Oduzimanjem jednadžbe (1) od jednadžbe (2) slijedi 

(2) 

δ ( x=∞) 

2 

∂ ∂ dvδ ∂ u 

[ uv ( δ − u) ] + [ vv ( δ − u) ] + ( vδ − u) =−υ 

dy 

2 

∂x ∂y dx ∂y 

∫ 

Integriranjem gornje jednadžbe po debljini graničnog sloja (iako se integrali koji u 

podintegralnoj funkciji imaju član vδ− u mogu formalno integrirati i izvan graničnog sloja, 

jer je izvan graničnog sloja v − u = 0 ), dobije se 

δ 

δ δ 

δ 

∂ δ dvδ ∂u 

∫ [ uv ( δ − u) ] d y+ [ vv ( δ − u) ] + ( v u)dy 0 

δ − =−υ 

∂xdx ∫ 

∂y 

0 0 0 

Uvrštavanjem vrijednosti na donjoj i gornjoj granici integracije, uzimajući da vrijedi za 

∂ u 

y = 0: 

u = v= 

0 , za y = δ : u = vδi = 0 , nakon sređivanja se dobije se 

∂y 

⎡ ⎤ 

δ δ 

∂ ⎢ 

2 u u ⎥ dvδ 

u ∂u 

⎢vδ (1 − )d y⎥+ vδ (1 − )dy 

= υ 

∂x∫v v dx 

∫ 

⎢ v y 

0 δ δ ⎥ 

0 δ ∂ y= 

0 

⎢ 

�� 

δ2( x) ⎥ 

�� 

⎣ ⎦ 

δ1( x) 

τ ρ 

w 

0 

x


U gornjoj su jednadžbi svi članovi funkcija samo koordinate x , a nakon deriviranja slijedi 

dvδ 2 dδ2dvδ τ w 

2vδ 

δ2 + vδ + vδ 

δ1 

= 

dx dx dx 

ρ 

Nakon dijeljenja gornje jednadžbe s 2 

vδ slijedi konačan oblik von Kármanove impulsne 

jednadžbe za granični sloj 

dδ21 dvδ 

τ w dδ21 dvδ 

τ w 

+ [ 2δ2 

+ δ1] 

= ili + δ 

2 

2[ 2 + H12] 

= 2 

dxv dx 

ρv 

dxv dx 

ρv 

δ δ 

δ δ 

gdje je H12 = δ1 / δ2 

form parametar, a debljina istisnuća i impulsna debljina su definirane 

sljedećim izrazima. 

1 

δ 

u 

∫ (1 ) dy 

i 2 

v 0 δ 

δ = − ⋅ 

δ 

u u 

δ = ∫ ⋅(1 − ) ⋅dy 

v v 

0 

δ δ 

Von Kármanova impulsna jednadžba je obična diferencijalna jednadžba u kojoj su sve 

veličine funkcija samo x koordinate, a postupak njene primjene je sljedeći 

1. Riješiti potencijalno strujanje i odrediti brzinu vδ i dvδ 

dx 

u ⎛ y⎞ 

2. Pretpostaviti (što realnije) profil brzine unutar graničnog sloja oblika = f ⎜ ⎟ 

⎝δ⎠ ; 

gdje je f neka funkcija koja svakako zadovoljava rubne uvjete ( 0) 0 

3. Izračunati δ 1 i δ 2 iz pretpostavljenog profila, te izračunati 

f = 

vδ i f 1 = 1. 

∂u 

τ w = µ ⋅ 

∂y 

4. Riješiti Von Karmanovu jednadžbu po parametru δ te natražno računati w 

otpora. 

y= 

0 

() 

τ i silu


TURBULENTNO STRUJANJE FLUIDA 

Turbulentno strujanje fluida je najčešći oblik strujanja u prirodi, a pojavljuje se uvijek pri 

visokih vrijednostima Reynoldsova broja. Strujanje zraka oko automobila, aviona ili vlaka, 

strujanje vode oko brodskog trupa, strujanje u vodovodnim, plinovodnim i drugim cijevnim 

mrežama, neki su od tehničkih problema u kojima je strujanje redovito turbulentno. Neka 

strujanja fluida u prirodi, poput strujanja vode u rijekama (npr. nestacionarno strujanje oko 

stupa mosta) ili istjecanje dima iz dimnjaka (širenje perjanice nepravilna oblika) primjeri su 

turbulentnog strujanja fluida iz kojih se može steći predodžba o složenom karakteru takvog 

strujanja. Sama riječ turbulentan (koja ima značenja: nemiran, buran, u stanju jakog 

komešanja, žestoko uzburkan, pun poremećaja) jasno odražava karakter takva strujanja. 

Za dane stacionarne rubne uvjete, principijelno, uvijek postoji stacionarno rješenje Navier- 

Stokesovih jednadžbi (koje doduše zbog matematičkih poteškoća često ne možemo odrediti). 

Tako npr. stacionarno rješenje za strujanje fluida u okrugloj cijevi (dano na vježbama) postoji 

za bilo koju vrijednost Reynoldsova broja. Iskustvo nas uči, da se takvo rješenje može održati 

samo pri niskim vrijednostima Reynoldsova broja (približno do Re = 2300 ), a pri višim 

vrijednostima strujanje postaje nestabilno i prelazi u režim turbulentnoga strujanja, kako je to 

pokazao Reynolds svojim eksperimentom, u kojem je kroz sredinu prozirne cijevi puštao 

tanki mlaz obojene tekućine, kao što shematski prikazuje sljedeća slika. 

OBOJENI FLUID 

D 

a) b) c) d) 

v⋅D⋅ρ Strujanje kroz cijev karakterizirano je Reynoldsovim brojem Re = , kojeg je mogao 

µ 

mijenjati uz pomoć ventila na kraju cijevi. Pri niskim vrijednostima Reynoldsova broja, mlaz 

obojenog fluida, ostaje miran i ravan, što svjedoči o laminarnom strujanju, slika a). Pri 

određenom Reynoldsovom broju je mlaz počeo gubiti stabilnost, pojavljuje se periodičko 

iskrivljavanje obojenog mlaza, kao što shematski prikazuje slika b). Dodatnim malim 

povećanjem Reynoldsova broja, nestabilnost se naglo povećava, da bi vrlo brzo mlaz obojene 

tekućine praktički ispunio čitav presjek cijevi, što svjedoči o poprečnom gibanju čestica 

fluida. Reynoldsov broj kod kojega se pojavljuje prva nestabilnost strujanja se naziva 

kritičnim Reynoldsovim brojem. Vrijednost kritičnog Reynoldsova broja nije neka čvrsta 

vrijednost. Ona zavisi od oblika ulaza u cijev, hrapavosti stijenke cijevi, i nekih drugih faktora 

poput malog odstupanja od kružnog oblika poprečnog presjeka cijevi, čistoći fluida, vanjskim 

utjecajima, npr. vibracijama cijevi i sl. Stoga se mogu definirati i dvije vrijednosti kritičnog 

Reynoldsova broja: donja i gornja vrijednost. Donja vrijednost kritičnog Reynoldsova broja je 

ona ispod koje se ne pojavljuje nestabilnost strujanja (nije zabilježeno turbulentno strujanje), a


gornja vrijednost je ona iznad koje nije zabilježeno laminarno strujanje. Za okrugle cijevi s 

oštrim ulaznim bridom se za donju vrijednost kritičnog Reynoldsovog broja uzima 

vrijednost , a za gornju vrijednost približno (naime u laboratorijskim 

Re krg =40000 

Re 

krd =2320 

uvjetima se uspjelo u cijevi održati laminarno strujanje do tog Reynoldsova broja). 

Naravno da je kritična vrijednost Reynoldsovog broja različita za različita strujanja. Tako je 

npr. za strujanje u pravokutnom kanalu, kojemu je širina veća od visine, kritični Reynoldsov 

ρ ⋅vsr ⋅h 

broj na temelju srednje brzine i visine kanala bio Rekr 

= ≈ 500 . 

D 

Dakle da rezimiramo: U prirodi se može ostvariti samo ono stacionarno strujanje fluida koje 

je stabilno u odnosu na male perturbacije. Matematičko ispitivanje stabilnosti rješenja Navier- 

Stokesovih jednadžbi bi se vršilo perturbiranjem (dodavanjem malog harmoničkog 

poremećaja) osnovnom stacionarnom rješenju. Ukoliko perturbacija (nametnuti mali 

poremećaj) slabi u vremenu, strujanje je stabilno i ostaje stacionarno. Takvo strujanje 

nazivamo laminarnim. Ukoliko perturbacije ne slabe, već se pojačavaju, strujanje postaje 

nestacionarno, bez obzira na stacionarne rubne uvjete i postupno dobiva kaotičan karakter. 

Takvo strujanje nazivamo turbulentnim. Primijetimo da turbulentno strujanje fluida ima 

unutrašnje stupnjeve slobode, jer je nestacionarno za stacionarne rubne uvjete pa analitičko 

opisivanje takvog strujanja nije moguće. 

Bez da ulazimo u matematičko ispitivanje stabilnosti rješenja, jednostavnim razmišljanjem se 

može pokazati da je neviskozno strujanje, prema slici a), u kojem se slojevi fluida gibaju 

relativnom brzinom jedan u odnosu na drugi apsolutno nestabilno. 

Slika a) prikazuje strujnice u ravninskom neviskoznom 

strujanju. Prema jednadžbi kontinuiteta protok između 

dvije strujnice je konstantan, pa će za slučaj paralelnih 

strujnica i brzina biti konstantna, a prema 

Bernoullijevoj jednadžbi će tada i tlak biti konstantan. 

Na granici dvaju slojeva imamo skok brzine 

(beskonačni gradijent), što uzrokuje nestabilnost 

ovakvog strujanja. Pretpostavimo da se granica dvaju 

slojeva ma kako malo deformira (ne ulazeći u razlog 

toj deformaciji), kako prikazuje slika b). Na mjestima 

gdje se razmak među strujnicama povećao, brzina će 

(prema jednadžbi kontinuiteta) opasti, a tlak će se 

(prema Bernoulllijevoj jednadžbi) povećati. Dakle 

nastat će sile, koje će tu strujnicu još više deformirati, 

kao što prikazuje slika c), a vrlo brzo će strujanje 

poprimiti vrtložnu strukturu, kao što prikazuje slika d). 

Naravno da u viskoznom strujanju ne može postojati beskonačni gradijent brzine, a može se 

očekivati da će sklonost nastanku nestabilnosti viskoznog strujanja rasti s povećanjem 

gradijenta brzine i s udaljavanjem od stijenke, na kojoj je brzina jednaka nuli. 

h


Osnovne karakteristike turbulentnih strujanja fluida 

Turbulentno strujanje je kaotično strujanje fluida u kojem sve promjenjive veličine pokazuju 

slučajne promjene po vremenskoj i prostornim koordinatama, pri čemu je moguće razlučiti 

njihove statistički osrednjene vrijednosti. 

Turbulentno strujanje je izrazito nestacionarno strujanje, karakterizirano intenzivnim 

miješanjem fluida na razini većih ili manjih čestica. Intenzivno miješanje na nivou čestica 

daje turbulentnom strujanju difuzijski karakter s logičnom posljedicom povećanja disipacije 

energije. 

1) Nestacionarnost: 

Donja slika shematski prikazuje granični sloj uz ravnu ploču. Na samom početku razvija se 

laminarni granični sloj, koji pri određenoj vrijednosti (kritičnoj vrijednosti) Reynoldsova 

v∞xkr 5 6 

broja Rekr 

310 do 310 

ν 

⋅ 

= ≈ ⋅ ⋅ postaje nestabilan. U presjeku x = xkr 

periodički se i 

relativno rijetko u prostoru pojavljuju nestabilnosti strujanja (pulsacije brzine i tlaka). 

Daljnjim udaljavanjem od tog presjeka u smjeru strujanja pulsacije postaju sve češće, i sve 

gušće u prostoru, tako da nakon nekog presjeka govorimo o potpuno razvijenom 

turbulentnom strujanju. 

v ∞ 

x 

d(x) 

A B C 

Laminarno Tranzijentno Razvijeno turbulentno 

Sljedeća slika shematski prikazuje rezultate mjerenja tlaka u točkama A i B, od kojih je točka 

A u laminarnom dijelu graničnog sloja, a točka B u prijelaznom (tranzijentnom) području. U 

točki B je tlak u nekim vremenskim periodima približno stalan (za vrijeme dok se u točki ne 

nalazi poremećaj), a u nekim periodima nestacionaran (za vrijeme dok nestabilnost prolazi 

točkom). 

p p 

"A" - la m ina rno 

strujanje 

x 

kr 

t "B" - tranzijentno 

strujanje 

t 

Shematski prikaz rezultata mjerenja tlaka u točki C, koja se nalazi u području razvijene 

turbulencije i točki D koja se nalazi također u području razvijene turbulencije, ali pri rubu 

graničnog sloja, dan je na sljedećoj slici. U razvijenom turbulentnom strujanju tlak u točki C 

D


će stalno pokazivati slučajne pulsacije, dok će u točki D postojati vremenski periodi s bitno 

smanjenim pulsacijama tlaka, što svjedoči o nestalnosti ruba graničnog sloja (ako se o rubu 

graničnog sloja uopće može govoriti u smislu ruba u laminarnom strujanju). Naime rub 

graničnog sloja poput ostalih veličina također će pokazivati slučajne promjene i u svakom 

trenutku će izgledati drukčije. U tom smislu točka D će se u jednom trenutku nalaziti unutar 

graničnog sloja, a u nekom drugom izvan. Tada ugovorimo da se u točki D pojavljuje 

intermitirajuća turbulencija. 

p 

"C" - ra zvijeno 

turbulentno 

strujanje 

t 

p 

"D" - intermitentno 

strujanje 

U primjeru turbulentnog strujanja u cijevima također se može govoriti o nestacionarnosti 

turbulentnog strujanja. Slike dolje lijevo kvalitativno prikazuju rezultate mjerenja jedne 

komponente brzine u točki prostora tijekom vremena. U laminarnom stacionarnom strujanju 

vrijednost ostaje stalna u vremenu, a u nestacionarnom brzina je glatka funkcija vremena. U 

turbulentnom strujanju pojavljuju se slučajne brzine oko statistički osrednjene vrijednosti 

(govorimo o vremenskim pulsacijama). Ako je statistički osrednjena vrijednost stalna u 

vremenu turbulentno strujanje nazivamo kvazistacionarnim (ne možemo ga zvati 

stacionarnim jer je ono izrazito nestacionarno). 

v 

v 

U TO ČKI U PRESJEKU 

sta c iona rno 

La m ina rno 

turb. kvazistacionarno 

Turb ule ntno 

nestacionarno 

t 

turb. nestacionarno 

t 

Gledano po presjeku cijevi trenutni profil brzine u turbulentnom strujanju ne bi bio gladak, i u 

svakom vremenskom trenutku bi drukčije izgledao. Statistički osrednjena vrijednost profila je 

međutim glatka funkcija, a slučajna odstupanja vrijednosti brzine od statistički osrednjene 

vrijednosti u promatranoj točki presjeka nazivamo pulsacijom, koja se ovdje prikazuje po 

presjeku. 

2) Difuzijski karakter turbulentnog strujanja 

Prijenos fizikalne veličine u strujanju fluida odvija se putem konvekcije (uslijed strujanja 

fluida - tj. čestica fluida kao nositelj fizikalnog svojstva svojim premještanjem prenosi i 

fizikalno svojstvo) i putem difuzije. Difuzija je posljedica kaotičnog gibanja atoma, odnosno 

t 

t = t 1 

t = t 2


molekula, putem kojeg se fizikalno svojstvo širi po prostoru. Makroskopski gledano difuzija 

će se manifestirati za slučaj postojanja gradijenta fizikalnih veličina. Difuzijske procese 

nazivamo i spontanim procesima, jer se odvijaju sami od sebe, sve dok postoji gradijent 

fizikalne veličine. Primjer difuzijskog procesa je provođenje topline, iz područja s višom 

prema području s nižom temperaturom. Sljedeća slika daje primjer dvaju paralelnih strujanja 

istom brzinom u , različitih temperatura T 1 i T 2 . Ako je strujanje laminarno (dakle svaka 

čestica se giba u svom sloju) čestice će se gibati pravocrtno, a dvije čestice fluida iz dvije 

struje različite temperature koje su istovremeno izašle iza pregrade ostat će sve vrijeme 

susjede. Konvekcijom se toplina može prenijeti samo u smjeru gibanja, a ako nema toplinske 

provodnosti, neće biti izmjene (difuzije) topline među česticama i one će zadržati svaka svoju 

temperaturu, a profil temperature će ostati nepromijenjen (na slici je to slučaj označen s 

λ = 0 , lam.). S obzirom da uvijek postoji toplinska provodnost doći će do prijelaza topline s 

toplije na hladniju česticu, i što god su čestice dulje u kontaktu to će više topline biti 

izmijenjeno. Kao posljedica toga profil temperature će težiti izjednačavanju, kao što prikazuje 

slika (slučaj označen s 0 

λ ≠ , lam.). 

u 

u 

T 2 

T 1 

l = 0 

lam. 

Da bismo ilustrirali turbulentnu difuziju ponovo ćemo promatrati toplinski nevodljiv fluid. U 

turbulentnom strujanju čestice fluida se gibaju kaotično u svim smjerovima (pri čemu je 

globalno strujanje u desno statistički osrednjenom brzinom, npr. brzinom u ). Prema tome u 

turbulentnom strujanju će čestice toplijeg fluida ulaziti među čestice hladnijeg fluida, i 

obrnuto, doći će do prodora hladnijih čestica među toplije čestice. Ovo miješanje imat će za 

posljedicu profil temperature sličan onome iz laminarnog strujanja s toplinskom provodnošću, 

pa govorimo o turbulentnoj difuziji. Iz rečenog je jasno da turbulentna difuzija ima porijeklo 

u konvektivnom prijenosu fizikalnog svojstva uslijed gibanja čestica u poprečnom smjeru u 

odnosu na smjer glavnog strujanja. U realnim strujanjima imamo i molekularnu difuziju 

(uslijed toplinske provodnosti) i turbulentnu difuziju (uslijed turbulentnog miješanja čestica 

fluida – možemo govoriti i o turbulentnoj provodnosti). U razvijenom turbulentnom strujanju 

(pri intenzivnom miješanju čestica fluida) turbulentna difuzija može biti puno jača od 

molekularne. 

Ako je toplinska provodnost fluida koeficijent difuzije (u Fourierovom zakonu toplinske 

provodnosti) za difuziju topline, onda je viskoznost koeficijent difuzije za količinu gibanja. 

Naime u laminarnom strujanju, u kojem se čestice gibaju pravocrtno, količina gibanja se 

putem konvekcije prenosi samo u smjeru strujanja. Uslijed viskoznosti među slojevima fluida 

se pojavljuje smično (viskozno) naprezanje, putem kojeg se količina gibanja prenosi s bržeg 

na sporiji sloj (brži slojevi povlače za sobom sporije). Naravno, ako se radi o turbulentnom 

strujanju brže čestice će "uskakati" među sporije čestice i time im povećavati količinu 

gibanja, a "uskakanje" sporijih čestica među brže čestice će im smanjivati količinu gibanja. 

Taj proces prijenosa količine gibanja putem turbulentnog miješanja čestica fluida se naziva 

turbulentna difuzija. Molekularna viskoznost, definira viskozna naprezanja, odnosno 

molekularnu difuziju količine gibanja. Možemo govoriti da je za turbulentnu difuziju količine 

gibanja odgovorna turbulentna viskoznost, koja uzrokuje turbulentna naprezanja. Jasno je da 

je molekularna viskoznost fizikalno svojstvo fluida, a turbulentna viskoznost ne. Turbulentna 

viskoznost je posljedica režima strujanja, a u laminarnom strujanju je jednaka nuli. 

l = 0 

lam. 

l = 0 

turb.


Iz rečenog je jasno da će u uvjetima veće difuzije i profil brzine u strujanju kroz okruglu cijev 

biti ujednačeniji (jer difuzija ima tendenciju ujednačavanja profila). To se lijepo vidi iz 

sljedećeg dijagrama (dolje, lijevo), u kojem su nacrtana dva profila brzine svedena na istu 

srednju brzinu. 

u / usr 

1 

lam inarno 

turbulentno 

Re=10 66 

10 

Re = 

u / usr 

Re=10 4 

Re = 10 

Dijagram desno kvalitativno prikazuje utjecaj Reynoldsova broja. Može se zaključiti da s 

povećanjem Reynoldsova broja, prema očekivanju, raste utjecaj turbulentne difuzije. 

3) Povećana disipacija energije 

Iz dijagrama na slici gore lijevo, na kojem su prikazani profili brzine u laminarnom i 

turbulentnom strujanju, tako da su svedeni na jednaku srednju brzinu, očito je da će gradijent 

brzine na stijenci cijevi biti veći u turbulentnom nego u laminarnom strujanju, što znači da će 

biti i veće smično naprezanje. Veće smično naprezanje označuje veću disipaciju energije 

(bržu pretvorbu mehaničke u unutrašnju energiju – koju u strujanju u cijevima nazivamo i 

gubitkom mehaničke energije). O tome se lako osvjedočiti i iz Darcy-Weissbachovog izraza 

za pad tlaka (pad tlaka mjeri gubitak energije, a razmjeran je smičnom naprezanju na stijenci 

cijevi) za strujanje u cijevima, koji glasi 

2 

L vsr 

Δ p = λ⋅ ⋅ρ⋅ D 2 

64 64υ 

U laminarnom strujanju je faktor trenja λ = = , pa će pad tlaka biti linearno razmjeran 

Re vsrD srednjoj brzini strujanja. U turbulentnom strujanju, u režimu potpuno izražene turbulencije 

faktor trenja je konstantan (sjetimo se Moodyeva dijagrama), što znači da će pad tlaka biti 

razmjeran kvadratu srednje brzine. 

Slična je situacija i pri optjecanju tijela, gdje definiramo koeficijent otpora 

FD 

CD 

= 

1 2 

ρvS ∞ 

2 

koji govori o sili otpora, odnosno o snazi potrebnoj za gibanje tijela kroz mirujući fluid (to je 

snaga potrebna za svladavanje sile otpora, koja se predaje fluidu, a u konačnici se pretvara u 

unutarnju energiju fluida, što nazivamo disipacijom energije). Pri optjecanju bilo kojeg tijela 

za slučaj niskih vrijednosti Reynoldsova broja (slučaj laminarnog strujanja) koeficijent otpora 

konst. 

je oblika CD 

= , gdje vrijednost konstante zavisi od oblika tijela. U tom je slučaju sila 

Re 

otpora razmjerna brzini optjecanja tijela. Za slučaj razvijenog turbulentnog strujanja 

koeficijent otpora je približno konstantan, što znači da je sila otpora razmjerna kvadratu 

brzine optjecanja.


Statističko opisivanje turbulencije 

Kao što je rečeno, turbulentno strujanje je izrazito nestacionarno strujanje, koje se zbog svoje 

stohastičke prirode ne može opisati analitički. Turbulencija je to izraženija što je veći 

Reynoldsov broj. U razvijenom turbulentnom strujanju sve veličine pokazuju slučajne 

pulsacije u širokom spektru frekvencija (gledano vremenski) i u širokom spektru valnih 

duljina (gledano prostorno). Pri numeričkom rješavanju Navier-Stokesovih jednadžbi za 

slučaj razvijenog turbulentnog strujanja diskretizacija područja proračuna (geometrijska 

mreža) bi morala biti tako sitna da se obuhvate i najmanje amplitude pulsacija, a vremenski 

korak integracije bi morao biti tako mali da se obuhvate i najviše frekvencije turbulentnih 

pulsacija, što je vrlo zahtjevno sa stajališta kapaciteta i brzine računanja računala. Rezultat 

takva rješavanja bi bio skup numeričkih vrijednosti traženih polja fizikalnih veličina (u 

nestlačivom strujanju bi to bila polja brzine i tlaka) u velikom broju prostornih točaka za 

veliki broj vremenskih trenutaka. Ono što zanima inženjera su obično neke integralne veličine 

poput protoka, ukupne sile tlaka, ukupne viskozne sile na neku površinu i sl. Te integralne 

veličine također pokazuju slučajne promjene u vremenu, a inženjera će zanimati ne neka 

trenutna vrijednost, nego prosječna vrijednost i eventualno amplituda odstupanja od te 

prosječne vrijednosti. Dakle, ako bi inženjeru dali numeričko rješenje u velikom broju 

vremenskih koraka, on bi te rezultate uprosječio po vremenu, pa se nameće sama po sebi ideja 

da se prije rješavanja Navier-Stokesovih jednadžbi, sve veličine u tim jednadžbama uprosječe, 

te da se rješavaju jednadžbe za uprosječene veličine, koje inženjera i zanimaju. Time se 

značajno olakšava zadaća numeričkog rješavanja tih jednadžbi, jer koraci prostorne i 

vremenske diskretizacije više ne moraju biti onako mali. 

Danas se najčešće koristi vremensko uprosječenje (Reynoldsovo osrednjavanje). Ako je f 

neka veličina u turbulentnom strujanju, ona se može prikazati zbrojem vremenski osrednjene 

vrijednosti f i pulsirajućeg dijela f ′ ( f = f + f '). 

Vremenski osrednjena vrijednost f u 

razdoblju T 0 je po definiciji 

T0 

2 

1 

f ( x, t) = ⋅ f( x, t−τ) ⋅dτ 

∫ 

i i 

T0 

T0 

− 

2 

gdje T 0 mora biti odabrano tako da vrijedi f = f . Jasno je da kada se radi o 

kvazistacionarnom turbulentnom strujanju ( f nije funkcija vremena), razdoblje 

osrednjavanja može težiti u beskonačno. Dakle potez nad veličinom označuje vremensko 

osrednjavanje koje je definirano integralom, a za integriranje vrijedi da je integral zbroja 

jednak zbroju integrala. Dvostruki potez, npr f označuje osrednjavanje osrednjene veličine. 

Za dobro odabrano razdoblje osrednjavanja, dakle vrijedi 

f '= f − f = f − f = f − f = 0 

Ili riječima: Vremenski osrednjena vrijednost pulsirajućeg dijela bilo koje fizikalne veličine 

jednaka je nuli. 

Osrednjena vrijednost prostorne derivacije (gradijenta) veličine f je 

df 

⎛ ⎞ 

f 

dx T x x T x 

⎝ ⎠ 

T0 T0 

2 

1 ∂ 

= ⋅ ∫ 

i 0 T0 − 

2 

2 

f( xi, t−τ) 

∂ ⎜ 1 

⋅ dτ = ⋅ 

∂ i ∂ ⎜ ∫ 

i ⎜ 0 T0 

− 

2 

⎟ ∂ 

f( xi, t−τ) ⋅ dτ 

⎟= 

⎟ 

∂ i


Za osrednjenu vrijednost vremenske derivacije, vrijedi analogno 

T0 T0 

⎛ ⎞ 

2 2 

df 1 ∂ f( xi, t−τ) 

∂ ⎜ 1 

⎟ ∂f 

= ⋅ d f( xi, t ) d 

dt T ∫ ⋅ τ = ⋅ −τ ⋅ τ = 

0 T ∂t∂t⎜T∫ ⎟ 

0 0 T 

t 

0 

− ⎜ 

∂ 

− 

⎟ 

2 ⎝ 2 

⎠ 

Ili riječima: Osrednjena vrijednost derivacije jednaka je derivaciji osrednjene vrijednosti. 

Ako su f i g dvije veličine u kvazistacionarnom turbulentnom strujanju, pri čemu je 

f = f + f ' i g = g + g', 

vrijede sljedeće relacije 

f ⋅ g'= f ⋅ g'= 

0 

( ) 

f ⋅ g = f ⋅ g + g' = f ⋅ g + f ⋅ g'= f ⋅ g 

( ) ( ) 

f ⋅ g = f + f ' ⋅ g + g' = f ⋅ g + f '⋅ g' 

Valja primijetiti da osrednjena vrijednost umnoška dvaju pulsirajućih dijelova fizikalnih 

veličina nije jednaka nuli 1 . U konzervativnom obliku jednadžbe količine gibanja pojavljuje se 

umnožak vv i j čija osrednjena vrijednost je 

vv = v v + v 'v' i j i j i j 

Član vi'v j' 

označuje dvostruku korelaciju brzina 2 u točki, a fizikalno gledano će taj član 

opisivati turbulentnu difuziju količine gibanja, odnosno prijenos količine gibanja uslijed 

miješanja čestica fluida. Kontrakcijom indeksa u gornjem izrazu i njegovim dijeljenjem s dva 

dobije se 

1 2 1 2 1 2 

vi = vi + vi' 

�2 �2 �2 

a b c 

Ako sliku strujanja u turbulentnom strujanju gledamo kao zbroj vremenski osrednjenog 

(glavnog strujanja) opisanog poljem brzine v i i pulsirajućeg strujanja opisanog poljem brzine 

v′ i , tada je fizikalno tumačenje članova u gornjoj jednakosti sljedeće 

a) Osrednjena vrijednost ukupne specifične kinetičke energije strujanja 

b) Specifična kinetička energija glavnog (osrednjenog) strujanja 

c) Osrednjena vrijednost kinetičke energije pulsirajućeg strujanja ili kinetička energija 

turbulencije (označava se s k = vv ′ ′ /2) 

i i 

1 Na temelju toga umnoška se može govoriti o korelaciji dviju veličina, koja se izražava koeficijentom korelacije 

R = 

f′ ⋅ g′ 

f ′ ⋅ f′ ⋅ g′ ⋅g′ 

Apsolutna vrijednost gore definiranog koeficijenta je u granicama od nula do jedan. Vrijednost koeficijent 

korelacije jednaka nuli kazuje da su pulsacije veličina potpuno nezavisne, a vrijednost koeficijenta korelacije 

jednaka jedan da među njima postoji jednoznačna veza. 

2 To je tenzorska veličina. Ako se njena vrijednost ne mijenja pri zakretanju koordinatnog sustava govorimo o 

izotropnoj turbulenciji, a ako se njena vrijednost ne mijenja pri translaciji koordinatnog sustava govori se o 

homogenoj turbulenciji.


Vremenski osrednjene jednadžbe za slučaj nestlačivog strujanja 

Promatrat ćemo nestlačivo turbulentno strujanje ( ρ =konst.), u kojem ćemo zanemariti utjecaj 

masenih sila ( fi ≡ 0 ). Takvo je strujanje opisano jednadžbom kontinuiteta i jednadžbom 

količine gibanja u kojima su nepoznanice komponente polja brzine v i i polje tlaka p . Ove 

ćemo veličine prikazati zbrojem osrednjene vrijednosti i pulsirajućeg dijela 

v = v + v′ i p = p+ p′ 

i i i 

1. Jednadžba kontinuiteta za nestlačivo strujanje je 

∂v 

j ∂ ( vj + v′ 

j) 

= 0 ili = 0 

∂x 

j ∂x 

j 

Gledano u svjetlu prikaza strujanja zbrojem osrednjenog i pulsirajućeg strujanje, gornja 

jednadžba kontinuiteta vrijedi za ukupno strujanje, a čijim se osrednjavanjem dobije 

jednadžba kontinuiteta za osrednjeno strujanje 

∂v 

j 

= 0 

∂x 

j 

Ako se od jednadžbe kontinuiteta za ukupno strujanje oduzme jednadžba kontinuiteta za 

osrednjeno strujanje, dobit će se jednadžba kontinuiteta za pulsirajuće strujanje 

∂v′ 

j 

= 0 

∂x 

j 

Očito da u slučaju linearne jednadžbe kontinuiteta vrijedi princip superpozicije (zbroj dvaju 

rješenja jednadžbe je također rješenje jednadžbe), pa su jednadžbe kontinuiteta za osrednjeno 

i pulsirajuće strujanje istovjetne jednadžbi za ukupno strujanje. S obzirom da nas zanima 

samo vremenski osrednjeno strujanje, jednadžbu kontinuiteta za pulsirajuće strujanje nećemo 

promatrati. 

2. jednadžba količine gibanja za nestlačivo strujanje je 

vi p ⎡ ⎛ v v ⎞⎤ 

i j 

ρ ( ρvv j i) 

μ 

t xj xi xj xj xi 

∂ 

∂ ∂ ∂ ∂ ∂ 

+ =− + ⎢ ⎜ + 

⎜ 

⎟ 

⎥ 

∂ ∂ ∂ ∂ ⎢⎣ ⎝∂ ∂ ⎠⎥⎦ 

ili u prikazu s pomoću osrednjenih i pulsirajućih dijelova polja brzine i tlaka 

∂( 

v ′ 

[ ( )( ) ] ( ) ⎡ ⎛ ∂ ⎞ ⎛ ′ ∂ ′ ⎞⎤ 

i + vi 

) ∂ 

∂ p − p′ 

∂ 

⎢ ⎜ 

∂v 

v i j ⎟ ⎜ 

∂v 

v i j 

ρ + ρ v + ′ + ′ = − + 

+ + + ⎟ 

j v j vi 

vi 

μl 

μ 

⎜ ⎟ l ⎜ ⎟ 

⎥ 

∂t 

∂x 

j 

∂xi 

∂xi 

⎢⎣ 

⎝ ∂x 

j ∂xi 

⎠ ⎝ ∂x 

j ∂xi 

⎠⎥⎦ 

Vremenskim osrednjavanjem jednadžbe količine gibanja (uvažavajući prije definirana 

pravila) dobije se jednadžba količine gibanja za osrednjeno strujanje, koja glasi 

∂vi ∂ ∂p ∂ ⎡ ⎛ ∂v 

∂v 

⎞ ⎤ 

i j 

ρ + ( ρvv j i) =− + ⎢μ⎜ + ⎟−ρvv 

′ ′ i j⎥ 

∂t ∂xj ∂xi ∂x ⎜ 

i ⎢ ∂x j ∂x 

⎟ 

⎣ ⎝ i ⎠ ⎥⎦ 

Skup vremenski osrednjenih jednadžbi kontinuiteta i količine gibanja se naziva Reynoldsovim 

jednadžbama. Jednadžba količine gibanja za pulsirajuće strujanje bi se dobila oduzimanjem 

jednadžbe količine gibanja za osrednjeno strujanje od jednadžbe količine gibanja za ukupno 

strujanje, no ta nam jednadžba ne treba jer nam je ideja gledati samo osrednjeno strujanje. Iz 

gornje jednadžbe je jasno da nećemo moći gledati samo osrednjeno strujanje, ne vodeći 

računa o pulsirajućem strujanju, jer se u jednadžbi količine gibanja (zbog nelinearnog 

konvektivnog člana, u kojem se pojavljuje umnožak vv) j i pojavljuje predstavnik pulsirajućeg


strujanja, član − ρ vv ′′ i j . Taj član označuje turbulentnu difuziju količine gibanja, a budući da 

molekularna difuzija odgovara viskoznim naprezanjima, to će se član − ρ vv ′′ i j nazivati 

turbulentnim ili Reynoldsovim naprezanjima. Tenzor Reynoldsovih naprezanja je simetričan 

tenzor u kojemu je šest nepoznanica 

−ρvv ′′ 1 1 −ρvv ′′ 1 2 −ρvv 

′′ 1 3 

− ρvv ′ ′ = −ρvv ′ ′ −ρvv 

′ ′ 

i j 

simetrično 

2 2 2 3 

−ρ 

vv ′ ′ 

3 3 

Jasno je da Reynoldsove jednadžbe sadrže više nepoznanica, nego što ima jednadžbi, pa takav 

sustav nema jednoznačno rješenje. Mogli bismo izvesti i jednadžbu za Reynoldsova 

naprezanja (dvojnu korelaciju brzina). U jednadžbi za dvojnu korelaciju pojavile bi se trojna 

korelacija vv ′′ i jv′ k i još neke nove nepoznate korelacije. Za sve ove korelacije, polazeći od N-S 

jednadžbi, također se mogu izvesti pripadne jednadžbe u kojima bi se zbog nelinearnosti N-S 

jednadžbi pojavljivale nove i nove nepoznate korelacije, tako da bi broj nepoznanica brže 

rastao od broja jednadžbi. 

Stohastičku prirodu turbulentnog strujanja prikazali smo vremenski osrednjenim poljima 

brzine i tlaka, te time izgubili dio informacija koje sadrže N-S jednadžbe. Da bi povratili 

izgubljene informacije potrebno je poznavati beskonačno mnogo korelacija brzina i tlaka. S 

druge strane, iskustvo pokazuje da je dovoljno poznavati konačan broj korelacija da bi se 

proračunale karakteristike polja interesantne sa stajališta inženjerske prakse, i na toj se 

činjenici temelje modeli turbulencije. 

Zadatak modela turbulencije je usklađivanje broja jednadžbi i broja nepoznatih polja, 

zaustavljajući se na određenoj korelaciji. Sve više korelacije modeliraju se pomoću nižih koje 

su obuhvaćene modelom turbulencije. Opći zahtjevi koji se postavljaju pred model 

turbulencije su: univerzalnost, točnost, mogućnost ekonomičnog rješavanja i jednostavnost. 

Model turbulencije 

Modeli turbulencije dijele se s obzirom na red korelacije brzina za koju se rješava transportna 

jednadžba na: modele prvog, drugog i trećeg reda. U modelima prvog reda, koji su 

najjednostavniji, modelira se već dvojna korelacija brzina, odnosno tenzor Reynoldsovih 

naprezanja i to uglavnom prema hipotezi Boussinesqa u obliku: 

⎛ ∂v 

∂v 

⎞ 

i j 2 

− ρvv ′′ i j = μt⎜ + − ρkδ ⎜ 

⎟ 

ij 

xj x ⎟ 

⎝∂ ∂ i ⎠ 3 

gdje je μ t koeficijent turbulentne viskoznosti koji nije fizikalno svojstvo fluida već funkcija 

uvjeta strujanja, a u laminarnom strujanju jednak je nuli. Član s kinetičkom energijom 

turbulencije k = vv ′′ i i/2 

dodan je u cilju zadovoljavanja gornje jednadžbe za slučaj kontrakcije 

indeksa. S obzirom na analogiju gornjeg izraza s Newtonovim zakonom viskoznosti, modeli 

koji se temelje na toj pretpostavci nazivaju se newtonovskim modelima turbulencije. 

Hipotezom Boussinesqa šest komponenti tenzora Reynolsovih naprezanja modelirano je 

jednim nepoznatim poljem koeficijenta turbulentne viskoznosti. Postoji više načina 

modeliranja koeficijenata turbulentne viskoznosti, a mi ćemo se zadržati na najjednostavnijem 

prema analogiji s kinetičkom teorijom plinova.

Prandtlova hipoteza puta miješanja 


Boussinesqova ideja da turbulentna naprezanja (koja su posljedica kaotičnog turbulentnog 

miješanja čestica fluida) modelira slično viskoznim naprezanjima (koja su posljedica 

kaotičnog gibanja atoma i molekula unutar čestica fluida), direktno vodi k Prandtlovom 

modelu turbulentne viskoznosti koji se temelji na analogiji s molekularnom viskoznošću, koja 

je definirana kinetičkom teorijom plinova. Prema kinetičkoj teoriji plinova viskoznost fluida 

je manifestacija molekularnog gibanja, kojeg opažamo u makrosvijetu. Po toj teoriji 

viskoznost fluida je razmjerna gustoći fluida, slobodnoj putanji molekula i karakterističnoj 

brzini molekula. Analogno tome se definira turbulentnu viskoznost u obliku 

μt = ρlv 

m t 

gdje su: 

lm - duljina puta miješanja čestica fluida u turbulentnom strujanju 

vt - karakteristična brzina turbulentnih pulsacija 

Prema tome turbulentna viskoznost je definirana s dvije karakteristične veličine u 

turbulentnom strujanju, a gornja relacija čini osnovu za veći broj modela turbulencije, koji se 

razlikuju po definiciji te dvije karakteristične veličine u turbulenciji. 

Proučavajući strujanje u graničnom sloju Prandtl je predložio sljedeću relaciju između puta 

miješanja i karakteristične brzine turbulencije 

∂v1 

vt = lm 

∂x2 

što uvršteno u gornju relaciju, daje konačni izraz za koeficijent turbulentne viskoznosti 

2 ∂v1 

μt= ρlm 

∂x2 

u kojem se pojavljuje samo nepoznata duljina puta miješanja l m . Ova se duljina propisuje 

algebarskim relacijama na temelju eksperimentalnih mjerenja. Naravno da je to nedostatak 

ovog modela jer je primjenjiv samo u situacijama za koje već postoje eksperimentalna 

mjerenja temeljem kojih se može propisati put miješanja. 

Uvrštavanjem hipoteze Boussinesqa u Reynoldsove jednadžbe one prelaze u oblik 

∂v 

j 

= 0 

∂x 

j 

efektivni 

tlak 

�� 

2 

efektivna 

⎛ ⎞ 

∂ p ρk 

⎡ viskoznost 

⎤ 

v 

⎜ + ⎟ 

i 3 ⎢�� ∂ ∂ ∂ ⎛ ∂v 

∂v 

⎞⎥ 

i j 

ρ + ( ρvv j i) 

=− 

⎝ ⎠ 

+ ⎢( μ+ μt) 

⎜ + ⎟⎥ 

∂t ∂xj ∂xi ∂x ⎜ 

j ∂xj ∂x 

⎟ 

⎢ ⎝ i ⎠⎥ 

⎢⎣ ⎥⎦ 

Očito je da Reynoldsove jednadžbe koje opisuju vremenski osrednjeno turbulentno strujanje 

fluida imaju isti oblik kao i polazne Navier.Stokesove jednadžbe, koje opisuju ukupno 

strujanje, s razlikom da se u Reynoldsovim jednadžbama pojavljuju vremenski osrednjene 

veličine, umjesto tlaka se pojavljuje efektivni tlak, a umjesto viskoznosti fluida efektivna 

viskoznost. 

Iz toga se dade zaključiti da će i von Kármánova impulsna jednadžba za turbulentno strujanje 

fluida imati isti oblik kao i za laminarno strujanje s tim da će se u njoj pojavljivati vremenski 

osrednjene veličine.

MEHANIKA FLUIDA II – Što valja zapamtiti 

Strujanje u blizini čvrste stijenke (višeslojni model turbulentnog graničnog sloja) 

Promotrimo s teorijskog stajališta vremenski osrednjeno strujanje u blizini ravne stijenke. 

Pretpostavimo ravninsko strujanje (u koordinatnom sustavu s osi x 1 duž stijenke i osi x 2 

okomito na stijenku). Neka je strujanje stacionarno s izobraženim profilom brzine v1 = v1( x2) 

(kao u strujanju u cjevovodu) i neka je strujanje bez gradijenta tlaka (kao u graničnom sloju 

uz ravnu ploču). 

Iz jednadžbe kontinuiteta za vremenski osrednjeno strujanje slijedi 

∂v1 

∂v2 

∂v1 

∂v2 

+ = 0 , odnosno prema pretpostavci je = 0 , pa je = 0 , odnosno v2 ≡ 0 . 

∂x 

∂x 

∂x 

∂x 

1 

2 

Iz komponente jednadžbe količine gibanja u smjeru strujanja, za i = 1 dobije se 

∂v1 ∂v2 

∂ ⎡ ∂v 

⎤ 1 

ρv1+ ρv2= ⎢( μ+ μt) 

⎥ 

∂x1∂x2∂x2 

⎣ ∂x2⎦ 

S obzirom da je konvekcijski član jednak nuli ostaje 

∂ ⎡ ∂v⎤ 

1 

⎢( μ+ μt) 

⎥ = 0 

∂x2 ⎣ ∂x2 

�� ⎦ 

σ τ 

21= 

gdje izraz u uglatoj zagradi označuje ukupno viskozno i turbulentno naprezanje σ 21 , kojeg 

ćemo jednostavno označavati s τ . S obzirom da smo pretpostavili strujanje izobraženim 

profilom brzine ( v 1 nije funkcija od x 1 ) integracijom gornje jednadžbe dobije se 

v1 

τ ( μ μt) C 

x2 

∂ 

= + = 

∂ 

gdje se vrijednost konstante C određuje iz rubnog uvjeta: za x 2 = 0 ; τ = τ w , pa vrijedi 

∂v1 

τ = ( μ+ μt) = τw= 

konst. 

∂x2 

što će reći da je smično naprezanje konstantno po debljini graničnog sloja. 

Analizirajmo sada dva ekstremna slučaja, da je zanemariva turbulentna viskoznost i da je 

zanemariva molekularna viskoznost. Naime u neposrednoj blizini stijenke, turbulentne 

pulsacije su onemogućene (prigušene) samom stijenkom, a poznato je da su pulsacije brzine 

na samoj stijenci jednake nuli. Kada nema turbulentnih pulasacija nema ni turbulentne 

difuzije, odnosno turbulentne viskoznosti. Stoga se za vrlo blisko područje uz stijenku 

turbulentna viskoznost može zanemariti. Nasuprot tome udaljavanjem od stijenke turbulentne 

pulsacije se povećavaju, čime raste i put miješanja pa prema tome i turbulentna viskoznost. 

Dovoljno daleko od stijenke turbulentno strujanje postaje toliko razvijeno da je turbulentna 

1 

2 

76


viskoznost mnogostruko puta veća od molekularne viskoznosti, te se molekularna viskoznost 

može zanemariti. U tom području možemo pretpostaviti da se put miješanja povećava 

razmjerno s udaljenošću od stijenke, a ako je κ koeficijent razmjernosti, vrijedi lm = κ x2. 

U 

nastavku ćemo integrirati prethodnu jednadžbu za ova dva slučaja. 

1) Područje neposredno uz stijenku ( μ � μt 

), turbulentna viskoznost zanemariva 

1 

Izraz za ukupno naprezanje prelazi u ( μ + μ ) 

dobije 

τ w v1 = x2 

μ 

tj. profil brzine je linearan. 

∂v 

τ = t = τw= 

konst. , čijom integracijom se 

∂x 

2) Područje podalje od stijenke μ � μt 

, molekularna viskoznost se zanemaruje 

Izraz za ukupno naprezanje prelazi u ( ) 1 

hipotezi puta miješanja je μ = ρl 

2 

2 2⎛ ∂v 

⎞ 1 x2⎜ 

⎟ w 

∂x2 

t 

∂v 

2 1 

m 

∂x2 

2 

∂v 

τ = μ + μt= τw= 

konst. , a prema Prandtlovoj 

∂x 

, gdje je lm = κ x2, 

pa je 

τ = ρκ = τ = konst. 

⎝ ⎠ 

odakle je 

dv1 1 

= 

dx2 

κ 

τ w 1 

ρ x2 

te se integracijom dobije 

1 

v1 = 

κ 

τ w ln x2 + C 

ρ 

logaritmički profil brzine, u kojem se von Kármánova konstanta κ i konstanta C određuju 

mjerenjem. Postojanje ova dva područja linearnog i logaritmičkog profila brzine potvrđen je 

mjerenjem uz stijenku kako u graničnom sloju, tako i u strujanju u cjevovodima. Rezultati 

mjerenja se obično prikazuju u bezdimenzijskom obliku. Iz prethodnog izraza je jasno da član 

τ w ima dimenziju brzine, pa se vτ = 

ρ 

definiraju se bezdimenzijska brzina 

1 

τ w naziva brzina trenja. S pomoću brzine trenja 

ρ 

v + 

u = 

vτ i bezdimenzijska udaljenost od stijenke 

+ ρx2vτx2vτ 

y = = 

μ υ 

τ w 

τ w ρx2 

+ + 

Linearni profil brzine v1 = x2 

prelazi u v1 

= ili u = 

y 

μ 

ρ μ 

� 

2 

vτ 

2 

77


1 τ w 

Logaritmički profil v1 = ln x2 + C se može preurediti u bezdimenzijskom obliku u 

κ ρ 

+ 1 + 1 + 

u = ln y + B = ln( Ey ) 

κ κ 

Ova se dva profila obično prikazuju u dijagramu gdje je na ordinati bezdimenzijska brzina u + , 

a na apscisi ln y + (odnosno y + u logaritamskoj skali), pa se u takvom dijagramu linearni 

+ 

+ + ln y 

profil u = y = e prikazuje eksponencijalnom krivuljom, a logaritmički profil pravcem. 

+ v 

+ 1 u = 1 = 

v 

u 

v 

v τ 

τ 

μ μt 

u = y 

+ + + 

u = y 

δ 

μt 

μ 

+ 1 + 

u = ln( Ey ) 

+ χ 1 + 1 + 

( ) 

u = ln y + B= ln Ey 

κ κ 

τ 2 

ν 

x v 

+ 

+ 

y = 3do5 

y ≈ 40 

+ 

y = 

Gornja slika shematski prikazuje dijagram bezdimenzijske brzine u funkciji bezdimenzijske 

udaljenosti od stijenke, pri čemu bi kvadratići odgovarali mjerenjima. Linearni profil koji je 

izveden uz pretpostavku μ � μt 

, poklapa se s mjerenjima do vrijednosti y + tri do pet, a to se 

područje naziva linearnim podslojem. Područje u kojem se mjerenja dobro poklapaju s 

logaritmičkim profilom brzine (izvedenim pod pretpostavkom μ � μt 

) naziva se inercijalni 

podsloj (područje y + + vy τ y = 

υ 

od približno 40 do nekoliko tisuća). Između ta dva podsloja postoji 

područje unutar kojega su molekularna i turbulentna viskoznost istog reda veličine, a to se 

područje naziva prijelaznim podslojem. 

Kada se radi o optjecanju tijela, viskozni, prijelazni i inercijalni podsloj čine zajedno unutarnji 

dio graničnog sloja (procjenjuje se na 10 do 15 % ukupne debljine graničnog sloja). U 

unutarnjem dijelu graničnog sloja značajni utjecaj na samu turbulenciju ima sama stijenka, te 

ona ne ovisi značajno o vanjskom strujanju, što objašnjava činjenicu da će logaritmički profil 

brzine vrijediti u strujanju uz bilo koju stijenku, pod uvjetom da je gradijent tlaka umjereno 

velik (izraz je izveden pod pretpostavkom nultog gradijenta tlaka). U unutarnjem dijelu 

graničnog sloja je karakteristična brzina jednaka brzini vτ , a karakteristična duljina je vτ / υ . 

Na turbulenciju u vanjskom dijelu graničnog sloja značajniji utjecaj imaju parametri vanjskog 

strujanja, pa je u tom dijelu karakteristična brzina jednaka brzini vδ na vanjskom rubu 

graničnog sloja, a karakteristična duljina je jednaka debljini graničnog sloja. 

78


Strujanje u hidraulički glatkim i hrapavim cijevima 

Za potrebe hidrauličkog proračuna cjevovoda, definiran je faktor trenja λ koji ulazi u Darcy- 

Weissbachov izraz za proračun pada tlaka, koji glasi 

L 1 2 

p1− p2 = λ ρusr 

D 2 

2 

gdje je u sr prosječna brzina (po presjeku) vremenski osrednjenog profila brzine. Dakako da 

postoji veza između faktora trenja i smičnog naprezanja na stijenci cijevi. Ako je strujanje 

stacionarno i izobraženim profilom brzine (tako da se smično naprezanje ne mijenja u smjeru 

strujanja), tada se iz jednadžbe količine gibanja postavljene za kontrolni volumen (koji 

obuhvaća cijev duljine L između presjeka 1 i 2) zaključuje da je sila na stijenku cijevi 

2 

D π 

jednaka razlici impulsnih funkcija tj. ( p1− p2) 

, a s druge strane, za slučaj konstantnog 

4 

smičnog naprezanja, ta sila je τwDπ L. 

Primjenom Darcy-Weissbachovog izraza dobije se 

2 

L 1 2 D π 

λ ρusr = τwDπL, odakle je 

D 2 4 

2 

w sr 

8 u 

λ 

τ = ρ 

gornji izraz prikazan pomoću brzine trenja 

u 

u 

max 

Porast Re 

Re 

v τ 

τ 

ρ 

λ 

v = u . 

8 

w = prelazi u τ 

sr 

79 

Slika prikazuje rezultate mjerenja 

vremenski osrednjenog profila brzine u 

hidraulički glatkim cijevima, pri 

različitim vrijednostima Reynoldsova 

broja. Vrijednosti brzine su normirane s 

maksimalnom brzinom u max u simetrali 

cijevi. Iz slike je očito da porastom 

Reynoldsova broja profil brzine postaje 

ujednačeniji po presjeku, što se tumači 

porastom utjecaja turbulentne difuzije 

(kao što je prije rečeno što je veći 

Reynoldsov broj to je turbulentno 

strujanje razvijenije). 

Jednostavan izraz koji dobro opisuje profil brzine u turbulentnom strujanju u hidraulički 

glatkim cijevima je 

1 1 

u ⎛ y ⎞n ⎛R−r⎞n = ⎜ ⎟ = ⎜ ⎟ 

umax ⎝R⎠ ⎝ R ⎠ 

gdje je y udaljenost od stijenke cijevi, a r cilindarska koordinata (udaljenost od simetrale 

sr 

cijevi), R polumjer cijevi, a parametar n zavisi od Reynoldsova broja 

uD ρ 

Re = . prosječna 

μ 

brzina po presjeku cijevi je po definiciji


1 

sr = ∫ d 

A 

= 

R 

⎛ 

2 max 

π ∫ ⎜ 

0 ⎝ 

− n ⎞ 

⎟ 2 πd 

⎠ 

= max 

2 

1 1 R r 2n 

u u A u r r u 

A R R n n 

( + 1)( 2 + 1) 

Sljedeća tablica prikazuje vrijednosti parametra n i odgovarajuću vrijednost srednje brzine, 

za različite Reynoldsove brojeve 

Re= 

3 

4.0⋅ 10 

4 

2.3⋅ 10 

5 

1.1⋅ 10 

6 

1.1⋅ 10 

6 

2.0⋅ 10 

6 

3.2⋅ 10 

n= 6 6.6 7 8.8 10 10 

u / u = 0.791 0.807 0.817 0.850 0.865 0.865 

sr max 

Iz tablice se vidi da se povećanjem Reynoldsova broja prosječna vrijednost brzine po presjeku 

približava maksimalnoj brzini, jer se povećanjem Reynoldsova broja povećava i turbulentna 

viskoznost. 

Blasiusov empirički izraz za faktor trenja, koji vrijedi u području Reynoldsova broja do 

1 

− 

⎛u 4 

srD⎞ 

= 0.3164 = 

80 

5 

10 je 

0.3164 

λ ⎜ ⎟ 

0.25 

⎝ υ ⎠ Re 

5 

Prema gornjoj tablici u području Reynoldsova broja do 10 približno vrijedi usr ≈ 0.8umax, 

te 

primjenom Blasiusove formule, prethodno izvedeni izraz za smično naprezanje možemo 

pisati 

1 

w 

2 

usr 1 

0.3164 

0.8u 4 

max 2R 

⎟ 

2 

( 0.8umax) 0.0225 

2 

umax 

τ 

λ 

= ρ 

8 

= 

8 

⎛ 

⎜ 

⎜⎝ ⎜ 

υ 

− 

⎞ 

⎠⎟⎟ ρ = ρ 

⎛ υ ⎞ 

⎜ 

⎟ 

⎜ ⎜umaxR⎟ 

⎟ 

⎝ ⎠ 

2 

Uzimajući da je po definiciji τw= ρvτ, 

iz gornjeg izraza slijedi veza 

⎛vR⎞ τ 

umax = 8.74v 

⎜ ⎟ 

τ ⎜⎜⎝ ⎟ 

υ ⎠ ⎟ 

što uvršteno u izraz za profil brzine uz n = 7 daje 

u ⎛vτy⎞ = 8.74⎜ 

⎟ 

v υ 

τ 

1 

7 

1 

7 

⎝ ⎠ ili ( ) 1 

+ + 

u = 8.74 y 7 

1 

7 

u ⎛ y ⎞ 

Dakle izraz = ⎜ ⎟ za profil brzine u hidraulički glatkoj cijevi pri Reynoldsovu broju 

umax ⎝R⎠ 5 

10 smo uz pomoć Blasiusova izraza za faktor trenja prikazali u bezdimenzijskim 

varijablama, definiranima uz izvod logaritmičkog zakona, pa se sada ti profili brzine mogu 

prikazati u istom dijagramu zajedno s rezultatima mjerenja. Takav dijagram upravo prikazuje 

sljedeća slika, na kojoj su kružićima označeni rezultati mjerenja pri različitim vrijednostima 

Reynoldsova broja. Očito je da svi mjerni rezultati približno padaju na jednu krivulju, što 

potvrđuje činjenicu da tako prikazani rezultati ne zavise od Reynoldsova broja. U istom je 

dijagramu ucrtan linearni profil brzine iz viskoznog podsloja (s obzirom da je na apscisi 

dekadski logaritam y + ovdje je do krivulja 1), logaritmički profil brzine (definiran s κ = 0.4 i 

B = 5.5 - pravac 3), te prijelazno područje između viskoznog podsloja (linearnog profila) i 

inercijalnog podsloja (logaritmičkog profila). Krivuljom 4 je označen gore dobiveni izraz iz 

Blasiusove formule i n = 7 , a krivuljom 5 analogni izraz koji se dobije iz pretpostavke n = 10 

koja odgovara višim vrijednostima Reynoldsova broja. Iz slike je jasno da linearni profil 

vrijedi neposredno uz stijenku cijevi, za 5 log y 0.7 

+ < ), a logaritmički profil brzine 

y + < ( ( ) 

1 

4


počinje vrijediti za log( y ) 1.5 

+ > ( y 31 

+ > ). Također je uočljivo puno bolje slaganje 

logaritmičkog profila brzine s rezultatima mjerenja, od profila brzine dobivenih uz 

pretpostavke n = 7 i n = 10 (krivulje 4 i 5). Krivulja 4 se bolje slaže s mjerenjima u području 

bliže stijenci, a krivulja 5 dalje od stijenke. 

u 

+ = 

Profil brzine u hidraulički glatkim cijevima 

+ + 

+ 

1- viskozni podsloj u = y ; 2- prijelazni podsloj; 3 – inercijalni podsloj u 

+ ( y ) 

4- ( ) 1/7 

+ 

u = 

+ 

y ; 5 - ( ) 1/10 

+ 

u = 

+ 

y 

8.74 

u 

v τ 

Profil brzine ( ) 1/7 

+ + 

u y 

11.5 

81 

= 2.5ln + 5.5 

= 8.74 smo dakle dobili uz pretpostavku Blasiusova zakona za faktor 

trenja, a taj se profil lošije slaže s mjerenjima nego logaritmički profil, pa se nameće ideja da 

se krene od pretpostavke da logaritmički profil vrijedi po čitavom presjeku cijevi, pa da se iz 

te pretpostavke odredi zakon faktora trenja (tako dobiveni zakon nosi naziv Prandtlov 

univerzalni zakon faktora trenja). 

Dakle polazimo od pretpostavki da je profil zadan izrazom 

+ + 

u = 2.5ln ( y ) + 5.5 , 

odnosno 

⎡ ⎛vτ( R−r) ⎞ ⎤ 

u = vτ⎢2.5ln ⎜ ⎟+ 

5.5 

υ 

⎥ 

⎣ ⎝ ⎠ ⎦ , 

λ 

a vrijedi i prije izvedeni izraz vτ= usr 

. 

8 

Srednja brzina je po definiciji 

R 

1 ⎡ ⎛vτ( R−r) ⎞ ⎤ 

usr = v 2.5ln 5.5 2r dr 

2 τ 

π 

R π ∫ ⎢ ⎜ + 

υ 

⎟ ⎥ , 

0 ⎣ ⎝ ⎠ ⎦ 

Re 

log( ) log yv 

+ ⎛ τ ⎞ 

y = ⎜ ⎟ 

⎝ ν ⎠

a nakon integracije 1 se dobije 

⎛ ⎛vR τ ⎞ ⎞ 

usr = vτ⎜2.5ln 

⎜ + 4.25⎟ 

υ 

⎟ 

⎝ ⎝ ⎠ ⎠ 


λ 

Uvrštavanjem izraza vτ= usr 

u gornji izraz, dobije se 

8 

8 ⎛ ⎛ λ usr 2R⎞ 

⎞ 

= ⎜2.5ln + 4.25 

λ ⎜ 

⎜ ⎟ ⎟ 

8 2υ 

⎟ 

, 

⎟ 

⎝ ⎝ ⎠ ⎠ 

ili nakon sređivanja i prijelaza s prirodnog na dekadski logaritam 

1 

= 2.03log( Re λ ) − 0.91 

λ 

Naravno da koeficijenti u gornjem izrazu neće biti točni, jer logaritmički profil ne vrijedi u 

neposrednoj blizini stijenke i pri simetrali cijevi. Značaj dobivenog rezultata sastoji se u tome 

da smo dobili oblik zakona u kojem se koeficijenti određuju metodom najmanjih kvadrata na 

temelju rezultata mjerenja. Nakon takve korekcije koeficijenata Prandtlov univerzalni zakon 

za faktor trenja u strujanju kroz hidraulički glatke cijevi, poprima konačan oblik 

1 

= 2.0log( Re λ ) − 0.8 

λ 

Ovaj zakon je primjenjiv na cijelo područje vrijednosti Reynoldsovih brojeva koji se 

pojavljuje u praksi. 

Strujanje kroz hidraulički hrapave cijevi 

U tehničkoj praksi su cijevi uglavnom hrapave, a osnovni problem je u tome što se hrapavost 

opisuje s puno parametara, npr. visina hrapavosti, oblik hrapavosti, raspored hrapavosti, 

gustoća hrapavosti (broj neravnina po jedinici površine) i sl. Sustavno ispitivanje strujanja u 

umjetno ohrapavljenim cijevima izvršio je Nikuradse, tako da je na stijenku cijevi lijepio 

zrnca pijeska određenog promjera i to maksimalno gusto, tako da mu je jedini parametar koji 

opisuje hrapavost bila promjer zrnaca pijeska, što ćemo zvati visinom pješčane hrapavosti k s . 

Sljedeća slika prikazuje dijagram s njegovim rezultatima mjerenja u umjetno ohrapavljenim 

cijevima, gdje je na apscisi Reynoldsov broj, a na ordinati stostruka vrijednost faktora trenja 

(obje veličine u logaritamskom mjerilu). Pravcem 1, definiran je zakon promjene faktora 

trenja u laminarnom strujanju (potvrđeno je analitičko rješenje prema kojemu je λ = 64/ Re ). 

Krivulja 2 označuje Blasuiusov zakon faktora trenja za hidraulički glatke cijevi, koji vrijedi za 

5 

Reynoldsove brojeve do 10 , krivulja 3 označuje Prandtlov univerzalni zakon faktora trenja 

za strujanje u hidraulički glatkim cijevima. 

Iz prikazanih rezultata moguće je zaključiti sljedeće: 

1) hrapavost stijenke nema utjecaja u laminarnom strujanju ( λ = 64/ Re za bilo koju 

hrapavost stijenke). 

⎡ ⎤ 

u = v 2.5ln + 5.5 2r dr = ⎢2.5 rln dr+ 5.5rdr⎥= ⎣ ⎦ ⎣ ⎦ 

sr 

R 

1 ⎡ 

2 τ 

R π∫ ⎢ 

0 

⎛vτ( R−r) ⎞ 

⎜ ⎟ 

⎝ υ ⎠ 

⎤ 

⎥ π 

2 vτ 2 

R 

R 

∫ 

0 

⎛vτ( R−r) ⎞ 

⎜ ⎟ 

⎝ υ ⎠ 

R 

∫ 

0 

2v ⎡2.5⎛ 2 

= r 2 ⎢ ⎜ 

R ⎣ 2 ⎝ 

⎛v ⎞ 

⎜ ⎟+ 

⎝υ⎠ 2 2 

r −R R−r R 

2 

2Rr+ r ⎞ 5.5 ⎤ 2 

− ⎟+ 

r ⎥ = 

2 ⎠ 2 ⎦0 

2 

2v 

⎛ ⎛ τ 2 ⎛vτ ⎞ R 2 ⎞ 5.5 ⎞ 2 ⎛ ⎛vR τ ⎞ ⎞ 

= 1.25 R ln − + R ln R R v 2.5ln 4.25 

2 ⎜ + ⎟= 

τ 

+ 

1 τ τ ln ( ) ln ( ) 

R ⎜ ⎜ ⎜ ⎟ 

⎟ ⎜ ⎜ ⎟ ⎟ 

⎝υ⎠ 2 

2 ⎟ 

⎝ ⎝ ⎠ ⎠ 

⎝ ⎝ υ ⎠ ⎠ 

82


2) Faktor trenja (a time i gubitak visine energije) je veći u hrapavim nego u hidraulički 

glatkoj cijevi. Kod relativno malih visina hrapavosti, pri niskim vrijednostima 

Reynoldsova broja hrapavost se ne manifestira (faktor trenja je jednak onome za 

hidraulički glatke cijevi. 

3) Pri visokim vrijednostima Reynoldsova broja i najglađe cijevi počinju pokazivati 

hidrauličku hrapavost. 

4) Za zadanu visinu hrapavosti se može uočiti područje u kojem faktor trenja ne zavisi od 

Reynoldsova broja (područje potpuno izražene hrapavosti). Područje između 

hidraulički glatkog područja i područja potpuno izražene hrapavosti se naziva 

prijelaznim područjem i u njemu je faktor trenja funkcija i Reynoldsova broja i 

relativne visine hrapavosti. 

Ispitivanje Nikuradsea u umjetno ohrapavljenim cijevima (ks=visina pješčane hrapavosti) 

1- laminarno strujanje λ = 64 /Re 

0.25 

2- Blasiusov zakon za hidraulički glatke cijevi λ = 0.3164/ Re 

1 

= 2.0log Re − 0.8 

λ 

3- Prandtlov univerzalni zakon za hidraulički glatke cijevi ( λ ) 

u 

u 

max 

Hrapavost 

y 

R 

83 

Lijeva slika prikazuje profile brzine za tri 

visine hrapavosti, pri Reynoldsovom broju 

6 

Re = 10 . Što je visina pješčane hrapavosti 

veća to će razlika prosječne brzine po 

presjeku i maksimalne brzine veća.


Mjerenja profila brzine u području potpuno izražene hrapavosti pokazuju da ponovo 

vrijedi logaritmički zakon u kojem je y + definiran kao bezdimenzijska udaljenost od 

stijenke, ali normirana s visinom pješčane hrapavosti (umjesto karakterističnom duljinom 

υ / vτ koja je definirana u viskoznom podsloju uz hidraulički glatku stijenku), tako da je 

+ + 

kod hrapavih cijevi y = y/ ks(umjesto 

y = vτy/ υ ). Sljedeća slika prikazuje dijagram s 

rezultatima mjerenja brzine (prikazano u bezdimenzijskim varijablama), pri čemu je y + u 

logaritamskom mjerilu. 

u 

+ = 

u 

v τ 

y 

log = 

log y 

k 

Zakon promjene brzine izražava se izrazom 

u ⎛ y ⎞ ⎛ y ⎞ 

= 5.75log ⎜ ⎟+ 8.5 = 2.5ln ⎜ ⎟+ 

8.5 

vτ⎝ks ⎠ ⎝ks ⎠ 

Ovaj izraz vrijedi u području potpuno izražene turbulencije, tj. u području kada faktor 

trenja više ne zavisi od Reynoldsova broja. Fizikalno je jasno da kada visina hrapavosti 

teži k nuli, da hidraulički hrapava stijenka postaje hidraulički glatka, pa bi i gornji zakon 

morao prijeći u zakon za hidraulički glatke cijevi, koji glasi 

u ⎛vτy⎞ ⎛vτy⎞ 1 ⎛vτy⎞ = 5.75log ⎜ ⎟+ 5.5 = 2.5ln ⎜ ⎟+ 5.5 = ln ⎜ ⎟+ 

B 

vτ 

⎝ υ ⎠ ⎝ υ ⎠ κ ⎝ υ ⎠ 

To znači da se i logaritmički zakon za hidraulički glatke cijevi mora moći prikazati s 

pomoću zakona za hidraulički hrapave cijevi. Ako se u gornjem izrazu doda i oduzme član 

ln k s , on će prijeći u oblik 

u ⎛ y ⎞ ⎛vτks ⎞ ⎛ y ⎞ 

⎛vτks ⎞ 

= 5.75log ⎜ ⎟+ 5.5 + 5.75log ⎜ ⎟= 2.5ln ⎜ ⎟+ 

5.5 + 2.5ln ⎜ ⎟ 

vτ⎝ks ⎠ �� ⎝ υ ⎠ ⎝ks ⎠ �� ⎝ υ ⎠ 

B B 

Prema tome zakon promjene brzine za hrapave cijevi u području potpuno izražene 

hrapavosti i za hidraulički glatke cijevi može se izraziti istim izrazom 

s 

+ 

84

B 


u ⎛ y ⎞ ⎛ y ⎞ 

= 5.75log ⎜ ⎟+ B = 2.5ln ⎜ ⎟+ 

B 

vτ⎝ks ⎠ ⎝ks ⎠ 

gdje je za hrapave cijevi u području potpuno izražene hrapavosti B = 8.5 = konst. , a za 

hidraulički glatke cijevi B postaje funkcija 

⎛vk τ s ⎞ ⎛vk τ s ⎞ 

B = 5.5 + 5.75log⎜ ⎟= 5.5 + 2.5ln ⎜ ⎟ 

⎝ υ ⎠ ⎝ υ ⎠ 

Sljedeći dijagram prikazuje rezultate mjerenja koeficijenta B u funkciji bezdimenzijske 

+ vk τ s 

hrapavosti k = (u logaritamskoj skali). 

υ 

1) Pravac označen s 1, je tangenta na mjerne podatke, a njegova jednadžba upravo 

odgovara zakonu promjene koeficijenta B za hidraulički glatke cijevi. Iz 

dijagrama je vidljivo da se mjerni podaci dobro slažu s tim pravcem do 

⎛kvτ ⎞ kvτ 0.7 

log⎜ ⎟< 

0.7 , odnosno < 10 = 5.01. 

Prema tome površina cijevi neće 

⎝ ν ⎠ 

ν 

+ kvτ 

izražavati hidrauličku hrapavost ako je k = < 5 . S obzirom da je na granici 

ν 

viskoznog podsloja y 5 

+ log( ) log 

= , mogli bi reći da se hrapavost neće manifestirati ako se 

nalazi u viskoznom podsloju. 

2) Horizontalni pravac označen s 2, govori o konstantnoj vrijednosti koeficijenta 

B = 8.5 i odnosi se na područje potpuno izražene hrapavosti, u kojem faktor trenja 

nije funkcija Reynoldsova broja. Iz dijagrama se dade očitati da je u tom području 

+ kvτ 

približno k = > 70 . 

ν 

kvτ 3) Za 5< < 70 govorimo o prijelaznom području turbulentnog strujanja u 

ν 

hrapavim cijevima u kojima je faktor trenja funkcija i Reynoldsova broja i 

relativne visine hrapavosti. 

kv 

+ ⎛ τ ⎞ 

k = ⎜ ⎟ 

⎝ ν ⎠ 

85


Valja naglasiti da se prikazani rezultati odnose na umjetnu pješčanu hrapavost. Stvarna 

hrapavost se opisuje s puno više parametara, a zavisi od materijala cijevi, tehnologije izrade 

cijevi, stanja zaprljanosti (npr. pri transportu nafte, teže frakcije se talože na površinu cijevi) i 

starosti površine (npr. korozija cijevi povećava hrapavost). Za praktične proračune načinjen je 

Moodyjev dijagram u kojem se definira ekvivalentna pješčana hrapavost, kao ona visina 

pješčane hrapavosti koja daje faktor trenja jednak onome u stvarno hrapavoj cijevi. 

Turbulentno optjecanje hidraulički glatke i hrapave ploče 

Jedno od korisnih rješenja za inženjersku praksu, je i rješenje turbulentnog graničnog sloja uz 

ravnu ploču. Dakako da u rješavanju praktičnih problema rijetko imamo optjecanje ravne 

ploče, ali sila otpora ravne ploče nam određuje donju vrijednost te sile ispod koje se ne može 

ići. Tako se npr. za inženjersku procjenu sile otpora broda koristi vrijednost sile otpora 

ekvivalentne ravne ploče (koja je površine jednake površini broda) pomnoženoj s faktorom 

forme, kojim se uzima u obzir i dio sile otpora oblika. Taj se faktor npr. uzima iskustveno, na 

temelju poznavanja podataka na sličnim formama. 

Naravno, čim se radi o turbulentnom strujanju ne postoji analitičko rješenje problema 

optjecanja ravne ploče, koje doduše nismo dobili niti u slučaju laminarnog strujanja (iako neki 

Blasiusovo rješenje svrstavaju u klasu analitičkih rješenja, budući se ono može odrediti po 

volji točno), već u obzir dolazi samo numeričko rješavanje i to uglavnom vremenski 

osrednjenih (Reynoldsovih) jednadžbi ili pojednostavljene von Kármánove integralne 

jednadžbe. Von Kármánova jednadžba za turbulentno strujanje je istog oblika kao i za 

laminarno strujanje s razlikom da se u njoj pojavljuju vremenski osrednjene veličine. 

Najčešće korištena rješenja von Kármánove jednadžbe su ona koja se dobiju pretpostavkom 

profila brzine oblika 

1 

u ⎛y⎞n = ⎜ 

⎟ 

v ⎜⎝ 

⎟ 

δ δ ⎠ ⎟ 

, 

(to je analogija s profilom brzine u cijevima, gdje brzina u max u simetrali cijevi prelazi u 

vremenski osrednjenu brzinu na rubu graničnog sloja, a polumjer cijevi R u vremenski 

osrednjenu debljinu graničnog sloja). Vrijednost parametra n zavisna je od Reynoldsova 

broja na izlaznom rubu ploče Re= ρv∞L/ μ, 

a vrijednost n raste s porastom Reynoldsova 

broja. Ako je n = 7 govori se o Prandtlovom zakonu jedne sedmine, a za n = 11 o zakonu 

5 7 

jedne jedanaestine. Zakon 1/7 se koristi u području 510 ⋅

1000 CD 


1 

− 

7 

⎛v x⎞ 

∞ 

τw( x) = 0.0526 ⎜ 

⎟ ρv 

⎜⎝ υ ⎠⎟ 

2 

∞ 

, i 

C 

D 

⎛v L⎞ 

∞ 

= 0.0307 ⎜ 

⎟ 

⎜⎝ 

⎟ 

υ ⎠⎟ 

Osim ovih izraza u upotrebi su i Prandtl-Schlichtingov izraz 

1 

− 

7 

C 

. 

( ) 258 

log Re 

87 

0. 455 

= , koji se temelji 

D . 

na rješavanju von Kármánove jednadžbe uz pretpostavku logaritmičkog profila brzine u 

graničnom sloju, te još neke empiričke formule. Sljedeći dijagram prikazuje rezultate 

mjerenja koeficijenta otpora hidraulički glatke ploče (točke označene kružićima) i krivulje 

koje označuju pojedine zakone promjene koeficijenta otpora. 

Značenje pojedinih krivlja na slici je sljedeće: 

Koeficijent otpora hidraulički glatke ploče 

1 - Blasiusovo rješenje za laminarni granični sloj: C 

2 - Prandtlov zakon 1/7: C D 0. 074 Re − 

= 

0. 455 

3 - Prandtl-Schichting: CD 

= 

. 

log Re 

( ) 258 

4 - Schultz-Grunow: ( ) 264 − . 

02 . 

C D = 0. 427 log Re − 0. 407 

D 

1. 328 

= 

Re 

Krivulja 3a prikazuje prijelazno područje. Naime na početku hidraulički glatke ploče prvo se 

formira laminarni granični sloja, a nakon kritičnog Reynoldsova broja (Rekr=3·10 5 do 30·10 5 ) 

počinje prelaziti u turbulentni granični sloj. Zbog početnog dijela laminarnog graničnog sloja 

uvodi se korekcija (smanjenje koeficijenta otpora dobivenog uz pretpostavku da se turbulentni 

granični sloj razvija od početka ploče) u obliku A/ Re, gdje je A parametar koji ovisi o 

kritičnom Reynoldsovom broju. Što je Rekr veći to će područje laminarnog graničnog sloja 

biti veće, pa će i korekcija (smanjenje) koeficijenta otpora biti veće. Sljedeća tablica prikazuje 

vrijednosti parametra A u zavisnosti od Rekr 

Rekr 3·10 5 5·10 5 10·10 5 30·10 5 

A 1050 1700 3300 8700 

U∞L Re = 

ν


Korekciju ima smisla primjenjivati kada je Reynoldsov broj na temelju duljine ploče relativno 

5 7 

8 

6 

mali (u području 510 ⋅ < Re < 10). 

Ako je npr. Re = 10 , a kritični Reynoldsov broj 10 , 

tada će laminarni granični sloj zauzimati svega jedan posto duljine ploče, što je naravno s 

inženjerskog stajališta zanemarivo. Korekcija koeficijenta otpora se može vršiti ili u zakonu 

1/7 ili u Prandtl-Schlichtingovoj formuli. Krivulja 3a prikazuje korigiranu Prandtl- 

Schlichtingovu formulu, koja dakle glasi 

0. 455 A 

CD 

= − . 

log Re Re 

( ) 258 

Treba naglasiti da se prijelaz laminarnog u turbulentno strujanje može uz pomoć takozvanih 

stimulatora turbulencije pomaknuti u područje nižih Reynoldsovih brojeva. Stimulator 

turbulencije je žica određenog promjera koja se postavlja na ploču poprečno na vektor brzine 

strujanja. Na toj se žici pojavljuju mali vrtlozi koji iniciraju nestabilnost strujanja i prijelaz 

laminarnog u turbulentno strujanje. Ova se tehnika često koristi u bazenskom ispitivanju 

brodskih modela. Za slučaj da se u ispitivanju zadovoljava jednakost Froudeovih brojeva, 

9 

Reynoldsov broj za prototipni brod može biti reda veličine 10 , a na modelu broda reda 

6 

veličine 10 . Strujanje fluida oko prototipnog broda je dobrim dijelom laminarno, pa je jasno 

da ta dva strujanja neće biti slična. Da bi se osigurala što veća sličnost dvaju strujanja na 

pramcu brodskog modela se stavljaju stimulatori turbulencije, kojima je zadatak izazvati što 

raniji prijelaz laminarnoga u turbulentno strujanje, kako bi što veće područje strujanja bilo u 

režimu turbulentnoga strujanja. Naravno da mjesta na koja se stavljaju stimulatori turbulencije 

moraju biti u području dovoljno velikog Reynoldsova broja, jer će u protivnom nestabilnosti 

izazvane stimulatorom turbulencije biti prigušene (govori se o relaminarizaciji turbulencije), 

pa će se prijelaz laminarnog u turbulentno strujanje pojaviti na nekom većem Reynoldsovu 

broju. 

Turbulentno strujanje oko hidraulički hrapave ploče 

1000 CD 

vk ∞ s 

υ 

vL ∞ Re = 

υ 

L 

k 

s 

88


Gornja slika prikazuje dijagram koeficijenta otpora umjetno ohrapavljene ploče duljine L . Na 

dijagramu k s označuje visinu pješčane hrapavosti. Na apscisi je Reynoldsov broj, a na 

ordinati koeficijent otpora pomnožen s 1000. Parametarske krivulje hrapavosti su dane u dva 

vk ∞ s 

L 

oblika: za = konst. 

i za = konst. . Donja krivulja označuje zakon promjene 

υ 

k s 

koeficijenta otpora hidraulički glatke ploče. Slično kao i kod faktora trenja u hidraulički 

hrapavim cijevima povećanjem Reynoldsova broja počinju se manifestirati i manje visine 

L 

6 

pješčane hrapavosti. Tako bi se iz dijagrama moglo očitati da se hrapavost = 210 ⋅ počinje 

k s 

8 

5 

7 

manifestirati kod Re = 210 ⋅ , hrapavost L/k s = 210 ⋅ kod Re = 210 ⋅ , a hrapavost 

4 

5 

L/k s = 210 ⋅ kod Re = 210 ⋅ . Mogli bismo definirati dopuštenu visinu hrapavosti k dop kao 

maksimalnu visinu hrapavosti koja se neće manifestirati u turbulentnom strujanju. Iz rečenog 

bi za dopuštenu visinu hrapavosti vrijedilo 

L Re 

= 

kdop 

100 

Dopuštena visina hrapavosti nam govori do koje se mjere isplati ulagati u poboljšanje 

kvalitete površine. 

L 

Na gornjem se dijagramu može uočiti da krivulje definirane s = konst. desno od crtkane 

k s 

linije postaju horizontalne, što znači da koeficijent otpora prestaje zavisiti od Reynoldsova 

−25 

. 

⎛ L ⎞ 

broja. To je područje potpuno izražene hrapavosti za koje je C D = ⎜189 . + 162log . ⎟ . 

⎝ ks 

⎠ 

Pri optjecanju tijela kod kojih je pretežiti dio sile otpora otpor trenja, hrapavost povećava silu 

otpora i zbog pomicanja kritičnog Reynoldsova broja na niže vrijednosti, čime se smanjuje 

područje laminarnog graničnog sloja. Međutim kod oblih tijela poput cilindra i kugle, uz 

pomoć hrapavosti se može smanjiti koeficijent otpora. Sljedeća slika prikazuje zavisnost 

koeficijenta otpora hidraulički glatkog cilindra i kugle u funkciji Reynoldsova broja. 

Koeficijent otpora dugog cilindra i kugle 

89


Pri niskim vrijednostima Reynoldsova broja (manjim od 1) inercijske sile se mogu zanemariti, 

a koeficijent otpora je oblika C D = konst. / Re. 

Pri visokim vrijednostima Reynoldova broja 

postoji područje Reynoldsova broja u kojem je koeficijent otpora konstantan (sila otpora je 

razmjerna kvadratu brzine). 

Pri određenom Reynoldsovu broju obje krivulje pokazuju gotovo skokovito smanjenje 

koeficijenta otpora, što se naziva «krizom otpora». Ova se pojava objašnjava premještanjem 

točke odvajanja. Sljedeća slika prikazuje turbulentno optjecanje kugle pri 

4 

Re = ρv∞D/ μ = 1.5⋅ 10 . Strujanje u graničnom sloju do točke odvajanja strujanja je 

laminarno, a do odvajanja je došlo jer je fluidu ponestalo kinetičke energije za svladavanje 

pozitivnog gradijenta tlaka. 

Optjecanje kugle pri 

Optjecanje kugle pri 

4 

Re = 1.5⋅ 10 

4 

Re = 310 ⋅ s ugrađenim turbulizatorom 

4 

Gornja slika prikazuje optjecanje kugle pri Re = 310 ⋅ , u kojem je tranzicija laminarnog u 

turbulentno strujanje izazvana turbulizatorom (žičanim prstenom) iza kojeg se jasno vidi da je 

laminarno strujanje prešlo u režim turbulentnog strujanja. U turbulentnom graničnom sloju se 

90


kinetička energija vanjskog strujanja pretvara u kinetičku energiju turbulentnih pulzacija 

unutar graničnog sloja, tako da fluid ima energije za svladavanje pozitivnog tlaka u 

graničnom sloju, te se točka zastoja pomiče prema stražnjoj točki zastoja. Pomicanjem točke 

odvajanja slika tlaka se mijenja u smislu smanjivanja otpora oblika, čime dolazi do značajnog 

smanjenja koeficijenta otpora. Dakle bez turbulizatora bi do krize otpora došlo pri 

5 

Reynoldsovom broju iznad 10 , a uz pomoć turbulizatora (hrapavosti) vrijednost 

Reynoldsova broja pri kojem se postiže kriza otpora, se može smanjiti. Sljedeći dijagram 

prikazuje koeficijent otpora različito hrapavih kugli i to u blizini kritičnog Reynoldsova broja. 

Iz dijagrama je očito da za određeno područje Reynoldsova broja hrapava kugla ima manji 

koeficijent otpora nego hidraulički glatka kugla. 

91

v - FSB

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?