Emmanuel Amiot Modèles algébriques et algorithmes pour la ...

12
10
8
6
4
2
4
0
ME7,3
4
alternative title 11
2
12
10
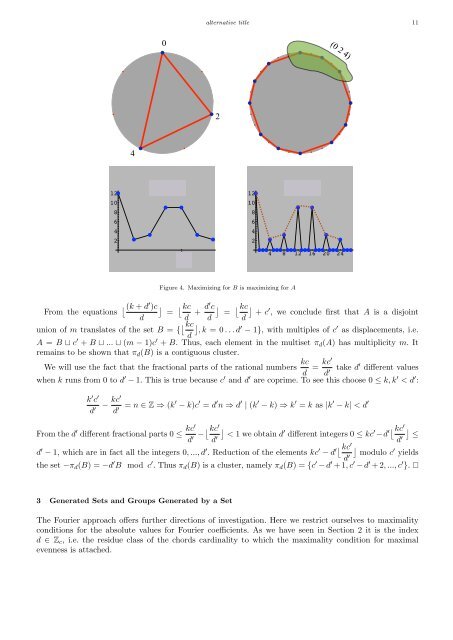
Figure 4. Maximizing for B is maximizing for A
8
6
4
2
ME28,12
(0 2 4)
4 8 12 16 20 24
From the equations (k + d ′ )c
kc
=
d d + d′ c
kc
= + c ′ , we conclude first that A is a disjoint
d d
union of m translates of the set B = { kc
, k = 0 . . . d ′ − 1}, with multiples of c ′ as displacements, i.e.
d
A = B ⊔ c ′ + B ⊔ ... ⊔ (m − 1)c ′ + B. Thus, each element in the multiset πd(A) has multiplicity m. It
remains to be shown that πd(B) is a contiguous cluster.
We will use the fact that the fractional parts of the rational numbers kc
d
= kc′
d ′ take d′ different values
when k runs from 0 to d ′ − 1. This is true because c ′ and d ′ are coprime. To see this choose 0 ≤ k, k ′ < d ′ :
k ′ c ′ kc′
−
d ′ d ′ = n ∈ Z ⇒ (k′ − k)c ′ = d ′ n ⇒ d ′ | (k ′ − k) ⇒ k ′ = k as |k ′ − k| < d ′
From the d ′ different fractional parts 0 ≤ kc′ ′
−kc
d ′ d ′
kc ′
< 1 we obtain d ′ different integers 0 ≤ kc ′ −d ′
d ′
≤
d ′ − 1, which are in fact all the integers 0, ..., d ′ . Reduction of the elements kc ′ ′
− d ′kc
d ′
modulo c ′ yields
the set −πd(B) = −d ′ B mod c ′ . Thus πd(B) is a cluster, namely πd(B) = {c ′ − d ′ + 1, c ′ − d ′ + 2, ..., c ′ }.
3 Generated Sets and Groups Generated by a Set
The Fourier approach offers further directions of investigation. Here we restrict ourselves to maximality
conditions for the absolute values for Fourier coefficients. As we have seen in Section 2 it is the index
d ∈ Zc, i.e. the residue class of the chords cardinality to which the maximality condition for maximal
evenness is attached.