Emmanuel Amiot Modèles algébriques et algorithmes pour la ...

3
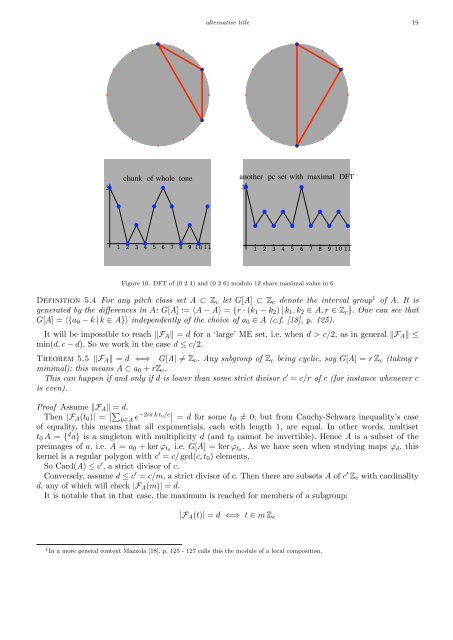
chunk of whole tone
1 2 3 4 5 6 7 8 9 10 11
alternative title 19
another pc set with maximal DFT
3
1 2 3 4 5 6 7 8 9 10 11
Figure 10. DFT of (0 2 4) and (0 2 6) modulo 12 share maximal value in 6
Definition 5.4 For any pitch class set A ⊂ Zc let G[A] ⊂ Zc denote the interval group 1 of A. It is
generated by the differences in A: G[A] := 〈A − A〉 = {r · (k1 − k2) | k1, k2 ∈ A, r ∈ Zc}. One can see that
G[A] = 〈{a0 − k | k ∈ A}〉 independently of the choice of a0 ∈ A (c.f. [18], p. 125).
It will be impossible to reach FA = d for a ‘large’ ME set, i.e. when d > c/2, as in general FA ≤
min(d, c − d). So we work in the case d ≤ c/2.
Theorem 5.5 FA = d ⇐⇒ G[A] = Zc. Any subgroup of Zc being cyclic, say G[A] = r Zc (taking r
minimal); this means A ⊂ a0 + rZc.
This can happen if and only if d is lower than some strict divisor c ′ = c/r of c (for instance whenever c
is even).
Proof Assume FA = d.
Then |FA(t0)| =
k∈A e−2iπ k t0/c = d for some t0 = 0; but from Cauchy-Schwarz inequality’s case
of equality, this means that all exponentials, each with length 1, are equal. In other words, multiset
t0 A = { d a} is a singleton with multiplicity d (and t0 cannot be invertible). Hence A is a subset of the
preimages of a, i.e. A = a0 + ker ϕt0 i.e. G[A] = ker ϕt0. As we have seen when studying maps ϕd, this
kernel is a regular polygon with c ′ = c/ gcd(c, t0) elements.
So Card(A) ≤ c ′ , a strict divisor of c.
Conversely, assume d ≤ c ′ = c/m, a strict divisor of c. Then there are subsets A of c ′ Zc with cardinality
d, any of which will check |FA(m)| = d.
It is notable that in that case, the maximum is reached for members of a subgroup:
|FA(t)| = d ⇐⇒ t ∈ m Zc
1 In a more general context Mazzola [18], p. 125 - 127 calls this the module of a local composition.