Magnetic Fields and Magnetic Diagnostics for Tokamak Plasmas

Magnetic fields and tokamak plasmas
Alan Wootton
The “self inductance per unit length” is expressed as
1
∫( ( ) 1+α
)
l i
= 2 1 − 1 − x 2
0
2
dx
x
6.36
The solution is written in terms of PolyGamma and EulerGamma functions:
l i = EulerGamma + 2 PolyGamma[0, 2 + α] - PolyGamma[0, 3 + 2 α]
6.37
However, a polynomial fit in α can also be used:
l i = 0.509619 + 0.462798α − 0.0630876α 2 + 0. 00443746α 3 6.38
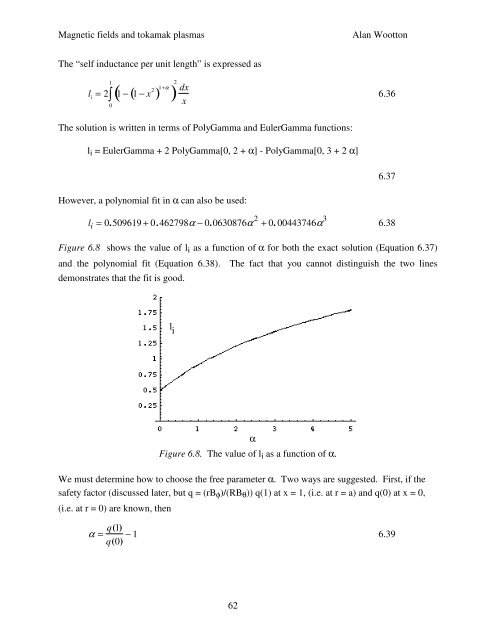
Figure 6.8 shows the value of l i as a function of α for both the exact solution (Equation 6.37)
and the polynomial fit (Equation 6.38). The fact that you cannot distinguish the two lines
demonstrates that the fit is good.
l i
Figure 6.8. The value of l i as a function of α.
We must determine how to choose the free parameter α. Two ways are suggested. First, if the
safety factor (discussed later, but q = (rB φ )/(RB θ )) q(1) at x = 1, (i.e. at r = a) and q(0) at x = 0,
(i.e. at r = 0) are known, then
α = q(1)
q(0) − 1 6.39
α
62