TPF-I SWG Report - Exoplanet Exploration Program - NASA

D ESIGN AND A R C H I T E C T U R E T RADE S TUDIES
a) az = 30 deg b)
5 x 1013
5 x 1013
4.5
4
planet
signal
instability
noise
Cubic fit
4.5
4
f / Hz
3.5
3
2.5
2
Quadratic
fit
1.5
1.5
-0.4 -0.2 0 0.2 0.4 0.6
-0.4 -0.2 0 0.2 0.4 0.6
photon rate / s -1 photon rate / s -1
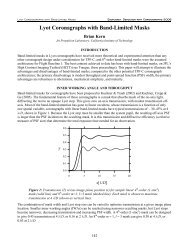
Figure 4-19. (a) Vertical cuts through wavelength-azimuth plots of Fig. 4-18 d and f at an azimuth of
30 degrees. Planet signal shows characteristic oscillatory behavior. Instability noise follows low-order
polynomial dependence, with independent contributions to the two halves of the spectrum (separate
hardware). (b) Result of removing low-order fits. Most of the planet signal remains, but the instability
noise is almost completely removed.
has both positive (white) and negative (black) regions. A single planet is shown with a radial offset of 50
mas (2.5 × 10 -7 rad) from the star. The detected photon rate from the planet as a function of rotation
azimuth of the array is shown in Fig. 4-18c. The circular symbol gives the photon rate for the rotation
angle shown in Fig. 4-18b. The peaks and valleys of Fig. 4-18c correspond to the white and black parts of
the response along the circular locus in Fig. 4-18b. As the wavelength is increased from 10 μm, the
instrument response of Fig. 4-18b is scaled about the center, with increased spacing between the peaks
and valleys of the response. The photon rate from the planet is also changed according to its spectral
distribution. Figure 4-18d combines these effects to show how the planet photon rate depends on both the
wavelength (or optical frequency) and the array rotation azimuth. The example is based on a planet with a
265-K black-body spectrum, which has a substantially higher photon rate at 20 μm compared to 6 μm. A
horizontal section through this distribution at a wavelength of 10 μm gives the profile shown in Fig. 4-
18c. The wavelength-azimuth plot is a convenient representation of the data obtained from spectral
channels of TPF-I as the array is rotated.
In addition to the planet signal, there are two distinct classes of noise (Section 4.2.1). The photon (shot)
noise is shown in Fig. 4-18e, and is proportional to the square root of the overall photon rate. Important
contributors are the local and exozodiacal backgrounds and stellar leakage. The instrument instability
noise is shown in Fig. 4-18f. We assume that the full spectral range of 6 to 20 μm has been split for
practical reasons into two bands for nulling: 6–10 μm and 10–20 μm. (It is difficult to cover the full range
with one set of glasses and single-mode spatial filters.) Over each of these bands the instability noise at
any instant is represented by a low-order polynomial series in the optical frequency multiplied by the
stellar spectrum, according to Eq. 1. The coefficients vary randomly with time as the instabilities (path
length, tilt, etc.) evolve. In Fig. 4-18f we show instability noise that is random from one azimuth to the
next and from one band to the other (i.e., having a white noise spectrum). In practice the spectrum is not
exactly white, and there will be some correlation, both with azimuth and between the spectral bands, but
we will not rely on this correlation for the analysis presented here. In general, the instability noise
increases at high optical frequencies / short wavelengths. The smooth variation with wavelength, coupled
with the white-noise spectrum in azimuth, result in the distinctive vertical striping seen in the plot.
f / Hz
3.5
3
2.5
2
81