Directional Recording of Swell from Distant Storms - Department of ...

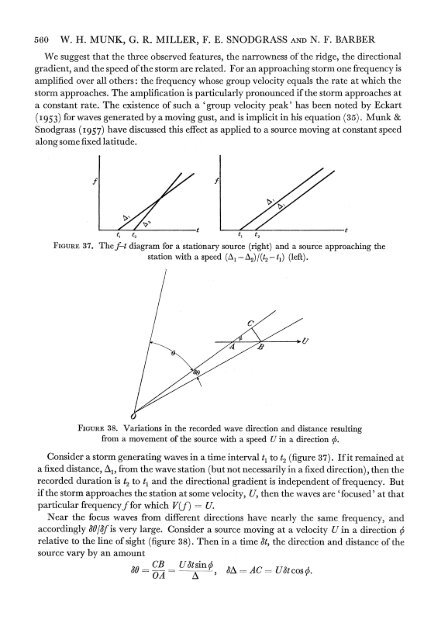
560 W. H. MUNK, G. R. MILLER, F. E. SNODGRASS AND N. F. BARBERWe suggest that the three observed features, the narrowness of the ridge, the directionalgradient, and the speed of the storm are related. For an approaching storm one frequency isamplified over all others: the frequency whose group velocity equals the rate at which thestorm approaches. The amplification is particularly pronounced if the storm approaches ata constant rate. The existence of such a 'group velocity peak' has been noted by Eckart(I953) for waves generated by a moving gust, and is implicit in his equation (35). Munk &Snodgrass (I957) have discussed this effect as applied to a source moving at constant speedalong some fixed latitude.ftl t2 tl t2FIGURE 37. Thef-t diagram for a stationary source (right) and a source approaching thestation with a speed (A1-A2)/(t2 - tl) (left).00AFIGURE 38. Variations in the recorded wave direction and distance resultingfrom a movement of the source with a speed U in a direction q.Consider a storm generating waves in a time interval t1 to t2 (figure 37). If it remained ata fixed distance, A1, from the wave station (but not necessarily in a fixed direction), then therecorded duration is t2 to t1 and the directional gradient is independent of frequency. Butif the storm approaches the station at some velocity, U, then the waves are 'focused' at thatparticular frequencyf for which V(f) = U.Near the focus waves from different directions have nearly the same frequency, andaccordingly 6O/Sf is very large. Consider a source moving at a velocity U in a direction Srelative to the line of sight (figure 38). Then in a time At, the direction and distance of thesource vary by an amountasCB U&tsinqX &A =ACzzU&tcos03