Measurement of the Jet Energy Scale in the CMS experiment ... - IIHE

More documents

Recommendations

Info

50 CHAPTER 4: Reconstructing and Selecting Physics EventFigure 4.4: Parton distribution functions xf(x) for quarks, antiquarks and gluons inthe proton at Q = 100GeV . These distributions are obtained from a fit to deep inelasticscattering data performed by the CTEQ collaboration (CTEQ6L1) [82].their differential cross section. Matrix Element event generators are the main softwaretools in the procedure of generating events as they are responsible for producing thehard scattering event based on Monte Carlo methods. They provide the leading Feynmandiagrams contributing to the hard process and calculate the invariant amplitudeM for that hard interaction. Although the contributions from higher order correctionsup to Next-to-Leading Order (NLO) in perturbative calculations can also be includedin the Matrix Element methods, only the effects of the dominant terms in the invariantamplitude are usually taken into account. For example, NLO corrections to the hardelementary scattering amplitude is included in a Matrix Element by considering theemission of a hard gluon from the initial or final partonic legs in the Feynman diagrmswhile ignoring the contributions including a loop with a virtual gluons. In this sense,singularities are not present in the Matrix Element generators. MadGraph [83] andALPGEN [84] are two examples of Matrix Element generators which are widely used inthe CMS collaboration.With a Matrix Element generator, at the end one would have events with particles atthe final state which were produced based on the Feynman rules presented in the StandardModel of particle physics. The partons in either initial or final state of an evententail the probability of radiating a gluon q → qg, referred to as Initial State Radiation(ISR) or Final State Radiation (FSR) respectively. The emited gluon is subsequentlydecomposed into either a pair of quark-antiquark g → q¯q or a pair of gluons g → gg.Further the radiated partons entail the possibility of additional radiations resulting ina shower of partons moving along the direction of the shower initiator parton. Thesplitting of a parton to other partons is controled by the DGLAP (Dokshitzer-Gribov-Lipatov-Altarelli-Parisi) equations [85–87]. The dedicated softwares which perform the
CHAPTER 4: Reconstructing and Selecting Physics Event 51parton showering are called Parton Showers. In a Parton Shower approach, the emitedgluon can be radiated collinear with respect to the original parton or be very softwhich would yield mathematical singularities. These kind of singularities are handledby applying a lower cut-off on the appropriate parameters. Some of the multi-purposeevent generators which besides being a physics event generator, include Parton Showerprograms are PYTHIA [88] and HERWIG [89].In order to complement the event generation chain, the output of a Matrix Elementgenerator is interfaced with a Parton Shower program to implement the splitting effectson the produced partons of the generated event. Since Parton Shower algorithms canalso produce hard partons in the final state, it is important to resolve the ambiguitiesthat can arise in the final state configurations. For example, a given event with N+1jets in the final state can be obtained by either a Matrix Element generator with N+1partons in the final state or a Matrix Element generator with N partons in the finalstate where an additional parton is produced during the parton showering. Thereforesome matching algorithms have been developed to perform the matching between jetsof hadrons produced in a Parton Shower program and hard partons produced in a MatrixElement generator so that a probable double counting of events is avoided. TheCKKW algorithm [90, 91] and the MLM algorithm [92, 93] are two important examplesof matching schemes used in the event generation procedure.4.1.3 Detector SimulationThe generated Monte Carlo simulated events provide physically observable particlesonly if they undergo a detector simulation. Equivalently a generated particle is observedwhen it interacts with matter. The simulation of the CMS detector is basedon the GEANT4 package which simulates all possible electromagnetic and hadronicinteractions of particles with matter within a magnetic field. For example, in the caseof a generated electron, the possible interactions result in ionization or radiation. Theemitted photons which present themselves by releasing heat and energy, are collectedin the read-out. This would yield the so called experimental “hits” which are thedeposited energy of the particles while traversing the detector material and constituethe building blocks for the roconstruction of the physics objects. It is worth to mentionthat the same reconstruction algorithms are run on either Monte Carlo simulatedevents or events coming from a real proton-proton collision so that one could make afair comparison between theory and experiment.4.2 The Event TopologyWith either Monte Carlo simulated samples or experimental data, physics objects canbe reconstructed. Electronic signals collected in the read-out of the detector are translatedinto position parameters along the particles trajectory and are used to reconstructthe physics objects and their kinematic properties as described in detail in previouschapter. After the object reconstruction, it is the time to reconstruct the physics eventof interest which is called the signal event hereafter. Any other kind of event with thesame observed final state as the signal but not originating from the pp → t¯t process, is
Page 1:
Vrije Universiteit BrusselFaculteit
Page 5 and 6: IntroductionThe Standard Model of p
Page 7 and 8: Chapter 1The Standard Model of Part
Page 9 and 10: CHAPTER 1: The Standard Model of Pa
Page 19 and 20: Chapter 2The CMS experiment at the
Page 21 and 22: CHAPTER 2: The CMS experiment at th
Page 33 and 34: Chapter 3Object ReconstructionThe e
Page 35 and 36: CHAPTER 3: Object Reconstruction 31
Page 51 and 52: Chapter 4Reconstructing and Selecti
Page 53: CHAPTER 4: Reconstructing and Selec
Page 57 and 58: CHAPTER 4: Reconstructing and Selec
Page 71 and 72: Chapter 5Estimating of the Jet Ener
Page 73 and 74: CHAPTER 5: Estimating of the Jet En
Page 91 and 92: 2χ / ndf18.76 / 7p0 9.492e-08 ±9.
Page 105 and 106:
CHAPTER 5: Estimating of the Jet En
Page 107 and 108:
Page 109 and 110:
Page 111 and 112:
Page 113 and 114:
Page 115 and 116:
Page 117 and 118:
Page 119 and 120:
Page 121 and 122:
Page 123 and 124:
Page 125 and 126:
Page 127 and 128:
Page 129 and 130:
Page 131 and 132:
Chapter 6ConclusionThe Standard Mod
Page 133 and 134:
CHAPTER 6: Conclusion 129The method
Page 135 and 136:
Bibliography[1] M. E. Peskin and D.
Page 137 and 138:
BIBLIOGRAPHY 133[40] The ALICE Coll
Page 139 and 140:
BIBLIOGRAPHY 135[76] The CMS Collab
Page 141 and 142:
SummaryJets appear in the final sta
show all

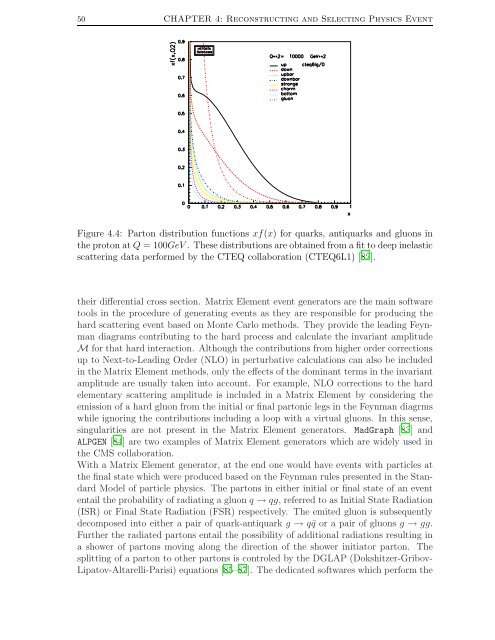
Measurement of the Jet Energy Scale in the CMS experiment ... - IIHE

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?