Measurement of the Jet Energy Scale in the CMS experiment ... - IIHE
Measurement of the Jet Energy Scale in the CMS experiment ... - IIHE
Measurement of the Jet Energy Scale in the CMS experiment ... - IIHE
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
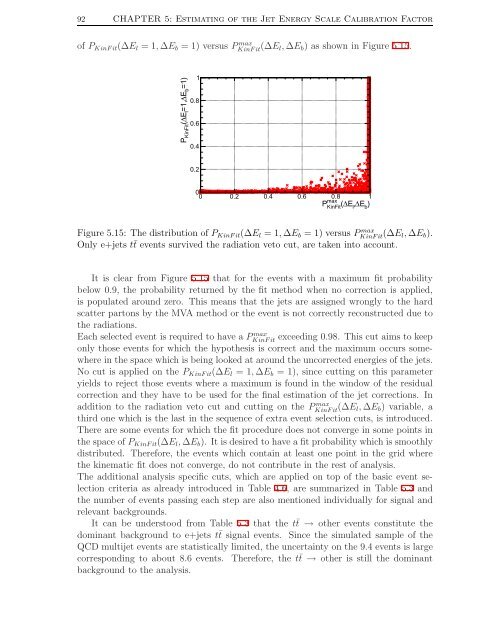
92 CHAPTER 5: Estimat<strong>in</strong>g <strong>of</strong> <strong>the</strong> <strong>Jet</strong> <strong>Energy</strong> <strong>Scale</strong> Calibration Factor<strong>of</strong> P K<strong>in</strong>Fit (∆E l = 1, ∆E b = 1) versus P maxK<strong>in</strong>Fit (∆E l, ∆E b ) as shown <strong>in</strong> Figure 5.15.P K<strong>in</strong>Fit (∆E l =1,∆E b =1)10.80.60.40.200 0.2 0.4 0.6 max0.8 (∆E l,∆E b)1P K<strong>in</strong>FitFigure 5.15: The distribution <strong>of</strong> P K<strong>in</strong>Fit (∆E l = 1, ∆E b = 1) versus P maxK<strong>in</strong>Fit (∆E l, ∆E b ).Only e+jets t¯t events survived <strong>the</strong> radiation veto cut, are taken <strong>in</strong>to account.It is clear from Figure 5.15 that for <strong>the</strong> events with a maximum fit probabilitybelow 0.9, <strong>the</strong> probability returned by <strong>the</strong> fit method when no correction is applied,is populated around zero. This means that <strong>the</strong> jets are assigned wrongly to <strong>the</strong> hardscatter partons by <strong>the</strong> MVA method or <strong>the</strong> event is not correctly reconstructed due to<strong>the</strong> radiations.Each selected event is required to have a PK<strong>in</strong>Fit max exceed<strong>in</strong>g 0.98. This cut aims to keeponly those events for which <strong>the</strong> hypo<strong>the</strong>sis is correct and <strong>the</strong> maximum occurs somewhere<strong>in</strong> <strong>the</strong> space which is be<strong>in</strong>g looked at around <strong>the</strong> uncorrected energies <strong>of</strong> <strong>the</strong> jets.No cut is applied on <strong>the</strong> P K<strong>in</strong>Fit (∆E l = 1, ∆E b = 1), s<strong>in</strong>ce cutt<strong>in</strong>g on this parameteryields to reject those events where a maximum is found <strong>in</strong> <strong>the</strong> w<strong>in</strong>dow <strong>of</strong> <strong>the</strong> residualcorrection and <strong>the</strong>y have to be used for <strong>the</strong> f<strong>in</strong>al estimation <strong>of</strong> <strong>the</strong> jet corrections. Inaddition to <strong>the</strong> radiation veto cut and cutt<strong>in</strong>g on <strong>the</strong> PK<strong>in</strong>Fit max (∆E l, ∆E b ) variable, athird one which is <strong>the</strong> last <strong>in</strong> <strong>the</strong> sequence <strong>of</strong> extra event selection cuts, is <strong>in</strong>troduced.There are some events for which <strong>the</strong> fit procedure does not converge <strong>in</strong> some po<strong>in</strong>ts <strong>in</strong><strong>the</strong> space <strong>of</strong> P K<strong>in</strong>Fit (∆E l , ∆E b ). It is desired to have a fit probability which is smoothlydistributed. Therefore, <strong>the</strong> events which conta<strong>in</strong> at least one po<strong>in</strong>t <strong>in</strong> <strong>the</strong> grid where<strong>the</strong> k<strong>in</strong>ematic fit does not converge, do not contribute <strong>in</strong> <strong>the</strong> rest <strong>of</strong> analysis.The additional analysis specific cuts, which are applied on top <strong>of</strong> <strong>the</strong> basic event selectioncriteria as already <strong>in</strong>troduced <strong>in</strong> Table 4.6, are summarized <strong>in</strong> Table 5.3 and<strong>the</strong> number <strong>of</strong> events pass<strong>in</strong>g each step are also mentioned <strong>in</strong>dividually for signal andrelevant backgrounds.It can be understood from Table 5.3 that <strong>the</strong> t¯t → o<strong>the</strong>r events constitute <strong>the</strong>dom<strong>in</strong>ant background to e+jets t¯t signal events. S<strong>in</strong>ce <strong>the</strong> simulated sample <strong>of</strong> <strong>the</strong>QCD multijet events are statistically limited, <strong>the</strong> uncerta<strong>in</strong>ty on <strong>the</strong> 9.4 events is largecorrespond<strong>in</strong>g to about 8.6 events. Therefore, <strong>the</strong> t¯t → o<strong>the</strong>r is still <strong>the</strong> dom<strong>in</strong>antbackground to <strong>the</strong> analysis.