- Page 2:
This page intentionally left blank
- Page 6:
This is the first comprehensive tex
- Page 10:
cambridge university press Cambridg
- Page 14:
vi An Ode to the Unity of Time and
- Page 18:
viii Contents 4.5 Canonical quantiz
- Page 24:
Preface String theory is one of the
- Page 28:
Preface xiii stein of Caltech for t
- Page 32:
Preface xv NL, NR left- and right-m
- Page 36:
1 Introduction There were two major
- Page 40:
1.2 General features 3 theory fell
- Page 44:
1.2 General features 5 is only cons
- Page 48:
1.3 Basic string theory 7 world she
- Page 52:
1.4 Modern developments in superstr
- Page 56:
1.4 Modern developments in superstr
- Page 60:
1.4 Modern developments in superstr
- Page 64:
1.4 Modern developments in superstr
- Page 68:
2 The bosonic string This chapter i
- Page 72:
2.1 p-brane actions 19 choice of pa
- Page 76:
particle, namely 2.1 p-brane action
- Page 80:
SOLUTION 2.1 p-brane actions 23 The
- Page 84:
where ˙X µ = ∂Xµ ∂τ 2.2 The
- Page 88:
Tαβ, that is, 2.2 The string acti
- Page 92:
2.2 The string action 29 where we h
- Page 96:
2.3 String sigma-model action: the
- Page 100:
2.3 String sigma-model action: the
- Page 104:
2.3 String sigma-model action: the
- Page 108:
2.4 Canonical quantization 37 compo
- Page 112:
2.4 Canonical quantization 39 These
- Page 116:
finds that Eq. (2.85) is solved by
- Page 120:
where N = 2.4 Canonical quantizatio
- Page 124:
In fact, any such state can be reca
- Page 128:
2.4 Canonical quantization 47 Criti
- Page 132:
2.5 Light-cone gauge quantization 4
- Page 136:
2.5 Light-cone gauge quantization 5
- Page 140:
Homework Problems 53 The closed str
- Page 144:
(i) Dirichlet boundary conditions a
- Page 148:
Homework Problems 57 PROBLEM 2.11 T
- Page 152:
3.1 Conformal field theory 59 and r
- Page 156:
3.1 Conformal field theory 61 rotat
- Page 160:
symmetry, this tensor is also conse
- Page 164:
3.1 Conformal field theory 65 This
- Page 168:
3.1 Conformal field theory 67 Such
- Page 172:
or the equivalent commutation relat
- Page 176:
3.1 Conformal field theory 71 An im
- Page 180:
3.1 Conformal field theory 73 is pr
- Page 184:
SOLUTION 3.2 BRST quantization 75 A
- Page 188:
where TX is given in Eq. (3.23) and
- Page 192:
3.2 BRST quantization 79 in differe
- Page 196:
SOLUTION 3.3 Background fields 81 U
- Page 200:
3.3 Background fields 83 unoriented
- Page 204:
3.4 Vertex operators 85 3.4 Vertex
- Page 208:
3.4 Vertex operators 87 must act on
- Page 212:
3.5 The structure of string perturb
- Page 216:
3.5 The structure of string perturb
- Page 220:
3.5 The structure of string perturb
- Page 224:
3.5 The structure of string perturb
- Page 228:
SOLUTION 3.5 The structure of strin
- Page 232:
3.6 The linear-dilaton vacuum and n
- Page 236:
3.7 Witten’s open-string field th
- Page 240:
3.7 Witten’s open-string field th
- Page 244:
3.7 Witten’s open-string field th
- Page 248:
form Homework Problems 107 Φ(z) =
- Page 252:
4 Strings with world-sheet supersym
- Page 256:
4.1 Ramond-Neveu-Schwarz strings 11
- Page 260:
4.2 Global world-sheet supersymmetr
- Page 264:
4.2 Global world-sheet supersymmetr
- Page 268:
4.2 Global world-sheet supersymmetr
- Page 272:
4.3 Constraint equations and confor
- Page 276:
EXERCISES 4.3 Constraint equations
- Page 280:
4.4 Boundary conditions and mode ex
- Page 284:
4.5 Canonical quantization of the R
- Page 288:
4.5 Canonical quantization of the R
- Page 292:
4.5 Canonical quantization of the R
- Page 296:
4.6 Light-cone gauge quantization o
- Page 300:
4.6 Light-cone gauge quantization o
- Page 304:
4.6 Light-cone gauge quantization o
- Page 308:
are given by 4.6 Light-cone gauge q
- Page 312:
4.6 Light-cone gauge quantization o
- Page 316:
4.7 SCFT and BRST 141 which now has
- Page 320:
4.7 SCFT and BRST 143 These contrib
- Page 324:
Homework Problems 145 needs to incl
- Page 328:
Homework Problems 147 PROBLEM 4.14
- Page 332:
5.1 The D0-brane action 149 5.1 The
- Page 336:
5.1 The D0-brane action 151 It turn
- Page 340:
Thus δ(S1 + S2) = −2m 5.1 The D
- Page 344:
SOLUTION 5.2 The supersymmetric str
- Page 348:
5.2 The supersymmetric string actio
- Page 352:
5.2 The supersymmetric string actio
- Page 356:
5.3 Quantization of the GS action 1
- Page 360:
5.3 Quantization of the GS action 1
- Page 364:
5.3 Quantization of the GS action 1
- Page 368:
5.3 Quantization of the GS action 1
- Page 372:
5.4 Gauge anomalies and their cance
- Page 376:
5.4 Gauge anomalies and their cance
- Page 380:
5.4 Gauge anomalies and their cance
- Page 384:
5.4 Gauge anomalies and their cance
- Page 388:
5.4 Gauge anomalies and their cance
- Page 392:
and ω3 = (ω3L − ω3Y)/4, where
- Page 396:
5.4 Gauge anomalies and their cance
- Page 400:
5.4 Gauge anomalies and their cance
- Page 404:
Homework Problems 185 PROBLEM 5.2 I
- Page 408:
6 T-duality and D-branes String the
- Page 412:
6.1 The bosonic string and Dp-brane
- Page 416:
6.1 The bosonic string and Dp-brane
- Page 420:
6.1 The bosonic string and Dp-brane
- Page 424:
6.1 The bosonic string and Dp-brane
- Page 428:
6.1 The bosonic string and Dp-brane
- Page 432:
6.1 The bosonic string and Dp-brane
- Page 436:
6.1 The bosonic string and Dp-brane
- Page 440:
6.2 D-branes in type II superstring
- Page 444:
6.2 D-branes in type II superstring
- Page 448:
6.2 D-branes in type II superstring
- Page 452:
6.2 D-branes in type II superstring
- Page 456:
6.2 D-branes in type II superstring
- Page 460:
6.2 D-branes in type II superstring
- Page 464:
6.2 D-branes in type II superstring
- Page 468:
6.2 D-branes in type II superstring
- Page 472:
6.2 D-branes in type II superstring
- Page 476:
associated with the Fock-space stat
- Page 480:
6.3 Type I superstring theory 223 O
- Page 484:
6.3 Type I superstring theory 225 T
- Page 488:
6.4 T-duality in the presence of ba
- Page 492:
6.5 World-volume actions for D-bran
- Page 496:
6.5 World-volume actions for D-bran
- Page 500:
6.5 World-volume actions for D-bran
- Page 504:
6.5 World-volume actions for D-bran
- Page 508:
6.5 World-volume actions for D-bran
- Page 512:
6.5 World-volume actions for D-bran
- Page 516:
6.5 World-volume actions for D-bran
- Page 520:
SOLUTION Because 6.5 World-volume a
- Page 524:
Homework Problems 245 theory for ra
- Page 528:
PROBLEM 6.11 Homework Problems 247
- Page 532:
7 The heterotic string The precedin
- Page 536:
7.1 Nonabelian gauge symmetry in st
- Page 540:
7.2 Fermionic construction of the h
- Page 544:
7.2 Fermionic construction of the h
- Page 548:
7.2 Fermionic construction of the h
- Page 552:
7.2 Fermionic construction of the h
- Page 556:
7.2 Fermionic construction of the h
- Page 560:
where 7.2 Fermionic construction of
- Page 564:
7.3 Toroidal compactification 265 E
- Page 568:
7.3 Toroidal compactification 267 T
- Page 572:
where 4 or the inverse 7.3 Toroidal
- Page 576:
7.3 Toroidal compactification 271 t
- Page 580:
7.3 Toroidal compactification 273 N
- Page 584:
7.3 Toroidal compactification 275 w
- Page 588:
7.3 Toroidal compactification 277 I
- Page 592:
• Using Eq. (7.66), one obtains 7
- Page 596:
7.3 Toroidal compactification 281 N
- Page 600:
7.3 Toroidal compactification 283 E
- Page 604:
7.3 Toroidal compactification 285 F
- Page 608:
7.4 Bosonic construction of the het
- Page 612:
7.4 Bosonic construction of the het
- Page 616:
Homework Problems 291 To derive thi
- Page 620:
Homework Problems 293 in each case?
- Page 624:
Homework Problems 295 where the coo
- Page 628:
M-theory and string duality 297 tha
- Page 632:
M-theory and string duality 299 exp
- Page 636:
8.1 Low-energy effective actions 30
- Page 640:
8.1 Low-energy effective actions 30
- Page 644:
8.1 Low-energy effective actions 30
- Page 648:
8.1 Low-energy effective actions 30
- Page 652:
In terms of the elfbein E A M 8.1 L
- Page 656:
8.1 Low-energy effective actions 31
- Page 660:
8.1 Low-energy effective actions 31
- Page 664:
8.1 Low-energy effective actions 31
- Page 668:
8.1 Low-energy effective actions 31
- Page 672:
8.1 Low-energy effective actions 31
- Page 676:
8.1 Low-energy effective actions 32
- Page 680:
8.2 S-duality 323 with the correspo
- Page 684:
8.2 S-duality 325 This leads to the
- Page 688:
8.2 S-duality 327 Type IIB S-dualit
- Page 692:
8.3 M-theory 329 since an SL(2, ) t
- Page 696:
8.3 M-theory 331 states, and carry
- Page 700:
8.3 M-theory 333 answering this que
- Page 704: spectrum, while the zero mode of 8.
- Page 708: 8.3 M-theory 337 the weakly coupled
- Page 712: 8.4 M-theory dualities 339 An M-the
- Page 716: 8.4 M-theory dualities 341 the type
- Page 720: 8.4 M-theory dualities 343 which co
- Page 724: that 8.4 M-theory dualities 345 T (
- Page 728: 8.4 M-theory dualities 347 d5 = dim
- Page 732: SOLUTION 8.4 M-theory dualities 349
- Page 736: Homework Problems 351 M2-brane wrap
- Page 740: Homework Problems 353 (i) Use the r
- Page 744: String geometry 355 is typically gi
- Page 748: String geometry 357 erotic string r
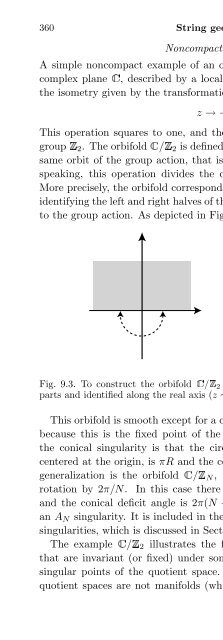
- Page 752: 9.1 Orbifolds 359 four-dimensional
- Page 758: 362 String geometry In the quantum
- Page 762: 364 String geometry of the manifold
- Page 766: 366 String geometry 9.3 Examples of
- Page 770: 368 String geometry Hodge numbers o
- Page 774: 370 String geometry is a compact K
- Page 778: 372 String geometry proportional to
- Page 782: 374 String geometry This leads to t
- Page 786: 376 String geometry independent cho
- Page 790: 378 String geometry This implies th
- Page 794: 380 String geometry Kähler form an
- Page 798: 382 String geometry satisfies √ g
- Page 802: 384 String geometry In writing this
- Page 806:
386 String geometry This section an
- Page 810:
388 String geometry torus is descri
- Page 814:
390 String geometry where Mr is any
- Page 818:
392 String geometry Writing the met
- Page 822:
394 String geometry Since the prepo
- Page 826:
396 String geometry A change in the
- Page 830:
398 String geometry For these choic
- Page 834:
400 String geometry coefficients. W
- Page 838:
402 String geometry four fermionic
- Page 842:
404 String geometry a vanishing cyc
- Page 846:
406 String geometry global supersym
- Page 850:
408 String geometry similar fashion
- Page 854:
410 String geometry where K = 1 2 (
- Page 858:
412 String geometry versa. An early
- Page 862:
414 String geometry by complex-stru
- Page 866:
416 String geometry holonomy group,
- Page 870:
418 String geometry rather than SU(
- Page 874:
420 String geometry to the case of
- Page 878:
422 String geometry For example, in
- Page 882:
424 String geometry example is the
- Page 886:
426 String geometry type IIA string
- Page 890:
428 String geometry which transform
- Page 894:
430 String geometry The tension of
- Page 898:
432 String geometry fibration. Only
- Page 902:
434 String geometry folds, constrai
- Page 906:
436 String geometry to that in Exer
- Page 910:
438 String geometry be interpreted
- Page 914:
440 String geometry SOLUTION An inf
- Page 918:
442 String geometry to a zero form
- Page 922:
444 String geometry Riemannian geom
- Page 926:
446 String geometry map tensors to
- Page 930:
448 String geometry a possible holo
- Page 934:
450 String geometry as the complex
- Page 938:
452 String geometry . ✷ EXERCISE
- Page 942:
454 String geometry PROBLEM 9.8 Use
- Page 946:
10 Flux compactifications Moduli-sp
- Page 950:
458 Flux compactifications This hap
- Page 954:
460 Flux compactifications the stan
- Page 958:
462 Flux compactifications coordina
- Page 962:
464 Flux compactifications Fig. 10.
- Page 966:
466 Flux compactifications The last
- Page 970:
468 Flux compactifications forms (a
- Page 974:
470 Flux compactifications G µν G
- Page 978:
472 Flux compactifications Fig. 10.
- Page 982:
474 Flux compactifications Superpot
- Page 986:
476 Flux compactifications where dz
- Page 990:
478 Flux compactifications Since m
- Page 994:
480 Flux compactifications 10.2 Flu
- Page 998:
482 Flux compactifications is the e
- Page 1002:
484 Flux compactifications the fibe
- Page 1006:
486 Flux compactifications The tota
- Page 1010:
488 Flux compactifications S 3 S 2
- Page 1014:
490 Flux compactifications be true
- Page 1018:
492 Flux compactifications where gs
- Page 1022:
494 Flux compactifications Fig. 10.
- Page 1026:
496 Flux compactifications Negative
- Page 1030:
498 Flux compactifications will be
- Page 1034:
500 Flux compactifications As you a
- Page 1038:
502 Flux compactifications where K
- Page 1042:
504 Flux compactifications is of in
- Page 1046:
506 Flux compactifications V(σ) Fi
- Page 1050:
508 Flux compactifications where Da
- Page 1054:
510 Flux compactifications Fig. 10.
- Page 1058:
512 Flux compactifications M, N, P
- Page 1062:
514 Flux compactifications By defin
- Page 1066:
516 Flux compactifications In this
- Page 1070:
518 Flux compactifications As a res
- Page 1074:
520 Flux compactifications constant
- Page 1078:
522 Flux compactifications a way th
- Page 1082:
524 Flux compactifications F3 −
- Page 1086:
526 Flux compactifications One fina
- Page 1090:
528 Flux compactifications Friedman
- Page 1094:
530 Flux compactifications If there
- Page 1098:
532 Flux compactifications cosmolog
- Page 1102:
534 Flux compactifications to Eq. (
- Page 1106:
536 Flux compactifications but not
- Page 1110:
538 Flux compactifications e-foldin
- Page 1114:
540 Flux compactifications of makin
- Page 1118:
542 Flux compactifications Here W0
- Page 1122:
544 Flux compactifications [γmn,
- Page 1126:
546 Flux compactifications complex
- Page 1130:
548 Flux compactifications Eq. (10.
- Page 1134:
550 Black holes in string theory th
- Page 1138:
552 Black holes in string theory di
- Page 1142:
554 Black holes in string theory He
- Page 1146:
556 Black holes in string theory r=
- Page 1150:
558 Black holes in string theory
- Page 1154:
560 Black holes in string theory of
- Page 1158:
562 Black holes in string theory Th
- Page 1162:
564 Black holes in string theory wh
- Page 1166:
566 Black holes in string theory SO
- Page 1170:
568 Black holes in string theory Th
- Page 1174:
570 Black holes in string theory st
- Page 1178:
572 Black holes in string theory M-
- Page 1182:
574 Black holes in string theory ro
- Page 1186:
576 Black holes in string theory In
- Page 1190:
578 Black holes in string theory Fi
- Page 1194:
580 Black holes in string theory (2
- Page 1198:
582 Black holes in string theory SO
- Page 1202:
584 Black holes in string theory ju
- Page 1206:
586 Black holes in string theory No
- Page 1210:
588 Black holes in string theory co
- Page 1214:
590 Black holes in string theory ba
- Page 1218:
592 Black holes in string theory Th
- Page 1222:
594 Black holes in string theory Fi
- Page 1226:
596 Black holes in string theory su
- Page 1230:
598 Black holes in string theory wh
- Page 1234:
600 Black holes in string theory 28
- Page 1238:
602 Black holes in string theory is
- Page 1242:
604 Black holes in string theory wh
- Page 1246:
606 Black holes in string theory S-
- Page 1250:
608 Black holes in string theory PR
- Page 1254:
12 Gauge theory/string theory duali
- Page 1258:
612 Gauge theory/string theory dual
- Page 1262:
614 Gauge theory/string theory dual
- Page 1266:
616 Gauge theory/string theory dual
- Page 1270:
618 Gauge theory/string theory dual
- Page 1274:
620 Gauge theory/string theory dual
- Page 1278:
622 Gauge theory/string theory dual
- Page 1282:
624 Gauge theory/string theory dual
- Page 1286:
626 Gauge theory/string theory dual
- Page 1290:
628 Gauge theory/string theory dual
- Page 1294:
630 Gauge theory/string theory dual
- Page 1298:
632 Gauge theory/string theory dual
- Page 1302:
634 Gauge theory/string theory dual
- Page 1306:
636 Gauge theory/string theory dual
- Page 1310:
638 Gauge theory/string theory dual
- Page 1314:
640 Gauge theory/string theory dual
- Page 1318:
642 Gauge theory/string theory dual
- Page 1322:
644 Gauge theory/string theory dual
- Page 1326:
646 Gauge theory/string theory dual
- Page 1330:
648 Gauge theory/string theory dual
- Page 1334:
650 Gauge theory/string theory dual
- Page 1338:
652 Gauge theory/string theory dual
- Page 1342:
654 Gauge theory/string theory dual
- Page 1346:
656 Gauge theory/string theory dual
- Page 1350:
658 Gauge theory/string theory dual
- Page 1354:
660 Gauge theory/string theory dual
- Page 1358:
662 Gauge theory/string theory dual
- Page 1362:
664 Gauge theory/string theory dual
- Page 1366:
666 Gauge theory/string theory dual
- Page 1370:
668 Gauge theory/string theory dual
- Page 1374:
670 Gauge theory/string theory dual
- Page 1378:
672 Gauge theory/string theory dual
- Page 1382:
674 Gauge theory/string theory dual
- Page 1386:
676 Gauge theory/string theory dual
- Page 1390:
678 Gauge theory/string theory dual
- Page 1394:
680 Gauge theory/string theory dual
- Page 1398:
682 Gauge theory/string theory dual
- Page 1402:
684 Gauge theory/string theory dual
- Page 1406:
686 Gauge theory/string theory dual
- Page 1410:
688 Gauge theory/string theory dual
- Page 1414:
Bibliographic discussion In the fol
- Page 1418:
692 Bibliographic discussion The BR
- Page 1422:
694 Bibliographic discussion derive
- Page 1426:
696 Bibliographic discussion which
- Page 1430:
698 Bibliographic discussion Maldac
- Page 1434:
Bibliography Abouelsaood, A., Calla
- Page 1438:
702 Bibliography Singapore: World S
- Page 1442:
704 Bibliography Brink, L., and Nie
- Page 1446:
706 Bibliography E-print hep-th/000
- Page 1450:
708 Bibliography hep-th/0105203. Eg
- Page 1454:
710 Bibliography Phys., 71, 983-108
- Page 1458:
712 Bibliography hep-th/9802109. Gu
- Page 1462:
714 Bibliography Johnson, C. V. (20
- Page 1466:
716 Bibliography Lerche, W., Schell
- Page 1470:
718 Bibliography Montonen, C. (1974
- Page 1474:
720 Bibliography Polchinski, J., an
- Page 1478:
722 Bibliography Sen, A. (1999). No
- Page 1482:
724 Bibliography Tseytlin, A. A. (1
- Page 1486:
acceleration equation, 528 action p
- Page 1490:
728 Index Calabi-Yau four-fold, 458
- Page 1494:
730 Index with E6,6 symmetry, 570 c
- Page 1498:
732 Index Friedmann equation, 528 F
- Page 1502:
734 Index dual Coxeter number, 69 e
- Page 1506:
736 Index homogeneity equation, 603
- Page 1510:
738 Index superconformal symmetry,