tkz-euclid e 1.16 c AlterMundus

More documents

Recommendations

Info

$The 'pst-ob3d' package A PSTricks package for three ... - BaKoMa TeX$

$The cjw-latex Macro Collection$

$Printing Z and Object-Z LATEX documents 1 Introduction 2 Schema ...$

$lineno.sty v4.41 2005/11/02 A LATEX package to attach line ...$

$Arev Sans for TeX and LaTeX$

14 Polygones 84 SECTION 14 Polygones 14.1 Définition des triangles Les macros suivantes vont permettre de définir ou de construire un triangle à partir au moins de deux points. Pour le moment, il est possible de définir les triangles suivants : – two angles détermine un triangle connaissant deux angles, – equilateral détermine un triangle équilatéral, – half détermine un triangle rectangle tel que le rapport des mesures des deux côtés adjacents à l’angle droit soit égal à 2, – pythagore détermine un triangle rectangle dont les mesures des côtés sont proportionnelles à 3, 4 et 5, – school détermine un triangle rectangle dont les angles sont 30, 60 et 90 degrés, – golden détermine un triangle rectangle tel que le rapport des mesures des deux côtés adjacents à l’angle droit soit égal Φ = 1,618034, J’ai choisi comme dénomination « triangle doré » car il rpovient du rectangle d’or et j’ai conservé la dénomination « triangle d’or » ou encore « triangle d’Euclide » pour le triangle isocèle dont les angles à la base sont de 72 degrés, – gold ou euclide pour le triangle d’or, – cheops détermine un troisième point tel que le triangle soit isocèle dont les mesures des côtés sont proportionnelles à 2, Φ et Φ. \tkzDefTriangle[〈local options〉](〈A,B〉) les points sont ordonnés car le triangle est construit en suivant le sens direct du cercle trigonométrique. Cette macro est soit utilisée en partenariat avec \tkzGetPoint soit en utilisant tkzPointResult s’il n’est pas nécessaire de conserver le nom. options défaut définition two angles= #1 and #2 no defaut triangle connaissant deux angles equilateral no defaut triangle équilatéral pythagore no defaut proportionnel au triangle de pythagore 3-4-5 school no defaut angles de 30, 60 et 90 degrés gold no defaut angles de 72, 72 et 36 degrés, A est le sommet euclide no defaut identique au précédent mais [AB] est la base golden no defaut rectangle en B et AB/AC = Φ cheops no defaut AC=BC, AC et BC sont proportionnels à 2 et Φ. 14.1.1 triangle doré (golden) A C B \begin{tikzpicture}[scale=.8] \tkzInit[xmax=5,ymax=3] \tkzClip[space=.5] \tkzDefPoint(0,0){A} \tkzDefPoint(4,0){B} \tkzDefTriangle[golden](A,B)\tkzGetPoint{C} \tkzDrawPolygon(A,B,C) \tkzDrawPoints(A,B,C) \tkzLabelPoints(A,B) \tkzDrawBisector(A,C,B) \tkzLabelPoints[above](C) \end{tikzpicture} tkz-euclide AlterMundus
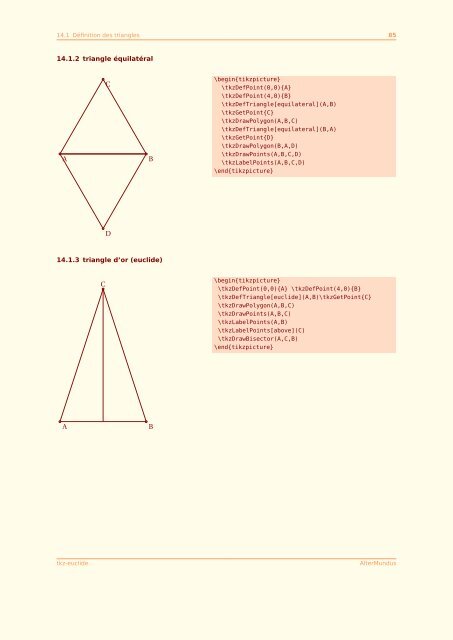
14.1 Définition des triangles 85 14.1.2 triangle équilatéral A C B \begin{tikzpicture} \tkzDefPoint(0,0){A} \tkzDefPoint(4,0){B} \tkzDefTriangle[equilateral](A,B) \tkzGetPoint{C} \tkzDrawPolygon(A,B,C) \tkzDefTriangle[equilateral](B,A) \tkzGetPoint{D} \tkzDrawPolygon(B,A,D) \tkzDrawPoints(A,B,C,D) \tkzLabelPoints(A,B,C,D) \end{tikzpicture} D 14.1.3 triangle d’or (euclide) C \begin{tikzpicture} \tkzDefPoint(0,0){A} \tkzDefPoint(4,0){B} \tkzDefTriangle[euclide](A,B)\tkzGetPoint{C} \tkzDrawPolygon(A,B,C) \tkzDrawPoints(A,B,C) \tkzLabelPoints(A,B) \tkzLabelPoints[above](C) \tkzDrawBisector(A,C,B) \end{tikzpicture} A B tkz-euclide AlterMundus
Page 1 and 2:
tkz-euclide 1.16 c AlterMundus Alte
Page 3 and 4:
Table des matières 3 Table des mat
Page 5 and 6:
Table des matières 5 10.3.3 Constr
Page 7 and 8:
Table des matières 7 16 Utilisatio
Page 9 and 10:
1 Installation 9 SECTION 1 Installa
Page 11 and 12:
1.3 Chargement des fichiers avec us
Page 13 and 14:
3 Syntaxe 13 SECTION 3 Syntaxe Quel
Page 15 and 16:
4 Exemple minimal, mais complet 15
Page 17 and 18:
5 Résumé de tkz-base 17 SECTION 5
Page 19 and 20:
5.6 \tkzGrid et les couleurs 19 y 3
Page 21 and 22:
6.1 Définition d’un point en coo
Page 23 and 24:
6.3 Point relativement à un autre
Page 25 and 26:
6.5 Tracer des points \tkzDrawPoint
Page 27 and 28:
6.6 Ajouter des labels aux points \
Page 29 and 30:
7 Points particuliers 29 SECTION 7
Page 31 and 32:
7.3 \tkzCentroid 31 7.3 \tkzCentroi
Page 33 and 34: 8 Définition aléatoire de points
Page 35 and 36: 8.5 Milieu d’un segment au compas
Page 37 and 38: 9.1 La réflexion ou symétrie orth
Page 39 and 40: 9.3 La projection 39 9.3 La project
Page 41 and 42: 9.5 La rotation 41 9.5 La rotation
Page 43 and 44: 9.7 L’inversion par rapport à un
Page 45 and 46: 9.8 Exemple de translation 45 Il ex
Page 47 and 48: 9.10 Flower of Life 47 9.10 Flower
Page 49 and 50: 9.12 Constructions de certaines tra
Page 51 and 52: 9.12 Constructions de certaines tra
Page 53 and 54: 10.2 Intersection d’une droite et
Page 61 and 62: 10.3 Intersection de deux cercles 6
Page 67 and 68: 11.2 Tracer une droite 67 11.1.2 Ex
Page 69 and 70: 11.2 Tracer une droite 69 Il est po
Page 71 and 72: 11.2 Tracer une droite 71 11.2.4 Un
Page 73 and 74: 11.5 Montrer les constructions de c
Page 75 and 76: 12 Les segments 75 SECTION 12 Les s
Page 77 and 78: 12.4 Marquer des segments \tkzMarkS
Page 79 and 80: 12.5 Exemple de rotation 79 \tkzLab
Page 81 and 82: 13 Définition de points à l’aid
Page 83: 13.1 \tkzDefPointWith 83 C A B \beg
Page 87 and 88: 14.3 Les médianes 87 14.3 Les méd
Page 89 and 90: 14.7 Définir les points d’un car
Page 91 and 92: 14.8 Tracé un carré 91 14.8 Trac
Page 93 and 94: 14.11 Clipper un polygone 93 \begin
Page 95 and 96: 14.12 Colorier un polygone 95 14.12
Page 97 and 98: 15.1 Caractéristiques d’un cercl
Page 103 and 104: 15.2 Tracer un cercle 103 15.2 Trac
Page 105 and 106: 15.2 Tracer un cercle 105 15.2.3 Ca
Page 107 and 108: 15.3 Colorier un disque 107 15.3 Co
Page 109 and 110: 15.4 Clipper un disque 109 15.4.3 E
Page 111 and 112: 15.6 Tangente à un cercle 111 15.6
Page 113 and 114: 16 Utilisation du compas 113 SECTIO
Page 115 and 116: 16.3 Macro de configuration \tkzSet
Page 117 and 118: 17.2 \tkzDrawSector et rotate 117 1
Page 119 and 120: 17.6 \tkzFillSector et rotate 119 \
Page 121 and 122: 18.2 \tkzDrawArc et towards 121 18.
Page 123 and 124: 180 190 270 280 19 Rapporteurs 123
Page 125 and 126: 19.3 Le rapporteur original semi-ci
Page 127 and 128: 19.5 Le rapporteur semi-circulaire
Page 129 and 130: 20 Quelques outils 129 SECTION 20 Q
Page 131 and 132: 20.3 Angle formé par une droite av
Page 133 and 134: 20.6 Angle formé par trois points
Page 135 and 136:
20.9 Transformation de pt en cm ou
Page 137 and 138:
21.3 \tkzSetUpCompass 137 21.3 \tkz
Page 139 and 140:
22.1 Triangles isocèles semblables
Page 141 and 142:
22.2 Hauteurs d’un triangle 141 2
Page 143 and 144:
23 Gallery : Some examples 143 SECT
Page 145 and 146:
23.3 How to construct the tangent l
Page 147 and 148:
23.5 About right triangle 147 23.5
Page 149 and 150:
23.7 Example from Dimitris Kapeta 1
Page 151 and 152:
23.9 Example 2 from John Kitzmiller
Page 153 and 154:
23.11 Example 4 from John Kitzmille
Page 155 and 156:
24.1 Erreurs les plus fréquentes 1
Page 157 and 158:
Index 157 \tkzActivOff . . . . . .
Page 159 and 160:
Index 159 rotation . . . . . . . .
Page 161 and 162:
Index 161 \tkzDrawLines[〈local op
Page 163 and 164:
Index 163 \tkzGetPoint(A) . . . . .
Page 165 and 166:
Index 165 \tkzpttocm . . . . . . .
show all

tkz-euclid e 1.16 c AlterMundus

Create successful ePaper yourself

Delete template?

Save as template?