Computermethoden zur Lösung einiger konkreter kombinatorischer ...

22 2 Ramsey-Zahlen
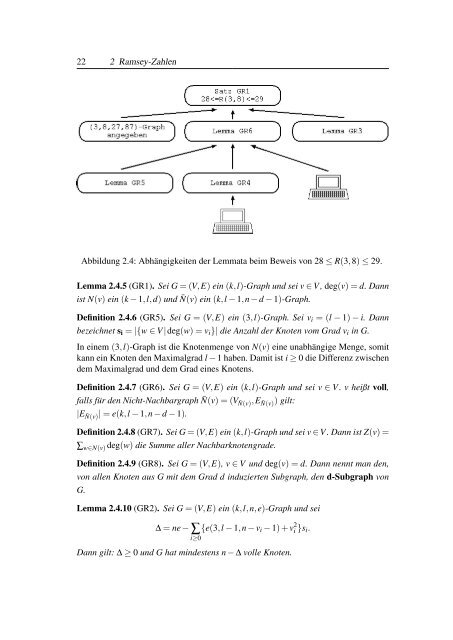
Abbildung 2.4: Abhängigkeiten der Lemmata beim Beweis von 28 ≤ R(3,8) ≤ 29.
Lemma 2.4.5 (GR1). Sei G = (V,E) ein (k,l)-Graph und sei v ∈ V , deg(v) = d. Dann
ist N(v) ein (k − 1,l,d) und ¯N(v) ein (k,l − 1,n − d − 1)-Graph.
Definition 2.4.6 (GR5). Sei G = (V,E) ein (3,l)-Graph. Sei vi = (l − 1) − i. Dann
bezeichnet si = |{w ∈ V |deg(w) = vi}| die Anzahl der Knoten vom Grad vi in G.
In einem (3,l)-Graph ist die Knotenmenge von N(v) eine unabhängige Menge, somit
kann ein Knoten den Maximalgrad l −1 haben. Damit ist i ≥ 0 die Differenz zwischen
dem Maximalgrad und dem Grad eines Knotens.
Definition 2.4.7 (GR6). Sei G = (V,E) ein (k,l)-Graph und sei v ∈ V . v heißt voll,
falls für den Nicht-Nachbargraph ¯N(v) = (V ¯N(v),E ¯N(v)) gilt:
|E ¯N(v)| = e(k,l − 1,n − d − 1).
Definition 2.4.8 (GR7). Sei G = (V,E) ein (k,l)-Graph und sei v ∈ V . Dann ist Z(v) =
∑w∈N(v) deg(w) die Summe aller Nachbarknotengrade.
Definition 2.4.9 (GR8). Sei G = (V,E), v ∈ V und deg(v) = d. Dann nennt man den,
von allen Knoten aus G mit dem Grad d induzierten Subgraph, den d-Subgraph von
G.
Lemma 2.4.10 (GR2). Sei G = (V,E) ein (k,l,n,e)-Graph und sei
∆ = ne − ∑{e(3,l − 1,n − vi − 1) + v
i≥0
2 i }si.
Dann gilt: ∆ ≥ 0 und G hat mindestens n − ∆ volle Knoten.