PDF 1.938kB

4.4. QUALITY OF TRANSFORMATIONS 31
applying the following equation where ∇F is the Jacobian matrix of F .
Σ xy = ∇F dα Σ dα ∇Fdα
T ⎡ ⎤ ⎡
δf 1 δf 1
with ∇F dα = ⎣ δd δα ⎦ = ⎣ cos α
δf 2 δf 2
δd δα
sin α
⎡ ⎤
Σ dα = ⎣ σ2 d
0
⎦
0 σα
2
⎤
−d sin α
⎦
d cos α
The new matrix Σ xy is only an approximation, because with ∇F the derivation at point [ ] T
µ x µ y is
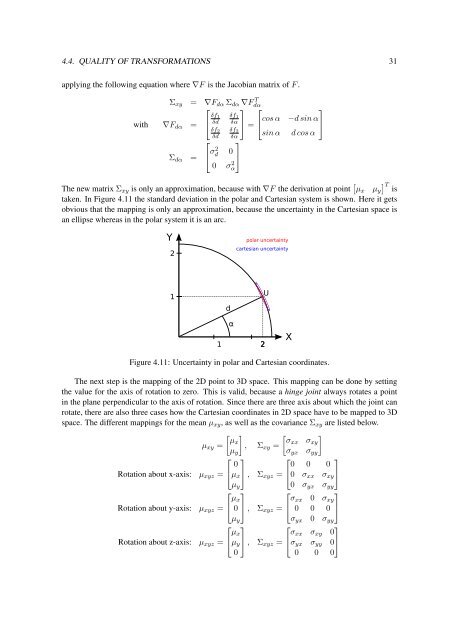
taken. In Figure 4.11 the standard deviation in the polar and Cartesian system is shown. Here it gets
obvious that the mapping is only an approximation, because the uncertainty in the Cartesian space is
an ellipse whereas in the polar system it is an arc.
Y
2
polar uncertainty
cartesian uncertainty
1
d
U
α
1 2
X
Figure 4.11: Uncertainty in polar and Cartesian coordinates.
The next step is the mapping of the 2D point to 3D space. This mapping can be done by setting
the value for the axis of rotation to zero. This is valid, because a hinge joint always rotates a point
in the plane perpendicular to the axis of rotation. Since there are three axis about which the joint can
rotate, there are also three cases how the Cartesian coordinates in 2D space have to be mapped to 3D
space. The different mappings for the mean µ xy , as well as the covariance Σ xy are listed below.
[ ] [ ]
µx
σxx σ
µ xy = , Σ
µ xy =
xy
y σ yx σ yy
⎡ ⎤ ⎡
⎤
0
0 0 0
Rotation about x-axis: µ xyz = ⎣µ x
⎦ , Σ xyz = ⎣0 σ xx σ xy
⎦
µ y 0 σ yx σ yy
⎡ ⎤ ⎡
⎤
µ x
σ xx 0 σ xy
Rotation about y-axis: µ xyz = ⎣ 0 ⎦ , Σ xyz = ⎣ 0 0 0 ⎦
µ y σ yx 0 σ yy
⎡ ⎤ ⎡
⎤
µ x
σ xx σ xy 0
Rotation about z-axis: µ xyz = ⎣µ y
⎦ , Σ xyz = ⎣σ yx σ yy 0⎦
0
0 0 0