Modelling Dependence with Copulas - IFOR

2.4 Copulas and Random Variables
M
W
Y1
0.0 0.2 0.4 0.6 0.8 1.0
••
••
••
••
•
•
•
•
•
••
••
••
•
•
•
•
•
•
•
•
••
• •
•
•
•
•
•
•
••
•
•
•
•
•
•
•
•
•
•
••
••
•
•
••
•
•
•
•
•
•
Y2
0.0 0.2 0.4 0.6 0.8 1.0
•
••
•
•
•
•
•
•
••
•
•
•
•
•
•
••
•
•
•
•
•• •
•
•
••
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
••
•
•
•
••
•
•
•
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.2 0.4 0.6 0.8 1.0
X1
X2
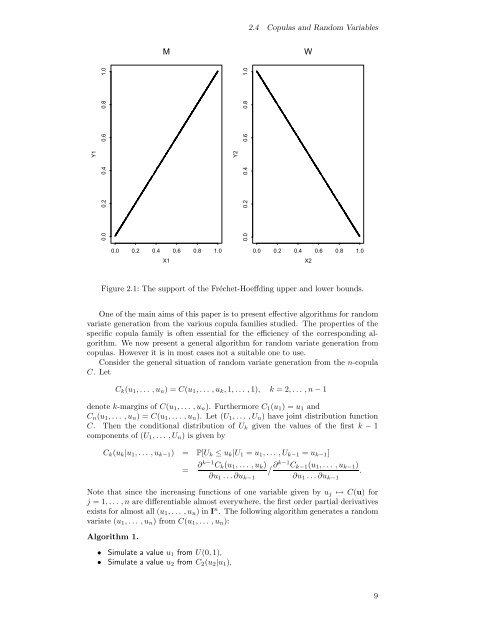
Figure 2.1: The support of the Fréchet-Hoeffding upper and lower bounds.
One of the main aims of this paper is to present effective algorithms for random
variate generation from the various copula families studied. The properties of the
specific copula family is often essential for the efficiency of the corresponding algorithm.
We now present a general algorithm for random variate generation from
copulas. However it is in most cases not a suitable one to use.
Consider the general situation of random variate generation from the n-copula
C. Let
C k (u 1 ,... ,u n )=C(u 1 ,... ,u k , 1,... ,1), k =2,... ,n− 1
denote k-margins of C(u 1 ,... ,u n ). Furthermore C 1 (u 1 )=u 1 and
C n (u 1 ,... ,u n )=C(u 1 ,... ,u n ). Let (U 1 ,... ,U n ) have joint distribution function
C. Then the conditional distribution of U k given the values of the first k − 1
components of (U 1 ,... ,U n )isgivenby
C k (u k |u 1 ,... ,u k−1 ) = P[U k ≤ u k |U 1 = u 1 ,... ,U k−1 = u k−1 ]
= ∂k−1 C k (u 1 ,... ,u k ) /∂ k−1 C k−1 (u 1 ,... ,u k−1 )
.
∂u 1 ...∂u k−1 ∂u 1 ...∂u k−1
Note that since the increasing functions of one variable given by u j ↦→ C(u) for
j =1,... ,n are differentiable almost everywhere, the first order partial derivatives
exists for almost all (u 1 ,... ,u n )inI n . The following algorithm generates a random
variate (u 1 ,... ,u n ) from C(u 1 ,... ,u n ):
Algorithm 1.
• Simulate a value u 1 from U(0, 1),
• Simulate a value u 2 from C 2 (u 2 |u 1 ),
9