Cap. 4 Complejidad temporal de algoritmos - Inicio

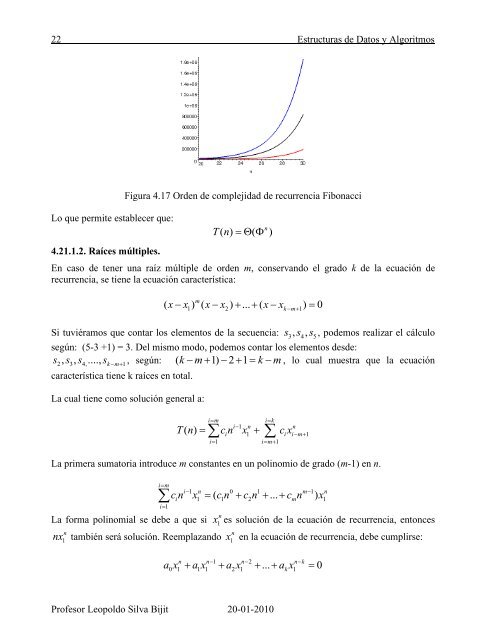
22 Estructuras de Datos y AlgoritmosLo que permite establecer que:4.21.1.2. Raíces múltiples.Figura 4.17 Orden de complejidad de recurrencia FibonaccinTn ( ) ( )En caso de tener una raíz múltiple de orden m, conservando el grado k de la ecuación derecurrencia, se tiene la ecuación característica:m( x x1 ) ( x x2) ... ( x xk m 1) 0Si tuviéramos que contar los elementos de la secuencia: s3, s4,s5, podemos realizar el cálculosegún: (5-3 +1) = 3. Del mismo modo, podemos contar los elementos desde:s2, s3, s4, ...., sk m 1, según: ( k m 1) 2 1 k m , lo cual muestra que la ecuacióncaracterística tiene k raíces en total.La cual tiene como solución general a:imiki1n n i 1 i im1i1 im1T( n) c n x c xLa primera sumatoria introduce m constantes en un polinomio de grado (m-1) en n.imi1c n x ( c n c n ... c n ) xii1 n 0 1 m1n1 1 2 m 1nLa forma polinomial se debe a que si x1es solución de la ecuación de recurrencia, entoncesnnnx1también será solución. Reemplazando1x en la ecuación de recurrencia, debe cumplirse:a x a x a x ... a x 0n n1 n2nk0 1 1 1 2 1 k 1Profesor Leopoldo Silva Bijit 20-01-2010