Cap. 4 Complejidad temporal de algoritmos - Inicio

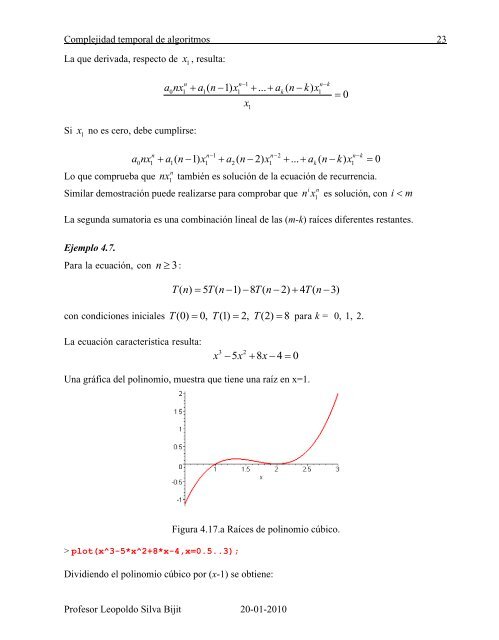
Complejidad temporal de algoritmos 23La que derivada, respecto de x1, resulta:a nx a ( n 1) x ... a ( n k)xxn n1nk0 1 1 1 k11 0Si x1no es cero, debe cumplirse:a nx a ( n 1) x a ( n 2) x ... a ( n k) x 0n n1 n2nk0 1 1 1 2 1 k1nLo que comprueba que nx1también es solución de la ecuación de recurrencia.i nSimilar demostración puede realizarse para comprobar que nx1es solución, con i mLa segunda sumatoria es una combinación lineal de las (m-k) raíces diferentes restantes.Ejemplo 4.7.Para la ecuación, con n 3:T( n) 5 T( n 1) 8 T( n 2) 4 T( n 3)con condiciones iniciales T(0) 0, T(1) 2, T(2) 8 para k = 0, 1, 2.La ecuación característica resulta:3 2x x x5 8 4 0Una gráfica del polinomio, muestra que tiene una raíz en x=1.> plot(x^3-5*x^2+8*x-4,x=0.5..3);Figura 4.17.a Raíces de polinomio cúbico.Dividiendo el polinomio cúbico por (x-1) se obtiene:Profesor Leopoldo Silva Bijit 20-01-2010