2. hét: Az alakváltozás fogalma, kis és nagy alakváltozások ...

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
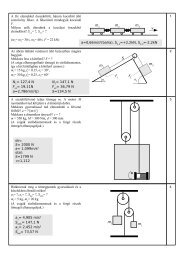
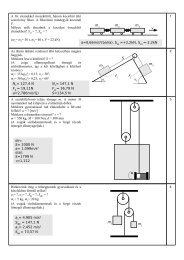
Kétdimenziós esetben az általános transzformáló összefüggések egyszerű skalár
kifejezésekkel is megadhatók, a gyakorlatban többnyire ezeket használják. Ilyenkor
trigonometriai átalakításokkal a kétszeres szögeket használják:
1 1
ε ′ x x = ( ε x x + ε yy ) + ( εx x − ε yy ) cos 2ϑ + εx y sin 2 ϑ,
2 2
1 1
ε ′ y y = ( ε x x + ε yy ) − ( εx x − ε yy ) cos 2ϑ − εx y sin 2 ϑ,
2 2
1
ε ′ x y = − ( εx x − ε yy ) sin 2ϑ + εx y cos 2 ϑ.
2
Behelyettesítve a megadott értékeket:
−3 ⎧1 1
� � ⎫
−3
ε ′ x x = 10 ⎨ ( − 0,75 + 0,5) + ( −0,75 − 0,5) cos70 − 0, 4sin 70 ⎬ = −0,7146 ⋅10
,
⎩2 2
⎭
−3 ⎧1 1
� � ⎫
−3
ε ′ y y = 10 ⎨ ( − 0,75 + 0,5) − ( −0,75 − 0,5) cos 70 + 0,4sin 70 ⎬ = 0, 4646⋅10 ,
⎩2 2
⎭
−3 ⎧ 1
� � ⎫
−3
ε ′ x y = 10 ⎨− ( −0,75 − 0,5) sin 70 − 0,4cos70 ⎬ = 0,4505 ⋅10
.
⎩ 2
⎭
A transzformáció helyessége a két különböző rendszerben számított alakváltozási
invariánsok összehasonlításával ellenőrizhető:
I′
( ε ) = ε + ε = − 0,00075 + 0,0005 = −0,00025,
1
x x y y
I′
( ε ′ ) = ε ′ + ε ′ = − 0,0007146 + 0,0004646 = −0,00025,
1
x x y y
ε ε −0,00075 −0,0004
I′
ε = = = − ⋅
x x x y
−7
2(
) 5,35 10 ,
ε y x ε y y −0,0004
0,0005
I′
′
ε′ ε′ −0,0007146
0,0004505
x x x y
−7
2(
ε ) = = = − 5,35 ⋅10
,
ε′ y x ε′
y y 0,0004505 0,0004646
A harmadik invariáns sík feladatok esetében mindig zérus.
Határozzuk meg ezek után a főnyúlások értékeit.
Kétdimenziós esetben a sajátértékfeladat karakterisztikus egyenlete másodfokú, így az ismert
megoldóképlet segítségével számíthatók a főnyúlások. A helyes indexszelésnél mindig
figyelembe kell vennünk, hogy most az eredeti másodrendű alakváltozás-mátrix egy sora és
egy oszlopa zérus, így minden esetben van egy darab zérusértékű főnyúlás. Ennek indexét a
sík feladatnál kapott eredmények előjelének figyelembevételével kell megadni.
A sík alakváltozási állapotnál alkalmazott megoldóképlet:
ε x x + ε y y
ε 1,3 = ±
2
2
⎛ εx x − ε y y ⎞ ⎧
2 −3
⎪− 0,75 + 0,5
⎜ ⎟ + εx y ⇒ε 1,3 = 10 ⎨ ±
⎝ 2 ⎠ ⎪ 2
⎩
2
⎛ −0,75 − 0,5 ⎞
⎫
2 ⎪
⎜ ⎟ + ( −0,
4)
⎬
⎝ 2 ⎠ ⎪⎭
A zérus érték figyelembevételével a főnyúlások:
−3 ε 1 = 0,617 ⋅10 , ε 2 = 0,
−3
ε 3 = −0,867 ⋅ 10 .
Ebben az esetben a fő-szögtorzulások értéke mindig zérus.
Az invariánsokat újból felhasználhatjuk ellenőrzésre:
I′
( ε ) = ε + ε + ε = 0,000617 + 0 − 0,000867 = −0,00025,
1 i 1 2 3
17
( )
I′
ε = ε ε + ε ε + ε ε = ⋅ − = − ⋅
−7
2( i ) 1 3 1 2 2 3 0,000617 0,000867 5,35 10 .