Soner Bekleric Title of Thesis: Nonlinear Prediction via Volterra Ser

4.3. NONLINEAR PREDICTION OF COMPLEX WAVEFORMS 54
Time (s)
0
0.2
0.4
0.6
Traces
20 40
(a)
Time (s)
0
0.2
0.4
0.6
Traces
20 40
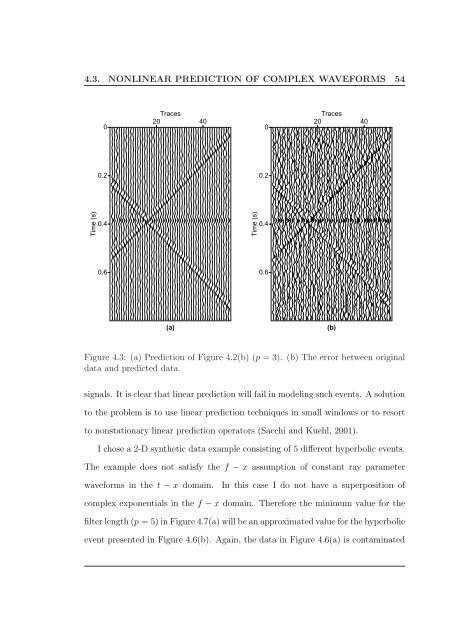
Figure 4.3: (a) Prediction of Figure 4.2(b) (p = 3). (b) The error between original
data and predicted data.
signals. It is clear that linear prediction will fail in modeling such events. A solution
to the problem is to use linear prediction techniques in small windows or to resort
to nonstationary linear prediction operators (Sacchi and Kuehl, 2001).
I chose a 2-D synthetic data example consisting of 5 different hyperbolic events.
The example does not satisfy the f − x assumption of constant ray parameter
waveforms in the t − x domain. In this case I do not have a superposition of
complex exponentials in the f − x domain. Therefore the minimum value for the
filter length (p = 5) in Figure 4.7(a) will be an approximated value for the hyperbolic
event presented in Figure 4.6(b). Again, the data in Figure 4.6(a) is contaminated
(b)