Hi-Res PDF - CRCnetBASE

Longitudinal Train Dynamics 249
If it is assumed that m 1 ¼ m 2 ; and that both surfaces are saturated, then the equation reduces to:
F c ¼ F s ð m cot f þ 1 Þ = ð 1 þ m 2 Þ ð9 : 13Þ
The other extreme ofpossibility is when there is no impending motion onthe sloping surface
due to the seatingofthe rod and wedge, the value assumed for m 1 is zero, Equation 9.10 reducing to:
F c ¼ F s tan f = ½ tan f 2 m 2 � ð9 : 14Þ
If the same analysis isrepeated for the unloading case, asimilar equation results,
F c ¼ F s tan f = ½ tan f þ m 2 � ð9 : 15Þ
At this point, it is convenient to define anew parameter, namely friction wedge factor, as follows:
Q ¼ F c = F s
ð 9 : 16Þ
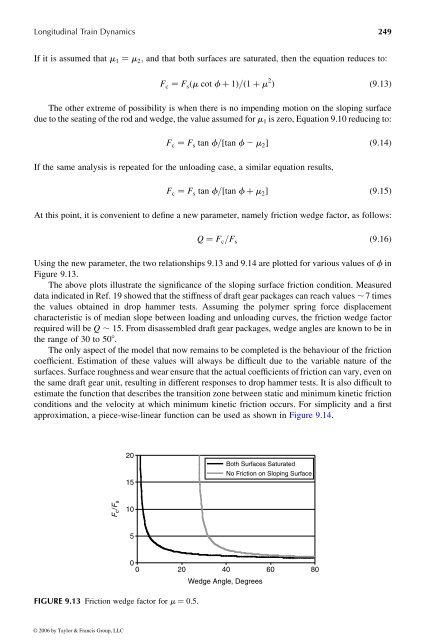
Using the new parameter, the two relationships 9.13 and 9.14 are plotted for various values of f in
Figure 9.13.
The above plots illustrate the significance of the sloping surface friction condition. Measured
data indicated in Ref. 19 showed that the stiffness of draft gear packages can reach values , 7times
the values obtained in drop hammer tests. Assuming the polymer spring force displacement
characteristic is of median slope between loading and unloading curves, the friction wedge factor
requiredwill be Q , 15. From disassembled draft gear packages, wedge angles are knowntobein
the range of 30 to 508 .
The only aspect of the modelthat now remains to be completed is the behaviour of the friction
coefficient. Estimation of these values will always be difficult due to the variable nature of the
surfaces. Surface roughness and wear ensurethat the actual coefficients of friction can vary, even on
the same draft gear unit, resulting in different responses to drop hammer tests. It is also difficult to
estimatethe function that describes the transition zone betweenstatic and minimum kinetic friction
conditions and the velocity at which minimum kinetic friction occurs. For simplicity and afirst
approximation, apiece-wise-linear function can be used as shown inFigure 9.14.
F c / F s
FIGURE 9.13 Friction wedge factor for m ¼ 0.5.
© 2006 by Taylor & Francis Group, LLC
20
15
10
5
Both Surfaces Saturated
0
0 20 40 60 80
Wedge Angle, Degrees
No Friction on Sloping Surface