Hi-Res PDF - CRCnetBASE

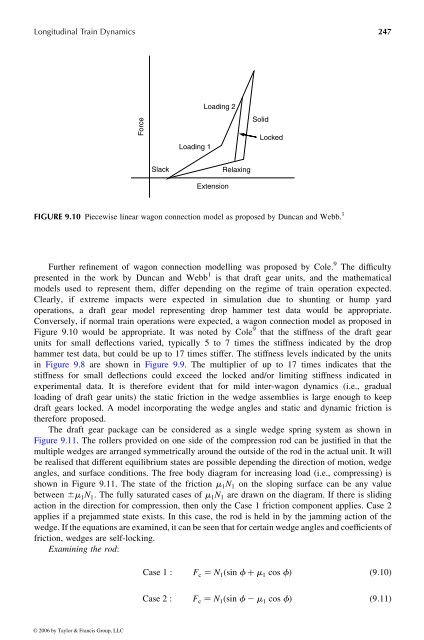
Longitudinal Train Dynamics 247
Force
Slack
Loading 1
Loading 2
Extension
Relaxing
Further refinement of wagon connection modelling was proposed by Cole. 9 The difficulty
presented in the work by Duncan and Webb 1 is that draft gear units, and the mathematical
models used to represent them, differ depending on the regime oftrain operation expected.
Clearly, if extreme impacts were expected in simulation due to shunting or hump yard
operations, a draft gear model representing drop hammer test data would be appropriate.
Conversely, if normal train operations were expected, awagon connection model asproposed in
Figure 9.10 would be appropriate. It was noted by Cole 9 that the stiffness ofthe draft gear
units for small deflections varied, typically 5to 7times the stiffness indicated by the drop
hammer test data, but could beupto17times stiffer. The stiffness levels indicated by the units
in Figure 9.8 are shown in Figure 9.9. The multiplier of up to 17 times indicates that the
stiffness for small deflections could exceed the locked and/or limiting stiffness indicated in
experimental data. It is therefore evident that for mild inter-wagon dynamics (i.e., gradual
loading of draft gear units) the static friction in the wedge assemblies is large enough to keep
draft gears locked. Amodel incorporating the wedge angles and static and dynamic friction is
therefore proposed.
The draft gear package can be considered as asingle wedge spring system as shown in
Figure 9.11. The rollers provided on one side of the compression rod can be justified in that the
multiplewedges are arranged symmetrically around the outside of the rod in the actual unit. It will
be realised that different equilibrium states are possible depending the direction of motion, wedge
angles, and surface conditions. The free body diagram for increasing load (i.e., compressing) is
shown in Figure 9.11. The state of the friction m 1 N 1 on the sloping surface can be any value
between ^ m 1 N 1 : The fully saturated cases of m 1 N 1 are drawn onthe diagram. If there issliding
action in the direction for compression, then only the Case 1friction component applies. Case 2
applies if aprejammed state exists. In this case, the rod is held in by the jamming action of the
wedge. If the equations are examined, it can be seen that for certainwedge angles and coefficients of
friction, wedges are self-locking.
Examining the rod:
Solid
Locked
FIGURE 9.10 Piecewise linear wagon connection model as proposed by Duncan and Webb. 1
© 2006 by Taylor & Francis Group, LLC
Case 1 : F c ¼ N 1 ð sin f þ m 1 cos f Þ ð9 : 10Þ
Case 2 : F c ¼ N 1 ð sin f 2 m 1 cos f Þ ð9 : 11Þ