Hi-Res PDF - CRCnetBASE

Longitudinal Train Dynamics 261
The grade also reduces the sum of the reactions of the wagon downward on the track. This
effect has implications for propulsion resistance equations that are dependent on vehicle weight.
However, the effect is small and, due to the inherent uncertainty in propulsions resistance
calculations, it can be safely ignored. Taking a1in 50 grade as an example, gives agrade angle
of 1.1468 .The cosine of this angle is 0.99979. The reduction in the sum of the normal reactions
for awagon on a1in 50 grade (or 2%) is therefore 0.02%.Grades are obtained from track plan and
section data. The grade force component must becalculated for each vehicle in the train and
updated each time step during simulation to account for train progression along the track section.
F . P ROPULSION R ESISTANCE
Propulsion resistance isusually defined as the sum of rolling resistance and air resistance. In most
cases, increased vehicle drag due to track curvature is considered separately. The variable shapes
and designs of rollingstock, and the complexity of aerodynamic drag, mean that the calculation
of rolling resistance is still dependent on empirical formulae. Typically, propulsion resistance is
expressedinanequation of the form of R ¼ A þ BV þ CV 2 : Hay presentsthe workofDavis which
identifies the term A as journal resistance dependent on both wagon mass and the number of axles,
an equation of the form R ¼ ax þ b ,giving in imperial units 1.3wn þ 29n ,where w is weight per
axle and n is the number of axles, is quoted inRef. 14. The second term is mainly dependent on
flanging friction and therefore the coefficient B is usually small (nonexistent in some empirical
formulae) and the third term isdependent on air resistance. The forms of propulsion resistance
equations used and the empirical factors selected vary between railway systems reflecting the use
of equations that more closely match the different types ofrollingstock and running speeds
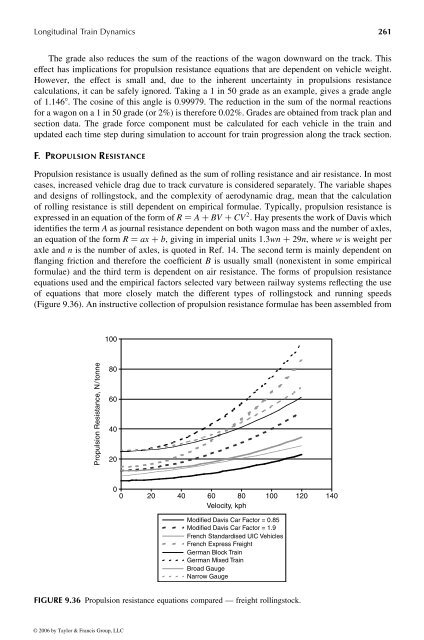
(Figure 9.36). An instructive collection of propulsion resistanceformulae has been assembled from
Propulsion Resistance, N/tonne
100
80
60
40
20
0
0 20 40 60 80 100 120 140
Velocity, kph
Modified Davis Car Factor =0.85
Modified Davis Car Factor =1.9
French Standardised UIC Vehicles
French Express Freight
German BlockTrain
German Mixed Train
Broad Gauge
Narrow Gauge
FIGURE 9.36 Propulsion resistance equations compared —freight rollingstock.
© 2006 by Taylor & Francis Group, LLC