Numerical Methods Course Notes Version 0.1 (UCSD Math 174, Fall ...

frag replacements
8.2. TRAPEZOIDAL RULE 101
uright
x i x i+1
lleft
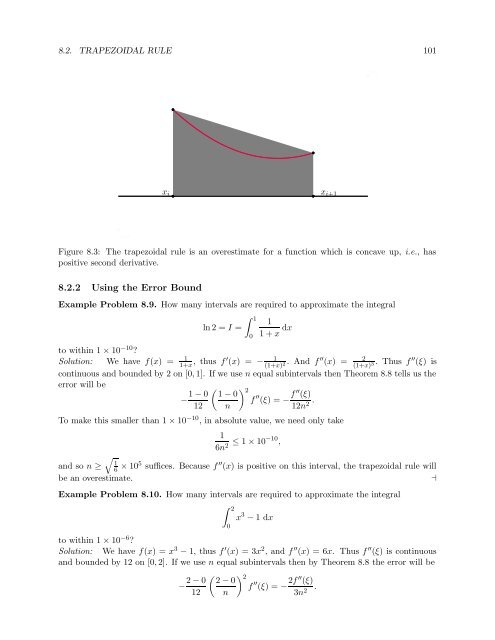
Figure 8.3: The trapezoidal rule is an overestimate for a function which is concave up, i.e., has
positive second derivative.
8.2.2 Using the Error Bound
Example Problem 8.9. How many intervals are required to approximate the integral
ln 2 = I =
∫ 1
0
1
1 + x dx
to within 1 × 10 −10 ?
Solution: We have f(x) = 1
1+x , thus f ′ (x) = − 1
(1+x)
. And f ′′ 2
(x) = 2 (1+x)
. Thus f ′′ (ξ) is
3
continuous and bounded by 2 on [0, 1]. If we use n equal subintervals then Theorem 8.8 tells us the
error will be
− 1 − 0 ( ) 1 − 0 2
f ′′ (ξ) = − f ′′ (ξ)
12 n
12n 2 .
To make this smaller than 1 × 10 −10 , in absolute value, we need only take
√
1
1
6n 2 ≤ 1 × 10−10 ,
and so n ≥
6 × 105 suffices. Because f ′′ (x) is positive on this interval, the trapezoidal rule will
be an overestimate.
⊣
Example Problem 8.10. How many intervals are required to approximate the integral
∫ 2
0
x 3 − 1 dx
to within 1 × 10 −6 ?
Solution: We have f(x) = x 3 − 1, thus f ′ (x) = 3x 2 , and f ′′ (x) = 6x. Thus f ′′ (ξ) is continuous
and bounded by 12 on [0, 2]. If we use n equal subintervals then by Theorem 8.8 the error will be
− 2 − 0 ( ) 2 − 0 2
f ′′ (ξ) = − 2f ′′ (ξ)
12 n
3n 2 .