Numerical Methods Course Notes Version 0.1 (UCSD Math 174, Fall ...

frag replacements
10.1. ELEMENTARY METHODS 127
10000
truncation
roundoff
total error
1000
100
10
1
0.1
0.01
1e-07 1e-06 1e-05 0.0001 0.001 0.01
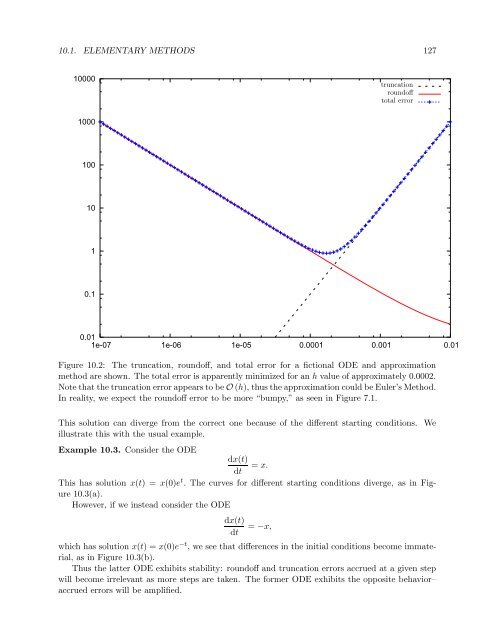
Figure 10.2: The truncation, roundoff, and total error for a fictional ODE and approximation
method are shown. The total error is apparently minimized for an h value of approximately 0.0002.
Note that the truncation error appears to be O (h), thus the approximation could be Euler’s Method.
In reality, we expect the roundoff error to be more “bumpy,” as seen in Figure 7.1.
This solution can diverge from the correct one because of the different starting conditions. We
illustrate this with the usual example.
Example 10.3. Consider the ODE
dx(t)
= x.
dt
This has solution x(t) = x(0)e t . The curves for different starting conditions diverge, as in Figure
10.3(a).
However, if we instead consider the ODE
dx(t)
dt
= −x,
which has solution x(t) = x(0)e −t , we see that differences in the initial conditions become immaterial,
as in Figure 10.3(b).
Thus the latter ODE exhibits stability: roundoff and truncation errors accrued at a given step
will become irrelevant as more steps are taken. The former ODE exhibits the opposite behavior–
accrued errors will be amplified.