reverse engineering – recent advances and applications - OpenLibra

More documents

Recommendations

Info

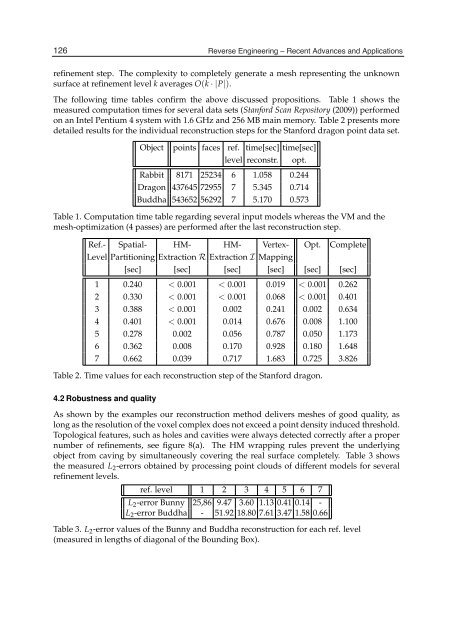
126 Reverse Engineering – Recent Advances and Applications 10 Will-be-set-by-IN-TECH refinement step. The complexity to completely generate a mesh representing the unknown surface at refinement level k averages O(k ·|P|). The following time tables confirm the above discussed propositions. Table 1 shows the measured computation times for several data sets (Stanford Scan Repository (2009)) performed on an Intel Pentium 4 system with 1.6 GHz and 256 MB main memory. Table 2 presents more detailed results for the individual reconstruction steps for the Stanford dragon point data set. Object points faces ref. time[sec] time[sec] level reconstr. opt. Rabbit 8171 25234 6 1.058 0.244 Dragon 437645 72955 7 5.345 0.714 Buddha 543652 56292 7 5.170 0.573 Table 1. Computation time table regarding several input models whereas the VM and the mesh-optimization (4 passes) are performed after the last reconstruction step. Ref.- Spatial- HM- HM- Vertex- Opt. Complete Level Partitioning Extraction R Extraction I Mapping [sec] [sec] [sec] [sec] [sec] [sec] 1 0.240 < 0.001 < 0.001 0.019 < 0.001 0.262 2 0.330 < 0.001 < 0.001 0.068 < 0.001 0.401 3 0.388 < 0.001 0.002 0.241 0.002 0.634 4 0.401 < 0.001 0.014 0.676 0.008 1.100 5 0.278 0.002 0.056 0.787 0.050 1.173 6 0.362 0.008 0.170 0.928 0.180 1.648 7 0.662 0.039 0.717 1.683 0.725 3.826 Table 2. Time values for each reconstruction step of the Stanford dragon. 4.2 Robustness and quality As shown by the examples our reconstruction method delivers meshes of good quality, as long as the resolution of the voxel complex does not exceed a point density induced threshold. Topological features, such as holes and cavities were always detected correctly after a proper number of refinements, see figure 8(a). The HM wrapping rules prevent the underlying object from caving by simultaneously covering the real surface completely. Table 3 shows the measured L2-errors obtained by processing point clouds of different models for several refinement levels. ref. level 1 2 3 4 5 6 7 L2-error Bunny 25,86 9.47 3.60 1.13 0.41 0.14 - L2-error Buddha - 51.92 18.80 7.61 3.47 1.58 0.66 Table 3. L2-error values of the Bunny and Buddha reconstruction for each ref. level (measured in lengths of diagonal of the Bounding Box).
Surface Reconstruction from Unorganized 3D Point Clouds Surface Reconstruction from Unorganized 3D Point Clouds 11 (a) (b) Fig. 8. (a) correctly detected holes in the bunny model, (b) fragmentation of the mesh due to lacking density of point cloud. In case the voxel refinement level exceeds a specific bound imposed by sampling density, the resulting mesh may be incomplete in some areas, due to empty voxels, see figure 8(b). If a very fine mesh is desired, one can fix the topology at a coarser level and apply subdivision and vertex mapping in consecutive steps. 5. Experimental reconstruction of environmental point data The exploration of point data sets, like environmental LiDaR data, is a challenging problem of current interest. In contrast to the point clouds obtained from stationary scanning devices, data complexity is increased by e.g., noise, occlusion, alternating sample density and overlapping samples. Despite of the high scanning resolution, additional undersampling may occur at small and fractured artifacts like fences and leaves of trees. These are only some problems immanent to the reconstruction of surfaces from unorganized environmental point clouds. We have applied our method to environmental point clouds in order to analyse the effects of the aforementioned influence factors on our proposed reconstruction approach. In this context we have performed some experiments on environmental input data generated by tripod mounted LiDaR scanners. Figure 10(a) shows a point cloud of a water tower located at the UC Davis, CA, USA. It consists of about 4.3 million points and features complex environmental structures like buildings and trees. Figure 10(b) shows the corresponding reconstruction after 10 steps. The generated mesh exhibiting about 300 thousand faces took 23 seconds on an Intel Core2 Duo system with 4GB RAM to finish. Another example is presented in figure 11. It shows the final surface representation (215 thousand faces) of a slope with parts of a building and some vegetation. The underlying point cloud has 3.8 million points. The reconstruction finished at level 9 after 24 second. The reconstructed mesh features holes and cracks at those areas at which the resolution lacks in density. Environmental point clouds by nature are large (consisting of up to several million points) and feature high complexity. The experiments showed that our reconstruction approach is capable of producing reliable representations even in cases in which the point clouds are not optimally conditioned. However, the reconstruction lacks at some regions in which the point density does not exhibit the required/satisfied resolution. Despite of this fact the introduced method 127
Page 1 and 2:
REVERSE ENGINEERING - RECENT ADVANC
Page 5 and 6:
Contents Preface IX Part 1 Software
Page 9 and 10:
Preface Introduction In the recent
Page 11 and 12:
Preface XI and con’s related to t
Page 13 and 14:
Preface XIII the step-by-step appli
Page 17:
Part 1 Software Reverse Engineering
Page 20 and 21:
4 Reverse Engineering - Recent Adva
Page 22 and 23:
Page 24 and 25:
Page 26 and 27:
10 Reverse Engineering - Recent Adv
Page 28 and 29:
Page 30 and 31:
Page 32 and 33:
Page 34 and 35:
Page 36 and 37:
Page 38 and 39:
Page 40 and 41:
Page 42 and 43:
Page 44 and 45:
Page 46 and 47:
Page 48 and 49:
Page 50 and 51:
Page 52 and 53:
Page 54 and 55:
Page 56 and 57:
Page 58 and 59:
Page 60 and 61:
Page 62 and 63:
Page 64 and 65:
Page 66 and 67:
Page 68 and 69:
Page 70 and 71:
Page 72 and 73:
Page 74 and 75:
58 2. Model driven architecture: An
Page 76 and 77:
Page 78 and 79:
62 Fig. 1. Model, metamodels and tr
Page 80 and 81:
Page 82 and 83:
Page 84 and 85:
Page 86 and 87:
Page 88 and 89:
Page 90 and 91:
Page 92 and 93: 76 Reverse Engineering - Recent Adv
Page 116 and 117: 100 Reverse Engineering - Recent Ad
Page 124 and 125: 108 Table 1. Number of smoothers an
Page 133 and 134: 1. Introduction 60 Surface Reconstr
Page 135 and 136: Surface Reconstruction from Unorgan
Page 141: Surface Reconstruction from Unorgan
Page 149 and 150: 1. Introduction A Systematic Approa
Page 151 and 152: A Systematic Approach for Geometric
Page 177 and 178: A Review on Shape Engineering and D
Page 193 and 194:
A Review on Shape Engineering and D
Page 195 and 196:
Page 197 and 198:
Page 199 and 200:
Page 201 and 202:
Page 203 and 204:
Integrating Reverse Engineering and
Page 205 and 206:
Page 207 and 208:
Page 209 and 210:
Page 211 and 212:
Page 213 and 214:
Page 215 and 216:
Page 217 and 218:
Page 219 and 220:
Page 221 and 222:
Page 223 and 224:
Page 225 and 226:
Page 227 and 228:
Page 229 and 230:
Page 231:
Part 3 Reverse Engineering in Medic
Page 234 and 235:
218 Reverse Engineering - Recent Ad
Page 236 and 237:
Page 238 and 239:
Page 240 and 241:
Page 242 and 243:
Page 244 and 245:
Page 246 and 247:
Page 248 and 249:
Page 250 and 251:
Page 252 and 253:
Page 254 and 255:
238 5. Summary and discussions Reve
Page 256 and 257:
Page 258 and 259:
Page 260 and 261:
Page 262 and 263:
Page 264 and 265:
Page 266 and 267:
Page 268 and 269:
Page 270 and 271:
Page 272 and 273:
Page 274 and 275:
Page 276 and 277:
Page 278 and 279:
Page 280 and 281:
Page 282 and 283:
Page 284 and 285:
268 Fig. 6. A closed polygon mesh r
Page 286 and 287:
Page 288 and 289:
272 3. Results Reverse Engineering
Page 290 and 291:
Page 292:
show all

reverse engineering – recent advances and applications - OpenLibra

Create successful ePaper yourself

Delete template?

Save as template?