Subsampling estimates of the Lasso distribution.

60 Numerical results
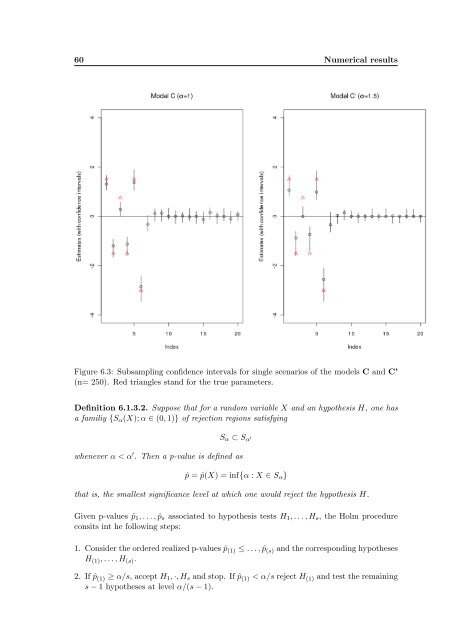
Figure 6.3: Subsampling confidence intervals for single scenarios of the models C and C’
(n= 250). Red triangles stand for the true parameters.
Definition 6.1.3.2. Suppose that for a random variable X and an hypothesis H, one has
a familiy {S α (X); α ∈ (0, 1)} of rejection regions satisfying
S α ⊂ S α ′
whenever α < α ′ . Then a p-value is defined as
ˆp = ˆp(X) = inf{α : X ∈ S α }
that is, the smallest significance level at which one would reject the hypothesis H.
Given p-values ˆp 1 , . . . , ˆp s associated to hypothesis tests H 1 , . . . , H s , the Holm procedure
consits int he following steps:
1. Consider the ordered realized p-values ˆp (1) ≤ . . . , ˆp (s) and the corresponding hypotheses
H (1) , . . . , H (s) .
2. If ˆp (1) ≥ α/s, accept H 1 , ·, H s and stop. If ˆp (1) < α/s reject H (1) and test the remaining
s − 1 hypotheses at level α/(s − 1).