- Page 2:
International Series in Operations
- Page 5 and 6:
Editors Jeff Kennington Eli Olinick
- Page 7 and 8:
vi Preface assistance. The work of
- Page 9 and 10:
viii Contents 3.4.1 Experiments to
- Page 11 and 12:
x Contents 8.3.2 The Solution Proce
- Page 13 and 14:
xii Contents References . . . . . .
- Page 16 and 17:
List of Contributors Khaldoun Al Ag
- Page 18:
List of Contributors xvii Nitin Sal
- Page 22 and 23:
Chapter 1 Introduction to Optimizat
- Page 24 and 25:
1 Introduction to Optimization in W
- Page 26 and 27:
1 Introduction to Optimization in W
- Page 29 and 30:
Part I Background
- Page 31 and 32:
10 Dinesh Rajan The goal of this ch
- Page 33 and 34:
12 Dinesh Rajan The source encoder
- Page 35 and 36:
14 Dinesh Rajan ping (FH) CDMA, and
- Page 37 and 38: 16 Dinesh Rajan of SNR is given in
- Page 39 and 40: 18 Dinesh Rajan 2.3 Information The
- Page 41 and 42: 20 Dinesh Rajan Perror ≤ e −nE
- Page 43 and 44: 22 Dinesh Rajan For instance, for t
- Page 45 and 46: 24 Dinesh Rajan 2.4.1 Block Codes I
- Page 47 and 48: 26 Dinesh Rajan B(z) = 1 � (1 + z
- Page 49 and 50: 28 Dinesh Rajan layers. Two of the
- Page 51 and 52: 30 Dinesh Rajan nel can support a p
- Page 53 and 54: 32 Dinesh Rajan 2.5.2 Physical laye
- Page 55 and 56: 34 Dinesh Rajan matched filter for
- Page 57 and 58: 36 Dinesh Rajan codes) leads to bet
- Page 59 and 60: 38 Dinesh Rajan a length N Inverse
- Page 61 and 62: 40 Dinesh Rajan the transmission of
- Page 63 and 64: 42 Dinesh Rajan setting, a node may
- Page 65 and 66: 44 Dinesh Rajan weighting of the si
- Page 67 and 68: 46 Dinesh Rajan 29. Oestges, C., Cl
- Page 69 and 70: 48 K. V. S. Hari terrain of operati
- Page 71 and 72: 50 K. V. S. Hari fading is calculat
- Page 73 and 74: 52 K. V. S. Hari terms have been pr
- Page 75 and 76: 54 K. V. S. Hari Fig. 3.1 Normalize
- Page 77 and 78: 56 K. V. S. Hari Table 3.3 Impulse
- Page 79 and 80: 58 K. V. S. Hari where m antennas a
- Page 81 and 82: 60 K. V. S. Hari 3.5.2.4 Dominant R
- Page 83 and 84: 62 K. V. S. Hari March, 1984-13 Sep
- Page 85 and 86: 64 K. V. S. Hari 47. Van Rees, J.:
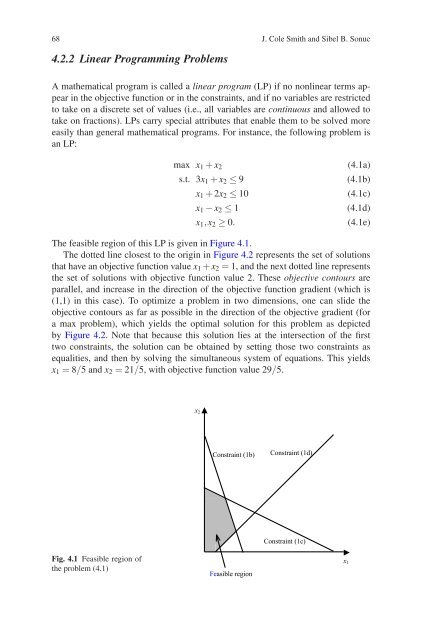
- Page 87: 66 J. Cole Smith and Sibel B. Sonuc
- Page 91 and 92: 70 J. Cole Smith and Sibel B. Sonuc
- Page 93 and 94: 72 J. Cole Smith and Sibel B. Sonuc
- Page 95 and 96: 74 J. Cole Smith and Sibel B. Sonuc
- Page 97 and 98: 76 J. Cole Smith and Sibel B. Sonuc
- Page 99 and 100: 78 J. Cole Smith and Sibel B. Sonuc
- Page 101 and 102: 80 J. Cole Smith and Sibel B. Sonuc
- Page 103 and 104: 82 J. Cole Smith and Sibel B. Sonuc
- Page 105 and 106: 84 J. Cole Smith and Sibel B. Sonuc
- Page 107 and 108: 86 J. Cole Smith and Sibel B. Sonuc
- Page 109 and 110: 88 J. Cole Smith and Sibel B. Sonuc
- Page 111 and 112: 90 J. Cole Smith and Sibel B. Sonuc
- Page 113 and 114: 92 J. Cole Smith and Sibel B. Sonuc
- Page 115 and 116: 94 J. Cole Smith and Sibel B. Sonuc
- Page 117 and 118: 96 J. Cole Smith and Sibel B. Sonuc
- Page 120: Part II Optimization Problems for N
- Page 123 and 124: 102 Eli Olinick carrying capacity.
- Page 125 and 126: 104 Eli Olinick 93 85 160 16 38 21
- Page 127 and 128: 106 Eli Olinick Amaldi et al. [7] p
- Page 129 and 130: 108 Eli Olinick levels (possibly le
- Page 131 and 132: 110 Eli Olinick gmℓ ∑ ∑ m∈M
- Page 133 and 134: 112 Eli Olinick Using bk to denote
- Page 135 and 136: 114 Eli Olinick 5.3.5 Additional De
- Page 137 and 138: 116 Eli Olinick capacity, provide n
- Page 139 and 140:
118 Eli Olinick ficult optimization
- Page 141 and 142:
120 Eli Olinick and-bound so that t
- Page 143 and 144:
122 Eli Olinick solution times. Cai
- Page 145 and 146:
124 Eli Olinick 27. Glover, F.: Tab
- Page 148 and 149:
Chapter 6 Optimization Based WLAN M
- Page 150 and 151:
6 Optimization Based WLAN Modeling
- Page 152 and 153:
6 Optimization Based WLAN Modeling
- Page 154 and 155:
6 Optimization Based WLAN Modeling
- Page 156 and 157:
6 Optimization Based WLAN Modeling
- Page 158 and 159:
6 Optimization Based WLAN Modeling
- Page 160 and 161:
6 Optimization Based WLAN Modeling
- Page 162 and 163:
6 Optimization Based WLAN Modeling
- Page 164 and 165:
6 Optimization Based WLAN Modeling
- Page 166 and 167:
6 Optimization Based WLAN Modeling
- Page 168 and 169:
Chapter 7 Spectrum Auctions Karla H
- Page 170 and 171:
7 Spectrum Auctions 149 full value.
- Page 172 and 173:
7 Spectrum Auctions 151 also decide
- Page 174 and 175:
7 Spectrum Auctions 153 disclosed t
- Page 176 and 177:
7 Spectrum Auctions 155 focused on
- Page 178 and 179:
7 Spectrum Auctions 157 bidders to
- Page 180 and 181:
7 Spectrum Auctions 159 in the regi
- Page 182 and 183:
7 Spectrum Auctions 161 we suggest
- Page 184 and 185:
7 Spectrum Auctions 163 pays, since
- Page 186 and 187:
7 Spectrum Auctions 165 prior round
- Page 188 and 189:
7 Spectrum Auctions 167 and constra
- Page 190 and 191:
7 Spectrum Auctions 169 lem has sup
- Page 192 and 193:
7 Spectrum Auctions 171 bidder on a
- Page 194 and 195:
7 Spectrum Auctions 173 some discus
- Page 196 and 197:
7 Spectrum Auctions 175 21. Dunford
- Page 198 and 199:
Chapter 8 The Design of Partially S
- Page 200 and 201:
8 The Design of Partially Survivabl
- Page 202 and 203:
8 The Design of Partially Survivabl
- Page 204 and 205:
8 The Design of Partially Survivabl
- Page 206 and 207:
8 The Design of Partially Survivabl
- Page 208 and 209:
8 The Design of Partially Survivabl
- Page 210 and 211:
8 The Design of Partially Survivabl
- Page 212 and 213:
8 The Design of Partially Survivabl
- Page 214 and 215:
8 The Design of Partially Survivabl
- Page 216 and 217:
8 The Design of Partially Survivabl
- Page 219 and 220:
Part III Optimization Problems in A
- Page 221 and 222:
200 Khaldoun Al Agha and Steven Mar
- Page 223 and 224:
202 Khaldoun Al Agha and Steven Mar
- Page 225 and 226:
204 Khaldoun Al Agha and Steven Mar
- Page 227 and 228:
206 Khaldoun Al Agha and Steven Mar
- Page 229 and 230:
208 Khaldoun Al Agha and Steven Mar
- Page 231 and 232:
210 Khaldoun Al Agha and Steven Mar
- Page 233 and 234:
212 Khaldoun Al Agha and Steven Mar
- Page 235 and 236:
214 Khaldoun Al Agha and Steven Mar
- Page 237 and 238:
216 Khaldoun Al Agha and Steven Mar
- Page 240 and 241:
Chapter 10 Compact Integer Programm
- Page 242 and 243:
10 Integer Programming Models for P
- Page 244 and 245:
10 Integer Programming Models for P
- Page 246 and 247:
10 Integer Programming Models for P
- Page 248 and 249:
10 Integer Programming Models for P
- Page 250 and 251:
10 Integer Programming Models for P
- Page 252 and 253:
10 Integer Programming Models for P
- Page 254 and 255:
10 Integer Programming Models for P
- Page 256 and 257:
10 Integer Programming Models for P
- Page 258 and 259:
10 Integer Programming Models for P
- Page 260 and 261:
10 Integer Programming Models for P
- Page 262 and 263:
10 Integer Programming Models for P
- Page 264 and 265:
10 Integer Programming Models for P
- Page 266 and 267:
10 Integer Programming Models for P
- Page 268 and 269:
Chapter 11 Improving Network Connec
- Page 270 and 271:
11 Improving Network Connectivity i
- Page 272 and 273:
11 Improving Network Connectivity i
- Page 274 and 275:
11 Improving Network Connectivity i
- Page 276 and 277:
11 Improving Network Connectivity i
- Page 278 and 279:
11 Improving Network Connectivity i
- Page 280 and 281:
11 Improving Network Connectivity i
- Page 282 and 283:
11 Improving Network Connectivity i
- Page 284 and 285:
11 Improving Network Connectivity i
- Page 286 and 287:
11 Improving Network Connectivity i
- Page 288:
11 Improving Network Connectivity i
- Page 292 and 293:
Chapter 12 Simulation-Based Methods
- Page 294 and 295:
12 Simulation-Based Methods for Net
- Page 296 and 297:
12 Simulation-Based Methods for Net
- Page 298 and 299:
12 Simulation-Based Methods for Net
- Page 300 and 301:
12 Simulation-Based Methods for Net
- Page 302 and 303:
12 Simulation-Based Methods for Net
- Page 304 and 305:
12 Simulation-Based Methods for Net
- Page 306 and 307:
12 Simulation-Based Methods for Net
- Page 308 and 309:
12 Simulation-Based Methods for Net
- Page 310 and 311:
12 Simulation-Based Methods for Net
- Page 312 and 313:
12 Simulation-Based Methods for Net
- Page 314:
12 Simulation-Based Methods for Net
- Page 317 and 318:
296 Hang Jin and Li Guo formance in
- Page 319 and 320:
298 Hang Jin and Li Guo (ISI) as lo
- Page 321 and 322:
300 Hang Jin and Li Guo ARQ (HARQ)
- Page 323 and 324:
302 Hang Jin and Li Guo 13.3 Radio
- Page 325 and 326:
304 Hang Jin and Li Guo Table 13.2
- Page 327 and 328:
306 Hang Jin and Li Guo is transmit
- Page 329 and 330:
308 Hang Jin and Li Guo uplink powe
- Page 331 and 332:
310 Hang Jin and Li Guo The link ad
- Page 333 and 334:
312 Hang Jin and Li Guo where ρ mi
- Page 335 and 336:
314 Hang Jin and Li Guo 13.4.4.3 Ex
- Page 337 and 338:
316 Hang Jin and Li Guo Fig. 13.9 P
- Page 339 and 340:
318 Hang Jin and Li Guo 1. Guarante
- Page 342 and 343:
Chapter 14 Cross Layer Scheduling i
- Page 344 and 345:
14 Cross Layer Scheduling in Wirele
- Page 346 and 347:
14 Cross Layer Scheduling in Wirele
- Page 348 and 349:
14 Cross Layer Scheduling in Wirele
- Page 350 and 351:
14 Cross Layer Scheduling in Wirele
- Page 352 and 353:
14 Cross Layer Scheduling in Wirele
- Page 354 and 355:
14 Cross Layer Scheduling in Wirele
- Page 356 and 357:
14 Cross Layer Scheduling in Wirele
- Page 358 and 359:
14 Cross Layer Scheduling in Wirele
- Page 360 and 361:
14 Cross Layer Scheduling in Wirele
- Page 362 and 363:
14 Cross Layer Scheduling in Wirele
- Page 364 and 365:
14 Cross Layer Scheduling in Wirele
- Page 366 and 367:
14 Cross Layer Scheduling in Wirele
- Page 368 and 369:
14 Cross Layer Scheduling in Wirele
- Page 370 and 371:
14 Cross Layer Scheduling in Wirele
- Page 372 and 373:
14 Cross Layer Scheduling in Wirele
- Page 374 and 375:
Chapter 15 Major Trends in Cellular
- Page 376 and 377:
15 Major Trends in Cellular Network
- Page 378 and 379:
15 Major Trends in Cellular Network
- Page 380 and 381:
15 Major Trends in Cellular Network
- Page 382 and 383:
15 Major Trends in Cellular Network
- Page 384 and 385:
15 Major Trends in Cellular Network
- Page 386 and 387:
15 Major Trends in Cellular Network
- Page 388 and 389:
15 Major Trends in Cellular Network
- Page 390 and 391:
15 Major Trends in Cellular Network
- Page 392 and 393:
15 Major Trends in Cellular Network
- Page 394:
15 Major Trends in Cellular Network