CLASE SEMANA 09

RAÍCES DE UN POLINOMIO
A > 0 i < 0
2. Teorema de Cardano – Viette
x 1 x 2
Teorema de paridad raíces:
x 1 = x
Teorema 1
2
En el polinomio. P(x) = ax 2 + bx + c; a ≠ 0 de raíces.
x 1 = x 2 x 1 = x 2
x 1 ; x 2 .
• Suma de raíces: x 1 + x 2 = – b a
y y
• Producto de raíces: x 1 . x 2 = c a
A < 0 i < 0
• De la identidad de Legendre se tiene:
(x 1
+ x 2
) 2 – (x 1
– x 2
) 2 = 4x 1
x 2
IV. polInomIo de teRceR gRado
3. Teorema (Análisis de las raíces)
Del polinomio P(x) = ax 2 + bx + c; a ≠ 0 de
coeficientes reales, raíces x 1 y x 2 y discriminante
i = b 2 – 4ac se cumple:
Mediante el teorema fundamental del álgebra y su
colorario, el polinomio tiene 3 raíces, denotaremos por
x 1 ; x 2 , x 3 . En tal caso el polinomio factorizado será:
P(x) = A(x – x 1 )(x – x 2 )(x – x 3 ); A ≠ 0
• Si: i > 0 ⇔ x 1 ; x 2 ∈ x 1 ≠ x 2
Equivalente a:
• Si: i = 0 ⇔ x 1 ; x 2 ∈ x 1 = x 2
P(x) = x 3 – (x 1 + x 2 + x 3 )x 2 + (x 1 x 2 + x 1 x 3 +x 2 x 3 )x –
• Si: i < 0 ⇔ x 1 ; x 2 ∉ x 1 = x 2
x 1
x 2
x 3
de donde se observa:
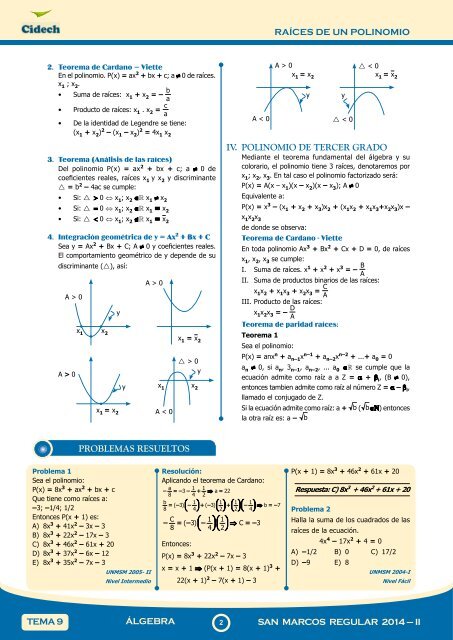
4. Integración geométrica de y = Ax 2 + Bx + C Teorema de Cardano - Viette
Sea y = Ax 2 + Bx + C; A ≠ 0 y coeficientes reales. En toda polinomio Ax 3 + Bx 2 + Cx + D = 0, de raíces
El comportamiento geométrico de y depende de su
x 1
, x 2
, x 3
se cumple:
discriminante (i), así:
I. Suma de raíces. x 1 + x 2 + x 3 = – B A
A > 0
II. Suma de productos binarios de las raíces:
x 1 x 2 + x 1 x 3 + x 2 x 3 = C
A > 0
A
III. Producto de las raíces:
x 1 = x Si la ecuación admite como raíz: a + b ( b∈) entonces
2 A < 0
la otra raíz es: a – b
y
x 1 x 2 x 3 = – D A
Sea el polinomio:
P(x) = anx n + a
i > 0
n–1
x n–1 + a n–2
x n–2 + ...+ a 0
= 0
a
A > 0
y
n ≠ 0, si a n , 3 n–1 , a n–2 , ... a 0 ∈ se cumple que la
ecuación admite como raíz a a Z = a + b i , (B ≠ 0),
y x 1 x 2
entonces tambien admite como raíz al número Z = a – b i ,
llamado el conjugado de Z.
pRoBlemas Resueltos
Problema 1
Sea el polinomio:
P(x) = 8x 3 + ax 2 + bx + c
Que tiene como raíces a:
–3; –1/4; 1/2
Entonces P(x + 1) es:
A) 8x 3 + 41x 2 – 3x – 3
B) 8x 3 + 22x 2 – 17x – 3
C) 8x 3 + 46x 2 – 61x + 20
D) 8x 3 + 37x 2 – 6x – 12
E) 8x 3 + 35x 2 – 7x – 3
UNMSM 2005- II
Nivel Intermedio
Resolución:
Aplicando el teorema de Cardano:
a 1 1
– =– 3 – + ⇒ a = 22
8 4 2
b ⎛ 1⎞ ⎛1⎞ ⎛1⎞⎛ 1⎞ = (– 3) ⎜ – ⎟ + (– 3) ⎜ ⎟ + ⎜ ⎟⎜ – ⎟ ⇒ b =– 7
8 ⎝ 4⎠ ⎝2⎠ ⎝2⎠⎝ 4⎠
C ⎛ 1⎞⎛1⎞ – = (– 3) ⎜ – ⎟⎜ ⎟⇒
C =– 3
8 ⎝ 4⎠⎝2⎠
Entonces:
P(x) = 8x 3 + 22x 2 – 7x – 3
x = x + 1 ⇒ (P(x + 1) = 8(x + 1) 3 +
22(x + 1) 2 – 7(x + 1) – 3
P(x + 1) = 8x 3 + 46x 2 + 61x + 20
Respuesta: C) 8x 3 + 46x 2 + 61x + 20
Problema 2
Halla la suma de los cuadrados de las
raíces de la ecuación.
4x 4 – 17x 2 + 4 = 0
A) –1/2 B) 0 C) 17/2
D) –9 E) 8
UNMSM 2004-I
Nivel Fácil
TEma 9
áLGEbra
2
2 san marcos rEGULar 2014 – II