Evolution and Optimum Seeking

More documents

Recommendations

Info

Test Problems for the Second Part of the Strategy Comparison 341 Figure A.14: Graphical representation of Problem 2.21 for n =2 F (x) ==2 4 6 8 10= Powell also ended the search without making any signi cant improvement on the initial condition. Both the simplex method of Nelder and Mead and the complex method of Box also had trouble in the minimum search in their cases the initially constructed simplex or complex collapsed long before reaching the minimum, again near one of the corners. Problem 2.22 Objective function: Minimum: Start: F (x) = nX i=1 jxij + nY i=1 jxij for n =5 x i =0 for i = 1(1)n F (x )=0 x (0) i =10 for i = 1(1)n F (x (0) ) = 100050 The simplex and complex methods did not nd the minimum. As in the previous Problem 2.21, this is due to the sharply pointed corners of the contours. The variable metric strategy also nally got stuck at one of these corners and converged no further. In this case the discontinuity in the partial derivatives of the objective function at the corners is to blame for its failure.
342 Appendix A Problem 2.23 Objective function: Minimum: Figure A.15: Graphical representation of Problem 2.22 for n =2 F (x) ==3 8 15 24 35 48 63 80 99= F (x) = nX i=1 x 10 i for n =5 x i =0 for i =1(1)n F (x )=0 Figure A.16: Graphical representation of Problem 2.23 for n =2 F (x) ==2 10 4 10 6 10 8 10 10 10 =
Page 1:
Evolution and Optimum Seeking Hans-
Page 4 and 5:
vi Multiple Data) machines with man
Page 6 and 7:
viii 3.2.1.6 Complex Strategy of Bo
Page 9 and 10:
Chapter 1 Introduction There is sca
Page 11 and 12:
Introduction 3 simple matter to col
Page 13 and 14:
Chapter 2 Problems and Methods of O
Page 15 and 16:
Particular Problems and Methods of
Page 17 and 18:
Page 19 and 20:
Page 21 and 22:
Page 23 and 24:
Page 25 and 26:
Page 27 and 28:
Other Special Cases 19 with expecta
Page 29 and 30:
Other Special Cases 21 parts of the
Page 31 and 32:
Chapter 3 Hill climbing Strategies
Page 33 and 34:
One Dimensional Strategies 25 then
Page 35 and 36:
One Dimensional Strategies 27 Even
Page 37 and 38:
One Dimensional Strategies 29 The b
Page 39 and 40:
One Dimensional Strategies 31 F(x)
Page 41 and 42:
One Dimensional Strategies 33 For t
Page 43 and 44:
One Dimensional Strategies 35 It is
Page 45 and 46:
One Dimensional Strategies 37 F P F
Page 47 and 48:
Multidimensional Strategies 39 the
Page 49 and 50:
Multidimensional Strategies 41 asch
Page 51 and 52:
Multidimensional Strategies 43 e 2
Page 53 and 54:
Multidimensional Strategies 45 Step
Page 55 and 56:
Multidimensional Strategies 47 Numb
Page 57 and 58:
Multidimensional Strategies 49 wher
Page 59 and 60:
Page 61 and 62:
Multidimensional Strategies 53 Numb
Page 63 and 64:
Multidimensional Strategies 55 The
Page 65 and 66:
Multidimensional Strategies 57 Anum
Page 67 and 68:
Page 69 and 70:
Multidimensional Strategies 61 Iter
Page 71 and 72:
Multidimensional Strategies 63 (If
Page 73 and 74:
Multidimensional Strategies 65 eval
Page 75 and 76:
Multidimensional Strategies 67 The
Page 77 and 78:
Multidimensional Strategies 69 devi
Page 79 and 80:
Multidimensional Strategies 71 spec
Page 81 and 82:
Multidimensional Strategies 73 othe
Page 83 and 84:
Multidimensional Strategies 75 anot
Page 85 and 86:
Multidimensional Strategies 77 3.2.
Page 87 and 88:
Page 89 and 90:
Multidimensional Strategies 81 Brow
Page 91 and 92:
Multidimensional Strategies 83 (197
Page 93 and 94:
Multidimensional Strategies 85 meth
Page 95 and 96:
Chapter 4 Random Strategies One gro
Page 97 and 98:
Random Strategies 89 parts is taken
Page 99 and 100:
Random Strategies 91 Pardalos and R
Page 101 and 102:
Random Strategies 93 to write the n
Page 103 and 104:
Random Strategies 95 the expectatio
Page 105 and 106:
Random Strategies 97 maintained at
Page 107 and 108:
Random Strategies 99 works entirely
Page 109 and 110:
Random Strategies 101 the principle
Page 111 and 112:
Random Strategies 103 out, a limite
Page 113 and 114:
Chapter 5 Evolution Strategies for
Page 115 and 116:
The Two Membered Evolution Strategy
Page 117 and 118:
Page 119 and 120:
Page 121 and 122:
Page 123 and 124:
Page 125 and 126:
Page 127 and 128:
A Multimembered Evolution Strategy
Page 129 and 130:
Page 131 and 132:
Page 133 and 134:
Page 135 and 136:
Page 137 and 138:
Page 139 and 140:
Page 141 and 142:
Page 143 and 144:
Page 145 and 146:
Page 147 and 148:
Page 149 and 150:
Page 151 and 152:
Page 153 and 154:
Page 155 and 156:
Page 157 and 158:
Page 159 and 160:
Genetic Algorithms 151 too is the c
Page 161 and 162:
Genetic Algorithms 153 mean objecti
Page 163 and 164:
Genetic Algorithms 155 p( ∆x) 1 1
Page 165 and 166:
Genetic Algorithms 157 out any chan
Page 167 and 168:
Genetic Algorithms 159 Average Numb
Page 169 and 170:
Simulated Annealing 161 There are t
Page 171 and 172:
Tabu Search and Other Hybrid Concep
Page 173 and 174:
Chapter 6 Comparison of Direct Sear
Page 175 and 176:
Theoretical Results 167 Oettli, 196
Page 177 and 178:
Theoretical Results 169 where 0
Page 179 and 180:
Theoretical Results 171 tions. Simi
Page 181 and 182:
Numerical Comparison of Strategies
Page 183 and 184:
Page 185 and 186:
Page 187 and 188:
Page 189 and 190:
Page 191 and 192:
Page 193 and 194:
Page 195 and 196:
Page 197 and 198:
Page 199 and 200:
Page 201 and 202:
Page 203 and 204:
Page 205 and 206:
Page 207 and 208:
Page 209 and 210:
Page 211 and 212:
Page 213 and 214:
Page 215 and 216:
Page 217 and 218:
Page 219 and 220:
Page 221 and 222:
Page 223 and 224:
Page 225 and 226:
Page 227 and 228:
Page 229 and 230:
Page 231 and 232:
Page 233 and 234:
Page 235 and 236:
Page 237 and 238:
Page 239 and 240:
Page 241 and 242:
Core storage required 233 term \cor
Page 243 and 244:
Chapter 7 Summary and Outlook So, i
Page 245 and 246:
Summary and Outlook 237 numerical o
Page 247 and 248:
Summary and Outlook 239 considerabl
Page 249 and 250:
Summary and Outlook 241 is called t
Page 251 and 252:
Summary and Outlook 243 to the prod
Page 253 and 254:
Summary and Outlook 245 tition betw
Page 255 and 256:
Summary and Outlook 247 the experim
Page 257 and 258:
Chapter 8 References Glossary of ab
Page 259 and 260:
References 251 Anscombe, F.J. (1959
Page 261 and 262:
References 253 Bandler, J.W. (1969b
Page 263 and 264:
References 255 Bendin, F. (1992), E
Page 265 and 266:
References 257 Booth, A.D. (1955),
Page 267 and 268:
References 259 Brent, R.P. (1971),
Page 269 and 270:
References 261 Carroll, C.W. (1961)
Page 271 and 272:
References 263 Courant, R., D. Hilb
Page 273 and 274:
References 265 Davies, M., I.J. Whi
Page 275 and 276:
References 267 Dvoretzky, A. (1956)
Page 277 and 278:
References 269 Fiacco, A.V. (1974),
Page 279 and 280:
References 271 Fogel, L.J., A.J. Ow
Page 281 and 282:
References 273 Gill, P.E., W. Murra
Page 283 and 284:
References 275 Graves, R.L., P. Wol
Page 285 and 286:
References 277 Heckler, R., H.-P. S
Page 287 and 288:
References 279 Ho meister, F., H.-P
Page 289 and 290:
References 281 Idelsohn, J.M. (1964
Page 291 and 292:
References 283 Karnopp, D.C. (1966)
Page 293 and 294:
References 285 Kochen, M., H.M. Has
Page 295 and 296:
References 287 Kunzi, H.P., H.G. Tz
Page 297 and 298: References 289 LeCam, L.M., J. Neym
Page 299 and 300: References 291 Mamen, R., D.Q. Mayn
Page 301 and 302: 294 References Miele, A., H.Y. Huan
Page 303 and 304: 296 References Murray, W. (Ed.) (19
Page 305 and 306: 298 References Oldenburger, R. (Ed.
Page 307 and 308: 300 References Peschel, M. (1980),
Page 309 and 310: 302 References Powell, M.J.D. (1970
Page 311 and 312: 304 References Rechenberg, I. (1989
Page 313 and 314: 306 References Rybashov, M.V. (1969
Page 315 and 316: 308 References Schmidt, J.W., K. Ve
Page 317 and 318: 310 References Shedler, G.S. (1967)
Page 319 and 320: 312 References Steinbuch, K. (1971)
Page 321 and 322: 314 References Tabak, D. (1970), Ap
Page 323 and 324: 316 References Varela, F.J., P. Bou
Page 325 and 326: 318 References White, L.J., R.G. Da
Page 327 and 328: 320 References Youden, W.J., O. Kem
Page 329 and 330: 322 References Glossary of Abbrevia
Page 331 and 332: 324 References
Page 333 and 334: 326 Appendix A Problem 1.2 Objectiv
Page 335 and 336: 328 Appendix A Minimum: x =(3 0:5)
Page 337 and 338: 330 Appendix A Figure A.3: Graphica
Page 339 and 340: 332 Appendix A Several of the searc
Page 345 and 346: 338 Appendix A Minimum: Start: Prob
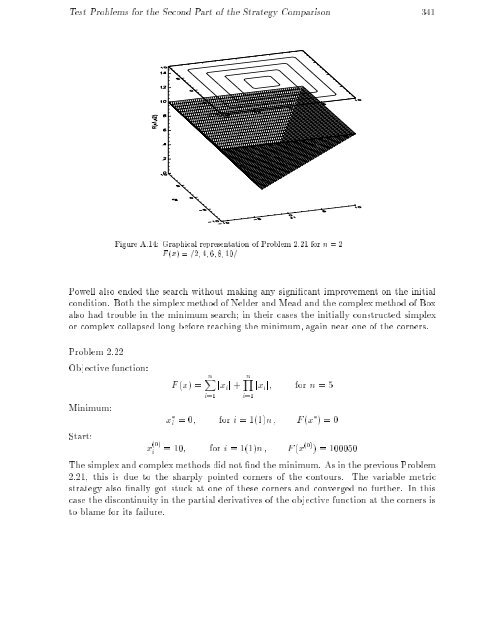
Page 347: 340 Appendix A Problem 2.20 Objecti
Page 351 and 352: 344 Appendix A Start: x (0) i =10 f
Page 353 and 354: 346 Appendix A on the interval 0 y
Page 355 and 356: 348 Appendix A Problem 2.32 after B
Page 357 and 358: 350 Appendix A Constraints: Gj(x) =
Page 359 and 360: 352 Appendix A The constraints form
Page 361 and 362: 354 Appendix A Start: x (0) =(250 2
Page 363 and 364: 356 Appendix A Problem 2.44 As Prob
Page 365 and 366: 358 Appendix A Figure A.29: Graphic
Page 367 and 368: 360 Appendix A Start: Figure A.31:
Page 369 and 370: 362 Appendix A Problem 3.2 (analogo
Page 371 and 372: 364 Appendix A Problem 3.6 (analogo
Page 373 and 374: 366 Appendix A Minimum: x i =0 for
Page 375 and 376: 368 Appendix B LF (integer) Return
Page 377 and 378: 370 Appendix B 4. Convergence crite
Page 379 and 380: 372 Appendix B 8. Function Z(S,R) T
Page 381 and 382: 374 Appendix B 25 L(K)=L(K+1) L(10)
Page 383 and 384: 376 Appendix B LF=2 (continued) No
Page 385 and 386: 378 Appendix B man), vol. 15 of Pro
Page 387 and 388: 380 Appendix B instead of T, as a p
Page 389 and 390: 382 Appendix B 15 CONTINUE 16 FF=F(
Page 391 and 392: 384 Appendix B SK(KS)=AMAX1(SM(I),A
Page 393 and 394: 386 Appendix B B.3 ( + ) Evolution
Page 395 and 396: 388 Appendix B EPSILO (one dimensio
Page 397 and 398: 390 Appendix B GLEICH (real functio
Page 399 and 400:
392 Appendix B GLEICH, and TKONTR d
Page 401 and 402:
394 Appendix B 1 NL=1+N-NS NM=N-1 N
Page 403 and 404:
396 Appendix B ZSTERN=ZBEST K=LBEST
Page 405 and 406:
398 Appendix B C NEGATIVE (LETHAL M
Page 407 and 408:
400 Appendix B C C PREPARE FINAL DA
Page 409 and 410:
402 Appendix B 2 IF(.NOT.BKOMMA.OR.
Page 411 and 412:
404 Appendix B 32 WRITE(KANAL,126)
Page 413 and 414:
406 Appendix B DO 4 I=1,NX KI=KI1 I
Page 415 and 416:
408 Appendix B Subroutine MINMAX MI
Page 417 and 418:
410 Appendix B 2 IF(U.LT..965487131
Page 419 and 420:
412 Appendix B parameters by multip
Page 421 and 422:
414 Appendix B
Page 423 and 424:
416 Appendix C - SIMP Simplex strat
Page 425 and 426:
418 Appendix C C.3.2 How to Install
Page 427 and 428:
420 Appendix C { } return(0.26*(x[0
Page 429 and 430:
422 Appendix C 1 No recombination 2
Page 431 and 432:
424 Appendix C 8e-07 8e-07 Initial
Page 433 and 434:
426 Index Banach, S., 10 Bandler, J
Page 435 and 436:
428 Index Coordinate strategy, 41{4
Page 437 and 438:
430 Index Evolution strategy, 3, 6,
Page 439 and 440:
432 Index Graves, R.L., 23 Great de
Page 441 and 442:
434 Index Khurgin, Ya.I., 89 Kiefer
Page 443 and 444:
436 Index Michie, D., 102 Mickey, M
Page 445 and 446:
438 Index Parkinson, J.M., 61 Parta
Page 447 and 448:
440 Index Rotating coordinates meth
Page 449 and 450:
442 Index Storey, C., 23, 50, 54 St
Page 451:
444 Index Wilson, S.W., 103 Witt, U
show all

Evolution and Optimum Seeking

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?