link to my thesis

56 CHAPTER 5. ND-SYSTEMS APPROACH IN POLYNOMIAL OPTIMIZATION
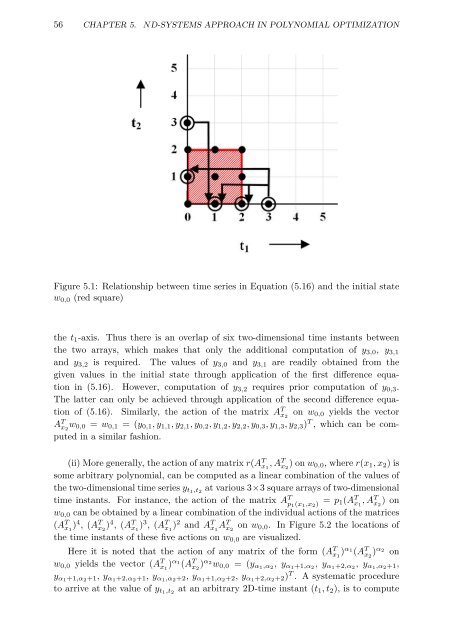
Figure 5.1: Relationship between time series in Equation (5.16) and the initial state
w 0,0 (red square)
the t 1 -axis. Thus there is an overlap of six two-dimensional time instants between
the two arrays, which makes that only the additional computation of y 3,0 , y 3,1
and y 3,2 is required. The values of y 3,0 and y 3,1 are readily obtained from the
given values in the initial state through application of the first difference equation
in (5.16). However, computation of y 3,2 requires prior computation of y 0,3 .
The latter can only be achieved through application of the second difference equation
of (5.16). Similarly, the action of the matrix A T x 2
on w 0,0 yields the vector
A T x 2
w 0,0 = w 0,1 =(y 0,1 ,y 1,1 ,y 2,1 ,y 0,2 ,y 1,2 ,y 2,2 ,y 0,3 ,y 1,3 ,y 2,3 ) T , which can be computed
in a similar fashion.
(ii) More generally, the action of any matrix r(A T x 1
,A T x 2
)onw 0,0 , where r(x 1 ,x 2 )is
some arbitrary polynomial, can be computed as a linear combination of the values of
the two-dimensional time series y t1,t 2
at various 3×3 square arrays of two-dimensional
time instants. For instance, the action of the matrix A T p = p 1(x 1,x 2) 1(A T x 1
,A T x 2
)on
w 0,0 can be obtained by a linear combination of the individual actions of the matrices
(A T x 1
) 4 ,(A T x 2
) 4 ,(A T x 1
) 3 ,(A T x 1
) 2 and A T x 1
A T x 2
on w 0,0 . In Figure 5.2 the locations of
the time instants of these five actions on w 0,0 are visualized.
Here it is noted that the action of any matrix of the form (A T x 1
) α1 (A T x 2
) α2 on
w 0,0 yields the vector (A T x 1
) α1 (A T x 2
) α2 w 0,0 = (y α1,α 2
,y α1+1,α 2
,y α1+2,α 2
,y α1,α 2+1,
y α1+1,α 2+1, y α1+2,α 2+1, y α1,α 2+2, y α1+1,α 2+2, y α1+2,α 2+2) T . A systematic procedure
to arrive at the value of y t1,t 2
at an arbitrary 2D-time instant (t 1 ,t 2 ), is to compute