Komplexitaet-WS-2010.. - Parallele Systeme

Komplexitätstheorie - Wintersemester 2010/2011 91
u1[1]
u1[1] u1[2]
7
1
2
u1[2]
s1,s2[1]
u2[2]
u2[1]
u2[1] u2[2]
8
3 4
s1,s2[2]
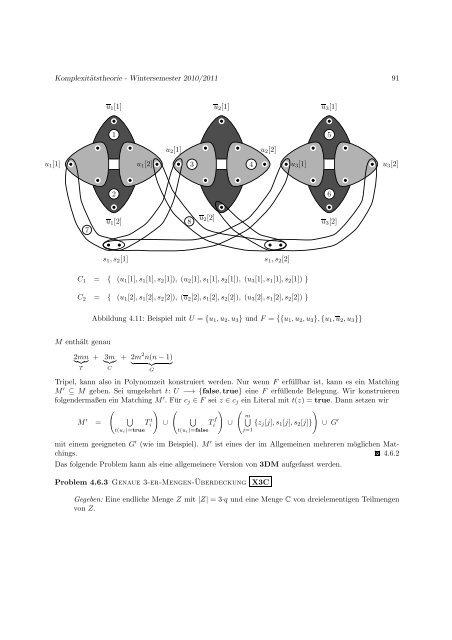
C1 = { (u1[1],s1[1],s2[1]), (u2[1],s1[1],s2[1]), (u3[1],s1[1],s2[1]) }
C2 = { (u1[2],s1[2],s2[2]), (u2[2],s1[2],s2[2]), (u3[2],s1[2],s2[2]) }
M enthält genau
2mn
T
u3[1]
5
u3[1] u3[2]
6
u3[2]
Abbildung 4.11: Beispiel mit U = {u1,u2,u3} und F = {{u1,u2,u3},{u1,u2,u3}}
+ 3m
C
+ 2m 2 n(n−1)
G
Tripel, kann also in Polynomzeit konstruiert werden. Nur wenn F erfüllbar ist, kann es ein Matching
M ′ ⊆ M geben. Sei umgekehrt t: U −→ {false,true} eine F erfüllende Belegung. Wir konstruieren
folgendermaßen ein Matching M ′ . Für cj ∈ F sei z ∈ cj ein Literal mit t(z) = true. Dann setzen wir
M ′ =
∪
m
∪ {zj[j],s1[j],s2[j]} ∪ G
j=1
′
T
t(ui)=true
t
i
T
t(ui)=false
f
i
mit einem geeigneten G ′ (wie im Beispiel). M ′ ist eines der im Allgemeinen mehreren möglichen Matchings.
4.6.2
Das folgende Problem kann als eine allgemeinere Version von 3DM aufgefasst werden.
Problem 4.6.3 Genaue 3-er-Mengen-Überdeckung X3C
Gegeben: Eine endliche Menge Z mit |Z| = 3·q und eine Menge C von dreielementigen Teilmengen
von Z.