- Page 1 and 2:
McGRAW-I4ILL SERIES IN MECHANICAL E
- Page 3 and 4:
vi Contents CIIAPTEII V. Exnct ~olu
- Page 5:
Y Contents A " I XI X 'I'lirorrt.ir
- Page 8 and 9:
xvi I'orcworcI Thc result was t.11~
- Page 10 and 11:
From Author's Preface to the First
- Page 12 and 13:
the aid of thorctical considcmtioti
- Page 14 and 15:
even in fluitls wit,lt vcry srnall
- Page 16 and 17:
10 I. Or~llinr of lluicl rnot,ion w
- Page 18 and 19:
The vclwil y IL at some point i11 t
- Page 20 and 21:
Fig. 1.6. Firld of flow of oil nho~
- Page 22 and 23:
22 I. Outliric of fluid motion with
- Page 24 and 25:
2 (i TI. O~~tlittr of Imun~lnry-lsy
- Page 26 and 27:
Fie. 2.511 Fig. 2 .5~ Fig. 2.5b Fig
- Page 28 and 29: S - point orscpnrnt.ion T'ig. 2.12.
- Page 30 and 31: 3 8 \ Y?\ If. 011tli11e of boundary
- Page 32 and 33: 42 11. 011tli11e of Iw~~ntlnry-Inyr
- Page 34 and 35: [:j2a] I?o~cilhrntl, I,.: Thr forn~
- Page 36 and 37: 50 111. l)crivnt,ion of thc cquntio
- Page 38 and 39: Fig. 3.3. Tmcd clintor1,ion of flui
- Page 40 and 41: of flltitl is strcsscd in thrcc nlu
- Page 42 and 43: 1:i~ 3.8. Qltnsintzt.ia cotnprrssio
- Page 44 and 45: 66 111. 1)wivntion of the eqnntions
- Page 46 and 47: CHAPTER I V General properties of t
- Page 48 and 49: 74 TV. Gencrol proprtic~ of tho Nov
- Page 50 and 51: Ilcre v, c, :tntl k tlrnol,c 1.I1t:
- Page 52 and 53: conclil.ion (4.14) plays n part wl~
- Page 54 and 55: 86 V. 1':xact solul ions of tlir N:
- Page 56 and 57: 90 V. ICxnct sol~ttion~ of tho Nnvi
- Page 58 and 59: 94 V. Exnct sohltiono ol' tho Nnvic
- Page 60 and 61: Table 5.1. Functions occrtrring in
- Page 62 and 63: 11. Flow taenr n rotnting disk. A f
- Page 64 and 65: 106 V. JCxact solutions of the Navi
- Page 66 and 67: cnu bo npplirtl nt mont, nn fnr RS
- Page 68 and 69: 114 VI. Vcry slow motion where r2 =
- Page 70 and 71: 1 I8 VT. Very slow motion r. 'l'l~o
- Page 72 and 73: 122 VI. Very rrlow motion ext.endcd
- Page 74 and 75: 126 VT. \'cry slow rnot.ion Part B.
- Page 76 and 77: 130 VII. Boundnry-layor cquntionzl
- Page 80 and 81: 138 VII. no~~ndnry-layer cqnntions
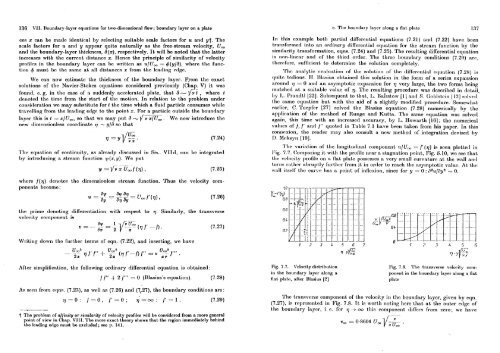
- Page 82 and 83: 142 VII. Hor~nclnry-lnyrr rq~~ntii~
- Page 84 and 85: 146 VII. I~o~~ntlnr~ Inyrr cq~~ntio
- Page 86 and 87: CIIAFTER VIII Gencral propertiee of
- Page 88 and 89: 164 VIII. Ccnernl propertic8 of Lhe
- Page 90 and 91: 158 VIII. General ppropcrtics of th
- Page 92 and 93: VIII. General propertien of the bou
- Page 94 and 95: 'I'his c.quat,ion Lmnsforms into t1
- Page 96 and 97: 170 TX. 1Sxact uolutions of t.ho st
- Page 98 and 99: 174 TX. Exnct ~olut,ionu of tho sto
- Page 100 and 101: 178 IX, Exact solutions of tlrc ste
- Page 102 and 103: and t,llc? clnsh now clet~otos tlil
- Page 104 and 105: 1 86 10 0.8 0.6 0.4 0.2 0 -0.2 -0.4
- Page 106 and 107: ccnt,rred nt, (m -1- 1, n). 1'110 t
- Page 108 and 109: 194 IX. Jqxnct eolutions of thc stc
- Page 110 and 111: O~l:cr ehnpw: Second-order cITcetls
- Page 112 and 113: 202 X. Approximate rncl.hoda for st
- Page 114 and 115: 206 X. Approxitnnte rnct.l~otls for
- Page 116 and 117: 210 X. Approximate mcthod~ for shad
- Page 118 and 119: 214 X. Approximato mothotls for sha
- Page 120 and 121: 218 X. Approximntn met,hods for shn
- Page 122 and 123: 222 X. Approximate methods for stea
- Page 124 and 125: 220 XI. Axinlly symniobricnl nnd th
- Page 126 and 127: 230 XI. Axinlly symmctricnl and thr
- Page 128 and 129:
23.1- XI. Axially uynimet.rira1 nnc
- Page 130 and 131:
the two wries expnnsicws for sin (%
- Page 132 and 133:
242 XI. Axially nymmct.riral and tl
- Page 134 and 135:
in cross-flow, tlrprntls only on lh
- Page 136 and 137:
250 XI. Axinlly nyrnmet,rirnl nntl
- Page 138 and 139:
XI. Axinlly ~,vn~n~et.rir;~l nnrl I
- Page 140 and 141:
258 XI. AxhIly syn~rnrtrirnl nncl t
- Page 142 and 143:
. . lit 1 h1:lgt.r. '1.: 'l'l~idc I
- Page 144 and 145:
206 XIT. l'l~rr~nnl bo1111r11iry ln
- Page 146 and 147:
270 XIT. 'I'l~rrtnal boundary layer
- Page 148 and 149:
can I)r rct.ni~rrvl in inrotnl~rrss
- Page 150 and 151:
if wc: pillf - - 'I1, - (A7'),. 11,
- Page 152 and 153:
Rotntirig rli~k: (:II:I~I. V, in pn
- Page 154 and 155:
286 X11. 'IY~rrrr~al bo~~ndnry laye
- Page 156 and 157:
290 XlI. Tl~rrnmal boundary layers
- Page 158 and 159:
with 0,' -. () at, r] - 0 and 0, =
- Page 160 and 161:
2!)H XI[. Thcrn~al bor~nrlnry Inyrr
- Page 162 and 163:
302 XJI. Therninl boundary layers i
- Page 164 and 165:
306 XII. Tllcrrnal hor~ndary layers
- Page 166 and 167:
310 XJI. 'I'hcrmnl boundnry layers
- Page 168 and 169:
314 X11. Thermal boundary laycrs in
- Page 170 and 171:
318 XIT. Tl~crnial bonndnry layers
- Page 172 and 173:
322 XII. Tl~or~nnl I)onndnry lnyers
- Page 174 and 175:
326 X l I. 'l'l~crn~nl hounrlnry ln
- Page 176 and 177:
330 X[[1. lmninar bor~ndnry lnyers
- Page 178 and 179:
334 XIIT. Lnrninnr 1)oundary laycra
- Page 180 and 181:
338 XI I I. Im~linnr I>orirtclt~ry
- Page 182 and 183:
342 XI11. Tmninnr Imlndary layeru i
- Page 184 and 185:
346 XI 11. T,ntninar I~or~nrjary hy
- Page 186 and 187:
350 XIII. 1,mninnr honnclxry lnycrn
- Page 188 and 189:
354 XI 11. 1,nminnr h~nrlnry 1:ryrm
- Page 190 and 191:
Fig.. l3.16. In 13.18. lain~innr ho
- Page 192 and 193:
a Intninn.r l)out~rlary I:~.ycr, bu
- Page 194 and 195:
1 I Itc vnriolts c4Twl.s ol'sl~oclt
- Page 196 and 197:
370 XIIJ. I~tminar boundary layers
- Page 198 and 199:
\'all I)rirst., 15.11..: 'l'hr prol
- Page 200 and 201:
CIIAPTER XIV Boundary-layer control
- Page 202 and 203:
5. J'rrvrntion of trauaitinn by the
- Page 204 and 205:
frorii th; 1c;ulitig rxlge! (l3l:wi
- Page 206 and 207:
390 XIV. Ilo~~n~lnry-lnycr contml F
- Page 208 and 209:
. - v, (x) =cons/ Fig. 14.14. 1,ant
- Page 210 and 211:
invc?st.igai.ctl. In this msc too,
- Page 212 and 213:
402 XIV. Dounclery-layer control 1.
- Page 214 and 215:
Ni\('A 'rM !I74 (1!)41). 1861 Sinli
- Page 216 and 217:
110 XV. Non-~teldy bortndnry layers
- Page 218 and 219:
414 XV. Non-st.cncly hour~tlnry Iny
- Page 220 and 221:
418 XV. Non-slmrly l~orrnclnry Inyr
- Page 222 and 223:
422 XV. Non-st,cndy hoixnd~ry Inycr
- Page 224 and 225:
420 XV. Non-nl,mdy Fig. 15.58 Fig.
- Page 226 and 227:
XV. Non-utcncly boouclary lnyers wh
- Page 228 and 229:
434 XV. Non-stcxcly boundary layers
- Page 230 and 231:
438 XV. Non-atcndy boundnry inyer~
- Page 232 and 233:
442 XV. Norl-st,aady boundary Isycr
- Page 234 and 235:
440 XV. Non-st,rndy ho~~nclnry laye
- Page 236 and 237:
450 XVI. Origin of tnrhulence I pyi
- Page 238 and 239:
XVT. Origin of turbulcncc I n. Some
- Page 240 and 241:
458 XVI. Origin of turbulence I b.
- Page 242 and 243:
462 XVI. Origin of tnrb~rlmcc 1 num
- Page 244 and 245:
466 XVi. Origin of t.r~rhr~lrncc 1
- Page 246 and 247:
470 XVI. Origin of h~rlwlcnce T I R
- Page 248 and 249:
474 XVI. Origin of l,t~rl~~tlct~rr
- Page 250 and 251:
478 XVI. Origin of I.rtrb~tlmcr 1 t
- Page 252 and 253:
482 XVT. Origin of tmbulcncc I c. E
- Page 254 and 255:
486 XVI. Origin of k~rbulenre I 148
- Page 256 and 257:
490 XVII. Origin ol t,urbulencc 11
- Page 258 and 259:
404 XVII. Oriein of tnrbnlencc TI F
- Page 260 and 261:
498 XVII. Origin of turbnlmco II t,
- Page 262 and 263:
Tlw tlisl.nr~cc Iwt,wccn the point,
- Page 264 and 265:
c. Efict of ~urtintl on trnt~nition
- Page 266 and 267:
510 XVl I. Origin of Idmlrnro I I '
- Page 268 and 269:
514 , XVII. Origin of turbulence 11
- Page 270 and 271:
518 XVI I. Origin of turhr~lcncc 11
- Page 272 and 273:
on the bnsis of t.hc tl~corct,ical
- Page 274 and 275:
626 XVII. Origin oI t.11r011lonco I
- Page 276 and 277:
630 XVII. Origin ot t.~~rhr~lrncc J
- Page 278 and 279:
XVII. Origin of t.urh~~lencc TI 7 !
- Page 280 and 281:
638 XVII. Origin of t~~~rbnlc~~rr I
- Page 282 and 283:
\vi(,l~ a (-ylit~(lw envcrv(1 wiI.1
- Page 284 and 285:
646 XVII. Origin of turbulence TI F
- Page 286 and 287:
550 X\'ll. Origin of t,11rh111rnrc
- Page 288 and 289:
554 XVII. Origin of t,rlrbuloncc TI
- Page 290 and 291:
558 XVITI. Fundamentals of tr~rbule
- Page 292 and 293:
562 XVlI1. R~nclnmont.nIu of tur1)u
- Page 294 and 295:
The corrrlnt,ion co~ffiricnt~ y~ ra
- Page 296 and 297:
670 XV111. I'nntlntnrt~t~nlrr of tt
- Page 298 and 299:
574 XVIII. 1'undnnient.alu of tnrl~
- Page 300 and 301:
CHAPTER XIX Theoretical assumptions
- Page 302 and 303:
682 XIX. Thcoroticnl wsltmptionu fo
- Page 304 and 305:
586 XIX. Throretical aaotin~ptiona
- Page 306 and 307:
5l)O XIX. Tl~rorrt,icnl nmumptions
- Page 308 and 309:
594 XIX. 'rheoreticnl nssornptions
- Page 310 and 311:
698 XX. 'I'~~rl~ulrnt flow f,lrro~~
- Page 312 and 313:
602 XX. T~rrbulcnt flow thro~tgh pi
- Page 314 and 315:
606 XX. 'l't~rhl~lc~rit flow thro~~
- Page 316:
GI0 XX. Turbulent flow throngh pip
- Page 319 and 320:
Icror~~ ()I(, phj.sic*:~l ~)oint. o
- Page 321 and 322:
620 XX. Tnrbnlcnt flow tlvough pipe
- Page 323 and 324:
dimensions Fig. 20.26. 1tc.sist.anc
- Page 325 and 326:
628 XX. T~lrbnlmt flow through pipe
- Page 327 and 328:
632 XX. Turhulcnt flow through pipc
- Page 329 and 330:
636 XXI. Td~nlcnt houndnry layers a
- Page 331 and 332:
610 XXI. Ttrrbulent bor~ndnry layer
- Page 333 and 334:
644 XXI. Turbulent boundary laycrs
- Page 335 and 336:
048 XXI. Turbulent boundary layers
- Page 337 and 338:
652 XXI. Turt)~~lcnt houndnry layer
- Page 339 and 340:
656 XXI. Turbulent boundnry layers
- Page 341 and 342:
660 XX I. Tl~rhlent bo~~ndary layer
- Page 343 and 344:
664 XXI. Turbulent boundary layers
- Page 345 and 346:
CHAPTER XXII The incompreesible tur
- Page 347 and 348:
672 XXll. 'l'llc incon~prcssiblc tu
- Page 349 and 350:
070 XXII. Tlic incompreaaibto lnrl)
- Page 351 and 352:
FRO XXII. Tho incornprcs~iblo turbu
- Page 353 and 354:
684 XXII. 'Yhc incon~prcssible Lnrb
- Page 355 and 356:
688 XXJI. The incon~prcssible t,urb
- Page 357 and 358:
002 XXI1. Tho inro~nprc~sil~lo tt~r
- Page 359 and 360:
is prol)nt~t,iot~nl to the rnclius.
- Page 361 and 362:
lf$8] Mucsm:tnn, 11.: Z~~snrntncnhn
- Page 363 and 364:
70-t XX I1 I. 'Ihrbulcnt bonrwlnry
- Page 365 and 366:
708 XXIII. Turbulent bonndnry Iaycr
- Page 367 and 368:
712 XXI 11. 'I'~~rl~~~lemt bo~~ntln
- Page 369 and 370:
716 XXIII. 'I'urbr~lcnt bor~ntlnry
- Page 371 and 372:
720 XXIII. Turbulent boundary layer
- Page 373 and 374:
724 XXlll. 'rur1)ulcnt boundnry Iny
- Page 375 and 376:
[04] Smith, P.D.: An integral predi
- Page 377 and 378:
732 XXIV. Frcc trtrbt~lent flows; j
- Page 379 and 380:
700 XXIV. Prrc tr~rb~tlent flowa; j
- Page 381 and 382:
Neglecting u12, we obtain XXIV. Prc
- Page 383 and 384:
744 XXIV. lhc L~trl)ulcnt Ilow~; jo
- Page 385 and 386:
748 XXIV. Free turbulent flowa; jet
- Page 387 and 388:
762 XXIV. Frcc td)ulcnt flows; jcta
- Page 389 and 390:
756 XXIV. Prrc torbulent flows; jet
- Page 391 and 392:
760 XXV. DotcrminnLion of profilo d
- Page 393 and 394:
764 XXV. I)ot.crtninntiotl of profi
- Page 395 and 396:
768 XXV. Determination of profile d
- Page 397 and 398:
XXV. 1)obrlninalion of proRlo drag
- Page 399 and 400:
776 XXV. 1)ctormination of profile
- Page 401 and 402:
A. Reviews organized in serial publ
- Page 403 and 404:
784 Bibliography Sherman, I?. S., I
- Page 405 and 406:
Clementa, lt.R., and Mad, D.J.: The
- Page 407 and 408:
792 Bihliography 13ird, R.R., Slewn
- Page 409 and 410:
Oswatitach, I
- Page 411 and 412:
H:I:IR, 11. 776, 777 Ilnnsr. 1). 62
- Page 413 and 414:
Scl~crb:trl,l~, I
- Page 415 and 416:
805 811bjrct lntlrx 209, 354, 385,
- Page 417 and 418:
812 Snhjcct lntlcx - vorl.irrs 526,
- Page 419:
List of most commonly used synibola