Michael Corral: Vector Calculus

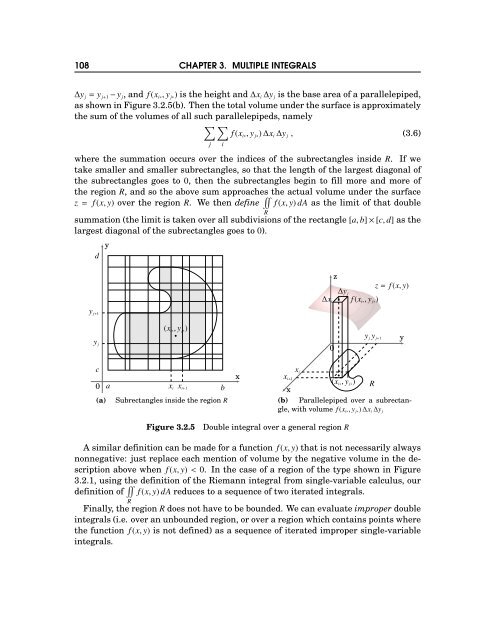
108 CHAPTER 3. MULTIPLE INTEGRALS
∆y j = y j+1 −y j , and f(x i∗ ,y j∗ ) is the height and∆x i ∆y j is the base area of a parallelepiped,
asshowninFigure3.2.5(b). Thenthetotalvolumeunderthesurfaceisapproximately
the sum of the volumes of all such parallelepipeds, namely
∑∑
f(x i∗ ,y j∗ )∆x i ∆y j , (3.6)
j
i
where the summation occurs over the indices of the subrectangles inside R. If we
take smaller and smaller subrectangles, so that the length of the largest diagonal of
the subrectangles goes to 0, then the subrectangles begin to fill more and more of
the region R, and so the above sum approaches the actual volume under the surface
z= f(x,y) over the region R. We then define f(x,y)dA as the limit of that double
R
summation (the limit is taken over all subdivisions of the rectangle [a,b]×[c,d] as the
largest diagonal of the subrectangles goes to 0).
d
y
z
z= f(x,y)
∆y j
f(x i∗ ,y j∗ )
∆x i
(x i∗ ,y j∗ )
y j+1
(x i∗ ,y j∗ )
y j
c
0 a x i x i+1 b
(a) Subrectangles inside the region R
x
y j y j+1 y
0
x i
x i+1
R
x
(b) Parallelepiped over a subrectangle,
with volume f(x i∗ ,y j∗ )∆x i ∆y j
Figure 3.2.5 Double integral over a general region R
A similar definition can be made for a function f(x,y) that is not necessarily always
nonnegative: just replace each mention of volume by the negative volume in the description
above when f(x,y)