Lectures on String Theory
Lectures on String Theory
Lectures on String Theory
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
– 90 –<br />
gluing the opposite sides to the can<strong>on</strong>ical form depicted <strong>on</strong> Fig.9, which corresp<strong>on</strong>ds<br />
to Imτ > 0.<br />
z<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
¡¡¡¡¡<br />
¢¡¢¡¢¡¢¡¢¡¢¡¢<br />
¡<br />
Fig. 8. Defining the torus by factorizing the complex z-plane.<br />
The parameter τ takes values in the upper half-plane which is called Teichmüller<br />
space. The parameter τ itself is named the modular or Teichmüller parameter. The<br />
Teichmüller parameter is not yet a parameter describing the moduli space.<br />
+1<br />
0<br />
1<br />
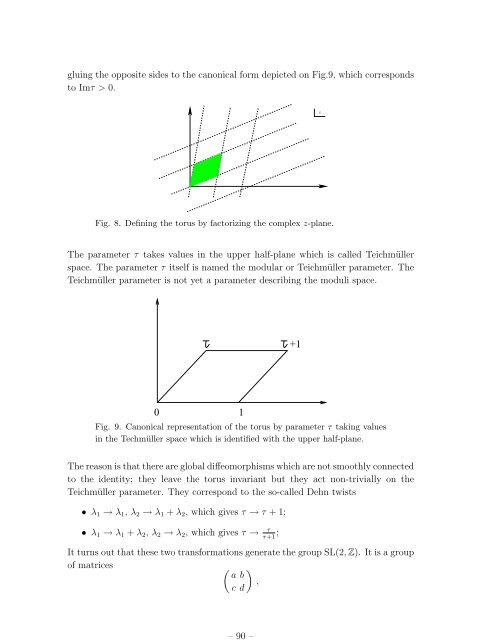
Fig. 9. Can<strong>on</strong>ical representati<strong>on</strong> of the torus by parameter τ taking values<br />
in the Techmüller space which is identified with the upper half-plane.<br />
The reas<strong>on</strong> is that there are global diffeomorphisms which are not smoothly c<strong>on</strong>nected<br />
to the identity; they leave the torus invariant but they act n<strong>on</strong>-trivially <strong>on</strong> the<br />
Teichmüller parameter. They corresp<strong>on</strong>d to the so-called Dehn twists<br />
• λ 1 → λ 1 , λ 2 → λ 1 + λ 2 , which gives τ → τ + 1;<br />
• λ 1 → λ 1 + λ 2 , λ 2 → λ 2 , which gives τ →<br />
τ ; τ+1<br />
It turns out that these two transformati<strong>on</strong>s generate the group SL(2, Z). It is a group<br />
of matrices<br />
( ) a b<br />
,<br />
c d