Volume 61 Issue 2 (2011) - Годишник на ТУ - София - Технически ...

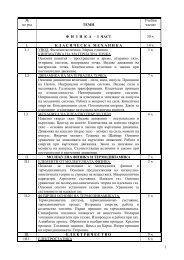
∣∣E (k)C n∣ ∣∣ =Proposition 3.4 For any k ∈ C n the order of the semiring E (k)C nis( ) ( )2k 2n − 2k − 2.k n − k − 1Proof. Let us consider the arbitrary endomorphismf = ≀ i 0 , . . . , i k−1 , k, i k+1 , . . . , i n−1 ≀ of the semiring E (k)C nand let (i 0 , i 1 . . . , i k ), wherei k = k is the ordered k + 1 – tuple corresponding to the first part of f. Insteadof the any k + 1 – tuple (i 0 , . . . , i k ) we consider the corresponding k + 1 – tuple(k − i k , . . . , k − i 0 ) = (0, . . . , k − i 0 ). These k + 1 – tuples satisfy the conditions ofProposition 3.7 of [6], so their number is( 2kk).Let us consider the last part (k, i k+1 , . . . , i n−1 ) of the endomorphism f. For suchn − k – tuple we compare the n − k – tuple (0, i k+1 − k, . . .(, i n−1 − k). The ) number2n − 2k − 2of the last n − k – tuples from Proposition 3.7 of [6] is. So the( )( n − k − 1 )2k 2n − 2k − 2number of all endomorphisms f such that f(k) = k is.k n − k − 1∣ ( )∣Remark 3.5 For k = 0 from Proposition 3.4 follows that ∣E (0) ∣∣ 2n − 2C n=n − 1which is the result of Proposition 3.7 of [6]. For k = n−1 we have the same number∣ ( )∣∣E (n−1) ∣∣ 2n − 2C n= .n − 1Proposition ) 3.6 For any k ∈ C n follows that:a. CO(ÊCn ∩ E (k)C n= {≀ k k . . . k ≀}.b. The endomorphism ≀ k k . . . k ≀ is a multiplicative absorbing element of thesemiring E (k)C n.Proof. a. For m ≠ k the endomorphism ≀ m m . . . m ≀ doesn’t belong to E (k)C n.b. The reasonings are similar to that of the proof of Proposition 3.1.Proposition 3.7 a. For k = 0 and k = n − 1 there is a subsemiring R of ÊC nsuch that E (k)C n∩ R = ∅ and ÊC n= E (k)C n∪ R.b. For k = {1, 2, . . . , n − 1} a subsemiring R of ÊC nsuch that E (k)C n∪ R doesn’t exists.Ê Cn = E (k)C n∩ R = ∅ andProof. a. For)k = 0 in the proof of part (iii) ) of Proposition 2.2 we shaw thatE (0)C n∩ A (1)(ÊCn 0 = ∅ and ÊC n= E (0)C n∪ A (1)(ÊCn 0 . From Proposition 2.4 (i) follows) (ÊCnthat A (1)0 is a subsemiring of ÊC n.For k = n − 1 set of the endomorphisms f such that f(n − 1) ≠ n − 1 is justthe semiring B (n−2)n−1Ê Cn = E (n−1)C n∪ B (n−2)n−1) (ÊCn – Proposition 2.5 (i). So, E (n−1)C)n(ÊCn .∩ B (n−2)n−1) (ÊCn = ∅ and16