Einführung in die Psychologie, Farbwahrnehmung - am Institut für ...

hat, denn singuläre Matrizen sind nicht
invertierbar.
Matrixinversion erfordert viel umständliche
Rechnung. Deshalb benutzt man
heute dazu ein Expertensystem, wie Maple
oder Mathematica. Ein Maple-Skript wird
in der Virtuellen Universität Regensburg
beigegeben. Es ist von praktischer Bedeutung,
da ein Wechsel der Primärfarben
nicht selten ansteht, etwa bei einem Beleuchtungswechsel
oder beim Übergang
von einer Farbfernsehbildröhre zu einer
anderen mit unterschiedlichen Phosphoren.
Helmholtz’ Dimensionsthatsache
Die Anzahl der Dimensionen des Farbraumes
wird durch die Angabe m variabel
gehalten. Das liegt daran, daß nur für
Normalsichtige m = 3 gilt. Farben blinde,
über die noch später zu berichten sein
wird, besitzen meistens ein m =2. Welche
Dimensionszahl vorliegt ist theoretisch (in
der Graßmannstruktur) durch die lineare
Abhängigkeit bzw. Unabhängigkeit der
Farbkoordinaten, also der Dosierungen der
Primärfarben zur Mischung einer vorgegebenen
Farbe bestimmt. Die größte Anzahl
linear unabhängiger Farbkoordinaten (eindeutiger
Dosierungen) bestimmt die Dimensions-zahl
m. Deshalb ist der folgende
Satz beweisbar:
Satz 3: Der Vektorraum ist m-dimensional,
g.d.w. < A , , *,~> m-chromatisch ist.
Die Beweise
Die Beweise für die drei Sätzt findet man
bei Krantz (1975). Dieser Autor hat die
Entdeckungen von Graßmann (1853) präzisiert
und, wo nötig ergänzt. Der Beweisgedanke
ist grundsätzlich der gleiche wie
bei der mathematischen Rechtfertigung des
Fingerrechnens. Eine Halbgruppe, hier die
Halbgruppe der Spektren zusammen mit
der Operation der Farbmischung, läßt sich
in eine Gruppe einbetten, weil sie die dafür
erforderlichen zusätzlichen Eigenschaften
besitzt, nämlich die Aufhebungseigenschaften.
Das Gedankengebäude betrifft
die Psychologie, weil sich die beiden Aufhebungseigenschaften
als Graßmannsche
Gesetze im Wahrnehmungslabor experimentell
realisieren lassen. Die Details der
Beweise übersteigen den Stoff dieser Darstellung.
Der Vektorraum der Farben
Wenn nun durch die Repräsentation eine
analytische Geometrie zur Verfügung
steht, läßt sich diese auch anschaulich, man
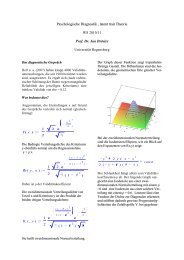
sagt synthetisch, nutzen. In der Abbildung
sieht man den Teilraum C, auf den sich die
Repräsentation bezieht, als Tütenförmigen
Bereich. Ein Primärfarbentripel ist durch
die Vektoren R,G,B hervorgehoben.
Abb.: Der konvexe Kegel der Farben im
Farbraum. Eingezeichent die Ebene (1, 1,
1).
In dem abgebildeten Falle durchstoßen die
Primärvalenzen den Rand des tütenförmigen
konvexen Kegels. Das macht den Bereich
der Farben, die aus diesem Tripel in
eigentlicher Mischung herstellbar sind,
besonders groß. Grundsätzlich können aber
die Primärvalenzen beliebig in den Kegel
gelegt werden, solange sie nicht alle drei in
einer einzigen Ebene zu liegen kommen.
Dann wäre stets eine der vorgesehen Primärvalenzen
aus den beiden anderen ermischbar,
und sie würden deshalb keinen
dreidimensionalen Farbraum aufspannen.