Querschnitt 21 / Februar 2007 - h_da: Hochschule Darmstadt

Querschnitt 21
Dar(p)-prozess
Sei X n das nte Symbol in einer durch einen DAr(p)-Prozess
generierten Sequenz. Dann ist X n gegeben durch die folgende
rekursive Anweisung (Jacobs und Lewis, 1978; Dehnert et al.,
2003):
X n = V n X n-An + (1 – V n ) Y n , n = p + 1, p + 2, … . (1)
Der erste Term in diesem rekursiven Modell ist für die Markov-eigenschaft
verantwortlich, während der zweite Term unkorrelierte,
zufällig gezogene Symbole aus dem Alphabet in
die Sequenz einfließen lässt. Die Zufallsvariable V n nimmt die
Werte 0 und 1 an und wirkt damit als Schalter zwischen den
zwei Termen der rechten Seite von Gleichung (1). Der Wert V n =
1 tritt mit der Wahrscheinlichkeit ρ ein, der Wert V n = 0 mit der
verbleibenden Wahrscheinlichkeit 1–ρ. Die weiteren Parameter
dieses Prozesses verbergen sich in der Zufallsvariablen A n .
Diese nimmt die Werte 1, 2, …, p an, und zwar mit den Wahrscheinlichkeiten
α 1 , α 2 , …. , α p . Die Werte α k regulieren dabei, wie
oft das Symbol X n in der Sequenz durch das Symbol X n-k , das
k Schritte in der Sequenz zurückliegt, determiniert wird, falls
ein Rückgriff erfolgt. Als letzten Baustein besitzt der Prozess die
11
zufällige Symbole
Markov-Ordnung p
…TAGCTTC…AGA
. . .
α p
α 3
C T
A
G A
G C
T
α 2
α 1
zufälliges Symbol
(Wahrscheinlichkeit 1-ρ)
historisches Symbol
(Wahrscheinlichkeit ρ)
Abbildung 1 • Schematische Darstellung des DAr(p)-Prozesses aus Gleichung (1). ein neues Symbol der Sequenz wird entweder durch Ziehen eines zufälligen Symbols
oder durch rückgriff auf ein Vorgängersymbol bestimmt. Die maximale rückgriffweite ist durch die festgelegte Markov-Ordnung p gegeben. (Angepasst aus:
Hütt und Dehnert, 2006.)
Zufallsvariable Y n , die Werte des Alphabets nach einer festzulegenden
Verteilung π, der Marginalverteilung, annimmt. Die
Zufallsvariablen V n , A n und Y n werden als unabhängig angesehen.
Die Sequenz X n hat eine Markov-eigenschaft pter Ordnung,
wobei die Werte α k per Konstruktion die Stärke der Korrelation
im Abstand k beschreiben. ein großer Vorteil dieses Korrelationsmaßes
gegenüber anderen (z. B. der Transinformation)
ist, dass der Schätzprozess mit dem Parameter ρ explizit die
Menge an zufälliger Sequenz (also an Hintergrundrauschen)
quantifiziert und dieser Beitrag nicht in der Korrelationsstärke
beinhaltet ist. Die Bestimmung der Parameter erfolgt über
einen mehrstufigen Schätzprozess (siehe Jacobs und Lewis,
1983; Dehnert et al., 2006).
Abbildung 1 fasst die Funktionsweise dieser rekursiven, durch
den DAr(p)-Prozess gegebenen Modellierung einer Symbolsequenz
schematisch zusammen.
Aus einer gegebenen DNA-Sequenz lassen sich nun die Prozessparameter
schätzen. Der sich so ergebende Parametervektor
α = {α k } stellt dann das ergebnis unserer Neufassung
einer Korrelationsanalyse dar: das Korrelationsprofil einer
DNA-Sequenz. unsere ersten Tests an ganzen Chromosomen
verschiedener eukaryotischer Spezies zeigten sehr klar, dass
0,1
0,08
0,06
0,04
0,02
Korrelationsstärke
Die mathematische suche nach verborgenen signalen im genom
H. sapiens:
Chr. 22
Chr. 21
Chr. 20
M. musculus:
Chr. 19
Chr. 18
Chr. 17
0 5
10 15 20
25 30
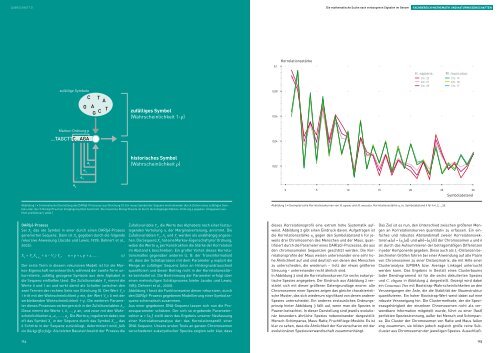
Abbildung 2 • exemplarische Korrelationskurven von H. sapiens und M. musculus. Korrelationsstärke α k vs. Symbolabstand k für k=1,2,…,30.
dieses Korrelationsprofil eine extrem hohe Systematik aufweist.
Abbildung 2 gibt einen eindruck davon. Aufgetragen ist
die Korrelationsstärke α k gegen den Symbolabstand k für jeweils
drei Chromosomen des Menschen und der Maus, quantifiziert
durch die Parameter eines DAr(30)-Prozesses, die aus
den chromosomalen Sequenzen geschätzt werden. Die Korrelationsprofile
der Maus weisen untereinander eine sehr hohe
Ähnlichkeit auf und sind deutlich von denen des Menschen
zu unterscheiden, die wiederum – trotz der etwas größeren
Streuung – untereinander recht ähnlich sind.
In Abbildung 3 sind die Korrelationskurven für sechs eukaryotische
Spezies angegeben. Der eindruck aus Abbildung 2 verstärkt
sich mit dieser größeren Datengrundlage enorm: alle
Chromosomen einer Spezies zeigen das gleiche charakteristische
Muster, das sich wiederum signifikant von denen anderer
Spezies unterscheidet. ein anderes erstaunliches Ordnungsprinzip
hinter Abbildung 3 fällt auf, wenn man die Spezies in
Paaren betrachtet. In dieser Darstellung sind jeweils evolutionär
besonders ähnliche Spezies nebeneinander dargestellt:
Mensch-Schimpanse, Maus-ratte, Fruchtfliege-Moskito. es ist
klar zu sehen, dass die Ähnlichkeit der Kurvenscharen mit der
evolutionären Speziesverwandtschaft zusammenhängt.
FAchbereich mAthemAtik und nAturwissenschAFten
Symbolabstand
Das Ziel ist es nun, den unterschied zwischen größeren Mengen
an Korrelationskurven quantitativ zu erfassen. ein einfaches
und robustes Abstandsmaß zweier Korrelationsvektoren
α(a) = {α k (a)} und α(b)={α k (b)} der Chromosomen a und b
ist durch das Aufsummieren der betragsmäßigen Differenzen
in jeder Komponente gegeben. Diese auch als L 1 -Distanzen bezeichneten
Größen führen bei einer Anwendung auf alle Paare
von Chromosomen zu einer Distanzmatrix, die mit Hilfe einer
Clusteranalyse (uPGMA bzw. Average Linkage) untersucht
werden kann. Das ergebnis in Gestalt eines Clusterbaums
(oder Dendrogramms) ist für die sechs diskutierten Spezies
und C. elegans in Abbildung 4 dargestellt. Gezeigt wird dabei
ein Consensus Tree mit Bootstrap-Wahrscheinlichkeiten an den
Verzweigungen der Äste, die die Stabilität der Baumstruktur
quantifizieren. ein hoher Bootstrap-Wert weist dabei auf eine
robuste Verzweigung hin. Die Clustermethode, der die Spezieszugehörigkeit
der einzelnen Chromosomen nicht als verwendbare
Information mitgeteilt wurde, führt zu einer (fast)
perfekten Speziestrennung, außer bei Mensch und Schimpanse.
Die Cluster der Chromosomen von ratte und Maus fallen
eng zusammen, sie bilden jedoch zugleich große reine Subcluster
aus Chromosomen der jeweiligen Spezies. Ausschließ-
115