Principles of cell signaling - UT Southwestern
Principles of cell signaling - UT Southwestern
Principles of cell signaling - UT Southwestern
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
39057_ch14_<strong>cell</strong>bio.qxd 8/28/06 5:11 PM Page 597<br />
Developing quantitative models <strong>of</strong> <strong>signaling</strong><br />
networks is a frontier in <strong>signaling</strong> biology. These<br />
models both help describe network function<br />
and pinpoint experiments to clarify mechanism.<br />
14.7<br />
Cellular <strong>signaling</strong><br />
pathways can be thought<br />
<strong>of</strong> as biochemical logic<br />
circuits<br />
Key concepts<br />
• Signaling networks are composed <strong>of</strong> groups <strong>of</strong><br />
biochemical reactions that function as<br />
mathematical logic functions to integrate<br />
information.<br />
• Combinations <strong>of</strong> such logic functions combine as<br />
<strong>signaling</strong> networks to process information at more<br />
complex levels.<br />
As introduced in the preceding section, processes<br />
that <strong>signaling</strong> pathways use to integrate and direct<br />
information to <strong>cell</strong>ular targets are strikingly analogous<br />
to the mathematical logic functions that are<br />
used to design the individual circuits <strong>of</strong> electronic<br />
computers. Indeed, there are biological equivalents<br />
<strong>of</strong> essentially all <strong>of</strong> the functional components<br />
that computer scientists and engineers<br />
consider in the design <strong>of</strong> computers and electronic<br />
control devices. To understand <strong>signaling</strong> pathways,<br />
it is, therefore, useful to consider groups <strong>of</strong><br />
reactions within a pathway as constituting logic circuits<br />
<strong>of</strong> the sort used in electronic computing, as<br />
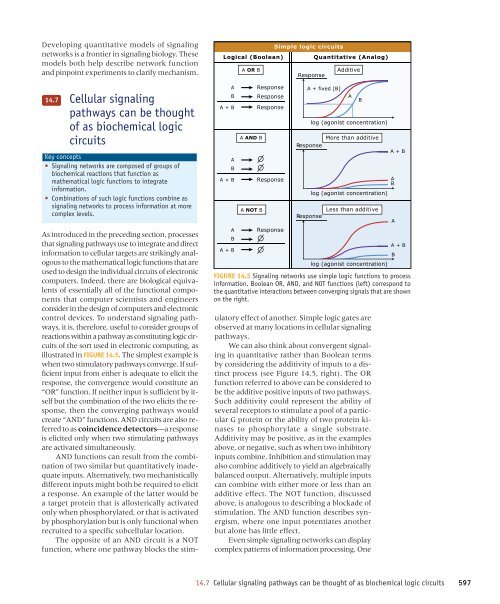
illustrated in FIGURE 14.5. The simplest example is<br />
when two stimulatory pathways converge. If sufficient<br />
input from either is adequate to elicit the<br />
response, the convergence would constitute an<br />
“OR” function. If neither input is sufficient by itself<br />
but the combination <strong>of</strong> the two elicits the response,<br />
then the converging pathways would<br />
create “AND” functions. AND circuits are also referred<br />
to as coincidence detectors—a response<br />
is elicited only when two stimulating pathways<br />
are activated simultaneously.<br />
AND functions can result from the combination<br />
<strong>of</strong> two similar but quantitatively inadequate<br />
inputs. Alternatively, two mechanistically<br />
different inputs might both be required to elicit<br />
a response. An example <strong>of</strong> the latter would be<br />
a target protein that is allosterically activated<br />
only when phosphorylated, or that is activated<br />
by phosphorylation but is only functional when<br />
recruited to a specific sub<strong>cell</strong>ular location.<br />
The opposite <strong>of</strong> an AND circuit is a NOT<br />
function, where one pathway blocks the stim-<br />
Logical (Boolean)<br />
A<br />
B<br />
A + B<br />
A<br />
B<br />
A + B<br />
A<br />
B<br />
A + B<br />
A OR B<br />
A AND B<br />
A NOT B<br />
Response<br />
Response<br />
Response<br />
Response<br />
Response<br />
Simple logic circuits<br />
Response<br />
Quantitative (Analog)<br />
A + fixed [B]<br />
Response<br />
Response<br />
Additive<br />
ulatory effect <strong>of</strong> another. Simple logic gates are<br />
observed at many locations in <strong>cell</strong>ular <strong>signaling</strong><br />
pathways.<br />
We can also think about convergent <strong>signaling</strong><br />
in quantitative rather than Boolean terms<br />
by considering the additivity <strong>of</strong> inputs to a distinct<br />
process (see Figure 14.5, right). The OR<br />
function referred to above can be considered to<br />
be the additive positive inputs <strong>of</strong> two pathways.<br />
Such additivity could represent the ability <strong>of</strong><br />
several receptors to stimulate a pool <strong>of</strong> a particular<br />
G protein or the ability <strong>of</strong> two protein kinases<br />
to phosphorylate a single substrate.<br />
Additivity may be positive, as in the examples<br />
above, or negative, such as when two inhibitory<br />
inputs combine. Inhibition and stimulation may<br />
also combine additively to yield an algebraically<br />
balanced output. Alternatively, multiple inputs<br />
can combine with either more or less than an<br />
additive effect. The NOT function, discussed<br />
above, is analogous to describing a blockade <strong>of</strong><br />
stimulation. The AND function describes synergism,<br />
where one input potentiates another<br />
but alone has little effect.<br />
Even simple <strong>signaling</strong> networks can display<br />
complex patterns <strong>of</strong> information processing. One<br />
A<br />
log (agonist concentration)<br />
More than additive<br />
log (agonist concentration)<br />
Less than additive<br />
log (agonist concentration)<br />
B<br />
A + B<br />
A<br />
B<br />
A<br />
A + B<br />
B<br />
FIGURE 14.5 Signaling networks use simple logic functions to process<br />
information. Boolean OR, AND, and NOT functions (left) correspond to<br />
the quantitative interactions between converging signals that are shown<br />
on the right.<br />
14.7 Cellular <strong>signaling</strong> pathways can be thought <strong>of</strong> as biochemical logic circuits 597