Tesi Specializzazion.. - Ingegneria Strutturale - Politecnico di Milano

POLITECNICO DI MILANO
Scuola di Specializzazione in
COSTRUZIONE IN CEMENTO ARMATO
“F.lli Pesenti”
MODELLAZIONE TRIDIMENSIONALE DI
STRUTTURE IN C.A. E C.A.P. IN CAMPO NON
LINEARE
Relatore:
Correlatore:
Prof. Franco Bontempi
Ing. Fabio Biondini
Tesi di Specializzazione
Ing. Luca Sgambi
Anno Accademico 1999-2000

Oltre al prof. Bontempi ed all’ing. Biondini che mi hanno seguito in questi due anni di
permanenza alla scuola “f.lli Pesenti” offrendomi spunti di studio e di riflessione su
molteplici argomenti, desidero ringraziare il prof. Malerba per la pazienza e la
disponibilità a discutere i temi che ho trattato in questo lavoro.

Indice
Indice
Cap. 1 Introduzione al metodo degli elementi finiti
I fenomeni fisici 1
Le equazioni differenziali alle derivate parziali 3
Necessità della risoluzione numerica 6
La formulazione debole per problemi stazionari 8
PSV applicato ad un continuo suddiviso in elementi 11
Convergenza del metodo 15
Proprietà delle funzioni di forma 16
Cap. 2 Formulazione dell’elemento finito tridimensionale
Formulazione dell’elemento compatibile 17
La rigidezza dell’elemento compatibile 26
L’integrazione selettiva 27
Le funzioni di forma incompatibili 32
I vincoli elastici concentrati 34
Deformazioni anelastiche 35
Armatura embedded 36
L’armatura diffusa 39
Cap. 3 Legami costitutivi e problema non lineare
La non linearità di materiale
41
Definizione della variabile di danno
42
Definizione dello stato di sforzo effettivo
44
Ipotesi d’equivalenza nelle deformazioni
45
La legge d’evoluzione di Mazars
46
La legge d’evoluzione di Cervera
51
La legge d’evoluzione di Rizzi
55
La legge d’evoluzione proposta per il modello isotropo
56
Un legame ortotropo 57
Legami costitutivi dell’acciaio 60
Cenni sulla regolarizzazione della risposta non lineare 62
Metodo della secante per la soluzione di problemi non lineari 63
_____________________________________________________________________________________________
I

Indice
Cap. 4 Applicazioni in campo elastico lineare 68
Patch Test per l’elemento solido integrato in modo selettivo 69
Patch Test per l’elemento solido con funzioni di forma non compatibili 75
Analisi di una mensola snella 77
Analisi di una trave doppiamente incastrata 81
Studio della deformabilità trasversale e dell’ingobbimento sezionale di
un elemento in parete sottile a profilo rettangolare chiuso 92
Patch Test per l’elemento solido con acciaio diffuso 100
Patch Test per l’elemento solido con acciaio embedded 103
Patch Test per l’elemento solido presollecitato 105
Pilastro soggetto a peso proprio 107
Studio di una pila da ponte a profilo misto in campo elastico lineare 109
Cap. 5 Applicazioni in campo elastico non lineare 118
Prove di compressione monoassiale 119
Dominio di rottura di Kupfer 122
Dominio di rottura di Bresler-Pister 130
Pannello soggetto a taglio puro 131
Trave di Bresler-Scordelis 135
Studio di una pila da ponte a profilo misto in campo non lineare 142
Conclusioni 162
Appendice A : I codici di calcolo sviluppati 164
Appendice B : Bibliografia 181
_____________________________________________________________________________________________
II

Introduzione al metodo degli Elementi Finiti Cap. 1
Capitolo 1
Introduzione al metodo degli Elementi Finiti
1. I fenomeni fisici
Moltissimi fenomeni fisici, modellati matematicamente assumono l’aspetto di una o più equazioni
differenziali ordinarie o alle derivate parziali. Solitamente si tratta di equazioni la cui soluzione in
forma chiusa riesce solo per geometrie semplici e con drastiche semplificazioni. Si pensi al problema
della torsione di una barra alla De Saint Venant, la soluzione in forma chiusa è facile solo se la
sezione della barra è di tipo ellittico, per un profilo generico il problema diviene estremamente
complicato. Risulta spesso necessario ricorrere a delle soluzioni approssimate.
I fenomeni fisici si possono si possono suddividere schematicamente in stazionari e non stazionari,
per descrivere questi ultimi, l’equazioni che regolano il problema avranno anche una dipendenza
dalla variabile temporale.
I fenomeni stazionari più comuni sono regolati dalle seguenti equazioni [L1, L10]:
2
L’equazione armonica K ⋅∇
Φ + Q = 0 che descrive fenomeni di trasporto per diffusione come la
trasmissione di calore nei solidi, il trasporto di materia, i moti di filtrazione, la deformata di una
membrana, la torsione di una barra prismatica, il moto di un fluido ideale, l’elettrostatica, la
magnetostatica.
2
L’equazione di Helmoltz ∇ Φ + λ ⋅ Φ = 0 dove il termine sorgente va sostituito un termine
proporzionale all’incognita cercata. Questa equazione governa fenomeni che possono divenire
instabili, per cui il principale problema riguarda il calcolo dei valori critici del parametro λ ≥ 0.
Fenomeni di questo genere riguardano, ad esempio, l’instabilità elastica.
1

Introduzione al metodo degli Elementi Finiti Cap. 1
∂ ∂Φ ∂ ∂Φ ∂ ∂Φ
L’equazione quasi armonica ( K
x
⋅ ) + ( K
y
⋅ ) + ( K
z
⋅ ) + Q = 0 definita da un
∂x
∂x
∂y
∂y
∂z
∂z
coefficiente K diverso nelle direzioni x, y, z. Equazioni di questo genere riguardano, ad esempio, la
trasmissione di calore in un mezzo ortotropo e la lubrificazione con moto laminare (equazione di
Reynolds).
4
L’equazione biarmonica K ⋅∇
Φ + Q = 0 che regola, ad esempio, il problema degli elementi
inflessi, travi e piastre, ma anche i problemi di elasticità piana, scritti assumendo come incognita la
funzione di Airy.
I fenomeni non stazionari più comuni si studiano a partire dall’equazione armonica, aggiungendo o la
derivata prima temporale o la derivata seconda.
Equazioni con la derivata prima temporale K ⋅∇
2
∂Φ
Φ + Q = b ⋅
∂t
regolano una serie di fenomeni
transitori (b è definito come il termine di immagazzinamento) quali il transitorio termico, il flusso di
Blasius (comportamento di un fluido in un mezzo seminfinito soggetto ad un movimento della base
su cui si appoggia), il consolidamento di un terreno, l’equazione di Schrodinger (moto libero di una
particella in meccanica quantistica).
Equazioni con la derivata seconda temporale
2
2 ∂ Φ ∂Φ
⋅∇
Φ + Q = µ ⋅ + h ⋅ + f
∂t
∂t
K
2
rappresentano numerosi fenomeni fisici quali, la propagazione di onde longitudinali in una barra, la
propagazione di onde acustiche, la propagazione di onde superficiali in acque poco profonde, la
propagazione di onde elettromagnetiche in un dielettrico.
⋅ Φ
2

Introduzione al metodo degli Elementi Finiti Cap. 1
2. Le equazioni differenziali alle derivate parziali
Le equazioni viste in precedenza, sono equazioni del secondo ordine, intendendosi per ordine quello
della derivata massima che vi compare. Ad esempio, un’equazione del secondo ordine ad un solo
2 2 2
∂Φ ∂Φ ∂ Φ ∂ Φ ∂ Φ
parametro incognito e due variabili indipendenti è del tipo F ( x,
y,
Φ,
, , , , ) = 0 .
2
2
∂x
∂y
∂x
∂x∂y
∂y
La possibilità di descrivere un fenomeno fisico con una equazione alle derivate parziali, è legata alla
possibilità di determinare univocamente una particolare soluzione fra le infinite che ne costituiscono
l’integrale generale [L1, L21]. Ciò è possibile se all’integrale generale vengono imposte opportune
condizioni restrittive relative al comportamento della soluzione sulla frontiera del dominio. Per
problemi stazionari Φ deve soddisfare a condizioni al contorno di tipo essenziale e di tipo naturale.
S 1
A : ∇ 2 Φ =
f
n
S 2
Figura 1.1: Condizioni al contorno.
Se 2m è il massimo ordine di derivazione nell’equazione differenziale, le condizioni essenziali (di
Dirichlet) si applicano al contorno (S 1 ) sulle derivate di ordine r, con 0 ≤ r ≤ m , della funzione
incognita; le condizioni di tipo naturale (di Neumann o di tipo convettivo) si applicano invece su (S 2 )
alle derivate di ordine p, con m ≤ p ≤ 2m
.
Problema in stato piano di sforzo 2m = 2
Problema di elemento inflesso 2m = 4
3

Introduzione al metodo degli Elementi Finiti Cap. 1
Come esempio si esamini il problema di un’asta tesa.
F
l
Figura 1.2: Asta tesa.
2
d u
L’equazione che governa il fenomeno è EA = p . Le condizioni al contorno si pongono in x = 0,
2
dx
ed un x = l, essendo il contorno dell’asta rappresentato da soli questi due punti. In x = 0 si dovranno
porre delle condizioni al contorno di tipo essenziale:
u = 0
Condizioni di Dirichlet
x=0
In x = l si dovranno porre delle condizioni al contorno di tipo naturale:
du
EA
dx
x=
l
= F
Condizioni di Neumann
Problemi in cui tutto il contorno è vincolato ad assumere valori essenziali o naturali sono definiti
problemi dei valori al contorno. A seconda del tipo di equazione e delle condizioni al contorno, il
problema può non avere soluzione, avere una soluzione, più soluzioni, infinite soluzioni.
Per i problemi non stazionari si deve imporre anche una condizione ai valori iniziali sulla funzione
incognita, si avranno quindi condizioni miste, sia al contorno che iniziali. Poiché le equazioni non
stazionarie, ammettono soluzioni che evolvono nel tempo ed il loro comportamento ad un certo
istante è determinato da quello relativo agli istanti precedenti, un problema dei valori al contorno che
prescrive arbitrariamente la soluzione in più istanti separati non è fisicamente ammissibile.
4

Introduzione al metodo degli Elementi Finiti Cap. 1
Sia L() un operatore differenziale, limitandoci ad una generica equazioni di second’ordine lineare
con due variabili indipendenti, si può porre:
2
2
2
∂ Φ ∂ Φ ∂ Φ ∂Φ ∂Φ
L ( Φ)
= a ⋅ + b ⋅ + c ⋅ + d ⋅ + e ⋅ + f ⋅ Φ = g
(1.1)
2
2
∂x
∂x∂y
∂y
∂x
∂y
una classificazione matematica delle EDP si effettua sul segno del discriminante ∆ = b 2 – 4ac, si ha
infatti:
se ∆ < 0
se ∆ = 0
se ∆ > 0
l’equazione si dice ellittica
l’equazione si dice parabolica
l’equazione si dice iperbolica
2 2
∂ ∂
I problemi stazionari sono retti da equazioni di tipo ellittico, L()
= + ; esempio di un
2 2
∂x
∂y
problema parabolico è l’equazione del calore in un transitorio termico (con derivata prima
2
∂ ∂
temporale), L() = −k
⋅ + ; esempio di un problema iperbolico è la propagazione di onde lungo
2
∂x
∂t
2 2
2 ∂ ∂
una barra L()
= −c
⋅ + . Si dimostra (eseguendo dei cambi di variabile) che un’equazione
2 2
∂x
∂t
iperbolica possiede due famiglie di linee caratteristiche (linee sulle quali si propaga un’eventuale
discontinuità della soluzione), un’equazione parabolica ha solo una famiglia di linee caratteristiche,
un’equazione ellittica non ha linee caratteristiche. Non avendo linee caratteristiche, i problemi
associati ad un operatore ellittico (esempio asta in trazione, membrana…) non possono avere
soluzioni discontinue.
5

Introduzione al metodo degli Elementi Finiti Cap. 1
3. Necessità della risoluzione numerica
In generale, non è possibile ricavare per via analitica una soluzione dalla (1.1). I metodi di
integrazione analitica disponibili (trasformate di Fourier e di Laplace, sviluppo in serie di
autofunzioni, separazione delle variabili) sono di limitata apllicabilità. Peraltro, anche nel caso che si
conoscesse l’integrale generale, non è poi detto che si riesca a determinare un integrale particolare.
Per ottenere quest’ultimo bisogna infatti assegnare opportune condizioni sulla soluzione (e/o sulle
sue derivate) sulla frontiera del dominio.
Da ciò segue l’importanza di disporre di metodi numerici che permettano di costruire
un’approssimazione
Φ
n
della soluzione esatta Φ e di valutare, in una qualche norma, l’errore
Φ n
− Φ che si commette sostituendo alla soluzione esatta quella approssimata. L’intero positivo N
denota la dimensione (finita) del problema approssimato.
Vi sono vari metodi utilizzati per la risoluzione numerica di una EDP. Molto comune è il metodo
delle differenze finite che approssima l’equazione differenziale mediante differenze finite, lasciando
il sistema continuo. I svantaggi del metodo delle differenze finite si avvertono nell’approssimazione
di un dominio bidimensionale, che può avvenire solamente in modo rozzo con celle quadrate, ed
all’atto dell’imposizione delle condizioni al contorno sulle derivate, che richiedono l’introduzione
artificiosa di altri nodi. Il metodo degli elementi finiti è il duale del metodo delle differenze finite, nel
senso che mentre il secondo approssima le equazioni differenziali applicate al continuo intatto, il
primo discretezza il continuo a cui applica le equazioni esatte. L’utilizzo di elementi distorti porta ad
una approssimazione molto precisa delle frontiere, inoltre applicando le equazioni esatte in forma
variazionale, le condizioni al contorno naturali sono automaticamente soddisfatte, e quelle essenziali
si impongono all’atto della soluzione del sistema. Il metodo delle differenze finite torna utile nei
problemi non stazionari, (sia parabolici che iperbolici) dove le equazioni differenziali vengono
approssimate col metodo delle differenze finite nella variabile temporale (metodi di Eulero per le
equazioni paraboliche, metodi di Newmark per le equazioni iperboliche).
Un secondo metodo di risoluzione numerica di una EDP è il metodo di Rayleigh-Ritz. Questo
metodo, come il metodo degli Elementi Finiti, risolve la EDP minimizzando il funzionale ad essa
associata (se ne discuterà nel prossimo paragrafo).
6

Introduzione al metodo degli Elementi Finiti Cap. 1
La variabile Φ viene approssimata con una combinazione lineare di funzioni note N i e parametri
incogniti
Φ
i
Φ =
n
∑ N i
i=
1
⋅ Φ
i
(1.2)
le funzioni N i devono essere scelte in modo da soddisfare le condizioni essenziali nell’intero dominio
del sistema. Sostituita la funzione approssimata nel funzionale, se impone la stazionarietà. Ne risulta
un sistema di n equazioni nelle n incognite
Φ
i
.
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
∂Π
∂Φ
1
⎤
⎥
⎥
⎥
⋮ ⎥ = 0 → K ⋅ Φ = F
(1.3)
⎥
⎥
∂Π ⎥
∂Φ
⎥
n ⎦
Poiché questo metodo richiede che nella scelta delle funzioni interpolanti siano soddisfatte le
condizioni essenziali nell’intero dominio, il metodo di Rayleigh-Ritz trova applicazione soltanto con
geometrie particolarmente semplici (ad esempio nello studio dell’instabilità per imbozzamento di
lastre rettangolari).
Il metodo degli elementi finiti è una sottoclasse del metodo di Rayleigh-Ritz, in cui le funzioni
interpolanti N i sono definite non nell’intero dominio A, ma in sottodomini Ae, detti elementi finiti,
ottenuti per discretizzazione di A. In questo modo si supera lo svantaggio del metodo di Rayleigh-
Ritz, che era limitato a domini di forma semplice. Il metodo degli Elementi Finiti fu introdotto per la
prima volta dal prof. Turner nel 1956 per l’analisi di problemi di elasticità piana come sviluppo del
calcolo matriciale.
7

Introduzione al metodo degli Elementi Finiti Cap. 1
4. La formulazione debole per problemi stazionari
La formulazione forte (formulazione differenziale) non è in genere adeguata, alla ricerca della
soluzione fisica del problema per l’elevato ordine di derivazione richiesto. Come esempio si
consideri l’equazione di un filo elastico. Questa ricavata considerando il carico distribuito su tutta la
linea (equazione della linea funicolare), se ho un carico concentrato la soluzione fisica esiste, ma non
è soluzione del modello matematico assunto (la soluzione è continua ma non derivabile con
continuità). Serve una formulazione alternativa che consenta di ridurre l’ordine di derivazione
richiesto alla funzione incognita. Tramite una serie di passaggi matematici (tra cui la moltiplicazione
per una funzione test ed un’integrazione per parti) si passa da un problema differenziale di ordine 2m
ad uno in forma integrale di ordine m. Questo problema viene definito come formulazione debole del
problema differenziale. Ad esempio il problema del filo elastico in formulazione forte:
2
d Φ
− =
2
dx
w(0)
= 0
f ( x)
per
Φ(
l)
= 1
0 < x < l
viene ricondotto alla formulazione debole: cercare Φ nello spazio V tale che
l
l
⎡1
dv
⎤
2
J ( Φ)
= min J ( v)
= min⎢
∫ ( ) dx − ∫ v ⋅ fdx⎥
per ogni v (funzione test) appartenente allo spazio V.
⎣2
dx
0 0 ⎦
se Φ è soluzione del problema variazionale, allora la formulazione forte è equivalente alla debole.
Bisogna definire ora qual è lo spazio in cui si cerca la soluzione. Dato che si deve integrare una
funzione derivata m volte, si potrebbe imporre che V sia lo spazio C m (derivabile con continuità sino
all’ordine m) tuttavia si è visto che la derivata di ordine m può non essere continua. Se m è l’ordine
di derivazione presente nel problema variazionale, si dimostra che lo spazio V in cui cercare la
soluzione è lo spazio di Sobolev H m . A differenza dello spazio C m , spazio delle funzioni continue con
derivata continua sino all’ordine m, lo spazio H m contiene anche le funzioni continue ma con derivata
di ordine m non continua in un numero finito di punti [L10].
8

Introduzione al metodo degli Elementi Finiti Cap. 1
Nel caso di problemi di elasticità il funzionale da minimizzare sarà l’energia potenziale elastica, e lo
spazio delle funzioni test V, racchiude tutte le funzioni di spostamento ammissibili.
Si può infatti dimostrare che:
tra tutti i campi di spostamento ammissibili, quello che soddisfa le condizioni di equilibrio rende
l’energia potenziale del sistema stazionaria e minima.
Da questo principio, discendono metodi di soluzione algebrica, per problemi di elasticità, che
interpolano la funzione spostamento, da cui il nome di metodo degli spostamenti.
Si possono formulare metodi basati sulla stazionarietà di altri funzionali. Se il principio di minima
energia potenziale, permetteva di ottenere una formulazione variazionale che determina la rigidezza
di un sistema, il principio di minima energia complementare ne determina la flessibilità.
Π
p
=
1
2
∫
V
ε
T
⋅ D ⋅ε
⋅ dV −
∫
V
s
T
⋅ F ⋅ dV −
∫
Γf
s
T
⋅ f
⋅ dΓ
(EPT) (1.4)
Π
c
=
1
2
∫
V
σ
T
⋅ D
−1
⋅σ
⋅ dV −
∫
Γf
f
T
⋅t
⋅ dΓ
(ECT) (1.5)
Il principio afferma che:
tra tutti gli stati tensionali che soddisfano le condizioni di equilibrio all’interno del sistema e le
tensioni imposte sul contorna, lo stato di tensione che soddisfa anche la congruenza rende
stazionaria e minima l’energia complementare totale.
Da questo principio discende il metodo delle forze. Pensando ad una soluzione automatizzata, si fa
notare che si ottiene un metodo più complesso e meno intuitivo, rispetto al metodo degli spostamenti.
Infatti, anche se il calcolo delle tensioni risulta più accurato, la costruzione di un modello di forze
equilibrato, è molto più complicato rispetto ad una costruzione di un modello di spostamenti
compatibile.
9

Introduzione al metodo degli Elementi Finiti Cap. 1
Mostriamo ora per il caso di una mensola su di un terreno elastico che la formulazione debole
equivale alla formulazione forte. L’equazione differenziale della trave è data da:
EJw
IV
− p + k
f
w = 0
dove con w si è indicato lo spostamento trasversale della trave, con p un carico distribuito e con K f la
costante di sottofondo. Le condizioni essenziali si impongono su w e w I al contorno vincolato
cinematicamente. L’energia potenziale è somma dell’energia di deformazione elastica della trave e
delle molle che schematizzano il terreno meno il lavoro dei carichi esterni:
Π(
w)
=
l
∫
EJ
2
k
w
l 2 l
II 2
f
( w ) dx + ∫ dx − ∫ pwdx
2
0 0
0
Per minimizzare il funzionale si impone che la variazione prima sia nulla:
l
II II
( EJw δw
+ k wδw
− p )
δ Π( w)
= ∫ f
δw dx = 0
0
Si integra ora per parti l’energia flessionale, tenendo presente che δw II = δ(δw I ) I
l
II II
II I
l
∫ EJw δ w dx = EJw δw
−
0 ∫
0
l
0
EJw
III
δw
I
dx
e si integra ancora per parti l’ultimo termine della
l
III I
III
l
∫ EJw δ w dx = EJw δw
−
0 ∫
0
l
0
EJw
IV
δwdx
10

Introduzione al metodo degli Elementi Finiti Cap. 1
si ottiene che
l
∫
0
II
EJw δw
II
l
dx = ∫ EJw
0
IV
δwdx
+
II I
EJw δw
l
0
−
EJw
III
δw
l
0
la variazione prima diviene quindi:
l
IV
II I
l
III
l
∫ ( EJw − p + k
f
w) δ wdx + EJw δw
− EJw δw
= 0
0
0
0
Essendo ora la variazione dw arbitraria, ed ipotizzando che le condizioni essenziali siano di incastro
all’estremo x = 0 (le variazioni per x = 0 devono quindi essere nulle) si ottengono le equazioni:
EJw
IV
− p + k
f
w = 0
equazione differenziale di equilibrio
II
III
EJw = 0 EJw = 0 condizioni al contorno naturali
l
l
5. PSV applicato ad un continuo suddiviso in elementi
Occupiamoci ora della meccanica del continuo ed applichiamo il principio degli spostamenti virtuali
ad un continuo suddiviso in elementi. Consideriamo il generico elemento ‘e’:
e
S f,e
S s,e
S i,e
Figura 1.3: Divisione di un continuo in elementi finiti
11

Introduzione al metodo degli Elementi Finiti Cap. 1
L’elemento possiede in generale un tratto di superficie S s,e in cui sono applicate le condizioni al
contorno essenziali, un tratto S f,e in cui sono applicate le condizioni al contorno naturali, ed un tratto
S i,e in comune con gli altri elementi (superficie d’interfaccia).
Il funzionale energia potenziale elastica per l’elemento ‘e’ si scrive:
Π
p
∫
∫
∫
( s)
= ε ⋅σ
dV − s ⋅ F dV − s ⋅ f dS − s ⋅ f dS − s ⋅t
dS
(1.6)
Ve
T
Ve
T
Sf , e
T
∫
Ss,
e
T
∫
Si,
e
T
Dove t sono le tensioni interelementari, f le reazioni vincolari, f le forze di superficie, F le forze di
volume. Nella classe delle soluzioni congruenti, il funzionale Π p (s) è stazionario in corrispondenza di
una soluzione equilibrata. La stazionarietà viene imposta imponendo che sia nulla la variazione delle
funzionale per una variazione congruente δs:
∫
Ve
T
∫
∫
δ ε ⋅σ
dV = δ s ⋅ F dV + δ s ⋅ f dS + δ s ⋅ f dS + δ s ⋅ t dS
(1.7)
Ve
T
Sf , e
T
∫
Ss,
e
T
∫
Si,
e
T
Dovendo la variazione verificare la congruenza, δ s = 0 sul contorno dove si impongono le condizioni
essenziali (S s ,e) per cui il terzo integrale a secondo membro della (1.7) deve essere nullo. La
continuità del campo di spostamenti richiede inoltre che non vi siano lacerazioni e compenetrazioni
tra gli elementi (δs e s sono gli stessi sulla superficie d’interfaccia per elementi adiacenti).
Sommando sui vari elementi:
∑ ∫
e
Ve
T
∑ ∫
∑ ∫
δ ε ⋅σ
dV = δ s ⋅ F dV + δ s ⋅ f dS + δ s ⋅t
dS
(1.8)
e
Ve
T
e
Sf , e
T
∑ ∫
e
Si,
e
T
ma dato che le forze interelementari tra un elemento ed il suo adiacente sono uguali in modulo ed
opposte in segno per il principio di azione e reazione, e che gli spostamenti dell’interfaccia devono
essere continui, la somma del lavoro delle forze interelementari risulta nullo.
12

Introduzione al metodo degli Elementi Finiti Cap. 1
∑ ∫
e Si,
e
T
δ s ⋅t
dS ≡ 0 (ipotesi di continuità degli spostamenti sull’interfaccia) (1.9)
L’equazione si riduce quindi a:
∑ ∫
e
Ve
T
∑ ∫
T
∑ ∫
δ ε ⋅σ
dV = δ s ⋅ F dV + δ s ⋅ f dS
(1.10)
e Ve
e Sf , e
T
Si assumono ora come incognite gli spostamenti in un numero finito di punti, detti ‘nodi’. Questi
punti formano un reticolo che suddividono la struttura in un numero finito di elementi. Gli
spostamenti all’interno degli elementi vengono espressi mediante interpolazione degli spostamenti
nodali corrispondenti all’elemento (S).
s = N ⋅ S
(1.11)
ε = L(
s)
= L(
N)
⋅ S = B ⋅ S
(1.12)
σ = D ⋅ε
= ( D ⋅ B)
⋅ S = E ⋅ S
(1.13)
Dove N è la matrice delle funzioni di forma, B è la matrice di congruenza interna dell’elemento, D
è la matrice delle costanti elastiche ed L () è un operatore di congruenza che lega gli spostamenti alle
deformazioni, la sua forma dipende dal tipo di problema in esame. Le quantità di sinistra dipendono
dalla posizione all’interno dell’elemento tramite le matrici N , B , E in cui vi è la dipendenza dalle
coordinate. Il vettore S raccoglie le incognite nodali. Lo spostamento è stato interpolato tramite delle
funzioni di forma che dipendono strettamente dal tipo di elemento finito usato. La variazione è:
δ ε = B ⋅δ S
(1.14)
13

Introduzione al metodo degli Elementi Finiti Cap. 1
per cui la (1.8) si può scrivere come:
∑ ∫
e
Ve
T
T
∑ ∫
T
T
δ S ⋅ B ⋅ D ⋅ B ⋅ S dV = δ S ⋅ N ⋅ F dV + δ S ⋅ N ⋅ f dS
(1.15)
∑ ∫
e Ve
e Sf , e
T
T
portando i vettori delle incognite nodali fuori dagli integrali si ottiene:
T
∑ ∫
T
∑ ∫
T
δ S ⋅ B ⋅ D ⋅ B dV ⋅ S = δ S ⋅ N ⋅ F dV + δ S ⋅ N ⋅ f dS
(1.16)
e
Ve
T
∑ ∫
e Ve
e Sf , e
T
T
dovendo questa essere verificata per una generica variazione, deve essere:
∑ ∫
e
Ve
B
T
⋅ D ⋅ B
dV ⋅ S =
∑ ∫
N
T
⋅ F
dV +
∑ ∫
e Ve
e Sf , e
N
T
⋅ f
dS
(1.17)
Interpretando le sommatorie come l’operazione di assemblaggio, si giunge al sistema lineare:
K ⋅ S = F + f
(1.18)
t
t
t
t
dove S t raccoglie tutti gli spostamenti incogniti, K t è la matrice di rigidezza totale, F t e f t sono le forze
nodali equivalenti totali.
∑
∑ ∫
K = K = B ⋅ D ⋅ B dV
(1.19)
t
e
e
e
Ve
T
∑
∑ ∫
F = F = N ⋅ F dV
(1.20)
t
e
e
e
Ve
T
f
t
=
∑
e
f
e
=
∑ ∫
e
Sf , e
N
T
⋅ f
dS
(1.21)
Ogni elemento finito possiede le sue particolari matrici.
14

Introduzione al metodo degli Elementi Finiti Cap. 1
6. Convergenza del metodo
I criteri di convergenza del metodo degli elementi finiti sono stati formulati da Bazeley nel 1967.
Condizione necessaria perché si abbia convergenza è che le funzioni di forma assunte soddisfino il
requisito di completezza. Se il massimo ordine di derivazione nel funzionale è m, le funzioni di
forma devono essere dei polinomi completi di grado m. Questo perché l’elemento deve poter
rappresentare stati di deformazione costante e stati di deformazione nulla (moti rigidi).
Nel caso di elementi di lastra (stato piano di sforzo), il massimo ordine di derivazione nel funzionale
è 1, per cui è sufficiente un polinomio di tipo u
α + α ⋅ x + ⋅ y , v α + α ⋅ x + ⋅ y
=
1 2
α
3
=
4 5
α
6
E’ chiaro che lo stato di deformazione costante è sicuramente rappresentato, essendo le funzioni
spostamento lineari e complete. I moti di traslazione nei versi coordinati vengono rappresentati si
hanno quando α
2
= α
3
= α
5
= α
6
= 0 , i moti rotatori quandoα 1
= α
2
= α
4
= α
6
= 0 e α
3
= −α
5
.
Se alla completezza viene aggiunta la condizione di compatibilità (o conformità) si dimostra che la
convergenza è assicurata in modo monotono. Per avere compatibilità vi deve essere continuità C m
all’interno dell’elemento e continuità C m-1 all’interfaccia tra due elementi. Per problemi di elasticità
piana sono sufficienti funzioni con continuità C 1 all’interno e C 0 all’interfaccia, nel caso di elementi
inflessi però il requisito sale a C 2 all’interno e C 1 all’interfaccia, condizione abbastanza facile da
rispettare nel caso di elementi tipo trave, più difficile per elementi di tipo piastra o guscio.
Per un elemento compatibile e completo la convergenza è assicurata in modo monotono. Inoltre se si
esamina un parametro nodale avente una sorgente concentrata (forza concentrata) nello stesso nodo,
la convergenza risulta dal basso. Se la sorgente è di tipo diffuso (forze di volume), la convergenza è
sempre monotona, ma può avvenire dal basso o dall’alto senza regole precise.
La completezza è una caratteristica essenziale per una corretta scelta delle funzioni interpolanti. La
compatibilità può in parte venire disattesa, senza pregiudicare la convergenza del metodo. Elementi
incompatibili si usano, ad esempio, nell’analisi di piastre e gusci (elementi ACM, BCIZ). Questi
elementi vanno sottoposti al cosiddetto Patch-Test: un’indagine per verificare la convergenza di un
elemento introdotta per la prima volta dal prof. Irons [L1, L5, L10, L11]. Se la condizione di
completezza è verificata per il singolo elemento, non è detto, infatti, che lo sia anche per gli elementi
assemblati.
15

Introduzione al metodo degli Elementi Finiti Cap. 1
Il Patch-Test consiste nel sottoporre una maglia non regolare di pochi elementi con almeno un nodo
interno ad uno stato di deformazione noto e verificare la bontà del risultato.
7. Proprietà delle funzioni di forma.
Gli elementi finiti hanno una forma che dipende dal problema da esaminare. Elementi
monodimensionali vengono usati per problemi con una sola variabile indipendente; elementi
bidimensionali, di forma triangolare e quadrangolare, per problemi con 1 o 2 variabili indipendenti
(piastre o lastre); elementi tridimensionali, di forma tetraedrica, prismatica ed esaedrica, per problemi
con 3 variabili indipendenti. Gli elementi sono collegati tra loro in punti particolari, detti nodi.
All’elemento finito è associato il concetto di discretizzazione del continuo, operazione mediante la
quale il dominio di definizione viene suddiviso in una maglia di elementi finiti. Il contorno
dell’elemento può essere approssimato in modo accurato usando elementi con lati curvi. La funzione
incognita viene interpolata tramite una combinazione lineare di funzioni di forma, definite per ogni
nodo dell’elemento. Le funzioni di forma devono possedere le seguenti proprietà [L1, L5]:
- La funzione di forma
calcolata negli altri nodi.
e
N
i
relativa al nodo i dell’elemento, vale 1 se calcolata nel nodo i e 0 se
- Per un generico elemento ad n nodi, la somma delle funzioni di forma deve essere uguale ad 1
(condizione di completezza).
- Il valore delle funzioni di forma dell’elemento e è nullo al di fuori dell’elemento e.
- Perché l’elemento sia compatibile la soluzione approssimata deve essere C m all’interno
dell’elemento e C m-1 sui bordi.
Il polinomio interpolante deve poi essere scelto in modo che:
- Il numero di termini del polinomio deve essere uguale al numero dei gradi di libertà associati
all’elemento. Se così non fosse il polinomio interpolante non sarebbe unico. Se ci sono più gdl per
nodo, bisogna considerare i gdl indipendenti tra loro.
- I termini polinomiali debbono essere simmetrici rispetto all’asse di simmetria del triangolo di
Pascal.
16

Formulazione dell’elemento finito tridimensionale Cap. 2
Capitolo 2
Formulazione dell’elemento finito tridimensionale
1. Formulazione dell’elemento finito compatibile
Per l’analisi ad elementi finiti di corpi solidi, sono disponibili 3 famiglie di elementi. Gli elementi
tetraedrici, che sono la generalizzazione nello spazio degli elementi triangolari piani, gli elementi
esaedrici, che sono la generalizzazione degli elementi quadrilateri piani e gli elementi prismatici, che
sono una combinazione di elementi triangolari e quadrilateri. In questo lavoro si sono utilizzati
elementi finiti esaedrici a 8 nodi.
ρ
1
z
y
3
2
4
6
5
8
1
5
2 6
4 8
η
ξ
x
7
3
7
Elemento reale
Elemento parente
Figura 2.1: Elemento esaedrico a 8 nodi.
Ogni nodo dell’elemento possiede 3 gradi di libertà, per cui la matrice di rigidezza del singolo
elemento risulterà una 24 x 24. Si può fin d’ora notare come l’estensione da elementi finiti piani ai
corrispondenti elementi solidi, non comporta grosse novità dal punto di vista teorico, ma causa un
sostanziale aumento delle incognite e quindi della richiesta macchina (memoria e tempo di
esecuzione).
17

Formulazione dell’elemento finito tridimensionale Cap. 2
La matrice di rigidezza dell’elemento finito solido in questione possiede infatti 24 x 24 = 576
elementi, contro (2 x 4) x (2 x 4) = 64 del corrispondente elemento piano (Isop4).
Ad ogni nodo le incognite sono costituite dagli spostamenti nelle tre direzioni cartesiane X, Y, Z
visibili in figura 2.1. I parametri nodali che definiscono lo spostamento in una di queste direzioni
sono in numero di 8 (uno spostamento per nodo), dato che lo spostamento in una direzione, risulta
indipendente dagli spostamenti nelle altre 2 direzioni, il polinomio interpolante deve contenere 8
termini del triangolo di Pascal. I primi 7 sono facilmente individuabili e sono 1 (il termine costante),
x, y, z, xy, yz, zx. Il settimo deve essere scelto tra i polinomi di grado cubico, dovendo rispettare la
simmetria nel triangolo di Pascal (isotropia geometrica) e dovendo contenere termini lineari nelle tre
coordinate (spostamento lungo gli spigoli lineare), il solo termine adatto è xyz.
Volendo che l’elemento sia compatibile, e volendo rappresentare geometrie anche non regolari, è
richiesta una trasformazione parametrica (figura 2.1) che trasformi l’elemento reale distorto in un
elemento parente regolare di lato 2, passando dal riferimento x, y, z a quello nelle coordinate ξ, η, ρ.
Definendo la trasformazione tramite le stesse funzioni di forma utilizzate in seguito per descrivere le
incognite nodali, la trasformazione viene detta isoparamentrica. Una volta definita la trasformazione
è possibile scrivere le funzioni di forma per l’elemento regolare nelle coordinate ξ, η, ρ.
Le funzioni di forma di questo elemento sono ricavabili tramite il procedimento algebrico
generalizzato: imposizione che nel nodo i lungo la direzione j l’incognita Φ valga Φ ij . Questo metodo
però, applicabile per l’elemento piano CST ed in genere a qualsiasi elemento, risulta molto laborioso
date le dimensioni delle matrici in causa. E’ preferibile utilizzare metodi meno meccanici e più
intuitivi. In questo caso, ricordandoci le proprietà di una funzione di forma descritte al punto 7 del
capitolo precedente, posso scrivere la funzione del nodo i come produttoria delle equazioni dei 3
piani che passano per tutti gli altri nodi (in questo modo sono sicuro che negli altri nodi la funzione di
forma è nulla) e poi imporre che sia unitaria nel nodo i. Così facendo si ricavano le 8 funzioni di
forma, che possono essere scritte in forma compatta [L1, L3, L5, L7, L8]:
N
i
1
= ⋅
i
i
1
8
( 1+
ξ ⋅ξ
) ⋅ ( 1+
η ⋅η
) ⋅ ( + ρ ⋅ ρ )
i
(2.1)
dove ξ i , η i , ρ i sono le coordinate del generico nodo i (o +1 o –1).
18

Formulazione dell’elemento finito tridimensionale Cap. 2
Organizzando il vettore delle incognite secondo il seguente schema:
Nodo 1 1, 2, 3. (u, v, w – spostamento in x, y, z)
Nodo 2 4, 5, 6.
…
…
Nodo 8 22, 23, 24
Si nota la relazione, che tornerà utile in fase di programmazione, tra i gradi di libertà associati ad un
nodo, ed il numero del nodo stesso:
Gdl associato all’incognita u nel nodo nnodo = nnodo ⋅3 − 2
Gdl associato all’incognita v nel nodo nnodo = nnodo ⋅3 −1
Gdl associato all’incognita w nel nodo nnodo = nnodo ⋅3
Il vettore delle funzioni di spostamento s (3x1) e quello delle incognite nodali q (24x1) sono i
seguenti:
⎡u(
x,
y,
z)
⎤
s =
⎢ ⎥
⎢
v(
x,
y,
z)
⎥
⎢⎣
w(
x,
y,
z)
⎥⎦
⎡ u1
⎤
⎢ ⎥
⎢
v1
⎥
⎢w
⎥
1
⎢ ⎥
⎢u2
⎥
⎢v
⎥
2
⎢ ⎥
q = ⎢w2
⎥
(2.2)
⎢ . ⎥
⎢ ⎥
⎢ . ⎥
⎢
u
⎥
⎢
8
⎥
⎢ v8
⎥
⎢ ⎥
⎣w8
⎦
Le incognite nodali rappresentano i pesi per cui devono essere moltiplicate le funzioni di forma per
interpolare gli spostamenti. Avendo definito l’organizzazione del vettore q, si può ora costruire la
matrice N.
19

Formulazione dell’elemento finito tridimensionale Cap. 2
⎡N1
0 0 N
2
0 0 . . . N8
0 0 ⎤
N =
⎢
⎥
⎢
0 N1
0 0 N
2
0 . . . 0 N8
0
⎥
(2.3)
⎢⎣
0 0 N
⎥
1
0 0 N
2
. . . 0 0 N8
⎦
Questa matrice, definita nello spazio normalizzato ξ, η, ρ servirà sia per interpolare gli spostamenti
che per la trasformazione isoparametrica.
s = N ⋅ q
(2.4)
X = N ⋅ Ε
(2.5)
Essendo X il vettore delle coordinate x, y, z e E quello delle coordinate ξ, η, ρ. Per le proprietà delle
funzioni di forma, si nota immediatamente che al nodo i dell’elemento parente nello spazio
normalizzato corrisponde, tramite la relazione (2.5), il nodo i dell’elemento reale. La trasformazione
sarà biunivoca se l’elemento reale non è troppo distorto, ovvero se il determinante Jacobiano della
trasformazione risulta diverso da zero. Come si sono riportati i nodi dell’elemento dallo spazio
normalizzato a quello reale, si possono riportare anche gli assi ξ, η, ρ. Si nota che le coordinate
cartesiane ξ, η, ρ dello spazio normalizzato, si trasformano in coordinate curvilinee nello spazio
reale.
Dobbiamo ora definire le deformazioni. In uno stato di sforzo 3D le deformazioni da tenere in conto
sono tutte e 6.
ε
x
∂u
=
∂x
γ
xy
∂u
∂v
= +
∂y
∂x
∂v
ε
y
=
∂y
∂v
∂w
γ
yz
= +
(2.6)
∂z
∂y
ε
z
∂w
=
∂z
γ
zx
∂w
∂u
= +
∂x
∂z
20

Formulazione dell’elemento finito tridimensionale Cap. 2
Organizzando il vettore delle funzioni di deformazione come:
⎡ ε
x ⎤
⎢ ⎥
⎢
ε
y
⎥
⎢ ε ⎥
z
ε = ⎢ ⎥
(2.7)
⎢γ
xy ⎥
⎢γ
⎥
yz
⎢ ⎥
⎢⎣
γ
zx ⎥⎦
Si può ricavare l’operatore di congruenza che agendo sul vettore degli spostamenti s fornisce il
vettore delle deformazioni ε secondo la relazione (1.10) :
⎡∂
⎢ ∂x
⎢ 0
⎢
⎢ 0
L = ⎢
⎢
∂
∂y
⎢
⎢ 0
⎢
⎢
∂
⎣ ∂z
0
∂
∂y
0
∂
∂x
∂
∂z
0
0 ⎤
⎥
0 ⎥
⎥
∂ ⎥
∂z
⎥
0 ⎥
⎥
∂
∂y⎥
⎥
∂
∂x⎥⎦
(2.8)
Facendo operare L sulla matrice N si ricava la matrice di congruenza interna dell’elemento finito B:
⎡∂N
⎢
⎢
∂x
⎢ 0
⎢
⎢
⎢ 0
B = ⎢
⎢∂N
⎢ ∂y
⎢
⎢ 0
⎢
⎢∂N
⎢
⎣ ∂z
1
1
1
0
∂N
∂y
0
∂N
∂x
∂N
∂z
0
1
1
1
0
0
∂N
∂z
0
1
∂N
∂y
∂N
∂x
1
1
∂N
∂x
0
0
∂N
∂y
0
2
2
∂N
∂z
2
0
∂N
∂y
0
∂N
∂x
∂N
∂z
0
2
2
2
0
0
∂N
∂z
0
2
∂N
∂y
∂N
∂x
2
2
...
...
...
...
∂N
∂x
0
0
...
∂N
∂y
0
∂N
8
8
8
∂z
0
∂N
∂y
0
∂N
8
8
∂x
∂N
8
∂z
0
0
0
∂N
∂z
0
∂N
8
8
∂y
∂N
8
∂x
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(2.9)
21

Formulazione dell’elemento finito tridimensionale Cap. 2
Si nota che volendosi 6 deformazioni la matrice B possiede 6 righe ed avendosi 8 nodi con 3
incognite per nodo, la matrice B possiede 3 x 8 = 24 colonne. Le funzioni N i sono definite nelle
coordinate ξ, η, ρ dello spazio normalizzato, per cui le derivate che contiene la matrice B sono
derivate di funzioni composte:
∂N
i
∂x
∂N
i ∂ξ
∂N
i ∂η
∂N
i ∂ρ
= + +
∂ξ
∂x
∂η
∂x
∂ρ
∂x
(2.10)
La trasformazione che permette di relazionare lo spazio reale con quello normalizzato, è scritta come
X = X(ξ, η, ρ), la trasformazione inversa non è nota. Si preferisce quindi sviluppare le derivate nella
forma:
∂N
i
∂N
i ∂x
∂N
i ∂y
∂N
i ∂y
= + +
(2.11)
∂ξ
∂x
∂ξ
∂y
∂ξ
∂y
∂ξ
In questo modo è possibile ricavare le derivate cercate risolvendo 8 sistemi lineari, uno per ogni
funzione di forma:
⎡∂N
i
⎤ ⎡ ∂x
⎢ ⎥ ⎢
⎢
∂ξ
⎥ ⎢
∂ξ
⎢∂N
i ⎥ ⎢ ∂x
=
⎢ ∂η
⎥ ⎢∂η
⎢∂N
⎥ ⎢
i
∂x
⎢ ⎥ ⎢
⎢⎣
∂ρ
⎥⎦
⎢⎣
∂ρ
∂y
∂ξ
∂y
∂η
∂y
∂ρ
∂z
⎤ ⎡∂N
i
⎤
∂ξ
⎥ ⎢ ⎥
⎥ ⎢ ⎥
∂z
⎢
∂ ∂
⎥ N x i
⋅ ⎥
∂η
⎥ ⎢ ∂y
⎥
∂z
⎥ ⎢∂N
⎥
i
⎥ ⎢ ⎥
∂ρ
⎥⎦
⎣ ∂z
⎦
(2.12)
Il vettore dei termini noti viene valutato come:
⎡∂N
i
⎤ ⎡1
⎤
⎢ ⎥ ⎢ ξ + +
⎥
⎢
∂
i
(1 ηηi
)(1 ρρ )
ξ
i
⎥ 8
⎢
⎥
⎢∂N
i ⎥ 1
= ⎢ ηi
(1 + ξξ
i
)(1 + ρρi
) ⎥
⎢ ∂η
⎥ ⎢8
⎥
⎢∂N
⎥ ⎢1
i
⎥
⎢ ⎥ ⎢
ρi
(1 + ξξ
i
)(1 + ηηi
)
⎣
⎥
⎢⎣
∂ρ
⎥⎦
8
⎦
(2.13)
22

Formulazione dell’elemento finito tridimensionale Cap. 2
La matrice dei coefficienti è detta matrice Jacobiana (J) e dipende solamente dalla trasformazione:
J
⎡ ∂x
⎢
⎢
∂ξ
⎢
⎢ ∂x
= ⎢
⎢∂η
⎢
⎢ ∂x
⎢
⎢⎣
∂ρ
∂y
∂ξ
∂y
∂η
∂y
∂ρ
∂z
⎤ ⎡
∂ξ
⎥ ⎢
⎥ ⎢
⎥ ⎢
∂z
⎥ ⎢
⎥ ⋅ ⎢
∂η
⎥ ⎢
⎥ ⎢
∂z
⎥ ⎢
⎥ ⎢
∂ρ
⎥⎦
⎢⎣
8
∑
i=
1
8
∑
i=
1
8
∑
i=
1
∂N
i
x
∂ξ
i
∂N
i
x
∂η
i
∂N
i
x
∂ρ
i
8
∑
i=
1
8
∑
i=
1
8
∑
i=
1
∂N
i
y
∂ξ
i
∂N
i
y
∂η
i
∂N
i
y
∂ρ
i
8
∑
i=
1
8
∑
i=
1
8
∑
i=
1
∂N
i
⎤
zi
∂ξ
⎥
⎥
⎥
∂N
⎥
i
zi
⎥
∂η
⎥
⎥
∂N
⎥
i
zi
⎥
∂ρ
⎥⎦
(2.14)
Si nota che se la trasformazione è solamente un cambio di scala, la matrice Jacobiana diventa:
J
⎡a
=
⎢
⎢
0
⎢⎣
0
0
b
0
0⎤
0
⎥
⎥
c⎥⎦
(2.15)
Se l’elemento è distorto, sarà in generale una matrice piena. Per non avere fenomeni di ripiegamento
durante la trasformazione (perdita di biunivocità), viene richiesto che il determinante della matrice J
sia strettamente maggiore di zero. Ricavata la matrice B si deve ora formare la matrice di rigidezza K
dell’elemento finito, dalla relazione (1.18) si ha:
K = B D B dV
e ∫ ⋅ ⋅
(2.16)
Ve
T
Dove la matrice D è la matrice delle costanti elastiche del materiale:
⎡1
⎢
⎢
B
⎢B
D = A⋅
⎢
⎢0
⎢0
⎢
⎣0
B
1
B
0
0
0
B
B
1
0
0
0
0
0
0
C
0
0
0
0
0
0
C
0
0 ⎤
0
⎥
⎥
0 ⎥
⎥
0 ⎥
0 ⎥
⎥
C
⎦
(2.17)
23

Formulazione dell’elemento finito tridimensionale Cap. 2
E(1
−υ)
A =
(1 + υ)(1
− 2υ
)
υ
B =
( 1−υ)
1−
2υ
C =
(2.18)
2(1 −υ)
La matrice (2.17) e le costanti (2.18) sono valide in caso di elasticità lineare e di materiali isotropo (2
costanti elastiche, E e ν). Se il materiale non fosse lineare, sarebbe necessario l’introduzione di una
legge costitutiva che modelli le rigidezze del materiale a seconda dello stato di sforzo. Se il materiale
fosse non isotropo, la matrice D conterrebbe più costanti elastiche e sarebbe scritta secondo un ben
preciso sistema di assi di riferimento locale, si renderebbe quindi necessaria una rotazione degli assi
dal sistema locale al sistema globale.
La matrice B contiene però delle funzioni di ξ, η, ρ, per cui l’integrale va fatto con le coordinate del
dominio normalizzato che rappresentano, come già detto, un sistema di coordinate curvilineo per
l’elemento reale. L’elemento di volume infinitesimo può essere definito come:
dV
= ( dξ
∧ dη)
⋅ d ρ
(2.19)
I versori del sistema di coordinate curvilinee può essere scritto riferendosi alla terna cartesiana,
tramite gli incrementi delle funzioni x, y, z nelle direzioni dei tre versori:
∂x
∂y
∂z
dξ
= dξ
⋅ i + dξ
⋅ j + dξ
⋅ k
∂ξ
∂ξ
∂ξ
∂x
∂y
∂z
dη
= dη
⋅i
+ dη
⋅ j + dη
⋅ k
∂η
∂η
∂η
(2.20)
∂x
∂y
∂z
dρ
= dρ
⋅i
+ dρ
⋅ j + dρ
⋅ k
∂ρ
∂ρ
∂ρ
24

Formulazione dell’elemento finito tridimensionale Cap. 2
L’elemento infinitesimo di volume è:
dV
⎡ ∂x
∂y
∂z
⎤ ⎡ ∂x
∂y
∂z
⎤
⎢ dξ
dξ
dξ
ξ ξ ξ
⎥ ⎢
ξ ξ ξ
⎥
⎢
∂ ∂ ∂
⎥ ⎢
∂ ∂ ∂
⎥
⎢
⎥ ⎢
⎥
⎢ ∂x
∂y
∂z
⎥ ⎢ ∂x
∂y
∂z
⎥
= det ⎢ dη
dη
dη⎥
= det⎢
⎥ ⋅ dξ
⋅ dη
⋅ dρ
= det[ J ] ⋅ dξ
⋅ dη
⋅ dρ
(2.21)
⎢∂η
∂η
∂η
⎥ ⎢∂η
∂η
∂η
⎥
⎢
⎥ ⎢
⎥
⎢ ∂x
∂y
∂z
⎥ ⎢ ∂x
∂y
∂z
⎥
⎢ dρ
dρ
dρ
⎥ ⎢
⎥
⎢⎣
∂ρ
∂ρ
∂ρ
⎥⎦
⎢⎣
∂ρ
∂ρ
∂ρ
⎥⎦
Infatti sia B la matrice ottenuta dalla matrice A, moltiplicandone una riga per uno scalare k, il
determinate di B risulta: det( B)
= k ⋅ det( A)
. Sfruttando questa proprietà si è potuto raccogliere dξ,
dη,dρ all’esterno della matrice, e mettere in mostra il determinante della matrice Jacobiana.
La relazione (2.16) si può quindi scrivere come:
K
e
=
1 1 1
∫ ∫ ∫
−1
−1
−1
B
T
⋅ D ⋅ B ⋅ det( J ) ⋅ dξ
⋅ dη
⋅ dρ
(2.22)
Essendo, in generale, il determinante Jacobiano una funzione razionale, l’integrale si esegue per via
numerica utilizzando le formule di Gauss.
K
e
n
n
n
= ∑∑∑
i= 1 j= 1 k = 1
T
[ B ⋅ D ⋅ B ⋅ J )] ⋅Wi
⋅W
j
⋅Wk
det( (2.23)
ijk
La quantità tra parentesi quadra va calcolata in ogni punto di Gauss, moltiplicato al peso della
formula e poi sommata a quelle relative agli altri punti. Se n è il numero di punti di Gauss, è noto che
l’integrale numerico è esatto per un polinomio al massimo di grado 2n – 1, per cui, essendo la matrice
B composta da termini lineari, e supponendo che il determinante di J sia una costante, si dovrà
prendere almeno un reticolo di 8 punti (n=2) all’interno dell’elemento (supponendo di utilizzare la
firmula di Gauss-Legendre).
25

Formulazione dell’elemento finito tridimensionale Cap. 2
Si è visto che se l’elemento non è distorto il determinante di J è effettivamente una costante (2.15) e
vale un ottavo del volume, per cui l’integrazione risulta esatta. Se l’elemento è distorto la funzione da
integrare non è più un polinomio, per cui è possibile solo approssimare il valore dell’integrale. Per la
1 1 1
formula di integrazione di Gauss-Legendre 2x2x2 i punti hanno coordinate ± ; ± ; ± e pesi
3 3 3
pari ad 1.
Le forze nodali equivalenti alle forze di volume (peso oppure inerzia) si integrano allo stesso modo
partendo dall’equazione (1.19):
F
e
n n n
T
∫ N ⋅ F ⋅ dV =
Ve
i= 1 j= 1 k=
1
= ∑∑∑
T
[ N ⋅ F ⋅ J )] ⋅Wi
⋅W
j
⋅Wk
det( (2.24)
ijk
2. La rigidezza dell’elemento compatibile
L’elemento così formulato risulta compatibile e conforme. La matrice B contiene infatti delle
derivate di ordine massimo pari a 1 (m=1), la completezza è garantita dal fatto che il polinomio
interpolante è completo sino al grado 1, la conformità perché il polinomio interpolante risulta C ∞
all’interno dell’elemento e C 0 sulla sua frontiera. E’ possibile quindi interpolare correttamente campi
di variazione lineare di spostamento senza alcun riguardo alla forma dell’elemento. Non è così se lo
spostamento da interpolare risulta quadratico (stato deformativi flessionale). Si riportano i risultati di
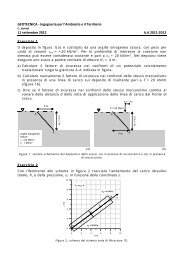
un Pacth Test [L1] eseguito sul corrispondente elemento bidimensionale (Isop4).
4
y
3
1
x
2
2
2a
Figura 2.2: Elemento Isop4.
Imponendo il campo di spostamento quadratico:
26

Formulazione dell’elemento finito tridimensionale Cap. 2
u = xy
1 v = − x
2
2
La soluzione esatta fornisce deformazioni e sforzi nulli, la soluzione approssimata con l’elemento:
γ = xy
x
Ex
τ
xy
=
2(1
+ υ)
L’elemento non riesce a riprodurre lo stato di deformazione imposto. Il valore non corretto dello
scorrimento si ripercuote sull’energia di deformazione a taglio, teoricamente nulla:
2Ea
2Ea
=
⎛ 1−υ
2 ⎞
esatta 2
U totale
approssimata
= ⎜1+
a
2
⎟
3(1 −υ )
3(1 −υ
) ⎝ 2 ⎠
U totale
2
L’energia di deformazione tende ad amplificarsi tramite il rapporto ( 1 (1 −υ)
a 2)
+ , fattore che
tende a crescere con l’aumentare della snellezza dell’elemento. L’eccessivo valore di U comporta un
elevato valore della rigidezza, fenomeno chiamato Shear Locking. Questo comportamento è esaltato
negli elementi semplici, in cui le funzioni di forma sono rappresentate da polinomi di gradi basso.
L’elemento solido ha un comportamento analogo, con Locking nelle tre componenti di taglio.
Per rimediare a questo inconveniente si possono seguire diverse alternative, in questo lavoro si è
esaminata l’integrazione selettiva e l’aggiunta di funzioni di forma incompatibili.
3. L’integrazione selettiva
Dal paragrafo precedente si nota che la distribuzioni dello scorrimento γ xy = x permette di rimediare
all’inconveniente del Locking calcolando l’energia a taglio in x = y = 0. Ragionamento analogo per
l’elemento solido. Calcolando l’energia di deformazione a taglio nell’unico punto di Gauss x = y = z
= 0 la si pone numericamente a zero. Si tratta quindi di integrare la matrice di rigidezza con una
integrazione 2x2x2 per le deformazioni normali e con una integrazione ridotta per lo scorrimento
[L1, L4, L5, L9, L16].
27

Formulazione dell’elemento finito tridimensionale Cap. 2
Si partiziona la matrice del materiale D nel modo seguente:
⎡D
n
D = ⎢
⎣
0
0 ⎤
D
⎥
t ⎦
(2.25)
D n
⎡1
= A⋅
⎢
⎢
B
⎢⎣
B
B
1
B
B⎤
B
⎥
⎥
1⎥⎦
⎡C
0
D = ⋅
⎢
t
A
⎢
0 C
⎢⎣
0 0
0 ⎤
0
⎥ ⎥⎥ C⎦
Con A, B, C, si sono indicati gli stessi parametri in (2.18). La matrice D n raccoglie le caratteristiche
del materiale relative ai fenomeni normali, la D t ai fenomeni taglianti.
Allo stesso modo si può partizionare la matrice B:
⎡B
⎤
n
B = ⎢ ⎥
(2.26)
⎣
B
t ⎦
⎡∂N1
⎢
⎢ ∂x
= ⎢ 0
⎢
⎢
⎢ 0
⎣
0
∂N
∂y
∂N
∂z
∂N
∂x
2
∂N
∂y
∂N
∂z
∂N
∂x
∂N
∂y
1
2
8
B n
0 0
0 ... ... ... ... ... 0 0
1
2
8
0
0
0
0
0
0
0
8
0
0
0
∂N
∂z
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎡∂N
⎢
⎢
∂y
= ⎢ 0
⎢
⎢∂N
⎢
⎢⎣
∂z
1
∂N
∂x
∂N
∂z
1
∂N
∂y
∂N
∂x
∂N
∂y
2
∂N
∂z
∂N
∂x
∂N
∂z
2
∂N
∂y
∂N
∂x
∂N
∂y
∂N
∂z
∂N
∂x
∂N
∂z
⎤
0 ⎥
⎥
∂N
8 ⎥
∂y
⎥
∂N
⎥
⎥
∂x
⎥⎦
1 1
2 2
8
B t
0
... ... ... ... ... 0
1
1 2
2
8
8
0
0
0
0
8
0
8
28

Formulazione dell’elemento finito tridimensionale Cap. 2
In questo modo, operando le operazioni matriciali per blocchi, si giunge alla seguente formulazione
della matrice di rigidezza dell’elemento finito:
∫
∫
K = B ⋅ D ⋅ B ⋅ dV + B ⋅ D ⋅ B ⋅ dV
(2.27)
e
Ve
n
T
n
n
Ve
t
T
t
t
Da notare che la matrice K e rimane sempre una 24x24, dato che i prodotti matriciali forniscono
(24x3)x(3x3)x(3x24) = (24x24). Ora però il contributo tagliante è separato dal contributo normale,
per cui si può integrare con una integrazione selettiva (diversa per i due contributi):
2
2
2
∑∑∑
i= 1 j= 1 k = 1
1 1 1
T
T
[ B ⋅D
⋅B
⋅det(
J )] + [ B ⋅D
⋅B
⋅det(
J )]
∑∑∑
K =
⋅8
(2.28)
e
n
n
n
ijk
i= 1 j = 1 k = 1
t
t
t
ijk
dove si sono già inseriti i pesi delle formule di Gauss – Legendre, pensando ad integrazioni su 2x2x2
punti e su 1 punto.
L’integrazione selettiva su elementi Isop4 piani da risultati ottimi. Nel caso si usi su un elemento
esaedrico nasce però un problema. Se la matrice dell’elemento Isop4 venisse integrata utilizzando
un’integrazione ridotta, anziché selettiva si vedrebbe la nascita di due modi ad energia nulla, detti
modi spuri, questo comporta l’introduzione di labilità non volute nel modello strutturale, e bisogna
prestare molta attenzione al fatto che un modo spurio non possa propagarsi [L1, L4].
4
y
3
x
1
2
Figura 2.3: Esempio di un modo spurio.
Il modo deformativi ad energia nulla nasce perché si valuta l’energia di deformazione nell’unico
punto x = y = 0, dove il contributo tagliante è nullo per una deformazione imposta come in figura 2.3
29

Formulazione dell’elemento finito tridimensionale Cap. 2
(di tipo flessionale), ma è nullo anche il contributo dovuto alle deformazioni normali, in quanto
l’elementino infinitesimo posto nell’origine degli assi non si deforma. L’integrazione selettiva
scavalca questo problema, valutando il contributo flessionale in altri punti.
Esaminiamo però il caso di un elemento solido esaedrico sottoposto ad integrazione selettiva. Diamo
una deformata all’elemento di tipo torsionale attorno ad uno dei tre assi. Il contributo all’energia
deformativi dovuto alla deformazione tagliante è nulla, in quanto viene calcolata nell’unico punto x =
y = z = 0. Il contributo dovuto alle deformazioni normali si calcola nei punti di gauss 2x2x2.
Supponiamo che la torsione avvenga attorno all’asse x. I piani perpendicolari all’asse x rimangono
piani a deformazione avvenuta (l’elemento non è in grado di cogliere l’ingobbimento della sua
sezione) per cui la deformazione ε x è nulla in tutti e 8 i punti di Gauss. Ma anche le deformazioni ε y e
ε z sono nulle in quanto nel piano xz la sezione ha un moto di rotazione e non si deforma.
4
z
3
x
1
2
Figura 2.4: Stato deformativo in una sezione perpendicolare all'asse di torsione.
L’energia di deformazione risulta quindi nulla. Anche se opero con l’integrazione selettiva, esistono
3 modi spuri (una torsione attorno a ciascun asse) che rendono labile il sistema.
Una prova numerica di quanto esposto è ottenibile dal caso seguente. Si vuole simulare una prova di
trazione lungo l’asse x su di un singolo elemento esaedrico regolare di lato 2 con baricentro
nell’origine degli assi, utilizzando l’integrazione selettiva. Si è scelto di porre 0 il coefficiente di
Poisson, in questo modo, vincolando tutti gli spostamenti dei quattro nodi a quota x = -1, e
sottoponendo i nodi a quota x = 1 ad una forza parallela all’asse x, l’unico spostamento che ci si
aspetta è in direzione x, peraltro facilmente calcolabile.
La simulazione numerica si blocca all’atto della risoluzione del sistema, con l’avviso: termine
pivotale nullo, sistema labile.
30

Formulazione dell’elemento finito tridimensionale Cap. 2
z
y
F
F
x
F
F
Figura 2.5: Elemento in trazione.
Ricopiando la matrice dei coefficienti in un programma di analisi matematica è possibile calcolarne
autovalori e autovettori. Ci si può così accorgere che la matrice della rigidezza (a cui sono già state
tolte le righe e le colonne relative ai vincoli) risulta labile. Infatti un autovalore risulta nullo, ed il
corrispondente autovettore ha forma:
Nodo 5 Nodo 6 Nodo 7 Nodo 8
u i (in dir. x) 0 0 0 0
v i (in dir. x) -K -K K K
w i (in dir. x) +K -K -K K
Dove K è una costante generica. Si può notare che si sviluppa un modo ad energia nulla.
Se si aggiunge un vincolo, atto a bloccare la nascita di questo modo deformativo:
z
y
F
F
x
F
Biella
F
Figura 2.6: Elemento in trazione con un vincolo aggiuntivo.
I risultati che si ottengono sono corretti, ed il vincolo aggiuntivo ha reazione vincolare nulla.
31

Formulazione dell’elemento finito tridimensionale Cap. 2
4. Le funzioni di forma incompatibili
Un approccio basato sull’integrazione selettiva, produce per l’elemento esaedrico a 8 nodi, la nascita
di tre modi spuri di forma torsionale. Un secondo metodo per eliminare lo shear locking introdotto da
Wilson consiste nell’introduzione di ulteriori funzioni di forma legati a dei parametri incogniti α
interni all’elemento che descrivano dei modi di deformazione quadratica. Un elemento così formulato
riproduce correttamente un campo di sforzi flessionale senza introdurre modi spuri [L1, L5, L9, L16,
L17], [Wil], [Tay], [Les].
4 3
4
3
4 3
1
2
1
2
1
2
Figura 2.7: Aggiunta della funzione di forma incompatibile.
Nel caso tridimensionale le funzioni incompatibili da aggiungere sono:
2
ψ
1
= 1−ξ
2
ψ
2
= 1−η
2
= −
(2.29)
ψ
3
1 ρ
Il vettore q contiene ora anche 9 incognite interne, ha quindi dimensioni 33x1. La matrice N è
⎡N1
0 0 N
2
0 0 . . . ψ
3
0 0 ⎤
N =
⎢
⎥
⎢
0 N1
0 0 N
2
0 . . . 0 ψ
3
0
⎥
(2.30)
⎢⎣
0 0 N
⎥
1
0 0 N
2
. . . 0 0 ψ
3 ⎦
e ha dimensioni 3x33. Lo sviluppo segue le stesse regole dell’elemento compatibile, nella
trasformazione parametrica non compaiono le funzioni di forma incompatibili, per cui l’elemento è
del tipo super parametrico (si utilizzano meno funzioni per descrivere la geometria rispetto a quelle
utilizzate per descrivere gli spostamenti).
32

Formulazione dell’elemento finito tridimensionale Cap. 2
I gradi di libertà introdotti con le funzioni incompatibili, sono scomodi da trattare in un codice di
calcolo, perché non sono associate a nessun nodo visibile. E’ possibile condensarli staticamente in
modo da ottenere una matrice di rigidezza sempre di 24x24.
Ottenuta la matrice 33x33, si partizioni il sistema relativo al singolo elemento come segue:
⎡K
K ⎤ ⎡q⎤
⎡F
cc cn
q ⎤
⎢ ⎥ ⋅ ⎢ ⎥ + ⎢ ⎥ = 0
(2.31)
⎣
K K
⎦ ⎣α ⎦ ⎣F nc nn
α ⎦
Si ricava il vettore a dalla seconda equazione e lo si sostituisce nella prima:
−1
α = K ( −F
− K q)
(2.32)
nn
α
nc
cond
cond
K ⋅ q + F = 0
(2.33)
Dove si è posto:
K
cond
−1
= K − K K K
F
cond −
F K K F
cc cn nn nc
q
−
1
cn nn α
= (2.34)
In questo modo la matrice di rigidezza dell’elemento ed il vettore delle forze hanno ancora
dimensioni 24x24 e 24x1.
33

Formulazione dell’elemento finito tridimensionale Cap. 2
5. I vincoli elastici concentrati
Si introduce ora la rigidezza di una molla elastica vincolante un nodo qualsiasi. L’orientamento della
molla nello spazio è dato dai tre coseni direttori dell’asse della molla θ x , θ y , θ z . Siano q x , q y , q z gli
spostamenti di un estremo della molla, l’allungamento si può scrivere come:
∆ = q cos( θ ) + q cos( θ ) + q cos( θ )
(2.35)
x
x
y
y
z
z
L’energia di deformazione risulta:
U
=
1
2
k
[ q cos( θ ) + q cos( θ ) + q cos( θ )] 2
x
x
y
y
z
z
U
1 2
2
2 2
2
2
= k[
q
x
cos ( θ
x
) + q
y
cos ( θ
y
) + q
z
cos ( θ
z
) +
2
2q
q cos( θ )cos( θ ) + 2q
q cos( θ ) cos( θ ) + 2q
q
x
y
x
y
y
z
y
z
x
z
cos( θ ) cos( θ )]
x
z
Raccogliendo si ottiene:
U
1
=
2
[ q q q ]
x
y
z
2
⎡ cos ( θ
x
)
⎢
⋅ k⎢cos(
θ
y
)cos( θ
x
)
⎢
⎣
cos( θ
z
)cos( θ
x
)
cos( θ )cos( θ )
x
2
cos ( θ )
cos( θ )cos( θ )
z
y
y
y
cos( θ ⎤
x
)cos( θ
z
) ⎡q
⎥
cos( θ ⋅
⎢
y
)cos( θ
z
) ⎥ ⎢
q
2
cos ( θ ⎥
⎦
⎢
z
) ⎣q
x
y
z
⎤
⎥
⎥
⎥⎦
(2.36)
Il termine raccolto tra i due vettori di spostamento rappresenta la matrice di rigidezza della molla, e
andrà assemblata ai termini della matrice di rigidezza totale corrispondenti ai gradi di libertà vincolati
dalla molla.
34

Formulazione dell’elemento finito tridimensionale Cap. 2
6. Deformazioni anelastiche
Se sono presenti delle deformazioni anelastiche ε i (ritiro, temperatura…), le tensioni si scrivono:
σ = D ⋅ ε − ε )
(2.37)
(
i
per cui il lavoro interno scritto al punto (1.15) assume ora la forma più generale:
∫
∫
L = δ ε ⋅σ
⋅ dV = δ ε ⋅ D ⋅ ( ε − ε ) ⋅ dV
(2.38)
i
Ve
T
Ve
T
i
Dalla (2.38) svolgendo il prodotto e separando i due integrali si nota che alla variazione di energia di
deformazione calcolata con le deformazioni totali, viene sottratta la parte dovuta alle deformazioni
anelastiche. Essendo note, questo termine viene portato a destra dell’uguale nell’equazione (1.5), e
determina il contributo al vettore dei carichi nodali dato dalle deformazioni anelastiche.
∫
F = B ⋅ D ⋅ε ⋅ dV
(2.39)
i
V
t
i
Il vettore (2.39) è relativo ad un solo elemento, per cui è da utilizzare in fase di assemblaggio del
vettore totale dei carichi nodali equivalenti.
E’ da ricordare poi che se sono presenti delle deformazioni anelastiche, le tensioni, dopo avere
assemblato e risolto il sistema, vanno sempre calcolate utilizzando la (2.37).
35

Formulazione dell’elemento finito tridimensionale Cap. 2
7. Armatura embedded
Vi sono diversi metodi per modellare l’armatura presente nel calcestruzzo in un codice di calcolo
numerico. Un modo particolarmente efficace, consiste nel trattare la barra di armatura come se fosse
un corpo (avente caratteristiche meccaniche proprie) immerso nell’elemento finito. L’apporto di
rigidezza alla matrice
K dell’elemento può essere calcolato come segue (la formulazione viene
e
eseguita per l’elemento incompatibile, per quello compatibile è analoga) [Kwa].
B
z
A
y
x
Figura 2.8: Elemento embedded all'interno di un elemento finito.
Siano A e B i punti di frontiera della barra di armatura per l’elemento considerato, sia L la lunghezza
del tratto di armatura presente nell’elemento, la deformazione della barra, intesa come biella, vale:
sa
− sb
ε
b
=
(2.40)
L
dove con s a e s b si sono indicati gli spostamenti dei punti di frontiera in direzione della barra (sono
scalari). La direzione della barra viene definita tramite i coseni direttori della retta che parte dal punto
A e passa per il punto B. Gli spostamenti lungo la barra valgono:
s
s
a
b
= q cos( θ ) + q cos( θ ) + q cos( θ ) = T ⋅ q
xa
xb
x
x
ya
yb
y
y
za
zb
z
z
a
= q cos( θ ) + q cos( θ ) + q cos( θ ) = T ⋅ q
(2.41)
b
36

Formulazione dell’elemento finito tridimensionale Cap. 2
dove T è il vettore riga 1x3 che contiene i coseni direttori, e q i è il vettore colonna 3x1 che contiene
gli spostamenti del generico punto i (in generale non coincidente con un nodo). É possibile valutare
gli spostamenti dei punti A e B tramite l’interpolazione degli spostamenti nodali eseguita con le
funzioni di forma:
s
a
= T ⋅ q
a
= T ⋅ N
A
⋅ q
s
b
= T ⋅ q = T ⋅ N ⋅ q
(2.42)
b
B
Dove il vettore q 33x1 racchiude tutti gli spostamenti dei nodi e le matrici delle funzioni di forma
sono valutate nei punti A e B. La deformazione assiale della barra di armatura risulta:
ε
b
=
1
( T ⋅ N ⋅ q − T ⋅ N ⋅ q) ⋅ = T ⋅ ( N − N )
A
B
L
A
B
1
⋅ q ⋅
L
( N − N )
1
δε
b
= T ⋅ ⋅δ
q ⋅
(2.43)
A B
L
La tensione nella barra, tenendo conto anche di deformazioni anelastiche in modo da poter modellare
anche le armature di precompressione, è la stessa del (2.37) scritta come legame uniassiale:
σ
b
= E ⋅ ε
b
− ε
b
)
(
i
La variazione dell’energia di deformazione della barra risulta:
δ U
δU
=
∫
V
δε ⋅σ
⋅ dV
b
b
T
T ⎡
1 ⎤
( N − N ) ⋅T
⋅ E ⋅ T ⋅ ( N − N ) ⋅ q ⋅ −
bi
dV
T 1
= ∫δ
q ⋅ ⋅
L
A B ⎢
ε
A B
⎣
L ⎥
⎦
⋅
V
(2.44)
Ipotizzando di valutare E nel baricentro della barra, l’integrale contiene solo delle costanti.
37

Formulazione dell’elemento finito tridimensionale Cap. 2
Sviluppando le parentesi è possibile identificare due termini, il primo è una una matrice di rigidezza
33x33, che rappresenta l’aumento di rigidezza dell’elemento finito dovuto alla barra embedded:
K
b
T T
( N − N ) ⋅T
⋅T
⋅ ( N − N )
A ⋅ Ec
= ⋅
(2.45)
A B
A B
L
da notare che il prodotto delle due matrici T risulta pari alla matrice (2.36) utilizzata per i vincoli
elastici:
~
T = T
T
⋅T
2
⎡ cos ( θ
x
)
⎢
= ⎢cos(
θ
y
)cos( θ
x
)
⎢
⎣
cos( θ
z
)cos( θ
x
)
cos( θ )cos( θ )
x
2
cos ( θ )
cos( θ )cos( θ )
z
y
y
y
cos( θ ⎤
x
)cos( θ
z
)
⎥
cos( θ
y
)cos( θ
z
) ⎥
2
cos ( θ ) ⎥
z ⎦
(2.46)
Il secondo termine che deriva dalla (2.44) è il vettore delle forze nodali equivalenti alla
precompressione:
F
p
c
T T
( N − N ) ⋅T
⋅ε
bi
= A⋅
E ⋅
(2.47)
A
B
T T
T T
Si nota che i prodotti matriciali ( N − N ) ⋅T
⋅T
⋅ ( N − N ) e ( N N ) ⋅T
⋅ε
bi
A
B
A
B
A
− forniscono
delle costanti, perciò non è necessaria la loro valutazione ad ogni passo di carico in caso di
comportamento non lineare del materiale.
La difficoltà è ora nel valutare le matrici delle funzioni di forma nei punti A e B, in coordinate
naturali. I punti A e B sono noti infatti in coordinate cartesiane, e la trasformazione che porta le
coordinate nel sistema naturale è nota solamente se l’esaedro non è distorto:
B
ξ = ( x − xc ) / a η = ( y − yc ) / b ρ = ( z − zc ) / c
(2.48)
dove il punto c è il baricentro dell’elemento, ed a, b, c sono i suoi semilati. In caso contrario è
necessario il calcolo delle coordinate nel sistema naturale tramite iterazione.
38

Formulazione dell’elemento finito tridimensionale Cap. 2
Il metodo più semplice è quello di eseguire l’algoritmo della bisezione una volta per ogni coordinata.
Ovvero applicare 3 volte un metodo con una velocità di convergenza lineare. Molto più veloce è
l’algoritmo tangente di Newton, velocità di convergenza quadratica.
L’incremento di coordinata x si può scrivere come:
dx dx dx
dx = dξ
+ dη
+ dρ
dξ
dη
dρ
quindi:
⎡ ∂x
⎢
⎡dx⎤
⎢
∂ξ
⎢ ⎥ ⎢ ∂y
⎢
dy
⎥
=
⎢∂ξ
⎢⎣
dz⎥⎦
⎢ ∂z
⎢
⎢⎣
∂ξ
∂x
∂η
∂y
∂η
∂z
∂η
∂x
⎤
∂ρ
⎥
⎥ ⎡dξ
⎤
∂y
⎥ ⋅
⎢ ⎥
⎢
dη
⎥
= J
∂ρ
⎥
∂z
⎥ ⎢⎣
dρ⎥⎦
⎥
∂ρ
⎥⎦
T
⎡dξ
⎤
⋅
⎢ ⎥
⎢
dη
⎥
⎢⎣
dρ⎥⎦
⎡dξ
⎤
→
⎢
dη
⎥
= [ J ]
⎢ ⎥
⎢⎣
dρ⎥⎦
T −1
⎡dx⎤
⋅
⎢ ⎥
⎢
dy
⎥
⎢⎣
dz⎥⎦
(2.49)
8. Armatura diffusa
L’armatura modellata in modo embedded, è una buona approssimazione della situazione fisica della
struttura, e risulta efficiente quando le armature risultano concentrate in alcune zone (armatura
longitudinale delle travi, cavi di precompressione…). Se però l’armatura risulta distribuita (armatura
a taglio delle travi, reti di armatura…) può essere utile poterla trattare come se fosse omogeneamente
distribuita all’interno dell’elemento finito [BMR2]. In questo caso è sufficiente sommare alla matrice
D del calcestruzzo la matrice
c
sistema di riferimento globale.
D dell’armatura omogeneizzata e opportunamente ruotata nel
s
s
T
D = T
s
'
⋅D
⋅T
s
s
(2.50)
39

Formulazione dell’elemento finito tridimensionale Cap. 2
dove
'
D è la matrice 6x6 dell’armatura omogeneizzata avente come unico elemento non nullo quello
s
appartenente alla posizione (1,1) di valore sarà
ρ ⋅E
(ρ s è la percentuale di armatura presente).
s
s
Nella 2.50
T è la matrice che ruota il tensore, dal sistema di riferimento x’ - y’ - z’ solidale con
s
l’asse dell’armatura, nel sistema globale x - y - z. Se vi sono più armature, differentemente orientate,
la matrice D risulterà:
∑
D = D + T ⋅D' ⋅T
(2.51)
c
i
T
si
si
si
In questa formulazione si è assunto che il materiale fosse isotropo, se così non fosse anche le
caratteristiche meccaniche del calcestruzzo andrebbero riportate nel sistema di riferimento globale.
40

Legami costitutivi e problema non lineare Cap. 3
Capitolo 3
Legami costitutivi e problema non lineare
La non linearità si può presentare in un problema strutturale, sotto diverse forme.
• Ogni volta che un corpo subisce grandi spostamenti e/o grandi deformazioni si ha un problema di
non linearità geometrica. Per superare le difficoltà fisico-matematiche legate ha questo tipo di
problema, è necessario :
- calcolare l’equilibrio della struttura rispetto al corpo deformato
- modificare le relazioni lineari deformazione – spostamento viste nel capitolo 2 aggiungendo
anche i termini di ordine superiore.
• Un altro tipo di non linearità si manifesta quando si considerano particolari condizioni al contorno
della struttura (ad es. il contatto tra due superfici). In questo caso si parlerà di non linearità di
contorno.
• Se il materiale di cui è costituita la struttura, presenta una legge tensione – deformazione non
lineare, si ha un problema di non linearità di materiale. In questo caso, anche se le deformazioni e gli
spostamenti vengono supposti “piccoli” (in modo che sia lecito calcolare le tensioni riferendosi alla
geometria indeformata), le tensioni non sono più linearmente proporzionali alle deformazioni. Il
problema più difficile è quello di determinare una legge costitutiva per il materiale che rappresenti il
più correttamente possibile la situazione reale.
In questo lavoro si affronta il problema della non linearità di materiale, nel seguito del capitolo
verranno esposti i legami costitutivi utilizzati ed i più comuni algoritmi numerici utilizzati per la
soluzione dei sistemi di equazioni non lineari.
1. La non linearità di materiale
I materiali comunemente usati nell’ingegneria, se sottoposti ad azioni chimiche, radiazioni, carichi
meccanici o altro, possono sviluppare nel loro interno delle microfessure che ne deteriorano le
caratteristiche meccaniche. Questo fenomeno è chiamato processo di danneggiamento.
41

Legami costitutivi e problema non lineare Cap. 3
Numerosi legami costitutivi si rifanno appunto alla meccanica del danneggiamento, in questi modelli
il deterioramento del materiale è descritto tramite delle variabili interne D i (introdotte da Kachanov
nel 1958) che indicano la densità delle microfessure presenti nel materiale. Il processo di
danneggiamento può essere isotropo o anisotropo. L’assunzione dell’isotropia del materiale e del
processo di danneggiamento, è in pratica sufficiente per dare una buona stima del comportamento
generale del materiale sia sotto carico monotono sia sotto carico ciclico. L’ipotesi d’isotropia produce
inoltre notevoli semplificazioni nei calcoli, necessari per seguire l’evoluzione del danno. Nella
descrizione del comportamento di strutture in calcestruzzo armato, l’assunzione dell’isotropia di
danneggiamento comporta però notevoli errori di valutazione, in special modo per quanto riguarda la
portanza di pannelli armati soggetti a stato di sforzo di puro taglio. Per questo motivo si rende
necessaria l’introduzione di una legge costitutiva non isotropa, che tenga conto della diversità di
danneggiamento nella direzione delle trazioni rispetto a quella delle compressioni. In questo capitolo
verranno esposti il modello di danneggiamento isotropo di Mazars e di Cervera per carichi monotoni
crescenti, ed un legame costitutivo ortotropo.
2. Definizione della variabile di danno
Si consideri un solido danneggiato e se ne isoli un elemento di volume sufficientemente grande da
essere rappresentativo dello stato del materiale.
n
Figura 3.1: Volume rappresentativo.
42

Legami costitutivi e problema non lineare Cap. 3
Sia S l’area della superficie di normale n e S r l’area S depurata dai microvuoti causati dal processo di
danneggiamento (sezione reale), risulta [LeC]:
S r < S ; S d = S – S r (3.1)
Dove S d indica l’area delle microfessure presenti nella sezione considerata, mentre il danneggiamento
locale relativo alla direzione n è definito come:
Sd
Dn = (3.2)
S
D n potrà dunque assumere i seguenti valori:
D n = 0
lo stato di danno è nullo (materiale vergine)
D n = 1
l’elemento è fessurato secondo un piano di normale n
0 < D n < 1 l’elemento è danneggiato
In caso di danneggiamento isotropo il valore D n non dipende dalla normale n considerata, per cui D n è
una quantità scalare. In caso di danneggiamento anisotropo il danneggiamento è rappresentato tramite
una variabile tensoriale.
Il modello sviluppato da Mazars considera un danneggiamento isotropo, perciò è lecito porre :
D = D n (3.3)
Ciò equivale ad affermare che le microfessure causate dal danneggiamento sono orientate
uniformemente in tutte le direzioni.
43

Legami costitutivi e problema non lineare Cap. 3
3. Definizione dello stato di sforzo effettivo
Con riferimento ad un caso di sforzo uniassiale, sia F la forza applicata ad una sezione di un prisma
di base S. Lo sforzo risulta perciò:
σ = F per cui lo stato di sforzo reale è:
S
σ
F F
r = = =
σ
(3.4)
Sr
S⋅( 1−D)
(1−
D)
Dovendo essere 0 ≤D < 1 si deve necessariamente avere σr = σ per un materiale non danneggiato
(D = 0), e σr → ∞ per un materiale a rottura ( D →1). Si riporta come esempio i risultati in termini di
σ e di σ r di una prova di compressione:
Tensione (Mpa)
0 5 10 15
0 5 10 15 20 25 30 35 40
Spostamenti impressi (mm)
σ r
σ
Figura 3.2: Confronto tra sforzo effettivo e sforzo di Cauchy.
In caso di sforzo pluriassiale, dato che il rapporto S/S r non dipende dalla normale n l’operatore (1-D)
si applica a tutte le componenti del tensore degli sforzi, perciò :
σ
σ r =
(3.5)
( 1−
D)
44

Legami costitutivi e problema non lineare Cap. 3
4. Ipotesi d’equivalenza nelle deformazioni
Supponendo che il comportamento del materiale a deformazione non sia influenzato dal
danneggiamento si può affermare che :
il comportamento a deformazione monoassiale o pluriassiale di un materiale danneggiato, è ottenuto
dalla legge di comportamento del materiale vergine, in cui lo stato di sforzo sia quello reale [LeC].
σ
σ
σ r
1 2 3
⇒
D = 0 D D = 0
σ
σ
σ r
Figura 3.3: Equivalenza nelle deformazioni tra il materiale danneggiato sotto-posto a sforzo di Cauchy (2), e
lo stesso materiale sottoposto sforzo reale (3).
La legge d’elasticità lineare monodimensionale di un materiale danneggiato si scrive :
r
ε r = σ = σ
(3.6)
E (1 − D)
⋅ E
per cui si può definire un nuovo modulo E per il materiale danneggiato, pari a :
Er
= ( 1 − D)
⋅ E
(3.7)
Questa semplice scrittura mostra come il processo di danneggiamento riduce le caratteristiche
meccaniche del materiale. L’ipotesi introdotta non è rigorosa, in quanto suppone che i diversi
comportamenti del materiale (elasticità, viscosità ...) siano influenzati dalla variabile D tutti allo
stesso modo, ma la sua semplicità permette di formulare regole semplici ed efficaci.
45

Legami costitutivi e problema non lineare Cap. 3
5. La legge di evoluzione di Mazars
Il modello di Mazars [Maz],[MaC] è fondato sulle seguenti ipotesi :
1) Il materiale è elastico danneggiabile.
2) Il danneggiamento avviene a causa d’estensioni presenti lungo almeno una del-le direzioni
principali di deformazioni ε i.
3) Il danneggiamento è isotropo.
4) Il percorso di carico è monotono crescente.
5) Il danno evolve solo se si è superato un certo valore soglia.
Dato che il danno evolve a causa della presenza d’estensioni, e che il danneggiamento deve dipendere
da un’unica variabile scalare D, è necessario definire una deformazione equivalente (ε e ) che consenta
di caratterizzare lo stato d’estensione di un generico punto del materiale a partire dalle deformazioni
principali in esso presenti.
La definizione proposta da Mazars è :
2
∑ 〈 εi〉
i +
ε e =
(3.8)
Dove ε i rappresenta la deformazione principale nella direzione i
ε =
〈 i〉
+ εi se εi ≥ 0
ε i〉
= 0 se εi < 0
〈 +
La soglia di danneggiamento è quindi definita come:
f ( D)
= ε e − k(
D)
= 0
(3.9)
Dove k(D) =
ε d0 rappresenta la soglia d’inizio danneggiamento, pari alla deformazione di sforzo
massimo in una prova di trazione monoassiale. Sostituendo la definizione (3.8) nella (3.9) si trova,
nello spazio delle deformazioni principali, l’equazione di una sfera.
46

Legami costitutivi e problema non lineare Cap. 3
E’ così garantita la stessa importanza ad ognuna delle tre deformazioni principali. Nel rispetto della
diseguaglianza di Clausius-Duhem, l’equazione che regola l’evolversi del danneggiamento assume la
forma:
dD
dt
dD
dt
= 0
d〈
εe〉
= F(
ε e)
⋅
dt
+
se f = 0 e
se f = 0 e
df
dt
df
dt
< 0 o f < 0 (3.10)
= 0
Il danneggiamento può avvenire per sforzi di compressione o di trazione, nel primo caso le
estensioni si producono per effetto Poisson nella direzione perpendicolare allo sforzo, nel secondo si
verificano invece nella direzione parallela allo sforzo. Questi diversi comportamenti causano
dissimetria nella risposta di uno stesso materiale a sforzi di trazione e di compressione. Per cogliere
quest’aspetto è necessario introdurre nel modello due variabili scalari D t e D c , rappresentative del
danneggiamento in trazione ed in compressione, e governate da leggi d’evoluzione differenti. In caso
di sollecitazione uniassiale :
Dt = Ft( εe)
; Dc = Fc( εe)
(3.11)
In caso di sollecitazione pluriassiale entrambe le sollecitazioni contribuiscono all’evoluzione del
danneggiamento, per cui Mazars ha proposto di considerare la seguente combinazione:
D = α
α t ⋅ Dt
+ c ⋅ Dc
(3.12)
I parametri αt e αc sono definiti considerando la partizione del tensore degli sforzi nelle sue parti di
trazione e di compressione :
σ = 〈 σ 〉 σ
+ +〈 〉 −
47

Legami costitutivi e problema non lineare Cap. 3
Dove 〈 σ 〉 + indica la parte positiva del tensore degli sforzi mentre 〈 σ 〉 − la parte negativa. Attraverso
questa partizione si può giungere a definire le deformazioni legate agli sforzi positivi ed a quelli
negativi:
tr ( σ ) = tr(
〈 σ 〉 + ) + tr(
〈 σ 〉 −)
(3.13)
1+
ν ν
εt
= ⋅ 〈 σ 〉 − ⋅tr(
〈 σ
E E
+ 〉+
1+
ν ν
εc
= ⋅ 〈 σ 〉 − ⋅ tr(
〈 σ
E E
− 〉−
)
)
Infine i parametri αt e αc presenti nell’equazione (3.12) sono definiti come:
εti
⋅ ( εti
+ εci)
εti
⋅εi
α t = ∑ Hi
⋅
= ∑ Hi
⋅
(3.14)
i
2
i 2
εe
εe
α c =
∑
i
εci
⋅ ( εti
+ εci)
εci
⋅εi
Hi
⋅
= ∑ Hi
⋅
2
i 2
εe
εe
Con H i = 0 se εi ≥ 0 , ed H i = 0 se εi < 0 .
Per le variabili D t e D c sono state invece proposte, basandosi su risultati sperimentali, le seguenti
espressioni:
εd
0 ⋅ (1 − At)
At
Dt
= 1−
−
(3.15)
εe
exp( Bt
⋅ ( εe
− εd
0))
εd
0 ⋅ (1 − Ac)
Dc
= 1−
−
εe
exp( Bc
Ac
⋅ ( εe
− εd
0))
Dove ε do è la soglia d’inizio danneggiamento e A t , B t , A c , e B c sono dei parametri caratteristici del
materiale identificabili sperimentalmente con prove di compressione uniassiale (A c e B c ) e di
flessione (A t e B t ).
48

Legami costitutivi e problema non lineare Cap. 3
Assumendo A c = 1,1; B c = 1800; A t = 0,7; B t = 10000; ed0 = 0,0001; E = 1 KN/cm 2 ; ν = 0,2; le curve
D c e D t assumono il seguente aspetto :
1
Valore del danno
0.8
0.6
0.4
0.2
D t
D c
0
2.99
2.79
2.59
2.39
2.19
1.99
1.79
1.59
1.39
1.19
0.99
0.79
0.59
0.39
0.19
0
Deformazione equivalente (in millesimi)
Figura 3.4: Confronto tra l'evoluzione del danno a trazione con l'evoluzione a compressione.
In caso di sforzo uniassiale è possibile trovare analiticamente le curve (σ-ε). Infatti, le equazioni
(3.5.6-7-8) vengono riscritte come segue:
se lo sforzo è uniassiale di trazione secondo la direzione x :
αt = 1 ; αc = 0 ; D = D t (ε e ) = D t (ε x )
se lo sforzo è uniassiale di compressione secondo la direzione x :
αt = 0 ; αc = 1 ; D = D c (ε e ) = D c (ε y, ε z )
per cui utilizzando l’equazione (3.6) si ricava :
σ = ( 1− D)
⋅E⋅
εx (3.16)
49

Legami costitutivi e problema non lineare Cap. 3
con D = D t o D c , secondo i casi. Si hanno le due curve:
Tensione
0,0003
0,00025
0,0002
0,00015
0,0001
0,00005
0
σ c
σ t
Deformazione principale
Figura 3.5: Confronto tra curve di sforzo in materiale danneggiato a trazione o a compressione monoassiale (si
è usata una scala diversa per ogni curva).
Dai risultati numerici ottenuti (vedi par. 8.6) nel caso di compressione biassiale, si nota che il
modello sottostima di molto la resistenza ultima del materiale rispetto ai risultati sperimentali. Questa
è una conseguenza del fatto che il modello è stato formulato per campi di tensione uniassiale, e poi
esteso campi di tensioni pluriassiali. Si può ottenere un certo miglioramento dei risultati introducendo
un fattore correttivo γ( σi)
≤ 1 [Per] in modo che la nuova deformazione equivalente da usare nel solo
calcolo delle variabili D t e D c sia:
εe = γ( σi) ⋅ εe
con γ( σi)
=
∑
i
∑
i
(〈 σi〉
−)
(〈 σi〉
−)
2
(3.17)
50

Legami costitutivi e problema non lineare Cap. 3
6. La legge d’evoluzione di Cervera
Considerando una generica norma scalare τ t
del tensore delle deformazioni o del tensore delle
tensioni elastiche (non danneggiate) è possibile esprimere il criterio di danno [Cer] come :
t t t t
F( τ , r ) = τ − r ≤ 0 per ogni t ≥ 0 (3.18)
τ t viene chiamata deformazione equivalente, ed r t è il massimo valore raggiunto dalla norma τ t sino
all’istante considerato. Il valore iniziale r 0 è una proprietà del materiale, ed in ogni istante deve essere
r t
≥ r 0 . L’espressione (3.18) definisce una superficie limite nello spazio delle deformazioni o delle
tensioni elastiche. Il danno aumenta quando la norma τ t supera il massimo valore raggiunto da r, in
particolare il danno inizia quando la norma τ t supera il valore di soglia iniziale r 0 .
Ad ogni istante i valori del danno e di soglia verranno aggiornati secondo:
r t = max( r
0 , t
s ) con 0 ≤ s ≤ t
(3.19)
D
0
t
r ⎡ r ⎤
) = 1−
exp⎢A⋅
(1 − )
t
⎥
r ⎣ r ⎦
t
( r
0
con 0<
0 t
r ≤ r
(3.20)
La funzione (3.20) che definisce la variabile di danno risulta essere monotona crescente e di valori
compresi tra 0 ed 1.
La norma τ t definisce la forma della superficie limite di danno, per cui a seconda del modello di
danneggiamento considerato essa assumerà espressioni differenti.
• Modello di danno simmetrico a trazione e compressione.
Viene assunta la norma:
= 2 ⋅ Ψ
t
τ
e
ovvero
t t
τ = σ : C :
e
σ
t
e
(3.21)
51

Legami costitutivi e problema non lineare Cap. 3
Dove Υ e
è l’energia elastica corrispondente al materiale non danneggiato. Nello spazio delle tensioni
elastiche la superficie limite assume la forma di un ellissoide con centro nell’origine (una sfera se
ν =0). Il modello ha quindi la stessa resistenza a trazione che a compressione, perciò non è adeguato
allo studio di materiali come il calcestruzzo che possiede una resistenza a compressione circa 10 volte
superiore di quella a trazione.
• Modello con danno in sola trazione
La deformazione equivalente viene ridefinita come:
t t+ t+
τ = σ : C: σ
(3.22)
e
e
Dove σ t+ 1 2 3
e
= [ ] T
e
σ
e
σ
e
0 0 0
σ con σ e
i
pari alla tensione principale in direzione i se
questa è di trazione, 0 se è di compressione. Questa definizione coincide con quella precedente solo
nell’ottante delle tensioni triassiali di trazione, mentre nell’ottante di compressione triassiale
definisce un dominio non limitato.
• Modello con danneggiamento non simmetrico
E’ possibile definire un comportamento non simmetrico tra trazione e compres-sione eseguendo una
correzione di soglia nel modello simmetrico. L’espressione (3.21) viene sostituita da:
1 −θ
t
= σ
(3.23)
e
n
t
t
τ ( θ + ) ⋅ σ : C :
e
Dove n è il rapporto tra la massima resistenza a compressione (f c ) e la massima resistenza a trazione
(f t ), mentre θ dipende dallo stato tensionale:
3
∑i
∑
i
σ
= 1 e
θ = (3.24)
3
σ
i=
1
i
e
In particolare θ è 1 se le tensioni sono nel campo delle trazioni triassiali, 0 se sono nel campo delle
compressioni triassiale, un valore tra 0 e 1 negli altri casi.
52

Legami costitutivi e problema non lineare Cap. 3
f
σ
f
σ
f
f
f
σ
f
εu
f
σ
f
σ
f
σ
εu
f
σ
f
σ
f c
f
σ
εu
f c
f
Figura 3.6: Superfici limite per ν= 0 nei tre modelli: modello a danno simmetrico, modello con danno a sola trazione,
modello con danno a trazione e compressione.
Tutti i modelli dipendono da due parametri, r 0 ed A. r 0 governa l’inizio del danneggiamento, e viene
fissato (partendo da una prova di trazione monoassiale) pari a:
r
0
=
f
t
E
(3.25)
Per il parametro A si ricava l’espressione:
G
f
⋅ E 1 −1
A = ( − )
(3.26)
2
L ⋅ ( f ) 2
t
Dove E è il modulo di Young, G f è l’energia di frattura del materiale per unità di area, f t è la
resistenza massima a trazione, ed L è la lunghezza caratteristica dell’elemento finito (per elementi
triangolari CST si è usata
L = 2 ⋅ Area ).
53

Legami costitutivi e problema non lineare Cap. 3
Dovendo la funzione di danneggiamento essere monotona crescente, il parametro A non può essere
negativo. La condizione A ≥ 0 pone una limitazione sulle dimensioni degli elementi finiti:
G
f
⋅ E
L ≤ (3.27)
2
f )
( t
Valore danno
1
0,8
0,6
0,4
0,2
0
Aumento di A
0 1 2 3 4
Valore deformazione equivalente
Figura 3.7: Influenza del parametro A sull'evoluzione del danno.
1
Valore danno
0.8
0.6
0.4
0.2
0
Diminuzione di r 0
0 1 2 3 4
Valore deformazione equivalente
Figura 8: Influenza del valore di soglia sull’evoluzione del danno.
Esaminando la risposta uniassiale della legge σ – ε del modello di Cervera al variare dell’unico
parametro A, si nota che non viene rappresentata in maniera adeguata la risposta a compressione del
calcestruzzo (fig. 3.9) per cui vengono studiati altri legami.
54

Legami costitutivi e problema non lineare Cap. 3
-25
-25
-20
-20
Tensione (MPa)
-15
Tensione (MPa)
-15
-10
-10
-5
-5
0
0
-0.0005
-0.001
-0.0015
-0.002
0
0
-0.0005
-0.001
-0.0015
-0.002
Deformazione
Deformazione
Figura 3.9: Legame σ-ε uniassiale in compressione per A=0.8 e per A=0.4
7. La legge d’evoluzione di Rizzi
Mantenendo le leggi che descrivono la soglia di danneggiamento di Cervera, Rizzi propone la
seguente legge d’evoluzione del danno [Riz]:
D(
r
t
0 t
[ B ⋅ ( r − r )]
0
r
) = 1−
(1 − A)
⋅ − A⋅
exp
(3.28)
t
r
Anche questo legame (ideato per lo studio della meccanica delle rocce) non rappresenta bene il
comportamento del calcestruzzo.
55

Legami costitutivi e problema non lineare Cap. 3
8. La legge di evoluzione proposta per il modello isotropo
Volendo meglio rappresentare il tratto di softening del calcestruzzo, si ricerca una formula adatta per
la legge di evoluzione del danno. L’equazione analitica deve soddisfare le seguenti caratteristiche. Per
∂D
r = r 0 deve essere D = 0, per r = r 0 deve essere D = 0 e la derivata = 0
∂r
r=r0
L’equazione proposta è la seguente:
( t
) ⎡
= 1 − exp ⎢ ⋅ (1 r
D r
A −
⎣ r
t
) 2
0
⎤
⎥
⎦
(3.29)
con A un parametro dimensionale. Il legame uniassiale risulta ora:
5
0
-0.009 -0.008 -0.007 -0.006 -0.005 -0.004 -0.003 -0.002 -0.001 0 0.001 0.002
-5
-10
-15
-20
Tensione (MPa)
-25
-30
-35
Deformazione
-40
Figura 3.10: Relazione tensione - deformazione per la legge di danno proposta.
56

Legami costitutivi e problema non lineare Cap. 3
9. Un legame ortotropo
Oltre ai legami isotropi esposti nei precedenti paragrafi, si è implementato anche un legame
ortotropo, generalizzando in 3 dimensioni i legami uniassiali delle teorie costruite per analizzare stati
di sforzo in regime membranale (CFT, MCFT, RA-STM); ne risulta un legame a fessura rotante e
diffusa all’interno dell’elemento finito. Il procedimento seguito per il calcolo della matrice del
materiale nel sistema di riferimento globale è il seguente:
● Dalla soluzione elastica lineare ottenuta dall’analisi per elementi finiti, si ricavano le 3
deformazioni principali e le 3 direzioni principali utilizzando l’algoritmo di Jacobi sul tensore delle
deformazioni (si ricavano autovalori ed autovettori).
● Si forma la matrice di rigidezza del materiale nel sistema di riferimento principale, associando ad
ogni direzione principale una legge costitutiva uniassiale.Il modulo di Poisson viene assunto nullo,
per cui la matrice del materiale in questo sistema di riferimento risulta diagonale. Definendo il
parametro di softened ζ =
compressione sono:
1
1+
400⋅
ε eq
, i legami costitutivi considerati per il calcestruzzo in
Ramo ascendente: ( ε ≤ζ
⋅ )
(3.30)
d
ε 0
σ = ζ ⋅
d
f
'
c
⎡ ⎛ ε
d
⎞ ⎛ ε
d
⎞
⎢2
⎜
⎟ −
⎜
⎟
⎢⎣
⎝ζ
⋅ε
0 ⎠ ⎝ζ
⋅ε
0 ⎠
2
⎤
⎥
⎥⎦
Ramo discendente: ( ε > ζ ⋅ )
d
ε 0
2
⎡ ⎛ ε ⎤
d ⎞
⎢ ⎜ −1⎟
⎥
⎢ ⎜ ζε
0
σ
⎟ ⎥
d
= ζ ⋅ f '
c
1 −
⎢ ⎜ ⎟
(3.31)
2 ⎥
⎢ ⎜ −1
⎟ ⎥
⎢⎣
⎝ ζ ⎠ ⎥⎦
57

Legami costitutivi e problema non lineare Cap. 3
Il parametro di softened ha lo scopo di ridurre la legge costitutiva a compressione del calcestruzzo,
per tener conto della differenza di comportamento tra un calcestruzzo appartenente ad una struttura
reale ed un calcestruzzo appartenente ad un provino sottoposto a compressione.
Figura 3.11: Legame uniassiale del calcestruzzo compresso.
L’effetto di una tensione trasversale di trazione modifica la legge a compressione riducendone sia il
valore di sforzo massimo sia la relativa deformazione. Per definire il parametro di softened
ζ =
1
1+
400
⋅ε eq
si definisce una deformazione di trazione trasversale equivalente, se la direzione
delle compressioni è la 1, si assume
2
3
2
ε
eq
= ε 2
+ ε dove ε
2
vale 0 se la deformazione è di
compressione, ε
2
se è di trazione.
Per il calcestruzzo in trazione si utilizza il seguente legame:
Ramo ascendente: ( ε ≤ ε ) σ
r
= Ec
⋅ε
r
= 3 .875 f '
c
⋅ε
r
(3.32)
r
cr
Ramo discendente: ε > ε
r
cr
0.4
⎛ ε
cr
⎞
0 ⎛ 0.00008
.31 '
⎟ ⎞
σ ⎜
⎟ = ⋅
⎜
r
= f
cr
f
c
(3.33)
⎝ ε
r ⎠
⎝ ε
r ⎠
0.4
58

Legami costitutivi e problema non lineare Cap. 3
Figura 3.12: Legame uniassiale del calcestruzzo in trazione.
In tutte le formule precedenti si è assunto
E
c
= 3875 f ' [MPa] (Modulo elastico del calcestruzzo),
ε = 0.00008 (Deformazione di fessurazione), = 0.31 f ' c [MPa] (Tensione di fessurazione).
cr
Il generico modulo G, viene formato come:
f cr
c
G
ij
Ei
⋅E
j
= (3.34)
E + E
i
j
● Formata la matrice D nel sistema di riferimento principale, si ricavano le proprietà del materiale
nel sistema globale tramite la relazione
D
XYZ
= T
T
⋅D
123
⋅T
dove [L3], [VMW]:
2
2
2
⎡ l
⎤
1
m1
n1
l1
⋅m1
m1
⋅n1
l1⋅n1
⎢ 2
2
2
⎥
⎢ l2
m2
n2
l2
⋅m2
m2
⋅n2
l2
⋅n2
⎥
⎢
2
2
2
l
⎥
3
m3
n3
l3
⋅m3
m3
⋅n3
l3
⋅n3
T = ⎢
⎥
(3.35)
⎢2⋅l1
⋅l2
2⋅m1
⋅m2
2⋅n1
⋅n2
l1
⋅m2
+ l2
⋅m1
m1
⋅n2
+ m2
⋅n1
n1
⋅l2
+ n2
⋅l1
⎥
⎢2⋅l
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⎥
2
l3
2 m2
m3
2 n2
n3
l2
m3
l3
m2
m2
n3
m3
n2
n2
l3
n3
l2
⎢
⎥
⎢⎣
2⋅l3
⋅l1
2⋅m3
⋅m1
2⋅n3
⋅n1
l3
⋅m1
+ l1⋅m3
m3
⋅n1
+ m1
⋅n3
n3
⋅l1
+ n1
⋅l3
⎥⎦
avendo indicato con l m n i coseni direttori della terna principale rispetto al sistema X Y Z.
i
i
i
59

Legami costitutivi e problema non lineare Cap. 3
● Calcolate le proprietà del materiale nel sistema di riferimento principale, la matrice di rigidezza
dell’elemento finito viene calcolata in modo analogo al caso isotropo.
10. Legami costitutivi dell’acciaio
Per l’acciaio normale il legame più semplice è quello bilatero simmetrico, di tipo elastico
perfettamente plastico. Si assume quindi:
σ
E ε
s
=
s
⋅
s
per
s y
ε < ε ramo elastico lineare (3.36)
σ
s
= f y
per ε
s
≥ ε
y
ramo plastico (3.37)
dove
E
s
: Modulo elastico delle armature, f
y
: Valore dello sforzo di snervamento dell’ armatura.
Questo modello rappresenta bene la risposta di un provino di acciaio in una prova di trazione, il
comportamento delle barre d’armatura immerse (embedded) nel calcestruzzo è però diverso. La
differenza più importante è l’abbassamento della tensione
f
y
; inoltre, dopo lo snervamento, il
comportamento della barra immersa nel calcestruzzo è di difficile determinazione in quanto la
deformazione dell’acciaio nella zona di fessura cresce rapidamente. Un legame costitutivo più vicino
al reale comportamento dell’acciaio immerso nel calcestruzzo prevede le seguenti equazioni
costitutive [L22], [Vec]:
f
= ⋅ε
Ramo elastico, fig. 3.13 ( ε
s
≤ ε
n
) (3.33)
s
E s
f = f
s
y
s
⎡
ε ⎤
s
⎢( 0 .91−2B) + ( 0.02+
0.25B)
. ⎥ Ramo di incrudimento, fig. 3.13 ( ε
s
> ε
n
) (3.34)
⎢⎣
ε
y ⎥⎦
Essendo ε
n
la deformazione media di snervamento delle barre d’acciaio avvolte dal calcestruzzo
misurata all’inizio dello snervamento effettivo e pari a =ε ( 0.93−
B)
ε .
n y
2
60

Legami costitutivi e problema non lineare Cap. 3
Il parametro
⎛ 1 ⎞⎛
B=
⎜ ⎟⎜
⎝ ρ ⎠
⎝
f
f
cr
y
⎞
⎟
⎠
1.5
è il termine associato allo snervamento apparente delle barre.
Figura 3.13: Legame uniassiale per l'acciaio immerso nel calcestruzzo.
Per l’acciaio di precompressione il modello assunto è quello di Ramberg-Osgood [MC90]:
f
p
= E ( E + ε ) Ramo elastico, fig. 3.14 ( f 0. 7 f )
ps
dec
s
p
≤ (3.35)
pu
'
E
ps
( ε
dec
+ ε
s
)
'
( E ( ε + ))/
f
= Ramo di incrudimento, fig. 3.14 ( f
[ { } ] m 1
1 +
m
p
0. 7 f
pu
)
ps dec
ε
s pu
f
p
/
> (3.36)
Figura 3.14: Legame uniassiale per l'acciaio da precompressione.
61

Legami costitutivi e problema non lineare Cap. 3
10. Cenni sulla regolarizzazione della risposta non lineare
L’implementazione di un codice di calcolo che studi il ramo di “softening” di un materiale presenta
numerose difficoltà. Una di queste è la localizzazione del danneggiamento in zone di volume tendenti
a zero, quando il diagramma sforzi deformazioni manifesta pendenza negativa. Questo
comporterebbe l’annullarsi dell’energia dissipata dalla struttura, fenomeno fisicamente non realistico.
Per ovviare questo inconveniente si sono studiati dei metodi di regolarizzazione, che tramite
l’introduzione di una lunghezza caratteristica dipendente dal materiale, governano l’ampiezza della
zona nella quale si concentrano i fenomeni anelastici [Per],[BoM2]. La regolarizzazione del modello
a danno può avvenire con uno dei seguenti metodi [Mai]:
● Regolarizzazione basata sull’energia di frattura.
I parametri che governano il softening del materiale vengono modificati al variare della mesh, in
modo che l’energia di frattura associata all’elemento finito rimanga costante.
● Modello di danno non locale.
Si considera che l’evoluzione del danno in un punto sia governato dalla media pesata su di un volume
rappresentativo di materiale, anziché solo dal suo valore puntuale.
● Modello di danno con gradiente di ordine superiore.
Si assume che il comportamento del materiale in un punto dipenda non solo dal valore del danno in
quel punto, ma anche dal suo gradiente.
● Regolarizzazione viscosa.
Si introduce nel modello una dipendenza dal tempo mediante un parametro di viscosità fittizia.
Il modello a danno isotropo di Cervera, utilizza una regolarizzazione basata sull’energia di frattura,
difatti il parametro
G
f
⋅ E 1 −1
A = ( − ) viene ricavato in modo che i vari elementi della mesh
2
L ⋅ ( f ) 2
t
abbiano la stessa energia di frattura. Nella formula per ricavare A, il parametro L (lunghezza
caratteristica dell’elemento finito) caratterizza la dimensione dei singoli elementi.
62

Legami costitutivi e problema non lineare Cap. 3
Il modello ortotropo viene invece regolarizzato utilizzando un danno non locale [BoM2]. Definita
una grandezza caratteristica per la struttura λ (che può essere l’altezza della trave in caso di travi
inflesse) in ogni punto di Gauss viene calcolata una deformazione non locale pari a:
~ ε = c⋅ε
+ (1−
c)
⋅
∑
i
ε(
ξ ) ⋅w(
ξ )
∑
i
w(
ξ )
dove la sommatoria sull’indice i è riferita a tutti i valori di deformazione appartenenti ad una sfera
centrata nel punto corrente di raggio pari a
2 ⋅λ
, ξ è la distanza dal punto corrente al generico punto
interno alla sfera e w è il peso da assegnare alle varie deformazioni. La funzione peso w è stata
assunta pari a
2
−(
ξ / λ )
w(
ξ ) =e mentre alla costante c è stato assegnato un valore di 0.9.
11. Metodo della secante per la soluzione di problemi non lineari
Se il materiale è non lineare elastico, l’equazione costitutiva non dipende dalla storia di carico.
L’equazione di equilibrio per il singolo elemento è:
K ⋅ S = R
(3.37)
e
e
dove
K è la matrice di rigidezza secante:
e
K
e
= ∫ B ⋅ D ⋅ B ⋅ dV
(3.38)
V
T
la matrice costitutiva D conterrà i moduli secanti del materiale. Assemblando le (3.38) si trova un
sistema di equazioni algebriche non lineari, la cui soluzione si ottiene col metodo iterativo della
secante.
63

Legami costitutivi e problema non lineare Cap. 3
Alla i-esima iterazione si ha:
( i− 1) ( i)
K ⋅ S = R
t
t
(3.39)
dove la matrice di rigidezza secante è calcolata alla iterazione precedente come:
K
( i− 1) T ( i−1)
e
= ∫ B
V
⋅ D
⋅ B ⋅ dV
(3.40)
La soluzione viene eseguita in modo automatico con le seguenti operazioni. Supponiamo di applicare
il carico R totale (lo schema seguente è valido nel caso di un modello a danno isotropo, la
generalizzazione ad legame anisotropo è immediata).
Iterazione i = 1
Calcolo della matrice di rigidezza col modulo iniziale, per tutti gli elementi.
K
(0)
e
= ∫ B
V
T
⋅ D
(0)
⋅ B ⋅ dV
Assemblaggio e risoluzione del sistema lineare.
(0)
K ⋅ S = R
t
(1)
t
Calcolo della deformazione degli elementi.
ε
(1)
= B ⋅ S
(1)
Valutazione del danneggiamento per ogni elemento, calcolo della tensione di Cauchy e della nuova
matrice costitutiva.
64

Legami costitutivi e problema non lineare Cap. 3
σ
(1)
(0)
= D ⋅ d
(1) (1)
( 1−
) ⋅ε
D
(1)
= D
(0)
⋅ (1 − d
(1)
)
Calcolo delle forze interne equivalenti alle tensioni di Cauchy per ogni elemento.
F
(1)
e
= ∫ B
V
T
⋅σ
(1)
⋅ dV
Assemblaggio delle forze interne e calcolo dello squilibrio.
P
(1)
(1)
t
= R − F t
F
Squilibrio alla seconda iterazione
R
1 2 i
Punto di equilibrio teorico
Punto di equilibrio numerico
S(1) S(2) S(i)
S
Figura 3.15: Metodo della matrice secante.
Iterazione i = 2
Calcolo della matrice di rigidezza col modulo iniziale, per tutti gli elementi.
K
(1)
e
= ∫ B
V
T
⋅ D
(1)
⋅ B ⋅ dV
Assemblaggio e risoluzione del sistema lineare.
65

Legami costitutivi e problema non lineare Cap. 3
(1)
K ⋅ S = R
t
(2)
t
Calcolo della deformazione degli elementi.
ε
(2)
= B ⋅ S
(2)
Valutazione del danneggiamento per ogni elemento, calcolo della tensione di Cauchy e della nuova
matrice costitutiva.
σ
(2)
(0)
= D ⋅ d
(2) (2)
( 1−
) ⋅ε
D
(2)
= D
(0)
⋅ (1 − d
(2)
)
Calcolo delle forze interne equivalenti alle tensioni di Cauchy per ogni elemento.
F
(2)
e
= ∫ B
V
T
⋅σ
(2)
⋅ dV
Assemblaggio delle forze interne e calcolo dello squilibrio.
P
(2)
(2)
t
= R − F t
Il procedimento iterativo prosegue finché non viene soddisfatto un opportuno criterio di convergenza
[L2, L6, L18, L19]. Un primo criterio è quello di determinare la norma dell’incremento di
spostamento e rapportarla alla norma dello spostamento corrente; si raggiunge convergenza quando
tale rapporto è minore di una quantità prefissata:
S
( i)
− S
S
( i)
( i−1)
≤ δ
1
(3.41)
66

Legami costitutivi e problema non lineare Cap. 3
Un altro criterio si basa sulla norma delle forze residue rapportata alla norma dei carichi esterni:
R − F
R
( i)
≤ δ
2
(3.42)
Un terzo criterio può essere quello di rapportare la norma sul lavoro fatto rispetto al lavoro iniziale:
( R − F
( i)
T
)
( R − F
⋅ ( S
(1)
)
( i)
T
− S
⋅ S
(1)
( i−1)
)
≤ δ
3
(3.43)
Come norma viene generalmente usata la norma euclidea.
Il procedimento viene invece arrestato nel caso di mancata convergenza della soluzione nel numero
massimo di iterazioni previste. Questa situazione è in genere associata ad una condizione di carico
che supera la capacita portante della struttura. La tecnica risolutiva secante presenta dei vantaggi e
degli svantaggi. La matrice di rigidezza secante è definita positiva per cui il procedimento iterativo
risulta molto più affidabile rispetto ad altri algoritmi. La velocità di convergenza del metodo secante è
però più bassa essendo un metodo del primo ordine. La limitazione fondamentale dell’impostazione
secante risiede però nell’ipotizzare un legame costitutivo dei materiali elastico non lineare per cui
non è possibile cogliere i fenomeni isteretici.
Altri algoritmi numerici utilizzati nella risoluzione di problemi non lineari sono il metodo di Newton
ed i metodi di Newton modificati. Questi metodi sono di tipo incrementale, e sono più adatti, rispetto
al metodo secante, a seguire una storia di carico complicata.
Il metodo di Newton, o metodo della matrice tangente, in particolare converge con velocità di
convergenza 2 se la soluzione di partenza nella generica iterazione, è sufficientemente vicina alla
soluzione esatta.
67

Applicazioni in campo elastico lineare Cap. 4
CAP. 4
Applicazioni in campo elastico lineare
Indice riassuntivo delle applicazioni riportate
Esempi eseguiti con tutti i 3 codici di calcolo implementati (integrazione completa, integrazione
selettiva, funzioni di forma non compatibili) :
- Patch Test per l’elemento solido integrato in modo selettivo.
- Patch Test per l’elemento solido aventi funzioni di forma non compatibili.
- Analisi una mensola snella e soggetta ad un carico concentrato.
- Analisi di una trave doppiamente incastrata e soggetta ad un carico uniforme.
Esempi eseguiti col solo codice di calcolo operante con funzioni non compatibili:
- Studio della deformabilità trasversale e dell’ingobbimento sezionale di un elemento in
parete sottile a profilo rettangolare chiuso.
Esempi eseguiti col solo codice di calcolo operante ad integrazione selettiva:
- Patch Test per l’elemento solido con acciaio diffuso.
- Patch Test per l’elemento solido con acciaio embedded.
- Patch Test per l’elemento solido presollecitato.
- Pilastro soggetto a peso proprio.
- Studio di una pila da ponte a profilo misto in campo elastico lineare.
68

Applicazioni in campo elastico lineare Cap. 4
1. Patch Test per l’elemento solido integrato in modo selettivo
Il Patch Test è stato introdotto dal Prof. Irons come mezzo per verificare la convergenza di un
elemento finito non compatibile. In questo lavoro viene eseguito sia per testare il codice di calcolo
implementato, sia per verificare la correttezza della soluzione ottenuta tramite l’integrazione selettiva
(e quindi con presenza di modi deformativi ad energia nulla). Tutte le prove numeriche sono state
eseguite sia con un modulo di Poisson nullo, sia pari a 0.2.
Il Patch Test di esegue nel seguente modo.
1) Si forma una maglia di elementi contenenti almeno un nodo interno. Le maglie devono
essere non regolari in modo da prevenire eventuali compensazioni di errore per simmetria. La maglia
scelta in questo lavoro, riproduce un cubo di lato 2 suddiviso in 8 cubi di lato 1. Se la maglia non
fosse distorta il nodo centrale avrebbe avuto coordinate pari a 0,0,0; è stato invece imposto che il
punto centrale avesse coordinate 0.2,0.1,0.3 in modo da ottenere un cubo regolare dall’assemblaggio
di 8 elementi distorti.
z
y
x
Figura 5.1: Rappresentazione della struttura utilizzata nel Patch Test.
2) Si assumono arbitrariamente che dei polinomi P i (x,y,z) siano la soluzione del problema
negli spostamenti u (in X), v (in Y) e w (in Z).
69

Applicazioni in campo elastico lineare Cap. 4
3) Si calcolano i valori di P i , k nei nodi esterni della mesh, e si effettua una prova numerica
imponendo i valori P i,k e controllando che gli spostamenti calcolati nel nodo centrale coincidano coi
valori ottenibili dai polinomi imposti.
a) Prova di trazione uniassiale
Si impone uno spostamento in direzione X pari a 1.0 per i nodi con coordinata x = 1.0, 0.5 per i nodi
con coordinata x = 0.0 e 0.0 per i nodi di coordinata –1.0. Tutti gli altri spostamenti dei nodi esterni
vengono imposti nulli. Alla struttura rimangono così solamente i 3 gradi di libertà relativi al nodo
interno.
La soluzione imposta prevede i seguenti spostamenti:
u ( x , y,
z)
= 0.5 ⋅(1.0
+ x)
In direzione X
v ( x,
y,
z)
= 0.0
In direzione Y
w ( x,
y,
z)
= 0.0
In direzione Z
Per il nodo centrale si deve ottenere uno spostamento pari a u = 0 .5 ⋅(0.2+
1) = 0. 6
Il risultato numerico ottenuto è
u = 6.000000000000002E-001
v = 1.242266312400961E-017
z = -8.848897666825595E-018
Mentre in termini di tensioni in tutti gli elementi risulta:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
2 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
3 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
4 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
5 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
6 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
7 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
8 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
9 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
70

Applicazioni in campo elastico lineare Cap. 4
Stesse tensioni negli altri elementi. Dato che si è assunto un modulo di elasticità pari a 40.0 ed un
∆ 1.0
modulo di Poisson pari a 0.0, σ = E ⋅ ε = E ⋅ = 40 .0 ⋅ = 20. 0 il risultato appare corretto.
Lato 2.0
Questa stessa prova numerica è stata eseguita anche per un nodo interno di coordinate x = 0.1, y =
0.2, z = 0.3 e per x = 0.0, y = 0.0, z =0.0, poiché non è detto che se la soluzione calcolata è corretta
per una posizione del nodo centrale, lo sia anche per altre posizioni. In tutte le prove eseguite i
risultati sono stati comunque corretti.
La prova è stata quindi ripetuta utilizzando un modulo di Poisson pari a 0.2. La soluzioni in termini di
spostamento non deve essere influenzata dal valore del modulo di Poisson, per cui ci si attende uno
spostamento del nodo centrale pari a 0.6 in direzione X.
Essendo impedita la contrazione laterale, nasceranno però delle tensioni anche in direzione Y e Z, e la
tensione in X risulterà maggiore rispetto al caso studiato in precedenza. Chiamando ∆ il generico
cedimento imposto sulla faccia del cubo e b il lato del cubo, è possibile, utilizzando il metodo delle
forze, scrivere il seguente sistema:
⎡ b
⎢ E
⎢
⎢ ν ⋅ b
⎢−
⎢
E
⎢ ν ⋅ b
⎢−
⎣ E
ν ⋅ b
−
E
b
E
ν ⋅ b
−
E
ν ⋅ b⎤
− ⎥ ⎡σ
x ⎤ ⎡∆
E
⎥ ⎢ ⎥ ⎢
ν ⋅ b⎥
⎢ ⎥ ⎢
− ⎥ ⋅ ⎢σ
⎥ = ⎢
y
∆
E
⎥ ⎢ ⎥ ⎢
⎥ ⎢ ⎥ ⎢
b
⎥ ⎢
⎣σ
⎥
⎦
⎢
z ⎣∆
E ⎦
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
x
y
z
(5.1)
risolvendo il (5.1) è possibile ricavare la soluzione corretta in termini di tensioni, dati i cedimenti
imposti sulle facce. Nel caso in esame si ottieneσ
22 .2 σ = 5.5 σ = 5. 5
L’elaborazione numerica fornisce in termini di spostamento:
x
=
y
z
u = 6.000000000000000E-001
v = 3.337805100953997E-017
w = -3.929851842769097E-017
71

Applicazioni in campo elastico lineare Cap. 4
Mentre in termini di tensioni in tutti gli elementi risulta:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .2222E+02 .5556E+01 .5556E+01 .0000E+00 .0000E+00 .0000E+00
2 .2222E+02 .5556E+01 .5556E+01 .0000E+00 .0000E+00 .0000E+00
3 .2222E+02 .5556E+01 .5556E+01 .0000E+00 .0000E+00 .0000E+00
***
7 .2222E+02 .5556E+01 .5556E+01 .0000E+00 .0000E+00 .0000E+00
8 .2222E+02 .5556E+01 .5556E+01 .0000E+00 .0000E+00 .0000E+00
9 .2222E+02 .5556E+01 .5556E+01 .0000E+00 .0000E+00 .0000E+00
Questa setessa prova numerica è stata eseguita anche per un nodo interno di coordinate x = 0.1, y =
0.2, z = 0.0 e per x = 0.0, y = 0.0, z =0.0, in tutte le prove eseguite i risultati sono corretti.
b) Prova di taglio puro
Si impone uno spostamento in direzione Y pari ad 1.0 a tutti i nodi con Z = 1.0 e uno spostamento
pari a 0.5 nei nodi con Z = 0.5. Ovvero si impone uno spostamento che soddisfi i polinomi:
u ( x,
y,
z)
= 0.0
In direzione X
v ( x , y,
z)
= 0.5 ⋅(1.0
+ z)
In direzione Y
w ( x,
y,
z)
= 0.0
In direzione Z
Lo spostamento del nodo centrale deve perciò risultare v = 0 .5 ⋅(1.0
+ 0.2) = 0. 6 sia con modulo di
Poisson nullo che con modulo di Poisson pari a 0.2.
Le uniche tensioni non nulle saranno le τ yz che dovranno valere:
per ν = 0.0 γ = 0.5 τ = 10.0
per ν = 0.2 γ = 0.5 τ = 8 . 3
72

Applicazioni in campo elastico lineare Cap. 4
Per ν = 0.0 l’elaborazione numerica fornisce in termini di spostamento:
u = 6.987782965174495E-018
v = 6.000000000000001E-001
w = 4.119739619340261E-017
Mentre in termini di tensioni, in tutti gli elementi risulta:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .1000E+02 .0000E+00
2 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .1000E+02 .0000E+00
3 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .1000E+02 .0000E+00
* * *
8 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .1000E+02 .0000E+00
9 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .1000E+02 .0000E+00
Per ν = 0.2 l’elaborazione numerica fornisce in termini di spostamento:
u = -1.609447109364453E-017
v = 6.000000000000002E-001
w = 2.593942896853087E-017
Mentre in termini di tensioni, in tutti gli elementi risulta:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .8333E+01 .0000E+00
2 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .8333E+01 .0000E+00
* * *
7 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .8333E+01 .0000E+00
8 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .8333E+01 .0000E+00
9 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .8333E+01 .0000E+00
Questa stessa prova numerica è stata eseguita anche per un nodo interno di coordinate x = 0.1, y =
0.2, z = 0.0 e per x = 0.0, y = 0.0, z =0.0, in tutte le prove eseguite i risultati sono corretti.
73

Applicazioni in campo elastico lineare Cap. 4
c) Prova di taglio – trazione
Viene eseguita una prova di taglio più trazione nel solo caso con modulo di Poisson pari a 0.2. Il
taglio viene imposto come nel caso b) mentre la trazione come nel caso a) con un valore pari a 0.6
nella faccia esterna del cubo. I risultati esatti si deducono sovrapponendo gli effetti del caso b) con
0.6 volte gli effetti del caso a). Gli spostamenti imposti soddisfano i polinomi:
u ( x,
y,
z)
= 0.3⋅
(1.0 + x)
In direzione X
v ( x,
y,
z)
= 0.5⋅
(1.0 + z)
In direzione Y
w ( x,
y,
z)
= 0.0
In direzione Z
Nel nodo centrale dovrà risultare u = 0 .3 ⋅(0.2+
1) = 0. 36 e v = 0 .5 ⋅(1.0
+ 0.2) = 0. 6 mentre le tensioni
dovranno essere costanti e pari a :
σ
x
=
y
z
yz
22 .2 ⋅ 0.6 = 13.3 σ = 5.5 ⋅ 0.6 = 3.3 σ = 5.5 ⋅ 0.6 = 3.3 τ = 8.3
L’elaborazione numerica fornisce in termini di spostamento:
u = 3.600000000000000E-001
v = 6.000000000000000E-001
w = 4.290914885448565E-017
Mentre in termini di tensioni, in tutti gli elementi risulta:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
2 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
3 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
4 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
5 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
6 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
7 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
8 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
9 .1333E+02 .3333E+01 .3333E+01 .0000E+00 .8333E+01 .0000E+00
74

Applicazioni in campo elastico lineare Cap. 4
2. Patch test per l’elemento solido aventi funzioni di forma non compatibili
Il test sull’elemento non compatibile viene inizialmente eseguito su di una mesh non distorta (senza
però piani di simmetria, punto centrale x = 0.2, y = 0.1, z = 0.3).
z
y
x
Figura 5.2: Mesh per il Patch Test dell'elemento incompatibile.
Viene eseguita la prova di trazione vista nel punto a), si riportano i risultati in termini di spostamento:
u = 5.000000000000000E-001
v = 9.535333435268551E-034
w = 4.633301234482236E-017
Il test da risultati corretti. Il punto centrale viene ora portato a x = 0.35, y = 0.10, z = 0.30 di
conseguenza il cubo sarà formato da 8 esaedri irregolari. Essendo la trazione in direzione X, lo
1
spostamento del punto centrale sarà 1 .35 ⋅ = 0. 675 .
2
75

Applicazioni in campo elastico lineare Cap. 4
I risultati in termini di spostamento:
u =6.760914893916842E-001
v = 3.044309783847875E-017
w = 2.938330877047082E-017
Il test da risultati non corretti per lo spostamento in direzione X. Il punto centrale viene ora portato a
x = 0.35, y = 0.20, z = 0.30. Non avendo modificato la coordinata in direzione X, ci si aspetta di
ritrovare gli stessi risultati, invece in termini di spostamento si trova:
u = 6.760995594447284E-001
v = 1.781093657018022E-003
w = 2.598975706585580E-017
Si noti che non solo compare uno spostamento in direzione Y che non ha ragione di esistere, ma
cambia anche lo spostamento in direzione X senza che sia stata modificata la coordinata del punto
centrale in quella direzione. Il Patch Test da quindi dei risultati non corretti. Lo stesso problema
risolto con l’esaedro a integrazione completa e con l’esaedro a integrazione selettiva fornisce:
Integrazione completa:
u = 6.750000000000002E-001
v = 1.099285665512805E-018
w = -8.917688029245993E-018
Integrazione selettiva:
u = 6.750000000000002E-001
v = 1.176290574752829E-018
w = 1.162143382850229E-017
Come specificato in [Hughes] la formulazione dell’elemento incompatibile alla Wilson può dar luogo
a dei risultati sbagliati in un Pacht Test con elementi distorti, come anche comprovato da numerosi
studi numerici e teorici [Lesaint]. Il problema è stato risolto da Taylor, grazie alla formulazione di un
elemento incompatibile modificato [Taylor]. In questo lavoro il codice di calcolo ad Elementi Finiti
Incompatibili verrà utilizzato solo con mesh non distorte, per cui non viene introdotta la modifica
apportata da Taylor.
76

Applicazioni in campo elastico lineare Cap. 4
3. Analisi di una mensola snella
Per testare la qualità dei 3 metodi di soluzioni studiati (integrazione completa, integrazione selettiva e
funzioni di forma non compatibili) si esegue l’analisi di una mensola snella. La sezione della mensola
viene discretizzata tramite 2 elementi finiti accoppiati nel senso della larghezza, in modo da avere 1
solo elemento finito lungo l’altezza della mensola. L’uso di 2 elementi accoppiati è necessario per
impedire il propagarsi dei modi spuri torsionali durante l’analisi con l’integrazione selettiva. La
sezione della mensola ha lato 20 x 20 cm, mentre la sua lunghezza è pari a 4 m (rapporto L/h = 20). Il
materiale ipotizzato possiede un modulo di Young E = 30000 MPa ed un modulo di Poisson pari a
0.0 o 0.2 a seconda dei casi. La mensola è considerata incastrata ad un estremo e caricata nell’altro
con una forza pari a 800 N. La soluzione di De Saint Venant in termini di freccia e rotazione
dell’estremo caricato, fornisce:
3
3
P ⋅ L 800 ⋅ 4000
f = =
= 4.26
8
3 ⋅ E ⋅ I 3 ⋅ 30000 ⋅1.3
⋅10
mm
ϕ =
P ⋅ L
2
2
800 ⋅ 4000
=
2 ⋅ 30000 ⋅1.3
⋅10
8
2 ⋅ E ⋅ I
= 0.16
L’analisi numerica è stata eseguita infittendo la discretizzazione lungo l’asse della mensola da 1 a 64
suddivisioni, ottenendo così le curve di convergenza per ognuno dei tre metodi di soluzione.
77

Applicazioni in campo elastico lineare Cap. 4
Spostamenti impediti
Forze nodali applicate
200
100
Figura 5.3: Modello utilizzato con 4 suddivisioni lungo l'asse.
Dalle elaborazioni eseguite si nota che se il modulo di Poisson è nullo la soluzione calcolata con
l’integrazione selettiva coincide (per il caso studiato) con la soluzione trovata impiegando le funzioni
di forma incompatibili. La soluzione in termini di freccia è già ottimamente approssimata impiegando
solamente 4 elementi lungo l’asse, mentre in termini di rotazione della sezione caricata la soluzione
coincide con quella di DSV anche con una sola suddivisione. La soluzione calcolata tramite
l’integrazione completa non è paragonabile, in termini di accuratezza, con quelle derivanti dagli altri
metodi. Per ottenere la stessa precisione di 4 suddivisioni con elementi incompatibili o integrati in
modo selettivo, occorrono 64 suddivisioni con elementi operanti con integrazione completa.
Se il modulo di Poisson non è nullo, la soluzione derivante dagli elementi solidi con integrazione
selettiva, converge ad un valore minore rispetto a quella calcolata con le funzioni di forma non
compatibili.
78

Applicazioni in campo elastico lineare Cap. 4
4.5
4
3.5
3
freccia (mm)
2.5
2
1.5
1
Freccia Selettiva / Incompatibili
Freccia Completa
Freccia De Saint Venant
0.5
0
0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64
Divisioni in asse
Figura 5.4: Curve di convergenza dei 3 metodi studiati, per l'abbassamento della sezione caricata (ν = 0).
0.18
0.16
0.14
0.12
Rotazione
0.1
0.08
0.06
0.04
Selettiva / Incompatibili /
De Saint Venant
Completa
0.02
0
0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64
Divisioni in asse
Figura 5.5: Curve di convergenza dei 3 metodi studiati, per la rotazione della sezione caricata (ν = 0).
79

Applicazioni in campo elastico lineare Cap. 4
4.5
4
3.5
3
Freccia (mm)
2.5
2
1.5
1
Selettiva
Completa
De Saint Venant
Incompatibile
0.5
0
0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64
Divisioni in asse
Figura 5.6: Curve di convergenza dei 3 metodi studiati, per l'abbassamento della sezione caricata (ν = 0.2).
0.18
0.16
0.14
0.12
Rotazione
0.1
0.08
0.06
0.04
Selettiva
Completa
Incompatibili
De Saint Venant
0.02
0
0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64
Divisioni in asse
Figura 5.7: Curve di convergenza dei 3 metodi studiati, per la rotazione della sezione caricata (ν = 0.2).
80

Applicazioni in campo elastico lineare Cap. 4
4. Analisi di una trave doppiamente incastrata
Come secondo esempio per testare la qualità dei 3 metodi di soluzioni studiati (integrazione
completa, integrazione selettiva e funzioni di forma non compatibili) si esegue l’analisi di una trave
incastrata alle due estremità e soggetta ad un carico distribuito. I modelli su cui sono state eseguite le
elaborazioni numeriche sono gli stessi dell’esempio precedente (con un cambio di vincolo e di
carico). Il materiale ipotizzato possiede sempre un modulo di Young E = 30000 MPa ed un modulo di
Poisson pari a 0.0 o 0.2 a seconda dei casi. Il carico distribuito su tutta la campata è fissato a 1000
N/m. La soluzione di De Saint Venant in termini di freccia massima (in mezzeria) fornisce:
4
4
P ⋅ L 1⋅
4000
f = =
= 0.16
8
384 ⋅ E ⋅ I 384 ⋅ 30000 ⋅1.3
⋅10
mm
Spostamenti impediti
Forze nodali applicate
100
200
Spostamenti impediti
Figura 5.8: Modello utilizzato con 4 suddivisioni lungo l'asse.
Si espongono ora i risultati delle elaborazioni eseguite con modulo di Poisson nullo.
81

Applicazioni in campo elastico lineare Cap. 4
1.80E-01
1.60E-01
1.40E-01
1.20E-01
Freccia (mm)
1.00E-01
8.00E-02
6.00E-02
4.00E-02
Selettiva / Incompatibile
Completa
De Saint Venant
2.00E-02
0.00E+00
0 10 20 30 40 50 60
Divisioni in asse
Figura 5.9: Convergenza sulla freccia in mezzeria dei 3 metodi analizzati (ν = 0).
Ascissa (m)
0 0.5 1 1.5 2 2.5 3 3.5 4
0.00E+00
2.00E-02
4.00E-02
6.00E-02
Spostamento (mm)
8.00E-02
1.00E-01
1.20E-01
1.40E-01
1.60E-01
1.80E-01
2 Sudd.
4 Sudd.
8 Sudd.
16 Sudd.
32 Sudd.
64 Sudd.
Figura 5.10: Deformata dell'asse calcolata con il metodo dell'integrazione selettiva (ν = 0).
82

Applicazioni in campo elastico lineare Cap. 4
0.00E+00
Ascissa (m)
0 0.5 1 1.5 2 2.5 3 3.5 4
2.00E-02
4.00E-02
6.00E-02
Spostamento (mm)
8.00E-02
1.00E-01
1.20E-01
1.40E-01
1.60E-01
Selettiva / Incompatibile
Linea Elastica
Completa
1.80E-01
Figura 5.11: Deformata dell'asse calcolata con 16 suddivisiaoni (ν = 0).
0.00E+00
Ascissa (m)
0 0.5 1 1.5 2 2.5 3 3.5 4
2.00E-02
4.00E-02
6.00E-02
Spostamento (mm)
8.00E-02
1.00E-01
1.20E-01
1.40E-01
1.60E-01
Selettiva / Incompatibile
Linea Elastica
Completa
1.80E-01
Figura 5.12: Deformata dell'asse calcolata con 64 suddivisiaoni (ν = 0).
83

Applicazioni in campo elastico lineare Cap. 4
Dalle elaborazioni numeriche eseguite a modulo di Poisson nullo, risulta che la soluzione calcolata
tramite i solidi incompatibili coincide con quella calcolata con l’integrazione selettiva. Si può notare
anche in questo esempio come la velocità di convergenza del solido integrato in modo completo, sia
nettamente inferiore a quella dei solidi che utilizzano metodi che riducono il locking a taglio. Per
ottenere la stessa precisione (in termini di freccia) del modello con 64 suddivisioni e integrazione
completa, è sufficiente utilizzare il modello a 8 suddivisioni con integrazione selettiva.
Dai grafici di fig. 5.11 e 5.12 si nota che con 16 suddivisioni il modello che utilizza l’integrazione
selettiva, o le funzioni di forma non compatibili, si sovrappone in maniera pressoché perfetta alla
deformata teorica derivante dalla linea elastica mentre il modello con l’integrazione completa ne
sottostima gli abbassamenti di circa il 40%. Passando poi al modello con 64 suddivisioni, il calcolo
con l’integrazione selettiva risulta più accurato della stessa teoria di De Saint Venant (che non tiene
conto della deformabilità a taglio).
-1.50
Ascissa (m)
-1.00
2 Sudd.
4 Sudd.
8 Sudd.
16 Sudd.
32 Sudd.
64 Sudd.
Momento (KN m)
-0.50
0.00
0 0.5 1 1.5 2 2.5 3 3.5 4
0.50
1.00
Figura 5.13: Momento flettente dei vari modelli con integrazione selettiva (ν = 0).
Per quanto riguarda le azioni interne, i modelli a integrazione completa o con funzioni non
compatibili, forniscono buoni risultati.
84

Applicazioni in campo elastico lineare Cap. 4
-1.50
Ascissa (m)
-1.00
4 Sudd.
64 Sudd.
De Saint Venant
Momento (KN m)
-0.50
0 0.5 1 1.5 2 2.5 3 3.5 4
0.00
0.50
1.00
Figura 5.14: Confronto con il momento flettente teorico (ν = 0).
2.5
Ascissa (m)
2
1.5
1
0.5
Taglio (KN)
0
0 0.5 1 1.5 2 2.5 3 3.5 4
-0.5
-1
-1.5
De Saint Venant
32 Suddivisioni
-2
-2.5
Figura 5.15: Confronto con il taglio teorico, i pallini indicano il valore del taglio nel baricentro degli elementi.
85

Applicazioni in campo elastico lineare Cap. 4
Per i grafici 14 e 15 vanno aggiunte alcune precisazioni. Il momento è stato calcolato integrando sulla
sezione le tensioni sigma che si ottengono negli 8 punti di Gauss, sia per il modello ad integrazione
selettiva, sia per il modello con le funzioni di forma non compatibili. Il primo infatti utilizza
l’integrazione completa per le tensioni sigma (e ridotta per le tau) mentre il secondo utilizza sempre
l’integrazione completa, ma con 3 funzioni in più. Essendo in modulo di Poisson nullo si ha:
( a + b ⋅ x + c ⋅ y + d ⋅ z + e ⋅ x ⋅ y + f ⋅ y ⋅ z + g ⋅ x ⋅ z + h ⋅ x ⋅ y ⋅ z)
∂
σ x
= E ⋅ε
x
= E ⋅
=
∂x
f ( y,
z)
Per cui la tensione in direzione x, risulta costante, all’interno di un elemento, lungo l’asse X. Essendo
poi nullo anche il modulo di Poisson, lo spostamento in direzione X è costante lungo la larghezza
della trave, per cui sparisce anche la dipendenza dalla coordinata y. Le tensioni calcolata con
l’integrazione selettiva sono risultate identiche a quelle calcolate con il modello con funzioni di forma
incompatibili.
Differente è il discorso per quanto riguarda il taglio. La forza di taglio è stata anch’essa calcolata
integrando le tau sulla sezione ma il modello con integrazione selettiva utilizza le tau calcolate nel
solo baricentro dell’elemento, mentre il modello con le funzioni di forma non compatibili, utilizza le
tau calcolate negli 8 punti di Gauss. I valori delle tau calcolate in questi 8 punti sono risultati identici
al valore della tau calcolata nel baricentro dell’elemento integrato in modo selettivo. Per questi motivi
i grafici 14 e 15 valgono per entrambi i modelli.
Nettamente diversi sono i grafici del momento e del taglio per l’elemento integrato in modo
completo. Se dai grafici 14 e 15 si nota che il valore del momento e del taglio calcolati nel baricentro
(punto dell’integrazione ridotta ovvero punto ottimale per il calcolo delle tensioni), dai grafici 16 e 17
si nota come solo infittendo la suddivisione i diagrammi del momento e del taglio si avvicinino a
quelli teorici. Il diagramma del taglio rimane comunque ben lontano da quello teorico, anche con 64
suddivisioni, solo valore del baricentro, si avvicina all’andamento corretto.
86

Applicazioni in campo elastico lineare Cap. 4
-1.5
Ascissa (m)
-1
De Saint Venant
16 Suddivisioni
64 Suddivisioni
Momento (KN m)
-0.5
0 0.5 1 1.5 2 2.5 3 3.5 4
0
0.5
1
Figura 5.16: Diagramma del momento flettente derivante dal modello con integrazione completa (ν = 0).
6
Ascissa (m)
4
De Saint Venant
64 Suddivisioni
Deformata
2
Taglio (KN)
0
0 0.5 1 1.5 2 2.5 3 3.5 4
-2
-4
-6
-8
-10
Figura 5.17: Diagramma del taglio derivante dal modello con integrazione completa (ν = 0).
87

Applicazioni in campo elastico lineare Cap. 4
2.5
Ascissa (m)
2
1.5
De Saint Venant
64 Suddivisioni
1
Taglio (KN m)
0.5
0
0 0.5 1 1.5 2 2.5 3 3.5 4
-0.5
-1
-1.5
-2
-2.5
Figura 5.18: Valori medi del taglio all'interno degli elementi del modello ad integrazione completa (ν = 0).
E’ interessante notare l’andamento del taglio di figura 5.17 e 5.18. All’interno di ogni elemento la τ
subisce una variazione lineare in X. La pendenza di questa variazione cambia da elemento ad
elemento, e si inverte in corrispondenza dei punti di flesso della deformata. Anche se l’andamento
complessivo del taglio di figura 5.17, non rappresenta l’andamento teorico, i valori medi stimanti nel
baricentro degli elementi si sovrappongono correttamente ai valori teorici. Del tutto diverso è invece
l’andamento del momento flettente di figura 5.16, che coglie l’andamento corretto solo in maniera
qualitativa, ed anche con 64 suddivisioni i valori corretti non vengono raggiunti nemmeno nel
baricentro.
I grafici delle azioni interne riportati in questo capitolo, sono ricavati integrando le rispettive tensioni
(sigma per il momento e τ per il taglio) sulla sezione. Questi grafici possono indurre a credere che
l’equilibrio globale non sia garantito, difatti in figura 5.16 il momento d’incastro è ben lontano dal
valore
2
p ⋅ l
12
necessario per l’equilibrio. Questa differenza è dovuta al fatto che in una soluzione per
elementi finiti, l’equilibrio è garantito solamente in termini di variabili nodali.
88

Applicazioni in campo elastico lineare Cap. 4
Le forze nodali appartenenti ad un elemento si ricavano come:
F
e
n n n
T
∫ B ⋅ ⋅ dV =
Ve
i= 1 j= 1 k = 1
= ∑∑∑
T
[ B ⋅σ
⋅ det( J )] ⋅Wi
⋅W
j
⋅Wk
σ (5.2)
ijk
Per l’elemento ad integrazione completa, per quello ad integrazione selettiva il prodotto matriciale va
eseguito a blocchi, separando i termini taglianti da quelli normali, ed i primi vanno calcolati nel solo
punto centrale. Esaminiamo il caso dell’integrazione completa, la generica forza in direzione X del
nodo m, vale (nel caso in esame si ha solo σ x e τ xz ) :
F
xm
n
n
n
= ∑∑∑
i= 1 j= 1 k = 1
⎡⎛
∂N
m
⎢⎜
⎣⎝
∂x
⋅
∂N
m
σ
x
+ ⋅τ
xz ⎟ ⋅ det( J ) ⋅Wi
⋅W
j
⋅Wk
(5.3)
∂z
⎞
⎠
⎤
⎥
⎦
ijk
La forza nodale in direzione X dipende nel caso esaminato, non solo dalla σ x ma anche dalla τ xz .
Eseguendo il calcolo del momento nella sezione di incastro, tramite le F x il valore
2
p ⋅ l
12
risulta
verificato. Risolvendo la struttura tramite l’integrazione selettiva le σ e le τ assumono valori
differenti, ma l’integrazione tramite la (5.2) fornisce le stesse reazioni vincolari calcolate con
l’integrazione completa. Per le forze in direzione Z (taglio), la (5.2) diviene (sempre nel caso
dell’integrazione completa):
F
zm
n
n
n
= ∑∑∑
i= 1 j= 1 k = 1
⎡⎛
∂N
m
⎢⎜
⎣⎝
∂x
⎞ ⎤
⋅τ xz ⎟ ⋅ det( J ) ⎥ ⋅Wi
⋅W
j
⋅Wk
(5.4)
⎠ ⎦
ijk
Si nota che, per il caso considerato, l’equilibrio in direzione Z è garantito dalla sola tensione τ xz (a
differenza dell’equilibrio in direzione X).
Il diagramma del taglio incrocia il diagramma esatto nel baricentro degli elementi (figure 5.17 e
5.18), questo punto è il punto di integrazione ridotta per l’elemento. Come illustrato in [Malerba] e in
89

Applicazioni in campo elastico lineare Cap. 4
[Barlow] i punti di integrazione ridotta sono particolari punti, detti anche “Optimal Sampling Points”
in cui i valori di sforzo hanno lo stesso grado di accuratezza degli spostamenti nodali.
L’elemento finito è in grado di descrivere in maniera “esatta” un campo di spostamenti con una
variazione lineare, per cui avendo il grafico del taglio una variazione lineare, l’elemento fornisce la
soluzione corretta nei sui “Optimal Sampling Points”, ovvero nel suo baricentro. La tensione σx ha
invece una variazione parabolica lungo X, per cui l’elemento non ne da un valore corretto nemmeno
nei suoi punti di integrazione ridotta, mentre si può notare dalla figura 5.19 che anche con 16
elementi il valore della τ xz nel baricentro degli elementi è corretto.
10
Ascissa (m)
8
6
De Saint Venant
16 Suddivisioni
Deformata
4
2
Taglio (KN)
0
0 0.5 1 1.5 2 2.5 3 3.5 4
-2
-4
-6
-8
-10
Figura 5.19: Diagramma del taglio derivante dal modello con integrazione completa (ν = 0).
Dalle elaborazioni numeriche effettuate risulta che nel caso dell’integrazione selettiva la τ xz calcolata
nel baricentro risulta esatta mentre nel caso si utilizzino le funzioni di forma non compatibili, la τ xz
valutata negli 8 punti di gauss risulta pari al valore dalla τ xy nel baricentro.
90

Applicazioni in campo elastico lineare Cap. 4
Infine tutti i modelli sono stati analizzati considerando un modulo di Poisson pari a 0.2.
1.80E-01
1.60E-01
1.40E-01
1.20E-01
Freccia (mm)
1.00E-01
8.00E-02
6.00E-02
Incompatibile
Selettiva
Completa
Linea Elastica
4.00E-02
2.00E-02
0.00E+00
0 10 20 30 40 50 60
Divisioni in asse
Figura 5.20: Convergenza sulla freccia in mezzeria dei 3 metodi analizzati (ν = 0.2).
Come anche osservato nel caso di una mensola caricata ad un’estremità, la soluzione ottenuta con
l’integrazione selettiva, risulta più rigida di quella ottenuta con le funzioni di forma incompatibili.
Notiamo infine che le soluzioni calcolate con 2 soli elementi lungo l’asse risultano coincidenti per i 3
metodi, sia nel caso con ν = 0 che con ν = 0.2. In questo caso infatti, essendo la suddivisone
esattamente in mezzeria, gli elementi sono soggetti ad uno stato di taglio puro e l’abbassamento
risulterà pari a:
s =
p ⋅ L
8
2
2 ⋅ (1 + ν )
⋅
A ⋅ E
trovati dall’analisi numerica.
che fornisce 0 .003
mm se ν = 0 e 0.004 mm se ν = 0.2 in accordo coi risultati
91

Applicazioni in campo elastico lineare Cap. 4
5. Studio della deformabilità trasversale e dell’ingobbimento sezionale di un
elemento in parete sottile a profilo rettangolare chiuso.
Si fa riferimento ad un elemento incastrato ad una estremità e soggetto ad una coppia torcente
all’estremità opposta, avente un rapporto geometrico tra dimensione minima della sezione e
lunghezza pari ad 1/10. Si studiano diversi casi al variare dei seguenti parametri, α = t/h, β = b/h,
avendo indicato con t lo spessore del profilo e con h e b, rispettivamente la minima e la massima
dimensione trasversale della sezione.
Figura 5.21: Assonometria e sezione trasversale dell'elemento.
La deformabilità trasversale e l’ingobbimento sezionale del profilo vengono quantificati mediante i
parametri D max e I max. Il parametro I max rappresenta il valore massimo dell’ingobbimento presente
nella sezione, mentre D max è la massima differenza tra la posizione di un punto, appartenente alla
sezione in posizione deformata, e la posizione che avrebbe lo stesso punto se la sezione ruotasse
rigidamente.
92

Applicazioni in campo elastico lineare Cap. 4
Rotazione rigida
Figura 5.22: Rappresentazione dei parametri D max e I max .
Si riporta graficamente la variazione di questi parametri al variare di α e β nei seguenti intervalli:
0.025 < α < 0.1 5 cm < t < 20 cm
1 < β < 2 200 cm < b < 400 cm
L’altezza h della sezione (200 cm) e la lunghezza l dell’elemento (2000 cm) vengono mantenuti
costanti in tutte le elaborazioni effettuate. Il materiale utilizzato ha la seguenti caratteristiche
meccaniche: E = 30000 MPa, ν = 0.2, mentre la sollecitazione torcente ha il valore di M t = 1 MNm.
In ultimo si riportano i grafici adimensionalizzati rispetto alla quantità
la rotazione media equivalente della sezione.
h
ϕ ⋅ , dove con ϕ si è indicata
2
93

Applicazioni in campo elastico lineare Cap. 4
Figura 5.23: Rappresentazione in 3D del parametro di rotazione media (rad).
94

Applicazioni in campo elastico lineare Cap. 4
0.006
0.005
Valore parametro di rotazione
0.004
0.003
0.002
0.001
β (b/h)
0.000
0.025 0.030 0.035 0.040 0.045 0.050 0.055 0.060 0.065 0.070 0.075 0.080 0.085 0.090 0.095 0.100
α (t/h)
Figura 5.24: Rotazione media in funzione del parametro α.
0.006
0.005
Valore parametro di rotazione
0.004
0.003
0.002
0.001
α (t/h)
0.000
1 2 3 4 5 6 7 8 9 10 11
β (b/h)
Figura 5.25: Rotazione media in funzione del parametro β.
95

Applicazioni in campo elastico lineare Cap. 4
Figura 5.26: Rappresentazione in 3D del parametro di ingobbimento (rad).
96

Applicazioni in campo elastico lineare Cap. 4
0.006
0.005
β (b/h)
Valore parametro di ingobbimento (cm)
0.004
0.003
0.002
0.001
0.000
0.025 0.030 0.035 0.040 0.045 0.050 0.055 0.060 0.065 0.070 0.075 0.080 0.085 0.090 0.095 0.100
α (t/h)
Figura 5.27: Ingobbimento in funzione del paramentro α.
0.006
0.005
0.004
0.003
0.002
Valore parametro di ingobbimento (cm)
α (t/h)
0.001
0.000
11
10
9
8
7
6
5
4
3
2
1
β (b/h)
Figura 5.28: Ingobbimento in funzione del paramentro β.
97

Applicazioni in campo elastico lineare Cap. 4
Figura 5.29: Rappresentazione in 3D del parametro di rotazione media (rad).
98

Applicazioni in campo elastico lineare Cap. 4
0.020
0.018
0.016
Valore parametro di perdita di forma (cm)
0.014
0.012
0.010
0.008
0.006
β (b/h)
0.004
0.002
0.000
0.025 0.030 0.035 0.040 0.045 0.050 0.055 0.060 0.065 0.070 0.075 0.080 0.085 0.090 0.095 0.100
α (t/h)
Figura 5.29: Perdita di forma in funzione del paramentro α.
0.020
0.018
0.016
Valore parametro di perdita di forma (cm)
0.014
0.012
0.010
0.008
0.006
α (t/h)
0.004
0.002
0.000
1 2 3 4 5 6 7 8 9 10 11
β (b/h)
Figura 5.30: Perdita di forma in funzione del paramentro β.
99

Applicazioni in campo elastico lineare Cap. 4
6. Patch Test per l’elemento solido con acciaio diffuso
Per il solo codice di calcolo operante con l’integrazione selettiva, si esegue un Patch Test a trazione
sulla struttura già analizzata negli esempi 1 e 2 avendo aggiunto dell’armatura diffusa lungo le 3
direzioni cartesiane. Il materiale ipotizzato possiede una E c = 40 MPa, ν = 0.2, E s = 200 MPa, ρ x =
0.1, ρ y = 0.05, ρ z = 0.01. Per semplificare i conti di prova che si eseguono senza l’ausilio del codice
di calcolo, la struttura viene vincolata come in figura 5.31:
z
y
Faccia vincolata in X
Faccia con cedimenti
unitari
x
Faccia vincolata in Y
Faccia vincolata in Z
Figura 5.31: Vincoli assunti.
Rispetto agli esempi 1 e 2 solo le quattro facce indicate risultano vincolate (3 con vincoli fissi ed 1
con cedimenti imposti) e i vincoli sono posti solamente nella direzione dell’asse perpendicolare alla
faccia. Come negli esempi 1 e 2 il cedimento in direzione X è stato imposto unitario e la mesh di 8
elementi risulta distorta dalla posizione del nodo interno.
Per avere dei risultati da confrontare con quelli ottenuti dal codice di calcolo, il problema è stato
risolto tramite il metodo delle forze. Il metodo delle forze permette di scrivere le equazioni risolventi
il problema, dopo aver tolto dei vincoli dalla struttura originaria; le equazioni che si dovranno
scrivere saranno perciò di congruenza. In questo esempio si è scelto di degradare il vincolo a terra in
direzione X, assegnando la reazione R al solido.
100

Applicazioni in campo elastico lineare Cap. 4
Risulta poi necessario degradare i 3 vincoli interni tra il solido e l’armatura, mettendo perciò in
evidenza le 3 reazioni interne esistenti tra il solido e l’armatura: F x , F y , F z . In figura 5.32 si riporta per
semplicità un analogo caso in 2D con cedimento in direzione Y.
Cedimento
R
Cedimento
Fy
R + Fy
Fx
R + Fy
Fx
Fx
Fx
R
Fy
Figura 5.32: Struttura degradata per il caso piano.
Si deve quindi scrivere 4 equazioni di congruenza, la prima tra il solido ed il vincolo a terra, le altre 3
tra il solido e l’armatura diffusa. In queste equazione deve essere tenuta in conto anche la
deformazione per effetto Poisson. Il sistema risolvente è:
⎡ b
⎢ Ec
⋅ Ac
⎢
⎢
⎢
b
⎢ Ec
⋅ Ac
⎢
⎢ ν ⋅ b
⎢−
⎢ Ec
⋅ A
⎢
⎢ ν ⋅ b
⎢
−
⎣ Ec
⋅ A
c
c
⎛
⎜
⎝ E
c
b
⋅ A
b
E ⋅ A
c
c
+
E
ν ⋅ b
−
E ⋅ A
c
ν ⋅ b
−
E ⋅ A
c
c
sx
c
c
b
⋅ A
sx
⎞
⎟
⎠
⎛
⎜
⎝ E
c
ν ⋅ b
−
E ⋅ A
ν ⋅ b
−
E ⋅ A
b
⋅ A
c
c
c
+
E
ν ⋅ b
−
E ⋅ A
c
c
c
sy
c
b
⋅ A
sy
⎞
⎟
⎠
⎛
⎜
⎝ E
c
ν ⋅ b
−
E ⋅ A
ν ⋅ b
−
E ⋅ A
ν ⋅ b
−
E ⋅ A
b
⋅ A
c
c
c
c
+
E
c
c
c
sz
b
⋅ A
sz
⎤
⎥ ⎡ R ⎤ ⎡∆⎤
⎥ ⎢ ⎥ ⎢ ⎥
⎥ ⎢ ⎥ ⎢ ⎥
⎥ ⎢ ⎥ ⎢ ⎥
⎢
Fx
⎥ ⎢
0
⎥ ⎥
⎥ ⋅ ⎢ ⎥ = ⎢ ⎥
⎥ ⎢ ⎥ ⎢ ⎥
⎥ ⎢F
⎥ ⎢ ⎥
y
0
⎥ ⎢ ⎥ ⎢ ⎥
⎥ ⎢ ⎥ ⎢ ⎥
⎞⎥
⎢ ⎥ ⎢ ⎥
⎟
⎥ ⎢⎣
Fz
⎥⎦
⎢⎣
0⎥⎦
⎠⎦
(5.6)
Dove ∆ è il cedimento e b è il lato del cubo. I risultati ottenuti sono: R = 120.8130582 N, F x = -40.0
N, F y = 3.264551894 N, F z = 0.8007391435, che in termini di tensioni nel solido divengono: σ x =
20.203265 MPa, σ y = 0.81613797 MPa, σ z = 0.2001847859 MPa.
101

Applicazioni in campo elastico lineare Cap. 4
I risultati ottenuti col codice di calcolo sono:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
2 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
3 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
4 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
5 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
6 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
7 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
8 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
9 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
mentre lo spostamento del punto centrale (di coordinate 0.2, 0.1, 0.3) risulta:
u = 6.000000000000001E-001
v = -8.977517708654141E-002
w = -1.301201108715740E-001
Lo spostamento esatto del punto centrale è pari a 0.6 mm in direzione X (variazione lineare del
cedimento imposto), mentre per agli altri 2 spostamenti:
ε
y
σ
y ν
= − ⋅ ( σ
x
+ σ
z
) = −0.0816138
E E
c
c
σ
z ν
ε
z
= − ⋅ ( σ
x
+ σ
y
) = −0.100092
E E
c
c
v =
ε y
b
⋅( + 0.1) = −0.0897752
2
w =
ε z
b
⋅( + 0.3) = −0.130120
2
In accordo coi risultati forniti dal codice di calcolo.
102

Applicazioni in campo elastico lineare Cap. 4
7. Patch Test per l’elemento solido con acciaio embedded
Si è ripetuto l’esempio 6 sostituendo all’armatura diffusa delle barre embedded di pari area. Per
semplicità si è scelto di utilizzare la mesh di 8 elementi non distorti ma non simmetrici (il punto
centrale ha coordinate 0.2, 0.1, 0.3). In ogni direzione si sono inserite 4 barre di armatura in modo che
ogni elemento abbia 3 barre embedded al suo interno.
z
y
x
Figura 5.33: Visualizzazione della sola armatura in direzione Y.
Per poter rappresentare un modello analogo all’esempio 6, le barre vengono posizionate in modo che
passino per i baricentri dei singoli elementi finiti. L’area della barra viene calcolata in modo che
rappresenti l’armatura diffusa all’interno del singolo elemento. Ad esempio, le prime nove barre
avranno le seguenti caratteristiche:
Xa Ya Za Xb Yb Zb Es As Eps0 Ele
-1.00 0.55 0.65 0.20 0.55 0.65 200.00 0.0630 0.0 1
-0.40 0.10 0.65 -0.40 1.00 0.65 200.00 0.0420 0.0 1
-0.40 0.55 0.30 -0.40 0.55 1.00 200.00 0.0108 0.0 1
-1.00 -0.45 0.65 0.20 -0.45 0.65 200.00 0.0770 0.0 2
-0.40 -1.00 0.65 -0.40 0.10 0.65 200.00 0.0420 0.0 2
-0.40 -0.45 0.30 -0.40 -0.45 1.00 200.00 0.0132 0.0 2
-1.00 0.55 -0.35 0.20 0.55 -0.35 200.00 0.1170 0.0 3
-0.40 0.10 -0.35 -0.40 1.00 -0.35 200.00 0.0780 0.0 3
-0.40 0.55 -1.00 -0.40 0.55 0.30 200.00 0.0108 0.0 3
103

Applicazioni in campo elastico lineare Cap. 4
I risultati coincidono con quelli calcolati nell’esempio 5, le tensioni nel solido sono:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
2 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
3 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
***
8 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
9 .2020E+02 .8161E+00 .2002E+00 .0000E+00 .0000E+00 .0000E+00
mentre lo spostamento del punto centrale (di coordinate 0.2, 0.1, 0.3) risulta:
u = 6.000000000000002E-001
v = -8.977517708654144E-002
w = -1.301201108715734E-001
e coincide con quello calcolato nell’esempio 6. Infatti anche se le due mesh hanno geometria diversa
a livello dei singoli elementi (l’esempio 6 ha una mesh distorta), il punto centrale ha sempre
coordinate 0.2, 0.1, 0.3.
La struttura è stata poi analizzata ponendo nullo il modulo di Poisson, i risultati trovati sono, in
termini di tensioni:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
2 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
3 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
***
8 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
9 .2000E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
e in termini di spostamento del punto centrale:
u = 6.000000000000014E-001
v = -1.423827492354191E-016
w = 1.484372108007727E-016
L’unica tensione non nulla risulta in direzione X, poiché non essendoci effetto Poisson la congruenza
in direzione Y e Z tra il solido e l’armatura è automaticamente verificata già nella posizione
indeformata. Difatti il punto centrale subisce uno spostamento solo in direzione X in cui avviene il
cedimento imposto.
104

Applicazioni in campo elastico lineare Cap. 4
8. Patch Test per l’elemento solido presollecitato.
Alla struttura dell’esempio 7 vengono tolti i vincoli che impongono il cedimento, e viene inserita una
deformazione iniziale delle armature in direzione X pari al 10%. La precompressione inserita nel
codice di calcolo non tiene conto delle perdite elastiche (verrà infatti usata per rappresentare cavi
post-tesi) e si riduce al calcolo delle forze equivalenti come visto al punto (2.47) :
F
p
= A⋅
E
c
⋅
T T
( N − N ) ⋅T
⋅ε
bi
A
B
z
y
Direzione presollecitata
Faccia vincolata in X
x
Faccia vincolata in Y
Faccia vincolata in Z
Figura 5.34: Rappresentazione della struttura presollecitata.
I risultati in termini di tensioni sono:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
2 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
***
7 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
8 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
9 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
Il calcolo delle tensioni corrette all’interno della struttura può essere eseguito col metodo delle forze,
come visto nell’esempio 5.
105

Applicazioni in campo elastico lineare Cap. 4
Per questo calcolo l’armatura verrà considerata come distribuita, avendo già comprovato
l’equivalenza tra i due modelli analizzati. La forza equivalente di precompressione agente sulle facce
perpendicolari all’asse X, risulta:
Fp = Asx
⋅ Esx
⋅ε
i
= 0 .4 ⋅ 200 ⋅ 0.1 = 8
N
Il sistema risolvente è:
⎡⎛
⎢
⎜
⎢⎝
E
⎢
⎢
⎢
⎢
⎢
⎢⎣
c
b
⋅ A
c
+
E
ν ⋅ b
−
E ⋅ A
c
ν ⋅ b
−
E ⋅ A
c
sx
c
c
b
⋅ A
sx
⎞
⎟
⎠
⎛
⎜
⎝ E
c
ν ⋅ b
−
E ⋅ A
b
⋅ A
c
c
+
E
ν ⋅ b
−
E ⋅ A
c
c
sy
c
b
⋅ A
sy
⎞
⎟
⎠
⎛
⎜
⎝ E
c
ν ⋅ b
−
E ⋅ A
ν ⋅ b
−
E ⋅ A
b
⋅ A
c
c
c
+
E
c
c
sz
b
⋅ A
sz
⎤
⎥ ⎡F
⎥ ⎢
⎥ ⎢
⎥ ⋅ ⎢F
⎥ ⎢
⎞⎥
⎢
⎥ ⎢
⎟ ⎣F
⎠⎥⎦
x
y
z
⎡ b ⋅ Fp
⎤ ⎢
⎥ ⎢
Ec
⋅ Ac
⎥ ⎢ ν ⋅ b ⋅ F
⎥ = ⎢−
⎥ ⎢ Ec
⋅ Ac
⎥ ⎢ ν ⋅ b ⋅ F
⎥
⎦ ⎢−
⎢⎣
Ec
⋅ Ac
p
p
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦
(5.7)
Dove come di consuetudine, si è indicato con Fi la forza scambiata tra armatura e solido in direzione
i. I risultati ottenuti sono: F x = 2.648720302 N, F y = -.2161721220 N, F z = -.5302335068,
che in termini di tensioni nel solido divengono: σ x = -1.337820 MPa, σ y = -0.0540430 MPa, σ z = -
0.132558 MPa. I risultati ottenuti col codice di calcolo sono:
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
2 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
3 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
4 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
5 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
6 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
7 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
8 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
9 -.1338E+01 -.5404E-01 -.1326E-01 .0000E+00 .0000E+00 .0000E+00
Risultano perciò corretti. Non si riporta il controllo sullo spostamento del nodo centrale che
comunque risulta corretto.
106

Applicazioni in campo elastico lineare Cap. 4
9. Pilastro soggetto a peso proprio
Gli stessi modelli utilizzati nell’esempio 3 (vedi la figura 5.3) vengono ora riproposti per lo studio di
un pilastro soggetto al solo peso proprio. Il pilastro è costituito da un solo materiale (senza armature)
avente E = 30.000 MPa, ν = 0.0, γ x = 3750.0 KN / m 3 .
La soluzione del problema è nota dalla teoria dell’elasticità:
x
x = L
d
σ x
x
+ σ ⋅ dx
dx
γ
dx
x = 0
σ x
Figura 5.35: Rappresentazione del problema nella teoria dell'elasticità.
L’equazione differenziale negli spostamenti che regge il problema in esame è:
2
∂ u γ
=
2
∂x
E
(5.8)
Una volta integrata, ed imposto le condizioni al contorno, si hanno:
γ 2
u = ⋅ x
2 ⋅ E
γ ⋅ L
− ⋅ x
E
(5.9)
σ = γ ⋅ ( x − L)
(5.10)
x
107

Applicazioni in campo elastico lineare Cap. 4
Ascissa (m)
0
0 0.5 1 1.5 2 2.5 3 3.5 4
-0.2
Abbassamento (mm)
-0.4
-0.6
-0.8
De Saint Venant
2 Suddivisioni
8 Suddivisioni
-1
-1.2
Figura 5.36: Abbassamento lungo l'asse del pilastro.
Ascissa (m)
0
0 0.5 1 1.5 2 2.5 3 3.5 4
-2
-4
-6
Sigma x (MPa)
-8
-10
-12
De Saint Venant
2 Suddivisioni
8 Suddivisioni
32 Suddivisioni
-14
-16
Figura 5.37: Tensione lungo l'asse del pilastro.
Da notare che per cogliere in maniera ottima la deformata e con un errore massimo del 10% la
tensione, sono sufficienti 8 elementi.
108

Applicazioni in campo elastico lineare Cap. 4
10. Studio di una pila da ponte a profilo misto in campo elastico lineare
Scopo centrale del presente lavoro è lo studio in campo non lineare della risposta di una pila da ponte
binata soggetta ad un carico monotonamente crescente. Dopo aver eseguito vari esempi con lo scopo
di assicurarsi del corretto funzionamento del codice di calcolo implementato, verranno qua riportati
gli studi eseguiti in campo elastico lineare con lo scopo di costruire un adeguato modello in grado di
cogliere il comportamento della struttura.
900
V
V
40
50
40
20
110
60
Asse del ponte
600
820
4250
(32+32) φ18
per parete
(8+8) φ18
per lama
hp
(53+53) φ30
per lama
(2+2) cavi
per lama
46
46
46
46
46
46
45
107.5
Figura 5.38: Geometria della pila binata (misure in cm).
109

Applicazioni in campo elastico lineare Cap. 4
La tipologia della pila da ponte esaminata è di tipo misto (o binata), la pila risulta infatti suddivisa in
due parti:
- una prima parte (nella zona inferiore) costituita da un cassone monocellulare composto
da due pareti principali sagomate, trasversali rispetto all’asse del ponte collegate mutuamente da due
setti arretrati e posizionati all’inizio della sagomatura.
- Una seconda parte (nella zona superiore) costituita da due lame indipendenti collegate
solo in sommità, ottenute come prolungamento delle pareti principali del cassone.
Con riferimento alla figura 5.38 l’estensione relativa al primo tratto di altezza h p viene caratterizzata
tramite il parametro dimensionale α = h p / h, dove h = 42.5 m. Alla base la pila viene considerata
incastrata rigidamente, e non si eseguirà nessuna modellazione della fondazione o del terreno. In
sommità, essa termina con un tratto molto rigido che, di fatto, impone alle due estremità delle lame
gli stessi spostamenti e le stesse rotazioni. La struttura è precompressa tramite una serie di cavi
verticali disposti lungo gli assi di ciascuna delle due lame e lunghi quanto l’intera pila. La forza totale
di precompressione P in ciascuna lama vale 10 MN. L’altezza totale della pila è pari a 42.5 m ed il
carico verticale su ciascuna lama è V = 30 MN. Le caratteristiche geometriche delle sezioni
trasversali e le disposizioni dell’armatura longitudinale vengono mostrate in figura 5.38. Come
armatura trasversale viene considerata una staffatura di 1φ10 ogni 10 cm lungo tutto il profilo della
pila. Per i materiali si considerano le seguenti caratteristiche di base:
Calcestruzzo: f c0 = -33.2 MPa ε c0 = -0.002 ε cu = -0.0035
Acciaio normale: f sy = 430 MPa E s = 210 GPa ε su = -0.01
Acciaio da precompressione: f py = 1600 MPa E p = 200 GPa ε pu = -0.01
Il modulo di rigidità tangente del calcestruzzo viene assunto pari a (Eurocodice 2):
1/ 3
Ec0 = 9500 ⋅ f
c0
= 30533
MPa
110

Applicazioni in campo elastico lineare Cap. 4
Per quanto riguarda il livello di precompressione nei cavi, si assume una tensione a perdite lente
scontate pari a σ p0 = 1000 MPa, mentre le perdite per attrito in rettilineo vengono valutate assumendo
un coefficiente di attrito µ = 0.3 ed una curvatura non intenzionale dei cavi k = 0.0016.
Allo scopo di individuare un adeguata discretizzazione per la pila, in questo paragrafo verrà
analizzata in campo elastico lineare senza armatura, senza precompressione e senza il vincolo sugli
spostamenti relativi della sommità delle lame. Inoltre non viene considerato il carico verticale dovuto
all’azione esercitata dal ponte sovrastante, bensì un carico orizzontale pari a 18 MN su ciascuna lama.
Sotto queste ipotesi la pila si comporta come una mensola di sezione variabile, di cui si può
ragionevolmente conoscere il comportamento tramite la teoria delle travi (De Saint Venant e
Timoshenko). Analizzando più modelli si potrà perciò individuare il grado di discretizzazione. Come
suggerito in [Coc] si può utilizzare come indicatore la tensione alla Von Mises. Questa infatti dipende
dalle tensioni in tutte le direzioni, ed un buon modello deve fornirne una variazione non brusca tra i
vari elementi. Per semplicità in questo lavoro, si esaminerà l’accuratezza della discretizzazione
solamente considerando lo spostamento in sommità della mensola.
Una prima approssimazione dello spostamento di sommità è ottenibile dalla teoria delle travi alla De
Saint Venant:
36 MN 36 MN
21.25 m
36 MN
hp = 21.25 m
765 MNm
Figura 5.39: Schema risolutivo per la teoria delle travi.
Lo spostamento in sommità risulta pari a:
f
3
2
2
3
3
P ⋅ L M ⋅ L M ⋅ L P ⋅ L P ⋅ L
= + + + +
3 ⋅ E ⋅ I 2 ⋅ E ⋅ I E ⋅ I 2 ⋅ E ⋅ I 3 ⋅ E ⋅ I
1
1
1
1
2
111

Applicazioni in campo elastico lineare Cap. 4
Equazione che contempla sia gli spostamenti per flessione sia i moti rigidi della parte superiore
dovuti alla flessione della parte inferiore.
I = 143 m
1
. 2
4
I
2
= 95.
11 m
4
I 1 è il momento d’inerzia della parte inferiore, I 2 è il momento d’inerzia della parte superiore. I
moenti d’inerzia calcolati sono riferiti alla sezione dicretizzata di figura 5.42. Si ottiene una freccia
pari a f = 0.22799 m.
Volendo tenere in conto anche il contributo della deformazione tagliante, si esegue un’analisi col
codice di calcolo TELAIO sviluppato dagli allievi Sgambi e Gomez durante il primo anno alla Scuola
di Specializzazione “F.lli Pesenti”. Il fattore di taglio (1/k) viene assunto pari a (Journal of Applied
Mechanics) :
10 ⋅ (1 + ν ) 5
k = = per la parte superiore.
12 + 11⋅ν
6
k =
(12+
72⋅m+
150⋅m
2
+ 90⋅m
3
10 ⋅(1+
ν ) ⋅(1+
3⋅m)
) + ν⋅(11+
66⋅m+
135⋅m
2
2
+ 90⋅m
3
) + 10⋅n
2
⋅((3+
ν ) ⋅m+
3⋅m
2
= 0.2232
)
dove
m
b⋅t
h ⋅ t
h
= ed
b
b
n= con b = base escluso lo spessore delle pareti, h = altezza. Nei calcoli di k si è
h
posto ν = 0. Risulta:
Senza la deformazione tagliante
Con la deformazione tagliante
f = 0.2240 m
f = 0.2353 m
Questi valori verranno utilizzati per stabilire l’accuratezza del modello discreto adottato per la pila. In
prima analisi vengono analizzati i modelli raffigurati nella pagina seguente.
112

Applicazioni in campo elastico lineare Cap. 4
Figura 5.40: Modelli 1 - 2 - 3.
Figura 5.41: Modelli 4 - 5 - 6.
113

Applicazioni in campo elastico lineare Cap. 4
La sezione viene discretizzata come in figura 5.42. Da notare che si è scelto di non seguire la
sagomatura originale che prevedeva l’introduzione di elementi con una dimensione di 20 cm e di altri
elementi distorti. Questo porterà certamente ad un errore di discretizzazione non facilmente valutabile
in campo non lineare.
450
130
Errore di discretizzazione
80
Vincoli di simmetria
per riflessione
60
600
760
Figura 5.42: Discretizzazione della sezione trasversale (dimensioni in cm).
Risultano però valide le ragioni che hanno portato a tale scelta. L’introduzione di elementi di
dimensione pari a 20 cm (molto inferiore ai 60 cm dell’elemento più piccolo) avrebbe portato o ad
una mesh con un brusco cambio di dimensione (e quindi soluzione poco accurata [Coo]) oppure ad
un infittimento molto spinto della discretizzazione con conseguente richiesta di risorse e tempo
macchina non soddisfacibili.
Da notare infine che in tutti i modelli si è sfruttato il vincolo di simmetria per riflessione, ciò a dato la
possibilità di utilizzare mesh con una discretizzazione spinta lungo l’asse di flessione, senza superare
i 2000 gradi di libertà e con una semibanda pari a 106 (questo per la particolare numerazione adottata,
dipende solo dalla discretizzazione della sezione).
Come si vede dalla curva di convergenza riportata nella pagina successiva, la risposta in campo
lineare è molto buona e già il modello 3 da una freccia pari a quella calcolabile col modello di trave
alla Timoshenko.
114

Applicazioni in campo elastico lineare Cap. 4
0.25
Elementi incompatibili
0.24
0.2363 0.2369
0.2380
0.23
0.2320
0.2351
Timoshenko
0.22
De Saint Venant
0.2286
0.2182
Freccia (m)
0.21
0.2
0.2055
0.19
0.1913
Elementi compatibili
0.18
0.17
0.1659
0.16
0 200 400 600 800 1000 1200 1400 1600
Gradi di Liberta'
Figura 5.43: Curva di convergenza dei modelli 1-6.
L’analisi in campo non lineare richiede una discretizzazione sicuramente più fitta di quella richiesta
per un’analisi lineare. Il danneggiamento della parti di struttura porta all’aumento del gradiente delle
tensioni in altre parti, per cui è bene non utilizzare mesh troppo rade. Un infittimento della mesh può
essere utile in zone particolari come all’incastro della pila o nel punto in cui la sezione diventa binata.
Verranno ulteriormente analizzati i modelli 4 e 6 infittendo la mesh nelle zone sopra citate (entrambi
i modelli sono raffinati aggiungendo 6 piani di coordinate nodali). In particolare verrà costruito un
modello (denominato /tris) che abbia una variazione graduale nell’infittimento della mesh.
Come evidenziano i risultati riportati nelle due pagine seguenti, in campo lineare le differenze tra i
modelli non sono molto accentuate, questo perché si è già ad un risultato sostanzialmente corretto (in
termini di freccia) anche col modello 4 (il modello 6/tris da una differenza del 1% rispetto al modello
4). Anche se il miglioramento risulta quasi inconsistente, il modello con un infittimento graduale
della mesh possiede un comportamento migliore.
115

Applicazioni in campo elastico lineare Cap. 4
Figura 5.44: Modelli 4, 4/bis, 4/tris.
0.238
Mod. 4 / tris
0.2377
0.2375
0.2376
Mod. 4 / bis
Freccia (m)
0.237
0.2365
Mod. 4
0.2363
0.236
0.2355
600 700 800 900 1000 1100 1200
Gradi di Liberta'
Figura 5.45: Convergenza dei modelli 4, 4/bis e 4/tris.
116

Applicazioni in campo elastico lineare Cap. 4
Figura 5.46: Modelli 6, 6/bis e 6/tris.
0.239
0.2385
Mod. 6 / tris
0.2383
0.238
Mod. 6
0.2380
0.2383
Mod. 6 / bis
Freccia (m)
0.2375
0.237
0.2365
1500 1600 1700 1800 1900 2000 2100
Gradi di Liberta'
Figura 5.47: Convergenza dei modelli 6, 6/bis e 6/tris.
117

Applicazioni in campo elastico non lineare Cap. 5
Capitolo 5
Applicazioni in campo elastico non lineare
Indice riassuntivo delle applicazioni riportate
- Prove di compressione monoassiale.
- Dominio di rottura di Kupfer.
- Dominio di rottura di Bresler – Pister.
- Pannello soggetto a stato di sforzo di puro taglio.
- Trave di Bresler - Scordelis.
- Analisi di una pila da ponte a profilo misto in campo non lineare.
Tutte le applicazioni riportate in questo capitolo sono state eseguite con il codice di calcolo operante
con le funzioni di forma non compatibili alla Wilson. Le prove di compressione ed i domini di
Kupfer e di Bresler-Pister sono stati ricavati sia con il legame a danneggiamento isotropo, sia con il
legame ortotropo.
118

Applicazioni in campo elastico non lineare Cap. 5
1. Prove di compressione monoassiale
Le applicazioni degli esempi 1, 2, 3, e 4 vengono eseguite sui modelli geometrici già analizzati nel
capitolo precedente. Per il calcestruzzo si assume un modello geometrico formato da 8 elementi che
assemblati tra loro forniscono un cubo di lato 2. La mesh è distorta in quanto il punto centrale non ha
coordinate 0, 0, 0, ma 0.2, 0.1, 0.3. La struttura viene vincolata come in Figura 5.1:
z
y
Faccia vincolata in X
Faccia con cedimenti
unitari
x
Faccia vincolata in Y
Faccia vincolata in Z
Figura 5.1: Vincoli assunti nella prova di compressione uniassiale.
Avendo vincolato solamente 3 facce in direzione ad esse normali, l’elemento risulta libero di
deformarsi per effetto Poisson. La prova viene effettuata a cedimenti imposti, in modo da cogliere
anche il ramo softening della risposta. In questo esempio si vuole confrontare la risposta del legame a
danneggiamento isotropo proposto con 3 delle curve σ - ε presenti nel Model Code 90 per il
calcestruzzo compresso. I materiali utilizzati sono:
f c = 27 MPa Ec = 28500 MPa ε e = 0.00028 ε m = 0.0022 ε u = 0.0070
f c = 39 MPa Ec = 32216 MPa ε e = 0.00036 ε m = 0.0022 ε u = 0.0060
f c = 48 MPa Ec = 34525 MPa ε e = 0.00042 ε m = 0.0022 ε u = 0.0055
119

Applicazioni in campo elastico non lineare Cap. 5
Il valore di ε e viene ricavato per ogni materiale in base alle sperimentazioni eseguite da [KoN] che
indicarono col valore di σ = 0.3 x f c il valore limite della fase elastica. Il valore di ε m viene mantenuto
pari al 2.2 per mille, essendo questo valore quasi indipendente dal valore della resistenza f c . La
grandezza ε u viene invece modificata per tentativi per cogliere la giusta inclinazione del ramo di
softening del calcestruzzo. I calcestruzzi a più elevata resistenza presentano infatti una pendenza più
accentuata, e delle deformazioni ultime minori.
60
50
Curva Calcolata
Tensione di compressione (MPa)
40
30
20
fc = 27 MPa
fc = 48 MPa
fc = 39 MPa
Curva di
Riferimento
10
0
0 0.001 0.002 0.003 0.004 0.005 0.006
Deformazione di compressione
Figura 5.2: Curve sforzo - deformazione nel caso della compressione uniassiale.
Il modello di danno proposto coglie molto bene il primo tratto della curva (tratto ascendente) ed in
modo sufficientemente approssimato il tratto di softening (tratto discendente). I parametri della legge
di evoluzione del danno verranno tarati sulla base della risposta a compressione, la risposta del
modello ad altri tipi di sollecitazione viene riportata nelle pagine seguenti.
120

Applicazioni in campo elastico non lineare Cap. 5
Per questo primo esempio si riportano inoltre i valori delle tensioni in un passo intermedio, nonché i
valori della variabile di danneggiamento nei vari elementi. Vengono riportati i risultati relativi alla
curva con f c = 48.
Le tensioni al passo 30 (cedimento pari a –0.006) sono (in un generico elemento):
PT G SIGMA X SIGMA Y SIGMA Z TAU XY TAU YZ TAU XZ
1 -.4217E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
2 -.4217E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
***
9 -.4217E+02 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
Mentre il danneggiamento vale:
Elem. 1
Elem. 2
Elem. k
DG1
.593E+00
.593E+00
.593E+00
DG2
.593E+00
.593E+00
.593E+00
DG3
.593E+00
.593E+00
.593E+00
DG4
.593E+00
.593E+00
.593E+00
DG5
.593E+00
.593E+00
.593E+00
DG6
.593E+00
.593E+00
.593E+00
DG7
.593E+00
.593E+00
.593E+00
DG8
.593E+00
.593E+00
.593E+00
DG9
.593E+00
.593E+00
.593E+00
Lo spostamento del nodo centrale, di coordinate 0.2, 0.1, 0.3, vale:
u = -3.600000000000000E-003
v = -1.671559930473855E-016
z = 2.175898210753022E-016
Come è possibile notare dai risultati sopra riportati, il danno è costante in tutti gli elementi, in quanto
la mesh (anche se è distorta) è soggetta ad un campo di spostamenti che provoca una tensione
uniforme in tutti gli elementi. Lo spostamento del nodo centrale non è influenzato dal valore del
danno negli elementi, in quanto questo risulta uniforme. Lo spostamento corretto si può sempre
calcolare come:
1.2
u = 0 .006⋅
= 0.0036
2
121

Applicazioni in campo elastico non lineare Cap. 5
2. Dominio di rottura di Kupfer
In questo esempio si vuole ricostruire il dominio di rottura del calcestruzzo sottoposto ad un campo si
sforzi normali biassiali. La curva di riferimento è quella sperimentale, ottenuta da Kupfer e Gerstle
nel 1973 [KuG]. Le equazioni interpolanti il dominio di rottura sono:
σ
2
= f
tu
= 64 (per il campo trazione – trazione) (5.1)
3 2
0.
⋅ f
cu
σ
2
σ
1
= 1+
0.8⋅
(per il campo trazione – compressione)
f tu
f cu
⎛ σ
1
σ
2
⎜ +
⎝ f
cu
f
cu
2
⎞ σ
1
σ
2
⎟ + + 3.65⋅
⎠ f
cu
f
cu
= 0
(per il campo delle compressioni – compressioni)
Oltre al dominio di rottura si controlleranno anche le curve σ − ε per i casi in cui sono note le curve
sperimentali. L’analisi viene sempre condotta sulla mesh descritta nell’esempio 1 (mesh distorta).
Come leggi costitutive in campo non lineare si utilizza sia il modello a danno isotropo proposto, sia il
legame ortotropo in modo da poter confrontare le soluzioni ottenute coi due legami.
122

Applicazioni in campo elastico non lineare Cap. 5
0.2
σ1 / fcu
0
-1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2
-0.2
-0.4
Calcolato
Sperimentale
-0.6
-0.8
-1
-1.2
2 / fcu
-1.4
Figura 5.3: Confronto tra il dominio di Kupfer ed il dominio di rottura calcolato (Modello a Danno Isotropo)
σ1 / fcu
3
0.2
2
0
-1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2
-0.2
-0.4
Sperimentale
Calcolato
-0.6
1
-0.8
-1
-1.2
σ2 / fcu
-1.4
Figura 5.4 : Confronto tra il dominio di Kupfer ed il dominio di rottura calcolato (Modello a Danno Ortotropo)
123

Applicazioni in campo elastico non lineare Cap. 5
Dai grafici seguenti si può notare che anche la correzione apportata al campo delle compressione –
trazione, nel modello a danno isotropo fornisce risultati ottimi (senza di essa l’errore rispetto alle
curve σ − ε sarebbe del 50 %). I risultati ottenuti tramite il modello ortotropo sono invece più
approssimativi, specialmente nel campo compressione – compressione. Il diagramma risultante è
approssimativamente di tipo quadrato, con gli spigoli smussati nel campo della trazione
compressione. Questo smusso si verifica per l’assunzione del parametro di softening ζ (vedi pag. 58)
che riduce la resistenza a compressione in presenza di trazione in altre direzioni principali.
La figura quadrata del diagramma risultante trova giustificazione nell’ipotesi di avere assunto un
coefficiente di Poisson nullo. In questo esempio le direzioni di carico sono infatti anche direzioni
principali (lungo le direzioni principali si valutano i legami costitutivi) e quindi la matrice di
rotazione risulta unitaria. La risposta lungo la direzione X risulta perciò disaccoppiata dalla risposta
in direzione Y, il problema si riduce a:
⎡σ
x ⎤ ⎡E1
⎢ ⎥
=
⎢
⎢
σ
y
⎥ ⎢
0
⎢⎣
0 ⎥⎦
⎢⎣
0
0
E
0
2
0 ⎤ ⎡ ε
x
⎤
⎢ ⎥
0
⎥
⎥
⋅⎢ε
y ⎥
G⎥⎦
⎢ ⎥
⎣γ
xy ⎦
(5.2)
Le tensioni che forniscono il carico ultimo risulteranno quindi pari a σ = f σ ≥ f nel campo delle
i
c
j
c
bicompressioni (dando luogo alla zona 1 del diagramma di Kupfer, fig. 5.4) e
σ = f σ ≤ f nel
i
t
j
t
campo delle bitrazioni (dando luogo alla zona 2). Ad esempio nel campo delle bicompressioni
risulterà σ = f σ ≥ f in tutti i casi in cui si è scelto un rapporto di carico σ / ≥1
motivo per cui
x
c
y
c
il tratto di diagramma corrispondente risulta retto. La zona 3 delle trazioni compressioni, risulta
divisibile in altre 2 sottozone. Una zona più estesa dove il rapporto tra le tensioni di carico è tale da
far giungere la crisi per σ = f σ ≥ f (tratto orizzontale del diagramma) ed una zona meno estesa
i
t
j
c
x
σ y
dove la crisi risulta con
f / f del
σ
i
= fc
σ
j
≤ ft
. La lunghezza di tali zone dipende dal rapporto
c t
calcestruzzo, in genere assunto pari a 10 o 12 (Il tratto orizzontale è 10 o 12 volte il tratto verticale).
Da notare che il coefficiente di softened introdotto a pag. 59 con lo scopo di abbassare la resistenza a
compressione nel caso fossero presenti delle trazioni trasversali, influisce sulla resistenza ultima
124

Applicazioni in campo elastico non lineare Cap. 5
solamente per il tratto verticale della zona 3 e per un brevissimo tratto orizzontale, causando uno
smusso del diagramma di Kupfer. Per la restante zona 3 difatti, la crisi sopraggiunge sulla
componente a trazione quando la componente di compressione risulta ancora inferiore alla resistenza
massima diminuita dall’effetto softened.
Effetto softened
0.2
σ1 / fcu
0
-1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0
Figura 5.5: Effetto Softened sulla resistenza ultima a compressione trazione.
La zona interessata dall’effetto softened risulterà tanto maggiore quanto il rapporto
f / f si avvicina
c
t
ad 1. Per un calcestruzzo in cui la resistenza a trazione risulta circa un decimo di quella a
compressione, l’effetto softened risulta circoscritto ad una piccola zona del diagramma delle trazioni
compressioni. Si riportano di seguito le curve σ − ε ottenute, sovrapposte a quelle sperimentali. I casi
riportati sono:
- compressione biassiale -1 : -1 : 0
- compressione biassiale -1 : -0.52 : 0
- compressione trazione -1 : 0.102 : 0
- compressione trazione -1 : -0.204 : 0
Si noti che per le ε 2 ed ε 3 nel caso della compressione monoassiale e per la sola ε 3 per il caso della
compressione biassiale, la curva sperimentale presenta quasi un plateau orizzontale che il non si
riesce a cogliere. Ciò è dovuto al fenomeno della dilatanza, ovvero all’aumento della deformazione
trasversale (dovuta al solo effetto Poisson a provino integro) quando ci si avvicina alla resistenza
massima. Il modello ortotropo assume un coefficiente ν post - fessurazione nullo, per cui nei relativi
grafici mancheranno le curve tensione – deformazione dovute all’effetto Poisson.
125

Applicazioni in campo elastico non lineare Cap. 5
1.6
ε1 , ε2
1.4
1.2
Tensione / fcm
ε3
1.0
0.8
Curva Calcolata
Curva di Riferimento
0.6
0.4
0.2
0.0
Deformazione
-4.50E-03 -3.50E-03 -2.50E-03 -1.50E-03 -5.00E-04 5.00E-04 1.50E-03 2.50E-03 3.50E-03 4.50E-03 5.50E-03
Figura 5.6: Compressione biassiale -1 : -1 : 0 (Modello Isotropo).
1.6
ε1
ε2
1.4
1.2
Tensione / fcm
1.0
ε3
0.8
0.6
0.4
Curva Calcolata
Curva di Riferimento
0.2
Deformazione
-4.00E-03 -3.00E-03 -2.00E-03 -1.00E-03 0.00E+00 1.00E-03 2.00E-03
0.0
Figura 5.7: Compressione biassiale -1 : -1 : 0 (Modello Ortotropo).
126

Applicazioni in campo elastico non lineare Cap. 5
1.6
ε1
ε2
1.4
1.2
Tensione / fcm
1.0
ε3
0.8
0.6
0.4
Curva Calcolata
Curva di Riferimento
0.2
Deformazione
-4.00E-03 -3.00E-03 -2.00E-03 -1.00E-03 0.00E+00 1.00E-03 2.00E-03
0.0
Figura 5.8: Compressione biassiale -1 : -0.52 : 0 (Modello Isotropo).
1.6
ε1
ε2
1.4
1.2
Tensione / fcm
1.0
ε3
0.8
0.6
0.4
Curva Calcolata
Curva di Riferimento
0.2
Deformazione
-4.00E-03 -3.00E-03 -2.00E-03 -1.00E-03 0.00E+00 1.00E-03 2.00E-03
0.0
Figura 5.9: Compressione biassiale -1 : -0.52 : 0 (Modello Ortotropo).
127

Applicazioni in campo elastico non lineare Cap. 5
0.7
ε1
Tensione / fcm
0.6
0.5
ε2
ε3
0.4
Curva Calcolata
0.3
Curva di Riferimento
0.2
0.1
Deformazione
-0.002 -0.0015 -0.001 -0.0005 0 0.0005
0
Figura 5.10: Compressione - Trazione -1 : 0.103 : 0 (Modello Isotropo).
0.7
ε1
ε2
Tensione / fcm
0.6
0.5
0.4
ε3
Curva Calcolata
0.3
Curva di Riferimento
0.2
0.1
Deformazione
-0.002 -0.0015 -0.001 -0.0005 0 0.0005
0
Figura 5.11: Compressione - Trazione -1 : 0.103 : 0 (Modello Ortotropo).
128

Applicazioni in campo elastico non lineare Cap. 5
0.4
ε2
ε1
Tensione / fcm
0.35
0.3
0.25
ε3
0.2
Curva Calcolata
Curva di Riferimento
0.15
0.1
0.05
Deformazione
-0.0011 -0.0009 -0.0007 -0.0005 -0.0003 -0.0001 0.0001 0.0003 0.0005
0
Figura 5.12: Compressione - Trazione -1 : 0.202 : 0 (Modello Isotropo).
0.4
ε2
ε1
Tensione / fcm
0.35
0.3
ε3
0.25
0.2
0.15
0.1
Curva Calcolata
0.05
Curva di Riferimento
Deformazione
0
-0.0005 -0.0004 -0.0003 -0.0002 -0.0001 0 0.0001 0.0002 0.0003 0.0004 0.0005
Figura 5.13: Compressione - Trazione -1 : 0.202 : 0 (Modello Ortotropo).
129

Applicazioni in campo elastico non lineare Cap. 5
3. Dominio di rottura di Bresler – Pister.
In questo esempio si vogliono riprodurre i risultati sperimentali ottenuti da Bresler e Pister nel 1958
per il caso di calcestruzzi sottoposti a sforzi di compressione – taglio, trazione – taglio [BrP]. Per
l’esecuzione delle prove sperimentali sono stati utilizzati provini tubolari di diametro esterno di 23
cm, diametro interno di 15 cm e lunghi 76 cm, con 3 diversi valori di resistenza a compressione.
Un’approssimazione del dominio di rottura può essere ottenuta col criterio di Mohr, (o della curva
intrinseca) adatto per i materiali fragili.
(a)
(b)
Figura 14: Cerchi di Mohr. (a) Cerchio (σ 1 -σ 3 ): condizioni di rottura di uno stato di tensione tridimensionale. Cerchio (0-
σ cr ): condizioni di rottura a compressione semplice. Cerchio (σ crt -0): condizioni di rottura di trazione semplice. (b)
Relazione trastato di di sforzo σ-τ e sforzi principali.
Impostando la proporzione B 3 K/B 1 L=B 2 B 3 /B 2 B 1 e sostituendo l’espressione degli sforzi principali, si
ottiene l’espressione analitica della condizione di rottura:
2
1 2 2 2
σ − ( 1−
ρ)
⋅σ
⋅σ
cr
+ ρ⋅(1+
) ⋅τ
= ρ⋅σ
cr
(5.2)
ρ
dove ρ=f ctm /f cm .
130

Applicazioni in campo elastico non lineare Cap. 5
Si riportano si riportano i risultati dell’analisi numerica eseguita sia col modello a danno isotropo sia
col modello a danno ortotropo, il dominio di rottura sperimentale ed il dominio di rottura derivante
dal criterio di Mohr. Si noti che i risultati sperimentali sono compresi tra le due linee tratteggiate. La
difficoltà dell’esecuzione di questo tipo di prova e l’uso di calcestruzzi di diversa resistenza, ha infatti
portato ad una notevole dispersione dei risultati. Il modello a danno fornisce comunque dei buoni
risultati, approssimando molto bene i risultati sperimentali nel campo della compressione – taglio e
sovrastimando leggermente la resistenza nel campo della trazione – taglio. Il modello ortotropo coglie
comunque meglio la forma del dominio di rottura, anche se sovrastima leggermente la resistenza nel
campo del taglio – compressione.
0.300
0.250
Dispersione Sperimentale
Dispersione Sperimentale
Mohr
Modello isotropo
Modello isotropo
τ / fcu
0.200
0.150
0.100
0.050
σ / fcu
0.000
-0.200 0.000 0.200 0.400 0.600 0.800 1.000 1.200
Figura 5.15: Confronto tra i domini di Bresler – Pister ed il dominio di rottura calcolato.
131

Applicazioni in campo elastico non lineare Cap. 5
4. Pannello soggetto a taglio puro
Si vuole riprodurre il comportamento a taglio puro di un pannello in calcestruzzo armato. Il pannello
scelto fa parte di una serie di pannelli testati sperimentalmente da Vecchio, Collins e Melhorn (1985)
per una competizione internazionale sulla predizione della risposta strutturale di pannelli in C.A. Di
seguito si riportano i dati di alcuni dei pannelli testati.
Caratteristiche geometriche dei pannelli [MPa]
Pannello
Sperime
ntazione
angolo
armature
si no α2 [°] ρ
l
Armature
Longitudinali Trasversali
'
ε
f
ly
ρ
t
f
ty
Calcestruzzo
PV10 X 90 0.0179 276 0.0100 276 0.00270 14.5
PV11 X 90 0.0179 235 0.0131 235 0.00260 15.6
PV12 X 90 0.0179 469 0.0045 269 0.00250 16.0
PV18 X 90 0.0179 431 0.0032 412 0.00220 19.5
PV19 X 90 0.0179 458 0.0071 299 0.00220 19.0
PV20 X 90 0.0179 460 0.0089 297 0.0018 19.6
c
'
f
c
Caratteristiche del materiale (E s = 200000 MPa) [MPa]
Pannello
E
Teoria MCFT
Teoria STM
' '
'
c
= 2 f c
/ ε
c f
cr
= 0.33
f
c
'
E
c
= 3875 f
c
PV10 10740.7 1.26 14755.6 1.18
PV11 12000.0 1.30 15305.0 1.22
PV12 12800.0 1.32 15500.0 1.24
PV18 17727..3 1.46 17111.5 1.37
PV19 17272.7 1.44 16890.7 1.35
PV20 21777.8 1.46 17155.4 1.37
f =
cr
'
0.31
f
c
Si è scelto di testare il solo pannello PV19, confrontando i risultati ottenuti sia con i risultati
sperimentali, sia con i risultati ottenuti dall’ing. Gomez utilizzando le stesse leggi costitutive
(ortotrope) assunte in questo lavoro, con un codice di calcolo non ad Elementi Finiti.
132

Applicazioni in campo elastico non lineare Cap. 5
Si noti la perfetta corrispondenza con i risultati ottenuti dall’ing. Gomez, nonché la buona
approssimazione ai risultati reali.
4.5
4
Sperimentale
3.5
3
Tesi ing. Gomez
Tensione τ (MPa)
2.5
2
Tesi ing. Sgambi (modello ortotropo)
1.5
1
0.5
0
0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01
Deformazione γ
Figura 5.15: Curva γ - τ per il pannello PV19.
L’utilizzo di un legame isotropo porterebbe in questo caso ad una resistenza ultima pari alla
resistenza di fessurazione, con una tensione nulla nelle barre di armatura. Un modello isotropo non è
quindi in grado di rappresentare il comportamento di una membrana in calcestruzzo armato quando
siano presenti sforzi di taglio rilevanti. Questo appare chiaro se consideriamo il sistema che governa
la risposta del modello isotropo in caso di stato di sforzo piano di taglio puro:
⎡ 0 ⎤ ⎡D
⎢ ⎥
=
⎢
⎢ 0 ⎥ ⎢
D
⎢ ⎥
⎣τ
⎦
⎢
xy ⎣ 0
11
21
D
D
12
0
22
0 ⎤ ⎡ ε
x
⎤
⎢ ⎥
0
⎥
⎥
⋅(1−
d)
⋅⎢ε
y ⎥
D ⎥⎦
⎢ ⎥
33 ⎣γ
xy ⎦
(5.3)
dove d indica il danneggiamento del materiale.
133

Applicazioni in campo elastico non lineare Cap. 5
La matrice di rigidità del materiale possiede sempre la forma data nella 5.3, con degli zeri in
posizione (1,3) (2,3) (3,1) e (3,2) che provocano il disaccoppiamento delle equazioni che governano
la risposta a taglio da quelle che governano la risposta alle azioni normali. Si hanno perciò i seguenti
2 sistemi:
⎡0⎤
⎡
⎥ = D
⎢ ⎢
⎣0⎦
⎣D
11
21
D
D
21
22
⎤ ⎡ ⎤
⎥ ⋅ ε
x
(1−
d)
⋅⎢
⎥
⎦ ⎣ε
y ⎦
(sistema che governa la risposta ad azioni normali) (5.4)
τ = D33 ⋅(1−
d)
⋅γ
(sistema che governa la risposta ad azioni di taglio) (5.5)
xy
xy
dato che la matrice di rigidità presente nella (5.4) possiede rango 2 (se così non fosse sarebbe il
modulo E del calcestruzzo pari a 0) il sistema (5.4) ammette come unica soluzione la soluzione nulla
x
=
y
ε 0 ε =0 con conseguente errato inutilizzo delle armature poste in direzione X e Y.
La risposta strutturale risulta perciò governata dalla sola equazione (5.5) che fornisce come resistenza
ultima del pannello, la resistenza a taglio del solo calcestruzzo.
Col modello ortotropo, nel momento in cui la matrice diagonale delle rigidità nel sistema di
riferimento principale viene ruotata nel sistema di riferimento X,Y si trova un sistema con matrice dei
coefficienti piena e di rango 3 (altrimenti si avrebbe una direzione i in cui E i = 0 ma questo è escluso
dalle leggi costitutive anche nel caso di trazione pura):
⎡ 0 ⎤ ⎡D11
D12
D13
⎤ ⎡ ε
x
⎤
⎢ ⎥ ⎢
⎥ ⎢ ⎥
⎢ 0 ⎥=
⎢
D21
D22
D23
⎥
⋅⎢ε
y ⎥
⎢ ⎥ ⎢⎣
⎥⎦
⎢ ⎥
⎣τ xy ⎦ D31
D32
D33
⎣γ
xy ⎦
(5.6)
essendo i coefficienti in posizione (1,3) (2,3) (3,1) e (3,2) non più nulli, una deformazione a taglio
provoca anche delle deformazioni in direzione X e Y che chiamano in causa le relative armature (se
presenti). Nasceranno quindi delle tensioni di tipo σ in direzioni X e Y, tuttavia le tensioni σ presenti
nel calcestruzzo saranno equilibrate dagli sforzi presenti nell’armatura (se la membrana è soggetta a
taglio puro le tensioni σ che nascono sono autoequilibrate all’interno della struttura).
134

Applicazioni in campo elastico non lineare Cap. 5
5. Trave di Bresler – Scordelis
Si considera come primo esempio, due delle travi provate sperimentalmente da Bresler e Scordelis
nel 1961, e precisamente la trave A-1 e la trave OA-1. La trave A-1 è caratterizzata da una forte
armatura flessionale e da una debole armatura a taglio, in modo da raggiungere un collasso con un
meccanismo di parete. La trave OA-1, rispetto alla A-1, è del tutto sprovvista di armatura trasversale
e di armatura al positivo. In fig. 5.16 sono riportate le dimensioni, le disposizioni di armatura e le
caratteristiche dei materiali della trave A-1. La struttura è stata suddivisa in 297 elementi finiti, per un
totale di 2040 gradi di libertà. Tuttavia, essendo la struttura sottoposta ad uno stato di sforzo piano, i
gradi di libertà che effettivamente concorrono a rappresentare il modello sono solo 680. Tutte le
armature presenti sono state assegnate in modo diffuso, il carico di prova e le reazioni vincolari sono
state ripartite nell’intorno del punto di applicazione, per evitare arbitrarie concentrazioni di sforzo.
Figura 5.16: Geometria della trave di Bresler Scordelis con staffatura.
135

Applicazioni in campo elastico non lineare Cap. 5
500
450
400
350
Carico applicato (KN)
300
250
200
150
Risultati sperimentali
Elaborazione numerica
100
50
0
0 2 4 6 8 10 12 14 16
Freccia massima (mm)
Figura 5.17: Curva carico freccia, sperimentale e calcolato.
L’elaborazione numerica con un legame costitutivo ortotropo fornisce una buona interpretazione del
comportamento strutturale della trave. Nelle pagine seguenti vengono riportate le immagini di
fessurazione ricavate numericamente, da confrontare con il quadro fessurativo sperimentale riportato
in fig. 5.18.
Figura 5.18: Quadro fessurativo sperimentale sulle 2 facce della trave armata a taglio.
136

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.19: Quadro fessurativo al 10% del carico ultimo.
Figura 5.20: Quadro fessurativo al 40% del carico ultimo.
137

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.21: Quadro fessurativo al 80% del carico ultimo.
Figura 5.22: Quadro fessurativo al 100% del carico ultimo.
138

Applicazioni in campo elastico non lineare Cap. 5
400
350
300
Carico applicato (KN)
250
200
150
Sperimentale
elaborazione numerica
100
50
0
0 1 2 3 4 5 6 7 8
Freccia massima (mm)
Figura 5.23: Curva carico freccia, sperimentale e calcolato.
Nelle pagine seguenti vengono riportate le immagini di fessurazione ricavate
numericamente, da confrontare con il quadro fessurativo sperimentale riportato in figura
5.24.
Figura 5.24: Quadro fessurativo sperimentale sulle 2 facce della trave armata a taglio.
139

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.25: Quadro fessurativo al 15% del carico ultimo.
Figura 5.26: Quadro fessurativo al 40% del carico ultimo.
140

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.27: Quadro fessurativo al 80% del carico ultimo.
Figura 5.28: Quadro fessurativo al 100% del carico ultimo.
141

Applicazioni in campo elastico non lineare Cap. 5
6. Analisi di una pila da ponte binata
Si riprende la pila da ponte studiata in campo elastico lineare e riportata nel capitolo precedente a
pag. 112. Per comodità si riportano le caratteristiche geometriche e meccaniche della pila.
La tipologia della pila è di tipo misto (o binata), la pila risulta infatti suddivisa in due zone:
900
V
V
40
50
40
20
110
60
Asse del ponte
600
820
4250
(32+32) φ18
per parete
(8+8) φ18
per lama
hp
(53+53) φ30
per lama
(2+2) cavi
per lama
46
46
46
46
46
46
45
107.5
Figura 5.29: Geometria della pila binata (misure in cm).
una prima parte (nella zona inferiore) costituita da un cassone monocellulare composto da due pareti
principali sagomate, trasversali rispetto all’asse del ponte collegate mutuamente da due setti arretrati
e posizionati all’inizio della sagomatura ed una seconda parte (nella zona superiore) costituita da due
lame indipendenti collegate solo in sommità, ottenute come prolungamento delle pareti principali del
cassone.
142

Applicazioni in campo elastico non lineare Cap. 5
Con riferimento alla Figura 5.29 l’estensione relativa al primo tratto di altezza h p viene caratterizzata
tramite il parametro dimensionale α = h p / h, dove h = 42.5 m. Alla base la pila viene considerata
incastrata rigidamente, e non si eseguirà nessuna modellazione della fondazione o del terreno. In
sommità, essa termina con un tratto molto rigido che, di fatto, impone alle due estremità delle lame
gli stessi spostamenti e le stesse rotazioni. L’altezza totale della pila è pari a 42.5 m ed il carico
verticale su ciascuna lama è V = 30 MN. Le caratteristiche geometriche delle sezioni trasversali e le
disposizioni dell’armatura longitudinale vengono mostrate in figura 5.29. Come armatura trasversale
viene considerata una staffatura di 1φ10 ogni 10 cm lungo tutto il profilo della pila. Per i materiali si
considerano le seguenti caratteristiche di base:
Calcestruzzo: f c0 = -33.2 MPa ε c0 = -0.002 ε cu = -0.0035
Acciaio normale: f sy = 430 MPa E s = 210 GPa ε su = -0.01
Acciaio da precompressione: f py = 1600 MPa E p = 200 GPa ε pu = -0.01
Il modulo di rigidità tangente del calcestruzzo viene assunto pari a (Eurocodice 2):
1/ 3
0 0
=
Ec = 9500 ⋅ f
c
30533
MPa
L’analisi numerica prevede di sottoporre la pila ad un carico orizzontale crescente in sommità, sino al
raggiungimento del carico massimo. La pila è stata analizzata in entrambe le direzioni di inflessione
di fig. 5.30:
Figura 5.30: Direzione di flessione 1 e 2.
143

Applicazioni in campo elastico non lineare Cap. 5
Durante la flessione nella direzione 1, il comportamento strutturale è quello di tipo trave. Una
aumento dell’altezza della costolatura aumenta la resistenza a flessione della struttura.
14
12
10
Forza orizzontale (MN)
8
6
4
Parametro α
crescente
2
0
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40
Spostamento in sommità (m)
Figura 5.31: Curve forza spostamento per flessione in direzione 1.
Le curve rimangono comunque pressoché simili, in quanto il comportamento globale della struttura
non subisce grandi alterazioni rispetto a quello originario, l’incremento di resistenza dovuto
all’aumento dell’altezza della costolatura è modesto. Il comportamento è sostanzialmente di tipo
trave, a parte una piccola zona diffusiva al termine della costolatura per i casi di α = 1/3 e α = 2/3.
Più interessante sono i risultati per una flessione in direzione 2. Anche in questa direzione la pila può
essere pensata come composta da due travi, ma la parte superiore (senza costolatura) possiede una
deformabilità notevolmente superiore rispetto alla parte inferiore a cassone. L’incremento di
resistenza all’aumentare dell’altezza della costolatura è notevole, e ad un incremento di capacità
portante corrisponde un relativo decremento di deformabilità. La pila senza costolatura risulta quindi
essere la più deformabile ma la meno portante (riferito ad una forza orizzontale in sommità), mentre
la pila con sezione uniforme a cassone è la struttura più portante ma meno deformabile.
Dal punto di vista computazionale, il modelli utilizzati per l’analisi della flessione in direzione hanno
144
Parametro α
crescente

Applicazioni in campo elastico non lineare Cap. 5
richiesto una mesh di circa 5000 gradi di libertà (contro i circa 2500 nel caso di flessione in direzione
1). Nel grafico riportato in Figura 5.32 vengono evidenziate anche le stesse curve ricavate dall’ing.
Biondini nella sua Tesi di Dottorato [Bio] con elementi di tipo trave.
18
16
14
Analisi con elementi di trave
Analisi con elementi solidi
12
Forza orizzontale (MN)
10
8
6
4
2
0
0 0.2 0.4 0.6 0.8 1 1.2
Spostamento in sommità (m)
Figura 5.32: Curve forza spostamento per flessione in direzione 2.
Si noti l’estrema corrispondenza tra la risposta calcolata con elementi di tipo trave e quella con
elementi finiti solidi, nei casi della prima e della quarta curva (pila senza costolatura, pila con
costolatura completa). Nel caso di una costolatura non completa, l’elemento di tipo trave non coglie
in modo sufficientemente corretto la deformabilità dell’elemento, causando delle sovrastime anche
del 20% sulla resistenza ultima. L’errore si incrementerà maggiormente col diminuire della snellezza
della pila stessa. Nelle pagine successive si riportano tutti i casi studiati, con le relative curve carico
spostamento ed i loro quadri fessurativi.
145

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 1 con costolatura nulla (α=0)
Figura 5.33: Mesh indeformata, e visione assonometrica della deformata.
12
10
8
Forza orizzontale (MN)
6
4
Asse del ponte
2
0
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40
Spostamento in sommità (m)
Figura 5.34: Risposta in termini di carico orizzontale - freccia.
146

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.35: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.36: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
147

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 1 con costolatura ad 1/3 dell’altezza totale (α=1/3)
Figura 5.37: Mesh indeformata, e visione assonometrica della deformata.
14
12
10
Forza orizzontale (MN)
8
6
Asse del ponte
4
2
0
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40
Spostamento in sommità (m)
Figura 5.38: Risposta in termini di carico orizzontale - freccia.
148

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.39: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.40: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
149

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 1 con costolatura ad 2/3 dell’altezza totale (α=2/3)
Figura 41: Mesh indeformata, e visione assonometrica della deformata.
14.00
12.00
10.00
8.00
6.00
Asse del ponte
4.00
2.00
0.00
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40
Figura 5.42: Risposta in termini di carico orizzontale - freccia.
150

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.43: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.44: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
151

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 1 con costolatura ad 3/3 dell’altezza totale (α=3/3)
Figura 5.45: Mesh indeformata, e visione assonometrica della deformata.
14.00
12.00
10.00
Forza orizzontale (MN)
8.00
6.00
Asse del ponte
4.00
2.00
0.00
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40
Spostamento in sommità (m)
Figura 5.46: Risposta in termini di carico orizzontale - freccia.
152

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.47: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.48: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
153

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 2 con costolatura ad 0/3 dell’altezza totale (α=0)
Figura 5.49: Mesh indeformata, e visione assonometrica della deformata.
5
4
Forza orizzontale (MN)
3
2
Asse del ponte
1
0
0 0.2 0.4 0.6 0.8 1 1.2
Spostamento in sommità (m)
Figura 5.50: Risposta in termini di carico orizzontale - freccia.
154

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.51: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.52: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
155

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 2 con costolatura ad 1/3 dell’altezza totale (α=1/3)
Figura 5.53: Mesh indeformata, e visione assonometrica della deformata.
6
5
4
Forza orizzontale (MN)
3
2
Asse del ponte
1
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Spostamento in sommità (m)
Figura 5.54: Risposta in termini di carico orizzontale - freccia.
156

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.55: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.56: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
157

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 2 con costolatura ad 2/3 dell’altezza totale (α=2/3)
Figura 5.57: Mesh indeformata, e visione assonometrica della deformata.
12
10
8
Forza orizzontale (MN)
6
4
Asse del ponte
2
0
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Spostamento in sommità (m)
Figura 5.58: Risposta in termini di carico orizzontale - freccia.
158

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.59: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.60: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
159

Applicazioni in campo elastico non lineare Cap. 5
Pila inflessa in direzione 2 con costolatura ad 3/3 dell’altezza totale (α=3/3)
Figura 5.61: Mesh indeformata, e visione assonometrica della deformata.
18
16
14
12
Forza orizzontale (MN)
10
8
6
Asse del ponte
4
2
0
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Spostamento in sommità (m)
Figura 5.62: Risposta in termini di carico orizzontale - freccia.
160

Applicazioni in campo elastico non lineare Cap. 5
Figura 5.63: Quadro fessurativo e danneggiamento per la vista dal lato A. Situazioni al 50%, 75% e 100% del carico
ultimo.
Figura 5.64: Quadro fessurativo e danneggiamento per la vista dal lato B. Situazioni al 50%, 75% e 100% del carico
ultimo.
161

Codici di calcolo sviluppati
App. A
Appendice A
Codici di calcolo sviluppati
All’interno del mio lavoro di tesi ho sviluppato una serie di codici di calcolo in linguaggio Microsoft
Visual Fortran. In questo capitolo se ne da un elenco ed una breve descrizione.
Indice dei codici di calcolo sviluppati
PreCass
PreC
PrePila
Esa3D
CalcEsa
PostEsa2D
Modellatore per una trave con profilo a cassone
Modellatore per una trave con profilo a C
Modellatore per un pila da ponte binata
Programma di grafica 3D
Programma di calcolo non lineare
Post Processor 2D
164

Codici di calcolo sviluppati
App. A
1. PrePila
I codici PreCass, PreC, e PrePila sono molto simili, per cui verrà fornita una descrizione del solo
codice Prepila. Il compito di questo programma è quello di costruire il modello di calcolo di una pila
da ponte ponte binata, dovrà perciò fornire come output le coordinate dei nodi e la matrice delle
incidenze del calcestruzzo, nonché le coordinate nodali e la matrice delle incidenze dell’acciaio
embedded.
LeggiDati
FormaCoordPn1
FormaCoord1
FormaCoordPn2
FormaCoord2
FormaInc1
FormaIncTran
FormaInc2
OrdinaPiani
CalcCoeff
CalcInter
CalcInter
Stampa
Figura A.1: Schema a blocchi del codice PrePila.
Nelle pagine seguenti si riporta un esempio di file di dati, un esempio di pila disegnata in 2D (non
corrisponde a quella del file di dati) e l’output del programma Esa3d.
165

Codici di calcolo sviluppati
App. A
File di DATI di PrePila per la costruzione del modello di pila binata
COSTOLA
4 : File di coordinate
10.0
20.0
40.0
50.0
LAMA
7 : File di coordinate
10.0
20.0
30.0
40.0
50.0
70.0
80.0
SPIGOLI
5.0
10.0
: DY, DZ dei 4 spigoli
ALTEZZA UNITE
4 : File di coordinate
10.0
60.0
120.0
150.0
ALTEZZA SEPARATE
4 : File di coordinate
150.0
190.0
200.0
230.0
EMBEDDING
: X1,Y1,Z1 X2,Y2,Z2
2
10.0 15.0 15.0 230.0 15.0 15.0
10.0 14.0 14.0 230.0 14.0 14.0
Il programma consente un infittimento della mesh in zone dove è intuitiva la presenza di un forte
gradiente di sforzi, ad esempio nei punti in cui la pila da profilo a cassone diventa a doppia lama.
166

Codici di calcolo sviluppati
App. A
Coordinate Lama Coordinate Lama
Coordinate Costola
Coordinate Lama
∆Z
∆Y
Figura A.2: Geometria 2D di una pila da ponte binata.
167

Codici di calcolo sviluppati
App. A
Figura A.3: La mesh creata da PrePila e visualizzata da Esa3D.
FormaCoordPn1
Calcola le coordinate nodali appartenenti al piano perpendicolare all’asse della pila, nella zona di
profilo a cassone.
FormaCood1
Estende le coordinate nodali piane a tutta l’altezza del profilo a cassone.
FormaCoordPn2
Calcola le coordinate nodali appartenenti al piano perpendicolare all’asse della pila, nella zona di
profilo a doppia lama.
168

Codici di calcolo sviluppati
App. A
FormaCood1
Estende le coordinate nodali piane a tutta l’altezza del profilo a doppia lama.
FormaInc1
Forma la matrice delle incidenze per gli elementi esaedrici nella zona di profilo a cassone.
FormaIncTran
Forma la matrice delle incidenze per gli elementi esaedrici nella zona di transizione dal profilo a
cassone al profilo a doppia lama.
FormaInc1
Forma la matrice delle incidenze per gli elementi esaedrici nella zona di profilo a doppia lama.
OrdinaPiani
Forma un array contenente le incidenze di tutte le facce di tutti gli esaedri (6 facce per ogni elemento
finito).
CalcCoeff
Calcola i coefficienti angolari di tutti i piani rappresentanti le facce degli elementi (ordinati nella
subroutine OrdinaPiani) e di tutte le rette rappresentanti gli elementi embedded.
CalcInter
Calcola l’intersezione tra una retta (elemento embedded) e tutti i piani presenti.
ControllaInt
Controlla se l’intersezione calcolata da CalcInter è interna ai nodi appartenenti a quella faccia, se così
è si è trovata una coordinata dell’elemento embedded.
Stampa
Stampa i risultati: matrice delle coordinate e delle incidenze degli esaedri, matrice delle coordinate e
delle incidenze degli elementi embedded.
169

Codici di calcolo sviluppati
App. A
2. Esa3D
Il codice Esa3D visualizza sullo schermo la geometria della struttura. Come dati riceve le coordinate
nodali, le incidenze e la posizione dell’osservatore (punto di osservazione). La visualizzazione sullo
schermo della geometria del solido viene eseguita dopo una serie di calcoli geometrici che
permettono di proiettare il solido su di un piano (piano di disegno). Fissato un punto all’interno del
corpo (punto osservato) il solido viene proiettato su di un piano perpendicolare alla linea
congiungente il punto di osservazione ed il punto osservato, tramite una rotazione del sistema di
riferimento vengono poi calcolate le coordinate delle proiezioni dei nodi sul piano di disegno
(coordinate in 2D) nonché tutte le distanze nodo – proiezione. Basandosi poi sulla liste dei piani che
formano le facce del solido, sulla lista delle rette che formano gli spigoli del solido, e sulle distanze
prima calcolate, vengono cancellati i tratti di linee che sono coperti da parti solide (cancellazione
delle linee nascoste) ed infine viene eseguito il disegno del solido sullo schermo.
LeggiDati
Legge la geometria della struttura e il punto di osservazione.
Medio
Calcola un punto medio all’interno della struttura e lo assume come punto osservato.
OrdinaPiani
Forma un array contenente le incidenze di tutte le facce di tutti gli esaedri (6 facce per ogni elemento
finito).
OrdinaPiani
Forma un array contenente le incidenze degli spigoli di tutti gli esaedri (12 spigolo per ogni elemento
finito).
Piano Pro
Calcola le equazioni di tutte le rette di proiezione.
170

Codici di calcolo sviluppati
App. A
LeggiDati
Medio
OrdinaPiani
OrdinaRette
PianoPro
PianoRetta
Portaa2D
CalCoeff
DistaPro
Estremi
ScalaXY
Disegna
DisegnaLinea
Coperto
Figura A.4: Schema a blocchi del codice Esa3D.
PianoRetta
Calcola le intersezioni tra le rette ed il piano di proiezione.
Portaa2D
Calcola le coordinate nel riferimento locale del piano di proiezione.
Dista
Calcola le distanze dei nodi dal piano di proiezione.
Disegna
Disegna la geometria della struttura, linea per linea, controllando che lo spigolo non sia coperto da
parti solide.
171

Codici di calcolo sviluppati
App. A
Figura A.5: Test di prova per la cancellazione delle linee nascoste.
Figura A.6: Profilo a C discretizzato in Elementi Finiti.
172

Codici di calcolo sviluppati
App. A
Figura A.7: Trave a C discretizzata in Elementi Finiti.
Figura A.8: Trave a cassone discretizzata in Elementi Finiti.
173

Codici di calcolo sviluppati
App. A
3. CalcEsa
In questo lavoro si sono implementati 3 programmi di calcolo ad elementi finiti (operanti
rispettivamente con funzioni di forma compatibili, incompatibili, e con integrazione selettiva). In
questo paragrafo si da una breve descrizione del codice di calcolo operante con le funzioni
incompatibili alla Wilson.
LeggiDati
Legge la geometria della struttura, i vincoli, le forze, i passi di carico e i dati necessari ad effettuare le
proiezioni ortogonali della struttura fessurata. Un esempio di file di dati è il seguente:
File ESA.PRE:
Problema di prova
Dati gen, NCoord NEle NFVar NFCost NVinc NMol NDefI NEmb NDIF NPG NPassi Toll
1482 900 66 66 376 0 0 0 900 8 400 0.01
Coordinate cartesiane, Coordinata X Coordinata Y Coordinata Z
0.000000000000000E+000 0.000000000000000E+000 0.000000000000000E+000
*** *** ***
41.500000000000000 3.800000000000000 9.000000000000000
Incidenze, N1 N2 N3 N4 N5 N6 N7 N8
2 1 7 8 56 55 61 62
*** *** *** *** *** *** *** ***
3 2 8 9 57 56 62 63
Materiale calcestruzzo, FC1 EPS_C1 Fx Fy Fz
31.5D0 -0.002D0 -0.025D0 0.0D0 0.0D0
Forze concentrate variabili, Nodo Fx Fy Fz
1417 0.0 0.0 1.515151515152E-03
*** *** *** ***
1482 0.0 0.0 1.515151515152E-03
Forze concentrate costanti, nodo Fx Fy Fz
1417 -4.5454545454545E-01 0.0 0.0
*** *** *** ***
1482 -4.5454545454545E-01 0.0 0.0
174

Codici di calcolo sviluppati
App. A
Vincoli rigidi, NGDL Flag (1-Fisso 2-Cedimento) Cedimento
1 1 0.0
*** *** ***
4445 1 0.0
Vincoli elastici concentrati, NNodo T1 T2 T3 Rig
Deformazioni iniziali
Elementi Embedding incidenze, NEmbedding per elemento
EE car.,XA YA ZA XB YB ZB EYoung Area DefIniz Ele
Elementi Diffusi, RoX RoY RoZ E FX FY FZ
1.10E-02 3.00E-03 3.00E-03 2.10E+05 4.30E+02 4.30E+02 4.30E+02
*** *** *** *** *** *** ***
1.10E-02 3.00E-03 3.00E-03 2.10E+05 4.30E+02 4.30E+02 4.30E+02
Storia di carico, Moltiplicatore
1.00000E+00
***
1.30500E+02
mentre per eseguire le proiezioni ortogonali della struttura fessurata, si richiede in input anche il
file MINCRIS.PRE:
0 1 0
0 0 0
******
0 0 0
0 0 0
0 1 0
Ogni riga rappresenta un elementi finito. Se nella prima colonna vi è 1 significa che l’elemento
appartiene alla proiezione ortogonale sul piano XY, sul piano XZ se è nella seconda colonna, sul
piano YZ se è nella terza colonna. Di questi elementi verranno stampati le matrici delle incidenze
proiettate in 2 dimensioni, nonché le proiezioni delle inclinazioni di fessurazione.
Semibanda
Calcola la semibanda del sistema risolvente analizzando la matrice delle incidenze.
175

Codici di calcolo sviluppati
App. A
Gauss_non_locale
In ogni punto di Gauss forma un array con i punti che si dovranno considerare per il calcolo delle
deformazioni in senso non locale. Associa inoltre ad ogni punto il relativo peso.
Forma_der_X
Forma la matrice delle derivate delle funzioni di forma rispetto al sistema di riferimento generale (x,
y, z). Al suo interno contiene altre subroutine per il calcolo delle derivate rispetto al sistema di
riferimento standard (ξ,η,ρ), per il calcolo della matrice Jacobiana e del suo determinante, e per la
risoluzione del sistema 3x3 che fornisce le derivate cercate.
Standard_steel
Calcola le coordinate nel sistema di riferimento standard delle intersezioni degli elementi embedded
con le facce degli elementi finiti. Utilizza un algoritmo di Newton per la risoluzione del problema
non lineare della trasformazione di coordinate.
Assembla
Forma la matrice di rigidezza della struttura in forma di semibanda raddrizzata. Al suo interno
contiene altre subroutine per il calcolo della matrice di rigidezza del singolo elemento, per il calcolo
della matrice di rigidezza degli elementi embedded e per la condensazione statica dei gradi di libertà
non compatibili.
Cedim
Impone i vincoli ed i cedimenti.
SBGauss
Risolve il sistema lineare con il metodo di gauss. Contiene delle subroutine per il calcolo del residuo
e per un eventuale raffinamento iterativo della soluzione.
Defo_loc
Calcola le deformazioni in senso locale per ogni elemento finito.
176

Codici di calcolo sviluppati
App. A
Defo_non_loc
Calcola le deformazioni in senso non locale per ogni elemento finito e le sostituisce a quelle locali.
Aggiorna moduli
Esegue il calcolo dei moduli di elasticità danneggiati e della relativa matrice di rigidità del materiale.
Contiene al suo interno le subroutine per il calcolo degli autovalori e degli autovettori con il metodo
di Jacobi, per la valutazione dei legami costitutivi, per la formazione della matrice di rotazione e per
il calcolo della matrice di rigidità nel sistema di riferimento globale (x, y, z).
Stress
Calcola le tensioni nei materiali.
Squilibrio
Calcola il vettore delle forze nodali interne ed il relativo vettore dello squilibrio (differenza tra forze
nodali esterne e forze nodali interne).
Convergenza
Decide se le iterazioni in campo non lineare sono giunte a convergenza.
Stampa_ris
Stampa i risultati dell’elaborazione in termini di: curva forza - spostamento in un punto della
struttura, spostamenti, forze nodali interne e squilibrio in tutti i punti della struttura, tensioni e
deformazioni in tutti i punti di gauss, proiezioni ortogonali dei piani di fessurazione negli elementi
desiderati.
177

Codici di calcolo sviluppati
App. A
LeggiDati
Inizializza
Semibanda
Gauss_non_locale
Incrementa carico
Sino a convergenza
Forma_der_X
Standard_steel
Aggiorna_FNE
Assembla
Cedim
SBGauss
Per ogni elemento:
Forma_der_csi
Forma_Jacobiano
Calcola_der_X
Per ogni elemento:
Forma_K_loc
Forma_K_embedded
Condensa_K
Assembla_K_loc
Defo_loc
Defo_non_loc
Aggiorna_moduli
Stress
Squilibrio
Per ogni elemento:
Calcola_autovalori
Calcola_D123
Forma_T
Calcola_DXYZ
Convergenza
Stampa_ris
Fine elaborazione
Figura A.9: Schema a blocchi del codice CalcEsa.
178

Codici di calcolo sviluppati
App. A
4. PostEsa2D
Disegna a video le proiezioni ortogonali della struttura, con il relativo quadro fessurativo.
LeggiDati
Leggi_inclinazioni
Dis_mesh
Cicla 2 o 3 volte
a seconda dei dati
Dis_fessure
Leggi_danno
Dis_mesh
Cicla 2 o 3 volte
a seconda dei dati
Dis_danno
Stop
Figura A.10: Schema a blocchi del codice PostEsa2D.
I dati per il disegno delle proiezioni ortogonali vengono stampati dal codice CalcEsa. La subroutine
Dis_danno colora le proiezioni degli elementi finiti a seconda del valore dell’indice di fessurazione
posseduto da quell’elemento. Come indice di fessurazione si è assunta la media delle deformazioni
principali in trazione eseguita sui punti di Gauss dell’elemento. La colorazione cambia da chiaro a
scuro a seconda della gravità della fessurazione. Nella pagina successiva si riportano 2 esempi di
post-processing.
179

Codici di calcolo sviluppati
App. A
Figura A.11: Quadro fessurativo e danno nella trave di Bresler Scordelis.
Figura A.12: Indice di danno in una pila binata sottoposta a flessione.
180

Bibliografia
App. B
Appendice B Bibliografia
Libri sulla modellazione numerica e sulle tematiche strutturali
(L1)
(L2)
(L3)
(L4)
Introduzione al metodo degli elementi finiti
Francesco Cesari – Pitagora Editrice Bologna
Problemi non lineari nella meccanica del continuo
Francesco Cesari – Pitagora Editrice Bologna
Codici di calcolo per l’analisi di strutture spaziali
Francesco cesari – Pitagora Editrice Bologna
Analisi per elementi finiti: Modellazione strutturale e controllo dei risultati
Autori Vari – Cism
(L5) The Finite Element Method – Vol 1
Zienkiewicz, Taylor – McGraw Hill
(L6) The Finite Element Method – Vol 2
Zienkiewicz, Taylor – McGraw Hill
(L7)
(L8)
(L9)
(L10)
(L11)
(L12)
Fondamenti del metodo degli elementi finiti
Brebbia, Connor – CittàStudiEdizioni
Programming the finite element method
Smith, Griffiths – Wiley
Finite Element Procedures
Klaus, Bathe – Prentice Hall
Modellistica Numerica per Problemi Differenziali
Quarteroni – Sprinter
Matematica Numerica
Quarteroni, Sacco, Saleri – Sprinter
Analisi numerica
Comincioli – McGraw Hill
(L13) Meccanica delle strutture – Vol 1,
Corradi – McGraw Hill
181

Bibliografia
App. B
(L14) Meccanica delle strutture – Vol 2
Corradi – McGraw Hill
(L15) Meccanica delle strutture – Vol 3
Corradi – McGraw Hill
(L16)
(L17)
The finite element method
Thomas J. R. Hughes
Non linear finite elements for continua and structures
Belytschko, Kam liu, Moran - Wiley
(L18) Non linear finite element analysis of solid and structures – Vol 1
Crisfield – Wiley
(L19)
(L20)
(L21)
(L22)
Non linear finite element analysis of solid and structures – Vol 2Advanced Topics
Crisfield – Wiley
Meccanica dei materiali
Vergani – McGraw Hill
Equazioni differenziali alle derivate parziali
Prouse – Masson
Unified theory of reinforced concrete
Hsu – CRC Press
Articoli e tesi
[Bal]
[Bar]
[BeH]
[BiB]
[Bio]
Balan – Filippou – Popov, Costitutive model for 3D cyclic analysis of concrete structures,
Journal of engineering mechanics, 1997
Barbini, Analisi elastoplastica di strutture in regime “plan strain” e di “plan stress”, Tesi
di laurea, 1987
Belarbi - Hsu, Costitutive laws of softened concrete in biaxial tension-compression, ACI
Journal, 1995
Biondini – Bontempi – Malerba – Martinez y Cabrera, Analisi non lineare di pile da ponte
a doppia lama, Giornate AICAP99
Biondini, Strutture da ponte soggette ad azioni di tipo sismico. Modellazione ed
ottimizzazione, Tesi di dottorato, 2000.
182

Bibliografia
App. B
[BoM1] Bontempi - Malerba, Il controllo della formulazione tangente per la soluzione di problemi
strutturali non lineari, Studi e ricerche 17, 1996
[BoM2] Bontempi - Malerba, The role of softening in the numerical analysis of R.C. framed
structures, Structural Engineering and Mechanics, Vol 5 1997
[BMR1] Bontempi – Malerba – L. Romano, Formulazione diretta secante dell’analisi non lineare di
telai in C. A. e C. A. P. Studi e ricerche 16, 1994
[BMR2] Bontempi – Malerba – L. Romano, Il modello MCFT nell’analisi per elementi finiti di
strutture piane in C.A.. Studi e ricerche 16, 1994
[Cer]
[Cek1]
[Cek2]
[Cek3]
[Cic]
[Col1]
[CoS]
[CoS]
[DaG]
[DaP1]
[DaP2]
[DeA]
Cervera, Simulaciòn numérica de patologìas en presas de hormigon, Technical Report
CINME, 1991
Cervenka – Gerstle, Inelastic analysis of reinforced concrete panels: Theory, IABSE
Pubblications, vol. 31 1971
Cervenka – Gerstle, Inelastic analysis of reinforced concrete panels: experimental,
verification and application, IABSE Pubblications, vol. 32 1972
Cervenka – Pukl, Computer models of concrete structures, Structural Engineering
International, vol. 2/92 1992
Ciccone, Formulazione secante e formulazione tangente nell’analisi non lineare delle
strutture intelaiate in C.A. e C.A.P., Tesi di specializzazione, 1994
Collins – Stevens – Uzmeri – Will, Costitutive model for reinforced concrete finite element
analysis, ACI Structural Journal, 1991
Colombi – Sgambi, Non linear finite element analysis of bone-cement interface condition
in cemented total hip replacement, Engineering Transactions, vol. 47, 1999
Colombi – Sgambi, Non linear finite element analysis of a cemented interface: the bonecement
interface in HIP replacements, Studi e Ricerche, 1999
Danzo – F. Grimoldi, Analisi per elementi finiti di elementi strutturali in C.A. con il
modello di N. S. Ottosen (M.C.90), Tesi di Laurea, 1998
Darwin – Pecknold, Analysis of RC shear panels under cyclic loading, Journal of the
structural Division, 1976
Darwin – Pecknold, Non linear biaxial stress-strain law for concrete, Journal of the
Engineering Mechanics Division, 1977
De Amicis, Elementi in C.A. in regime membranale. Teorie, confronti e apllicazioni, Tesi
di Laurea, 2000
183

Bibliografia
App. B
[Elw]
[Kwa]
[Kon]
[KuG]
[Les]
[LOD]
[Mai]
[Maz]
[MaC]
[PeM]
[Riz]
[Sga]
[SiJ1]
[SiJ2]
[Tay]
[TaS]
Elwi – Murray, A 3D hipoelastic concrete costitutive relationship, Journal of the
Engineering Mechanics Division, 1979
Kwak, Improved numerical approach for the bond-slip behavior under cyclic loads,
Structural Engineering and Mechanics, 1997
Konke, Damage evolution in ductile materials: from micro - to macro damage,
Computational Mechanics 15, 1996
Kupfer – Gerstle, Behavior of concrete under biaxial stresses, J. of the Engineering
Mechanics Division, 1973
On the convergence of Wilson’s Non-conforming Element for Solving the Elastic Problem,
Computer Methods in Applied Mechanics and Engineering, 7 (1976)
Luccioni – Oller – Danesi, Coupled plastic-damaged model, Computer Methods in Applied
Mechanics and Engineering, 1996
Maier, Dispense del corso di Meccanica dei Materiali e della Frattura
Mazars, A description of micro- and macroscale damage of concrete structures,
Engineering Fracture Mechanics, Vol. 25 1986
J. Mazars – G. P. Cabot, Continuum damage theory. Application to concrete. J. of
Engineering Mechanics, 1989
M. A. Perego, Danneggiamento dei materiali lapidei: leggi costitutive, analisi per elementi
finiti ed applicazioni, Tesi di Laurea, 1990
Rizzi, Fracture-energy-based regularization of a scalar damage model, Politecnico di
milano, DIS
Sgambi, Danneggiamento, plasticità e microstruttura nell’analisi del comportamento
meccanico del tessuto osseo spongioso, Tesi di Laurea, 1998
J. C. Simo – J. W. Ju, Strain and stress-based continuum damage models 1) Formulation,
Int. J. Solids Structures, Vol 23 1987
J. C. Simo – J. W. Ju, Strain and stress-based continuum damage models 2) Computational
aspects, Int. J. Solids Structures, Vol 23 1987
Taylor, A Nonconforming Element for Stress Analysis, International Journal for Numerical
Methods in Engineering, 10, no. 6 (1976)
Taylor – Simo – Zienkiewicz - Chan, The Patch Test: a condition for assessing finite
element convergence, International Journal for Numerical Methods in Engineering,1984
184

Bibliografia
App. B
[Val]
[Vec1]
[Vec2]
[Vec3]
Valliappan – Doolan, Non linear analysis of reinforced concrete, ASCE Journal of
Structural Division, vol. 98, ST4
Vecchio – Collins, Predicting the response of reinforced concrete beams subjected to shear
using modified compression field theory, ACI structural journal, 1988
Vecchio, Non linear finite element analysis of reinforced concrete membranes, ACI
Structural Journal, 1989
Vecchio, Reinforced concrete membranes element formulations, ASCE Journal of
Structural division, vol. 16 no. 3
[VMW] Valliappan – Murti – Wohua, Finite element analysis of anisotropic damage mechanics
problems, Engineering Fracture Mechanics, 1990
[VYK]
[Wan]
[Wil1]
[Wil2]
[Wil3]
[Wil4]
[WuH]
[ZhB]
Valliappan – Yazdchi – Khalili, Earthquake analysis of gravity dams based on damage
mechanics concept, International Journal for Numerical and Analytical Methods in
Geomechanics, 1996
Wang – Teng – Cheong Fan, Softened damage model for finite element analysis of
structural concrete deep beams, ACI structural journal, 2001
Wilson et alt., Incompatible Displacement Models, Numerical and Computer Models in
Structural Mechanics, Academic Press, pag 47-57
Wilson - Ibrahimbegovic., Use of incompatible displacement modes for the calculation of
element stiffnesses or stresses, Finite Elements in Analysis and Design, 1990
Wilson, The static condensation algorithm, International Journal for Numerical Methods in
Engineering,1974
Wilson, Sap80 Structural Analysis Program for small or large computer system, CEPA fall
Conference, 1980
Wu – Huang - Pian, Consistency condition and convergence criteria of incompatible
elements: General formulation of incompatible functions and its applications, Journal of
Computer Structure, 1987
Zhefeng – Breyesse, Three-dimensional non linear analysis of reinforced concrete beams,
Engineering Computation, 1991
185