- Page 1:
The Design of Modern Steel Bridges
- Page 5 and 6:
The Design of Modern Steel Bridges
- Page 7 and 8:
Contents Preface vii Acknowledgemen
- Page 9 and 10:
Preface Bridges are great symbols o
- Page 11:
Acknowledgements The figures in Cha
- Page 14 and 15:
2 The Design of Modern Steel Bridge
- Page 16 and 17:
4 The Design of Modern Steel Bridge
- Page 18 and 19:
6 The Design of Modern Steel Bridge
- Page 20 and 21:
8 The Design of Modern Steel Bridge
- Page 22 and 23:
10 The Design of Modern Steel Bridg
- Page 24 and 25:
12 The Design of Modern Steel Bridg
- Page 26 and 27:
14 The Design of Modern Steel Bridg
- Page 28 and 29:
16 The Design of Modern Steel Bridg
- Page 30 and 31:
18 The Design of Modern Steel Bridg
- Page 32 and 33:
20 The Design of Modern Steel Bridg
- Page 34 and 35:
22 The Design of Modern Steel Bridg
- Page 36 and 37:
24 The Design of Modern Steel Bridg
- Page 38 and 39:
26 The Design of Modern Steel Bridg
- Page 40 and 41:
28 The Design of Modern Steel Bridg
- Page 42 and 43:
30 The Design of Modern Steel Bridg
- Page 44 and 45:
32 The Design of Modern Steel Bridg
- Page 46 and 47:
34 The Design of Modern Steel Bridg
- Page 48 and 49:
36 The Design of Modern Steel Bridg
- Page 50 and 51:
38 The Design of Modern Steel Bridg
- Page 52 and 53:
40 The Design of Modern Steel Bridg
- Page 54 and 55:
42 The Design of Modern Steel Bridg
- Page 56 and 57:
44 The Design of Modern Steel Bridg
- Page 58 and 59:
Table 2.1 Properties of some commer
- Page 60 and 61:
48 The Design of Modern Steel Bridg
- Page 63 and 64:
Chapter 3 Loads on Bridges 3.1 Dead
- Page 65 and 66: 3.3 Design live loads in different
- Page 67 and 68: interstate highways are designed fo
- Page 69 and 70: a coefficient that depends on the n
- Page 71 and 72: Loads on Bridges 59 In Germany, a n
- Page 73 and 74: Table 3.6 Typical values of U and P
- Page 75 and 76: 3.5 Longitudinal forces on bridges
- Page 77 and 78: wind loading on the traffic. An upl
- Page 79 and 80: where r is the air density ¼ 1.226
- Page 81 and 82: Loads on Bridges 69 minimum and max
- Page 83 and 84: 3.8 Other loads on bridges There ar
- Page 85 and 86: References Loads on Bridges 73 wher
- Page 87 and 88: Chapter 4 Aims of Design 4.1 Limit
- Page 89 and 90: critical components of the structur
- Page 91 and 92: But this is an attempt to achieve u
- Page 93 and 94: If the basic variables R and S are
- Page 95 and 96: educed variables defined by oi ¼ x
- Page 97 and 98: will have a probability of failure
- Page 99 and 100: Aims of Design 87 g m ¼ g m1 g m2
- Page 101 and 102: Table 4.2 Failure probabilities of
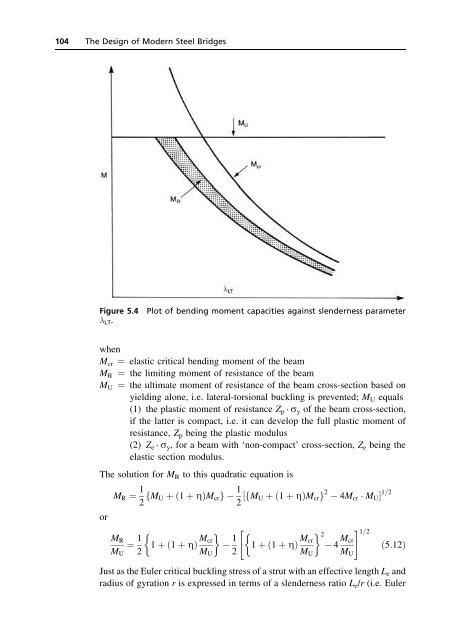
- Page 103 and 104: Chapter 5 Rolled Beam and Plate Gir
- Page 105 and 106: as possible. But deep and thin webs
- Page 107 and 108: eam, with an effective area equal t
- Page 109 and 110: and stresses caused by lateral defl
- Page 111 and 112: Figure 5.3 Beam cross-section. In t
- Page 113 and 114: Rolled Beam and Plate Girder Design
- Page 115: Table 5.2 Effective length factors
- Page 119 and 120: equation (5.16) has been adopted fo
- Page 121 and 122: The strain energy of the elastic re
- Page 123 and 124: Figure 5.6 Buckling of plates in co
- Page 125 and 126: Figure 5.8 Buckling of plate under
- Page 127 and 128: techniques. It may be noted that th
- Page 129 and 130: Rolled Beam and Plate Girder Design
- Page 131 and 132: Rolled Beam and Plate Girder Design
- Page 133 and 134: 5.4.3 Effect of residual stresses R
- Page 135 and 136: Aw ¼ 40 mm 2 , allowing for a smal
- Page 137 and 138: Rolled Beam and Plate Girder Design
- Page 139 and 140: Rolled Beam and Plate Girder Design
- Page 141 and 142: Basler and Thurlimann were the firs
- Page 143 and 144: Ostapenko/Chern gave the following
- Page 145 and 146: where m ¼ Mp b 2 twsyw ty ¼ syw p
- Page 147 and 148: the case of equal flanges, the tota
- Page 149 and 150: emains flat until an elastic critic
- Page 151 and 152: Rolled Beam and Plate Girder Design
- Page 153 and 154: longitudinal compression is given b
- Page 155 and 156: where Peq ¼ s1tB PE Ps Pcro Peq1
- Page 157 and 158: Figure 5.27 Tension-field forces in
- Page 159 and 160: 5.5.6 Design of longitudinal web st
- Page 161 and 162: when Le is the effective length for
- Page 163 and 164: pffiffiffiffiffiffiffiffiffiffiffif
- Page 165 and 166: een derived as a condition for trea
- Page 167 and 168:
For interaction of various stress c
- Page 169 and 170:
must be at least i.e. 1 IsxbB 4 2 a
- Page 171 and 172:
Chapter 6 Stiffened Compression Fla
- Page 173 and 174:
Stiffened Compression Flanges of Bo
- Page 175 and 176:
cross-section in which the secant s
- Page 177 and 178:
longitudinal compression of the lon
- Page 179 and 180:
webs of main girders is denoted by
- Page 181 and 182:
Stiffened Compression Flanges of Bo
- Page 183 and 184:
wherefrom Ms ¼ 2 3 PE P The net be
- Page 185 and 186:
Stiffened Compression Flanges of Bo
- Page 187 and 188:
Stiffened Compression Flanges of Bo
- Page 189 and 190:
Stiffened Compression Flanges of Bo
- Page 191 and 192:
Stiffened Compression Flanges of Bo
- Page 193 and 194:
Stiffened Compression Flanges of Bo
- Page 195 and 196:
Chapter 7 Cable-stayed Bridges 7.1
- Page 197 and 198:
Cable-stayed Bridges 185 cables con
- Page 199 and 200:
The following is a list of cable-st
- Page 201 and 202:
(a) Fan system (b) Harp system (c)
- Page 203 and 204:
7.3.2 Ropes causing lateral compres
- Page 205 and 206:
The spiral winding of wires around
- Page 207 and 208:
polyethylene or even steel tube. Or
- Page 209 and 210:
See Fig. 7.7. Imagine a cable-stay
- Page 211 and 212:
It may be noted that: Et is higher
- Page 213:
Reference Cable-stayed Bridges 201
- Page 216 and 217:
204 The Design of Modern Steel Brid
- Page 218 and 219:
206 The Design of Modern Steel Brid