Abstracts - KTH Mechanics

114
Three-dimensional stability of non-uniform vortex patches
D. Guimbard ∗ , S. Leblanc ∗
The three-dimensional stability of a family of two-dimensional inviscid vortex
patches discovered by Abrashkin & Yakubovich 1 is explored. Generally unsteady
and non-uniform, these vortex patches evolve freely in surrounding irrotational flows.
The family of solutions they discovered are exact solutions of Euler’s equation described
in Lagrangian representation and their corresponding complex trajectories
are:
Z(t) =X(t)+iY (t) =G(ξ)e i(ω+Ω)t + H( ¯ ξ)e iΩt
where G and H are analytic functions, ω and Ω are real numbers.
Described in Lagrangian representation (ξ is the complex lagrangian variable), this
family of solutions includes Rankine circular vortex, Kirchhoff’s ellipse, and freely
rotating multipolar vortices with hypocycloidal shape as special cases and weirdly
Gerstner’s waves.
Taking advantage of their Lagrangian description, the stability analysis is carried
out with the local theory of short wavelength instabilities.
It is shown that, except Rankine vortex, these flows are generically unstable to
three-dimensional disturbances. However, additional effects such as external rotation
or density stratification may be stabilizing 2 .
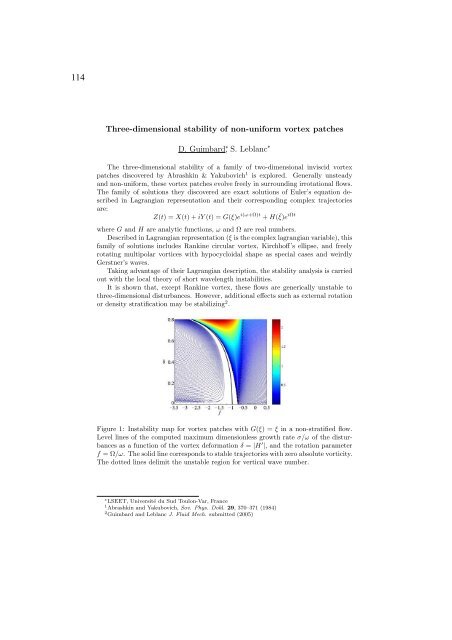
Figure 1: Instability map for vortex patches with G(ξ) =ξ in a non-stratified flow.
Level lines of the computed maximum dimensionless growth rate σ/ω of the disturbances
as a function of the vortex deformation δ = |H ′ |, and the rotation parameter
f =Ω/ω. The solid line corresponds to stable trajectories with zero absolute vorticity.
The dotted lines delimit the unstable region for vertical wave number.
∗ LSEET, Université du Sud Toulon-Var, France
1 Abrashkin and Yakubovich, Sov. Phys. Dokl. 29, 370–371 (1984)
2 Guimbard and Leblanc J. Fluid Mech. submitted (2005)